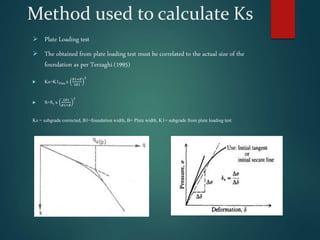
This document discusses the modulus of subgrade reaction (Ks), which represents the relationship between applied stress and associated soil settlement beneath foundations. It defines Ks and describes several analytical models and methods for calculating Ks values, including plate loading tests, correlations with soil properties, and pseudo-coupled approaches that assign different Ks values depending on location beneath the foundation. Factors that influence Ks include soil type, moisture content, and foundation geometry.

1. Modulus of
Subgrade Reaction
PRESENTER:
ABDELRAHMAN ESSAM
S.M ASCE

2. Main
Points
 Definition
 Method of calculations Ks values
 Different analytical Models
 Factors affecting Modulus
 Conclusion

3. Definition
 The structural engineers need an appropriate way to
represent the soil in the structural analysis. Subgrade
reaction modulus (Ks) can be considered as an
appropriate interface between the geotechnical and
structural engineers, Modulus of subgrade reaction in
relationship between applied stress and associated
settlement.
Ks=
𝑃
𝑤
Where P applied stress at foundation level , w associated settlement

4. Definition
 Traditional Design method of shallow foundation (Rigid beam method) is applicable if
foundation act as a rigid foundation that is satisfy the following procedures :
As per Meyerhof relative stiffness factor Kr=
𝐸𝑚𝑑3
12𝐸𝑠𝐵3
Em= young’s modulus of mat foundation , d= depth of mat , Es =young’s modulus of
soil , B=width of mat foundation
Footing consider to be rigid if Kr > 0.5
 If Kr < 0.5 the foundation is considered to be flexible so (Rigid beam method) is
not applicable in this case so foundation should be design as beam on elastic
foundation method (subgrade modulus approach)
Rigid Beam Method Beam on elastic foundation

5. Definition
 Winkler 1867 firstly introduce the model of subgrade
reaction which simulate the soil as group of linear ,
independent springs which not transmit any shear stress
to adjacent springs

6. Method used to calculate Ks
 Methods can be summarized as follow :
1- Plate loading Test
2- Practical relationships
3- Correlation between soil parameters & Tests data
4- Tables
5- Exact way (Calculation of actual stress and actual
associated settlement)

7. Method used to calculate Ks
 Plate Loading test
 The obtained from plate loading test must be correlated to the actual size of the
foundation as per Terzaghi (1995)
 Ks=K1Plate x
𝐵1+𝐵
2𝐵1
2
 S=S1 x
2𝐵1
𝐵1+𝐵
2
Ks = subgrade corrected, B1=foundation width, B= Plate width, K1= subgrade from plate loading test

8. Method used to calculate Ks
 Practical Relationships
 Ks=
0.95 𝐸𝑠
(1−𝜐𝑠2)
𝐵4 𝐸𝑠
1−𝜐𝑠2 𝐸𝐼
0.108
Biot
Where Es=modulus of elasticity of the soil; υs=Poisson’s ratio of the soil; B=beam width and EI=
bending rigidity of the beam
Ks=
0.65 𝐸𝑠
(1−𝜐𝑠2)
12 𝐵4 𝐸𝑠
𝐸𝐼
Vesic
Ks=
𝐸𝑠
𝐵𝐼𝑠 𝐼𝐹 (1−𝜐2)
Bowles (1996)
Where Is= an influence factor that depends on L/B and H/B ; If = an influence factor that depends
on L/B and D/B ; B= the width of the loaded area (beam width);L=the length of the loaded area
(beam length); H= thickness of soil layer =5B as recommended by Bowels, 1996 ; D= foundation
depth .the influence factors of Is and If can be determined from tables prepared by Bowles
(1996).

9. Method used to calculate Ks
 Correlation between soil tests
 There is a lot of Codes that used SPT test to correlate the value between N and
Ks value .
 Also there are correlations between CBR test and Ks value
 Also there are correlations between oedometer test and Ks value

10. Method used to calculate Ks
 Tables

11. Analytical Models
Pseudo-coupled approaches
 Shortcoming of Winkler It considers that springs has the same value in all point
of the mat foundation which not give contact pressure as in reality as shown in
figure the coupling effect became so important especially at edge of mat
foundation ignoring coupling effects leads to underestimation of mat differential
settlements and maximum bending moment. Therefore, a lot of researchers
provided alternative approaches to overcome the above shortcomings Like
Pseudo-Coupled approach.
Contact Pressure under foundation as per continuum theory

12. Analytical Models
Pseudo-coupled approaches
 Pseudo-coupled approach used the same concept of Winkler but
with different values of Ks depending on the location of spring.
Taking larger value near the edge of the foundation compared to its
center

13. Analytical Models
 Coduto proposed a simpler version of pseudo-coupled method Ks under mat
foundation can be estimated as follow
1- using the principle of estimation an initial constant value of Ks average
2- diving mat in N (two or more) concentric zones with central zone having half width and
the length of the mat as shown in figure
3- Ks increase from inner zone to outer zone , Ks for the outer zone should be twice as the
inner zone
4- if A1 (central area), A2(intermediate area) and A3 (outer area)
So Ks1 = Ks aver
𝐴1+𝐴2+𝐴3
𝐴1+1.5𝐴2+2𝐴3
Ks for A1 = Ks1 , Ks for A2 = 1.5 Ks1 and Ks for A3 = 2 Ks1

14. Analytical Models
 Banavalkar and Ulrich developed updated version of pseud-coupled approach called discrete area method
based on ACI concept Ks under mat foundation can be calculation using the following procedure:
1- Estimating uniform value of Ks considering building rested on rigid foundation by using Boussunesq and
Westergarrd theories to estimate the value of settlement under building load.
2- Carry static analysis of mat foundation using the uniform value of Ks initial to get the distribution of the contact
pressure
3- after carrying static analysis the contact pressure under mat foundation divided into rectangular area which
contact pressure could be consider constant.
4- using Boussinesq and Westergaard theories (incase of uniform and layered soil profiles, respectively) to estimate
the settlement under each discrete area of contact pressure to calculate new Ks1
5- using Ks1 to perform static analysis of mat foundation, comparing the resulting deformation with the calculated
value of settlement based (geotechnical theory) if they still far making another iteration by dividing new contact
stress over settlement calculate from Boussunesq then making static analysis again until the values of settlement
became so close