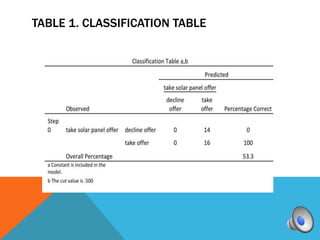
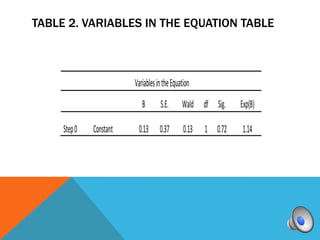
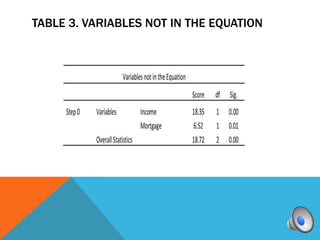
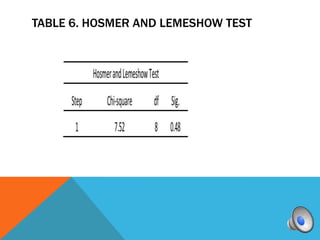
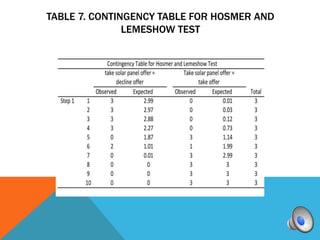
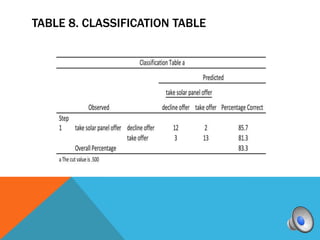
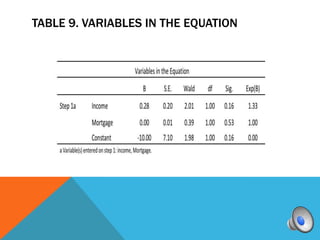
A logistic regression was conducted to predict if homeowners would accept or decline a solar panel offer based on household income and monthly mortgage. The full model was a good fit compared to the constant model. While the predictors were not individually significant, they correctly classified 83.3% of cases overall. Higher income was associated with higher odds of accepting the offer.

2. WHAT IS LOGISTIC REGRESSION?
 Logit for short, a specialized form of regression
 used when the dependent variable is dichotomous (has
only two values 0 and 1) and categorical while the
independent variable(s) could be any type
 There are many variables in the business world that are
dichotomous, for example: male or female, to buy or not
to buy, good credit risk or poor credit risks, to take offer
or decline offer, student will succeed or fail, etc.

3. ASSUMPTIONS OF LOGISTIC REGRESSION
 Does not assume a linear relationship between DV and IV
 Dependent variable must be a dichotomy (2 categories)
 Independent variables need not be interval, nor normally
distributed, nor linearly related, nor of equal variance within
each group
 The categories of the DV must be mutually exclusive and
exhaustive such that a case can only be in one group and
every case must be a member of one of the groups

4. GOAL OF LOGISTIC REGRESSION
 logistic regression determines the impact of
multiple independent variables presented
simultaneously to predict membership of one or
other of the two dependent variable categories

6. DESCRIPTION OF THE DATA
 The data used to conduct logistic regression is from a
survey of 30 homeowners conducted by an electricity
company about an offer of roof solar panels with a 50%
subsidy from the state government as part of the state’s
environmental policy.
 The variables are:
IVs: household income measured in units of a thousand
dollars age of householder
monthly mortgage
size of family household
DV: whether the householder would take or decline the
offer. Take the offer was coded as 1 and decline the offer
was coded as 0.

7. WHAT IS THE RESEARCH QUESTION?
 to determine whether household income and monthly
mortgage will predict taking or declining the solar panel
offer
 Independent Variables: household income and monthly
mortgage
 Dependent Variables: Take the offer or decline the offer

8. TWO HYPOTHESES TO BE TESTED
There are two hypotheses to test in relation to the
overall fit of the model:
 H0: The model is a good fitting model
 H1: The model is not a good fitting model (i.e.
the predictors have a significant effect)

9. HOW TO PERFORM LOGISTIC REGRESSION IN
SPSS
1) Click Analyze
2) Select Regression
3) Select Binary Logistic
4) Select the dependent variable, the one which is a
grouping variable (0 and 1) and place it into the
Dependent Box, in this case, take or decline offer
5) Enter the predictors (IVs) that you want to test into the
Covariates Box. In this case, Household Income and
Monthly Mortgage
6) Leave Enter as the default method

10. CONTINUATION OF SPSS STEPS
7) If there is any categorical IV, click on Categorical button
and enter it. There is none in this case.
8) In the Options button, select Classification Plots, Hosmer-
Lemeshow goodness-of-fit, Casewise Listing of residuals.
Retain default entries for probability of stepwise,
classification cutoff, and maximum iterations
9) Continue, then, OK

12. TABLE 1. CLASSIFICATION TABLE

13. TABLE 2. VARIABLES IN THE EQUATION TABLE

14. TABLE 3. VARIABLES NOT IN THE EQUATION

15. TABLE 4. OMNIBUS TEST OF COEFFICIENTS

16. TABLE 5. MODEL SUMMARY

17. TABLE 6. HOSMER AND LEMESHOW TEST

18. TABLE 7. CONTINGENCY TABLE FOR HOSMER AND
LEMESHOW TEST

19. TABLE 8. CLASSIFICATION TABLE

20. TABLE 9. VARIABLES IN THE EQUATION

22.  A logistic regression analysis was conducted to
predict if householders will take up or decline
the offer of a solar panel subsidy.
 Predictors --household income and mortgage
payment
 A test of the full model against the constant
model was statistically significant, indicating
that the predictors as a set differentiated
between acceptors and decliners of the offer
(chi-square=29, p<.000 with df=2).

23.  Nagelkerke’s R2 of .83 indicated a moderately
strong relationship between prediction and
grouping. Prediction success overall was 83.3%
(85.7% for decline and 81.3% for accept).
 The Wald criterion showed that both predictors
were not significant predictors. ExpB value
indicates that when household income is raised
by one unit ($1,000), the odds ratio is 1.33 times
as large and therefore householders are 1.33
more times likely to take the offer.

24.  Since the predictors did not have a significant effect
(p>.005), we fail to reject the null hypothesis that
there is no difference between observed and model-
predicted values, thus, the model is a good fitting
model. Even if the two predictors did not show
significant effect, they were able to distinguished
between acceptors and decliners of the offer as the
Chi-square table (Table 4) show.
 Perhaps, other predictors such as age and family
size may have significant effect, or perhaps adding
one more predictor, however, this paper only
considered two independent variables.