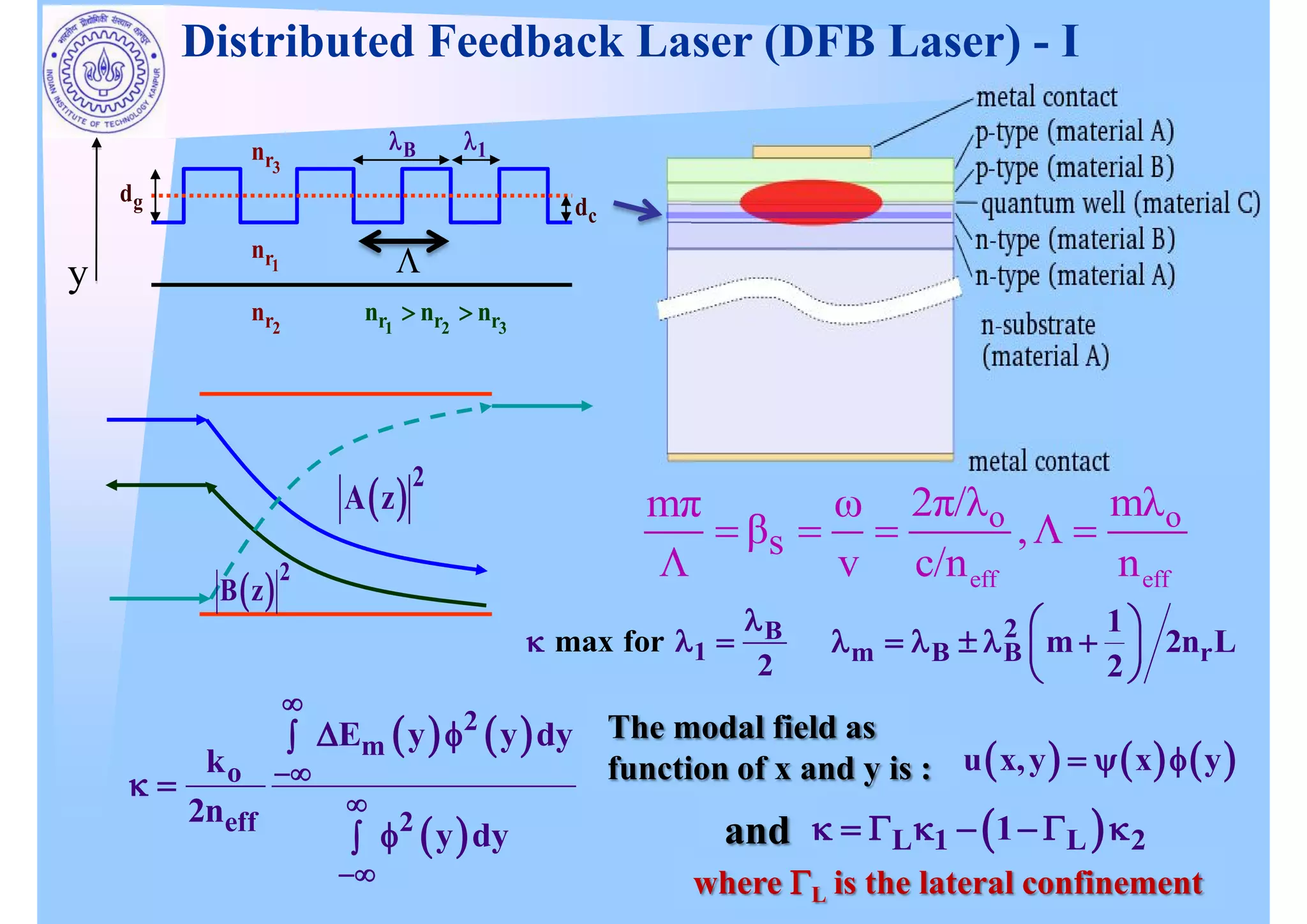
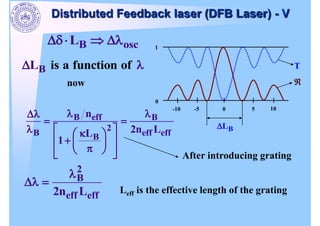
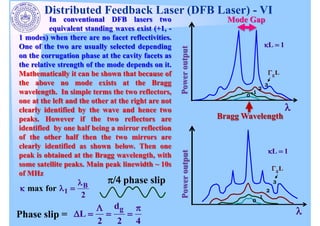
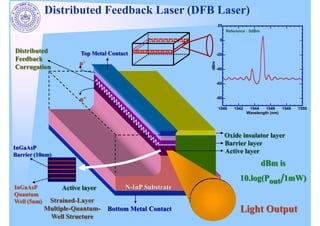
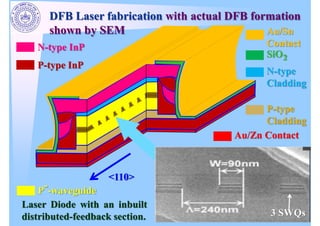
The document discusses distributed feedback lasers (DFB lasers). It provides the modal field equation, effective refractive index equation, and solution for the wave propagation. It describes the grating period, coupling coefficient, and phase mismatching factor. It discusses Bragg wavelength, reflectance, and how reflectance depends on the coupling coefficient and laser length. It also discusses phase slip, conventional DFB lasers with two modes, and fabrication of DFB lasers with a scanning electron microscope image.

1. 2
m
o
2
eff
E y y dy
k
2n
y dy
u x,y x y
2
A z
2
B z
2
m B B r
1
m 2n L
2
L 1 L 2
1
and
where L is the lateral confinement
B
1
max for
2
Distributed Feedback Laser (DFB Laser) - I
The modal field as
function of x and y is :
eff eff
o o
s
2
m
v c/n n
3
r
n
1
r
n
2
r
n
1 2 3
r r r
n n n
B 1
g
d
c
d
y

2. The effective refractive index is o
2 z
n z n ncos
2 2 2
o r o r
k n jk n o
o
2
k o r
k n where is the loss
The solution of the wave which have the forward and backward
propagation is
Distributed Feedback laser (DFB Laser) - II
o o
j z j z
E z R z e S z e
Backward Forward
o o
2q
where is the grating period, and the Cos function is the first Fourier
component of the rectangular perturbation
q is the number of period required to form
with fundamental mode as q = 1
2 2 2 z
j 4 cos where is the coupling coefficient
and is the measure of the power
coupled between the forward and
backward wave
and and
o
o o
k n
, k n
2
where

3. 2 2
o
o
o
2
The phase mismatching factor is given as
eq
o
2n q
any is given by
Where q is the mode of back scattering and is the period of grating
eq
o B
1 1
2 n
Where B is the Bragg Wavelength,
where
B
1 q If q = 1 then
B =
If is the absorption coefficient (Loss)
z z
1 2
R z r e r e
z z
1 2
S z s e s e
and
2
2 2
j
2
S 0
r
R 0
The reflection coefficient is given as
Distributed Feedback laser (DFB Laser) - III

4. The reflection coefficient is given as
S 0
r
R 0
j 2 L j 2 L j
o B o B
o B o B
j 2 L j
o B
B o o B
r e cosh L j r e j e sinh z L
2
r
cosh L j r e sinh L e
2
j
r r e
r can be expressed as
2
2
2 B
2
2
2 2 *
B B
tanh L
R r
tanh L 2Re r tanh L
2 2
The reflectance is given as
At = o = (q / i.e., the Bragg condition is satisfied, then
2
o B
R tanh L
Distributed Feedback laser (DFB Laser) - IV

5. B osc
L
5
-5 10
-10 0
0
1
B
L
T
B is a functio f
L n o
now
B eff B
2
B eff eff
B
n
2n L
L
1
After introducing grating
2
B
eff eff
2n L Leff is the effective length of the grating
Distributed Feedback laser (DFB Laser) - V

6. phase slip
Phase slip =
g
d
L
2 2 4
B
1
max for
2
Distributed Feedback Laser (DFB Laser) - VI
In conventional DFB lasers two
equivalent standing waves exist (+1, -
1 modes) when there are no facet reflectivities.
One of the two are usually selected depending
on the corrugation phase at the cavity facets as
the relative strength of the mode depends on it.
Mathematically it can be shown that because of
the above no mode exists at the Bragg
wavelength. In simple terms the two reflectors,
one at the left and the other at the right are not
clearly identified by the wave and hence two
peaks. However if the two reflectors are
identified by one half being a mirror reflection
of the other half then the two mirrors are
clearly identified as shown below. Then one
peak is obtained at the Bragg wavelength, with
some satellite peaks. Main peak linewidth ~ 10s
of MHz
gL
L 1
Bragg Wavelength
Mode Gap
Power
output
gL
L 1
Power
output

7. Light Output
Bottom Metal Contact
Top Metal Contact
Oxide insulator layer
Barrier layer
Active layer
N-InP Substrate
InGaAsP
Barrier (10nm)
InGaAsP
Quantum
Well (5nm)
Active layer
p+
n+
Distributed
Feedback
Corrugation
Strained-Layer
Multiple-Quantum-
Well Structure
Distributed Feedback Laser (DFB Laser)
-80
-60
-40
-20
0
20
1540 1542 1544 1546 1548 1550
Wavelength (nm)
Reference : 0dBm
dBm is
10.log(Pout/1mW)

8. DFB Laser fabrication with actual DFB formation
shown by SEM
Laser Diode with an inbuilt
distributed-feedback section.
Au/Sn
Contact
N-type InP
P-type InP
SiO2
N-type
Cladding
P-type
Cladding
Au/Zn Contact
<110>
P--waveguide
3 SWQs

9. Chirp in DFB Lasers
S. J. Wang, L. J. P. Ketelsen, V. R. McCrary, Y. Twu, S. G. Napholtz, and W. V. Werner,
IEEE Photon. Technol. Lett., vol. 2(11), 775(1990).