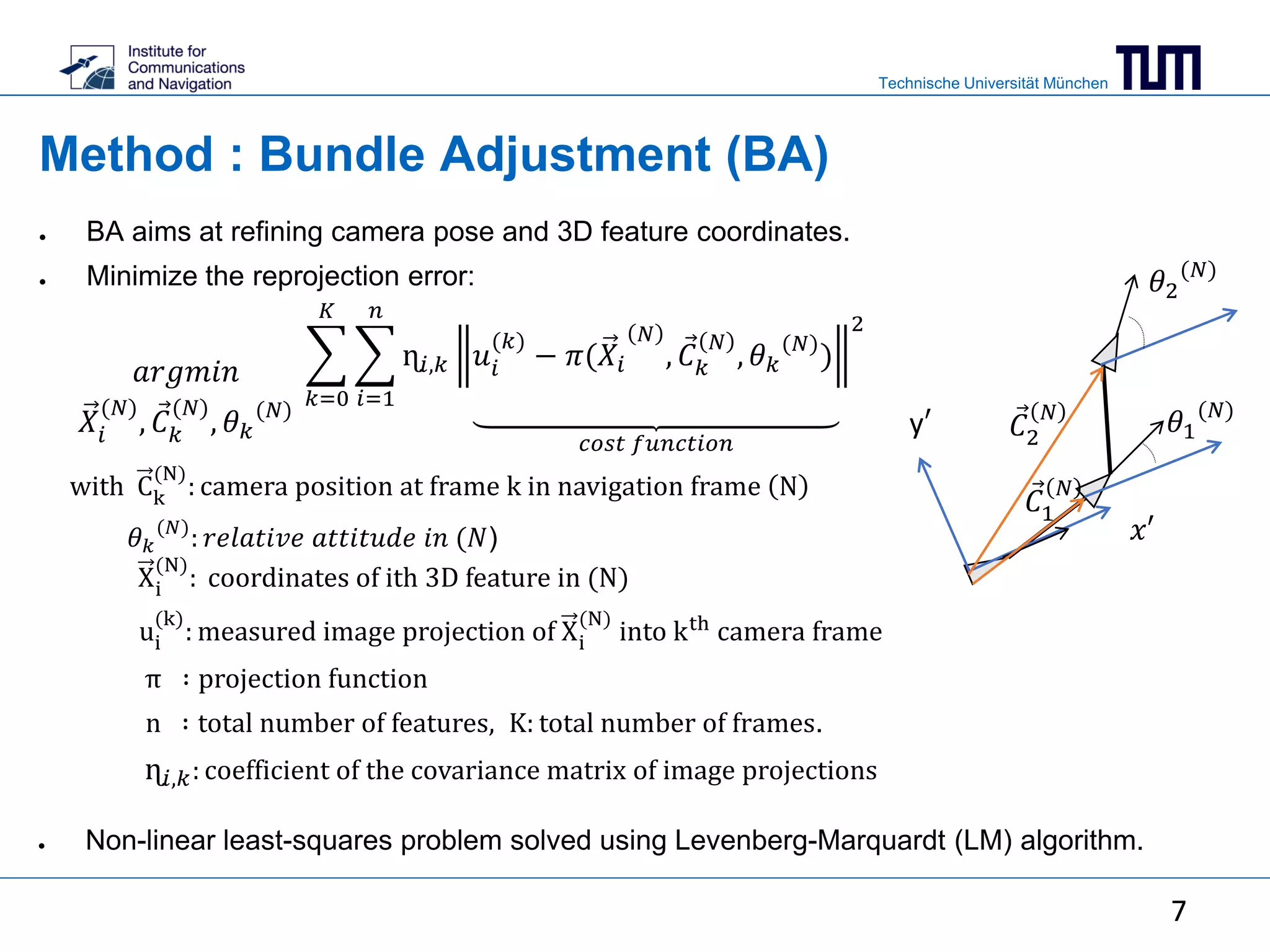
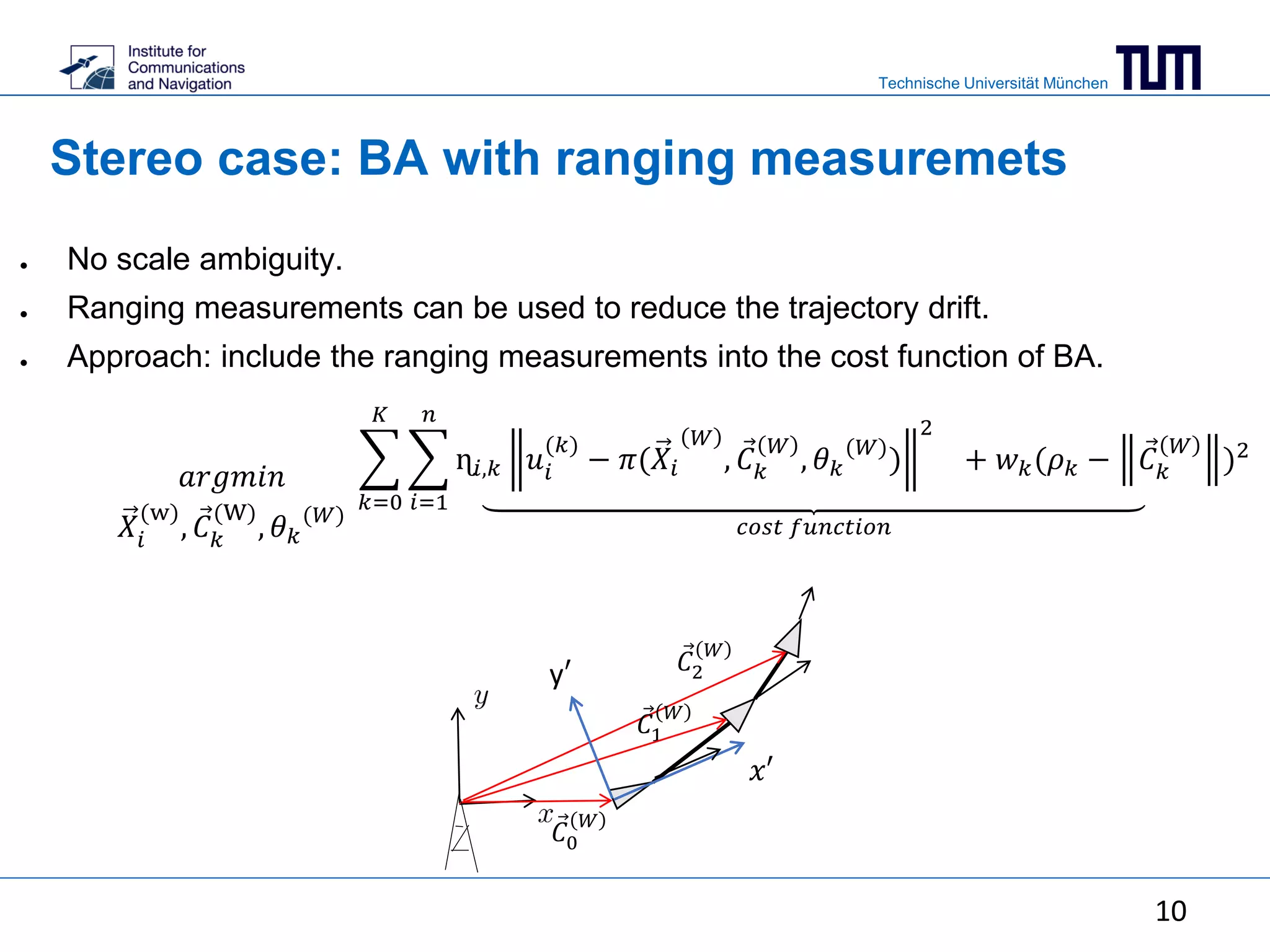
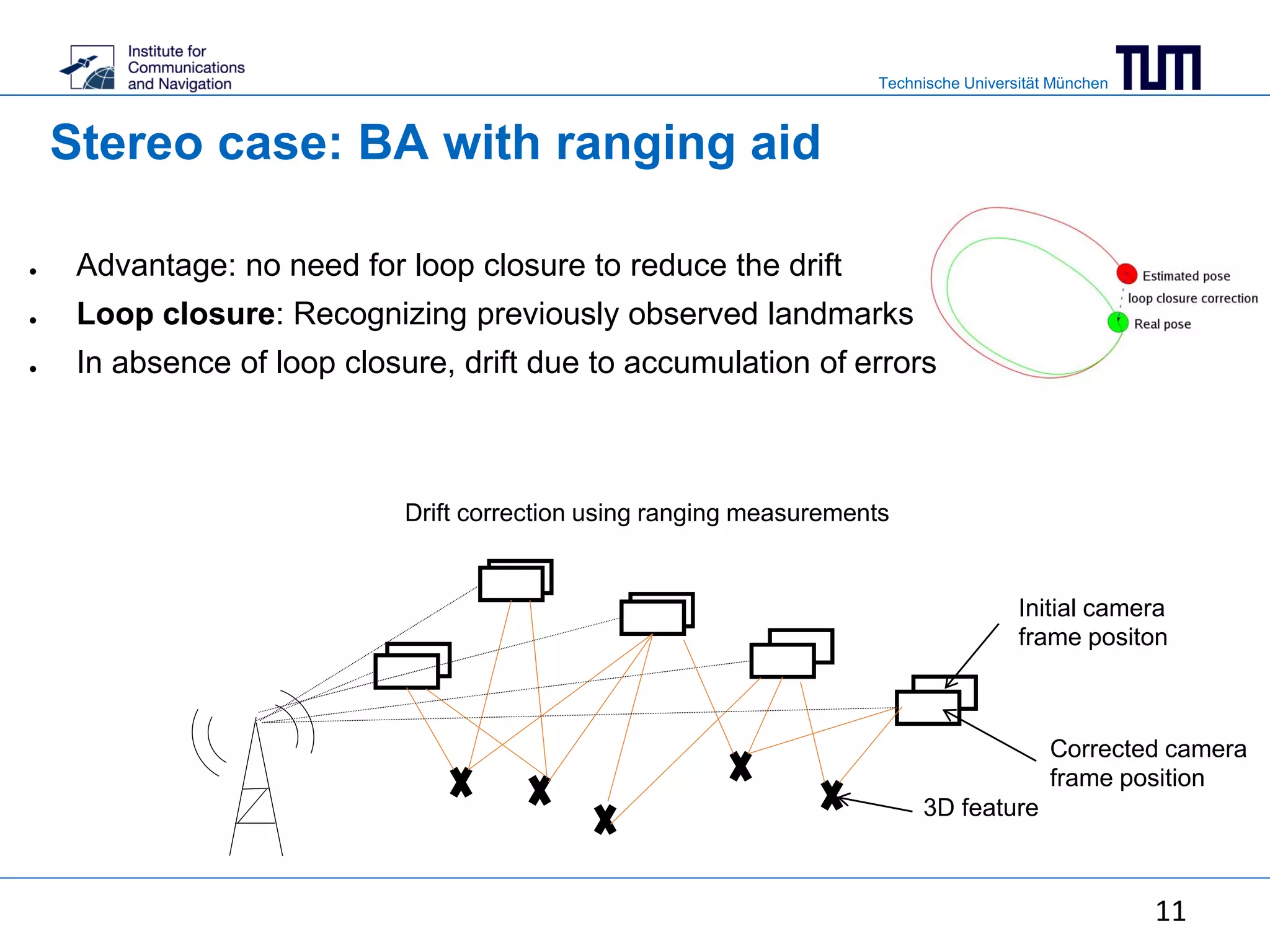
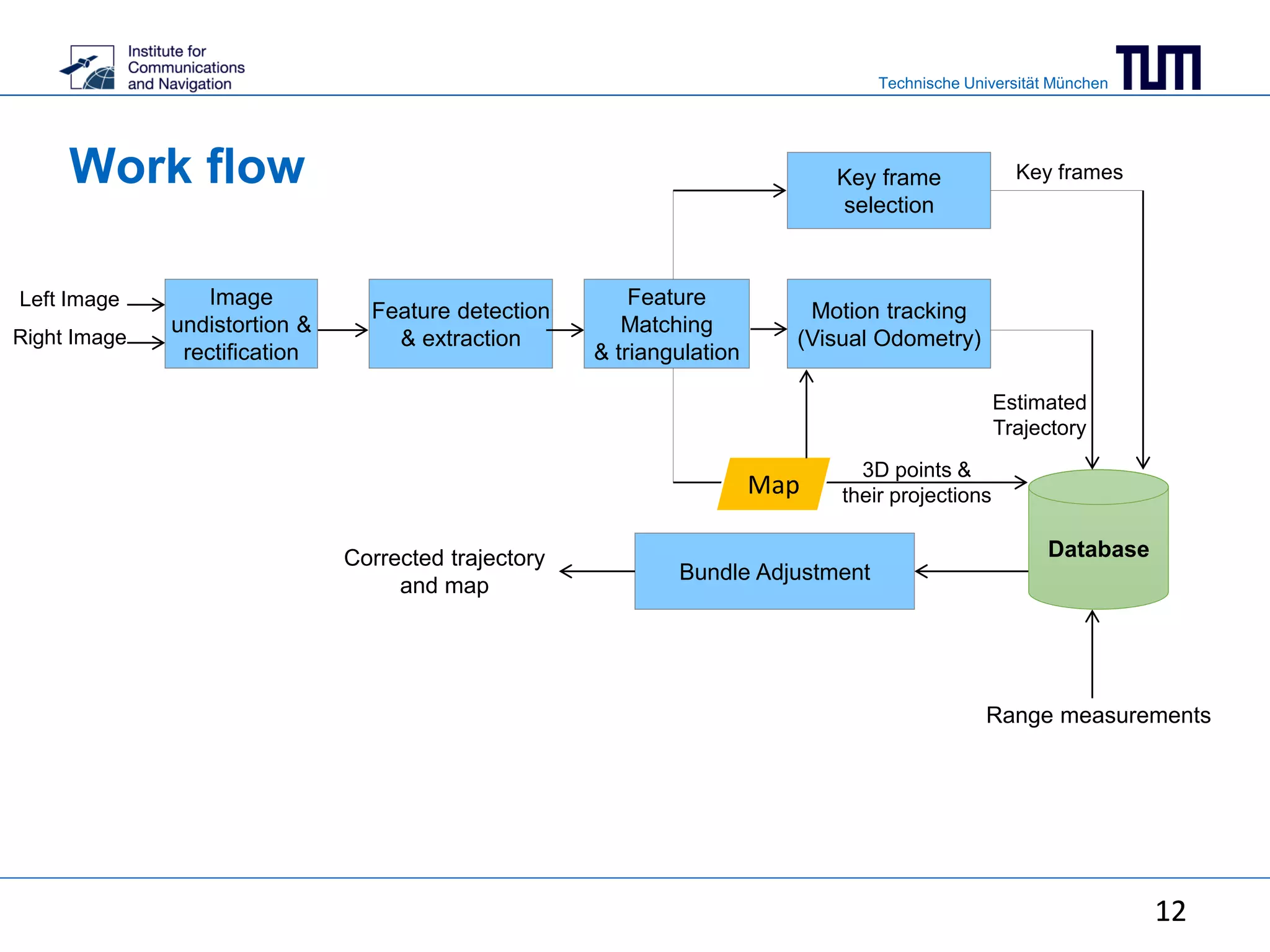
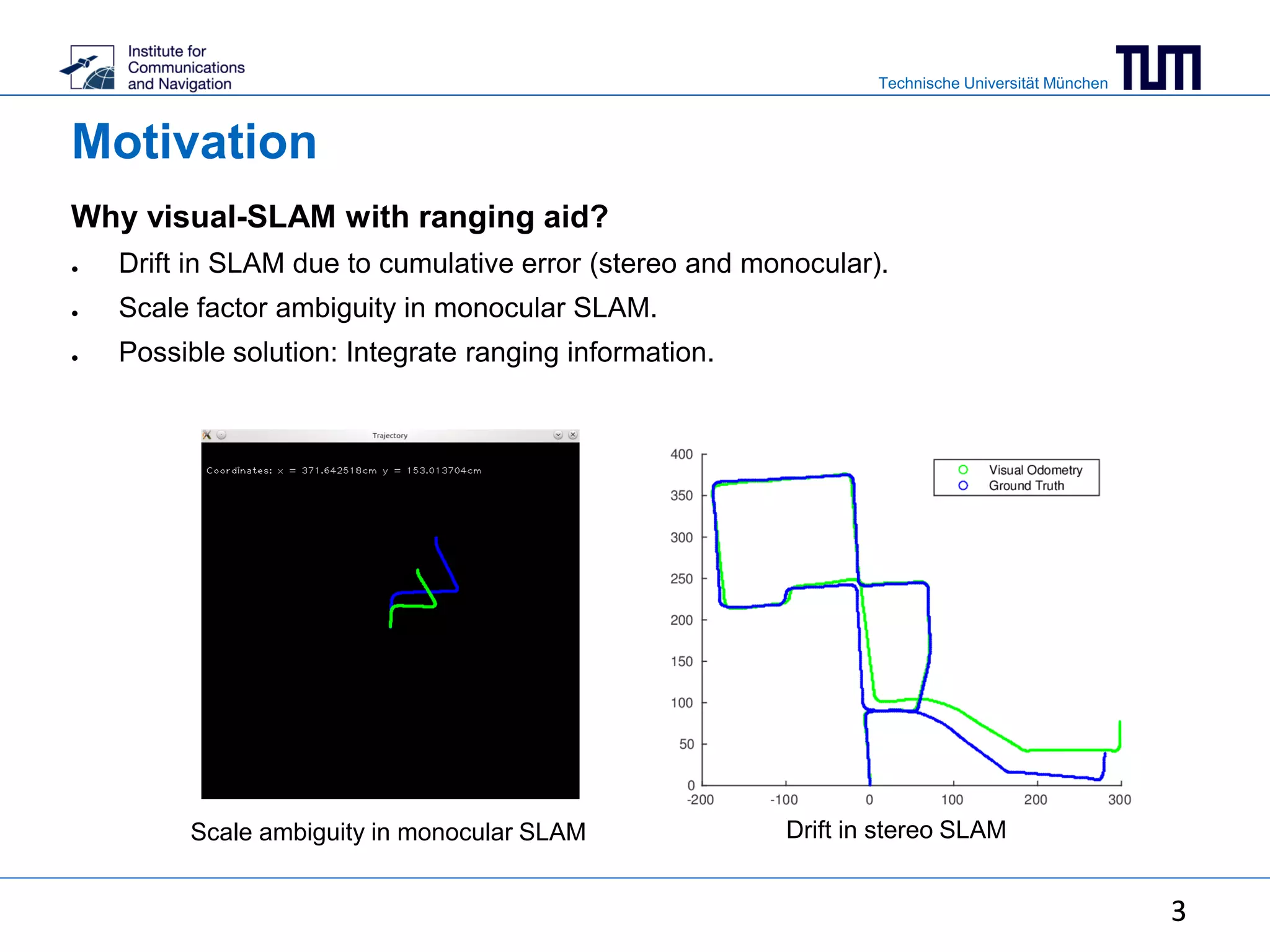
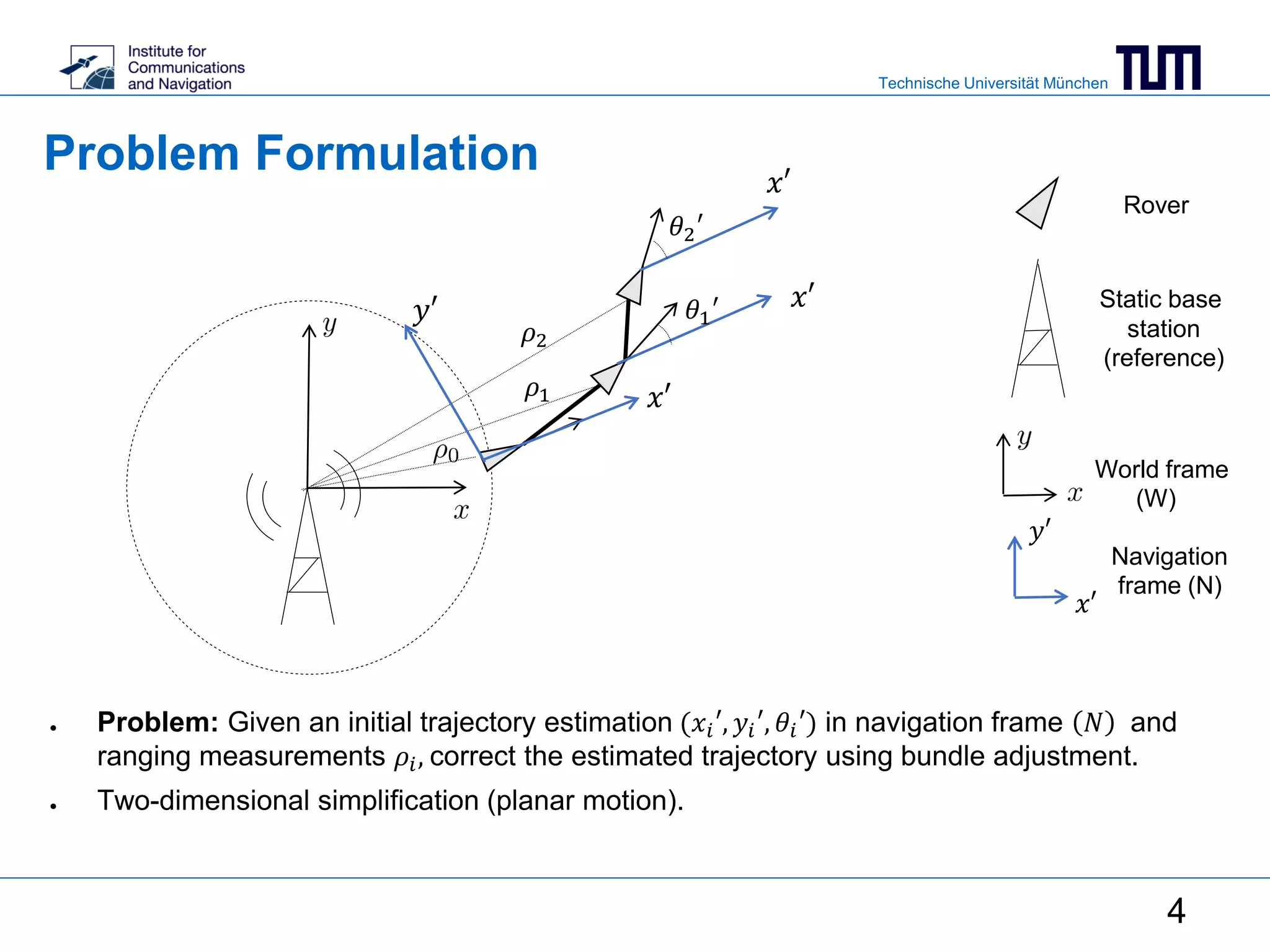
This document summarizes a master's thesis on using ranging measurements to aid monocular and stereo visual simultaneous localization and mapping (SLAM). The thesis aims to reduce drift in estimated trajectories by integrating ranging measurements into bundle adjustment. For monocular SLAM, ranging is used to resolve scale ambiguity, while for stereo SLAM it is directly included in the bundle adjustment cost function. Experimental results demonstrate reduced reprojection error through bundle adjustment of 3168 points over 100 frames using a visual-inertial sensor.

1. Technische Universität München
Master thesis : Mono- and stereo-camera
SLAM with ranging aid
Chiraz Nafouki Supervisors: Dr. Gabriele Giorgi
chiraz.nafouki@tum.de gabriele.giorgi@tum.de
M.Sc. Chen Zhu
chen.zhu@tum.de
Mid-term presentation
26/07/2016

2. Technische Universität München
Outline
1. Motivation
2. Problem Formulation
3. Method: Bundle Adjustment (BA)
4. Related work: Monocular SLAM with ranging aid
5. BA for stereo SLAM with ranging aid
6. Work flow
7. Experimental results

3. Technische Universität München
3
Motivation
Why visual-SLAM with ranging aid?
● Drift in SLAM due to cumulative error (stereo and monocular).
● Scale factor ambiguity in monocular SLAM.
● Possible solution: Integrate ranging information.
Scale ambiguity in monocular SLAM Drift in stereo SLAM
3

4. Technische Universität München
Problem Formulation
Static base
station
(reference)
Rover
● Problem: Given an initial trajectory estimation (𝑥𝑖′, 𝑦𝑖′, 𝜃𝑖′) in navigation frame 𝑁 and
ranging measurements 𝜌𝑖, correct the estimated trajectory using bundle adjustment.
● Two-dimensional simplification (planar motion).
𝜌1
𝜌2
𝜃1′
𝑥′
𝑦′
𝑥′
𝑦′
World frame
(W)
Navigation
frame (N)
𝜃2′
𝑥′
𝑥′
4

5. Technische Universität München
Problem Formulation
Static base
station
(reference)
Rover
● Absolute attitude (𝛼0) ambiguity: Trajectory can be rotated around the base station with
ranging measurements invariance.
● Assumption: Rover starts at 𝑟0 1,0 .
𝛼0
𝛼0
𝛼0
𝑥′
𝑥′
𝑥′
𝑦′
𝑦′
𝑦′
5
𝑟0

6. Technische Universität München
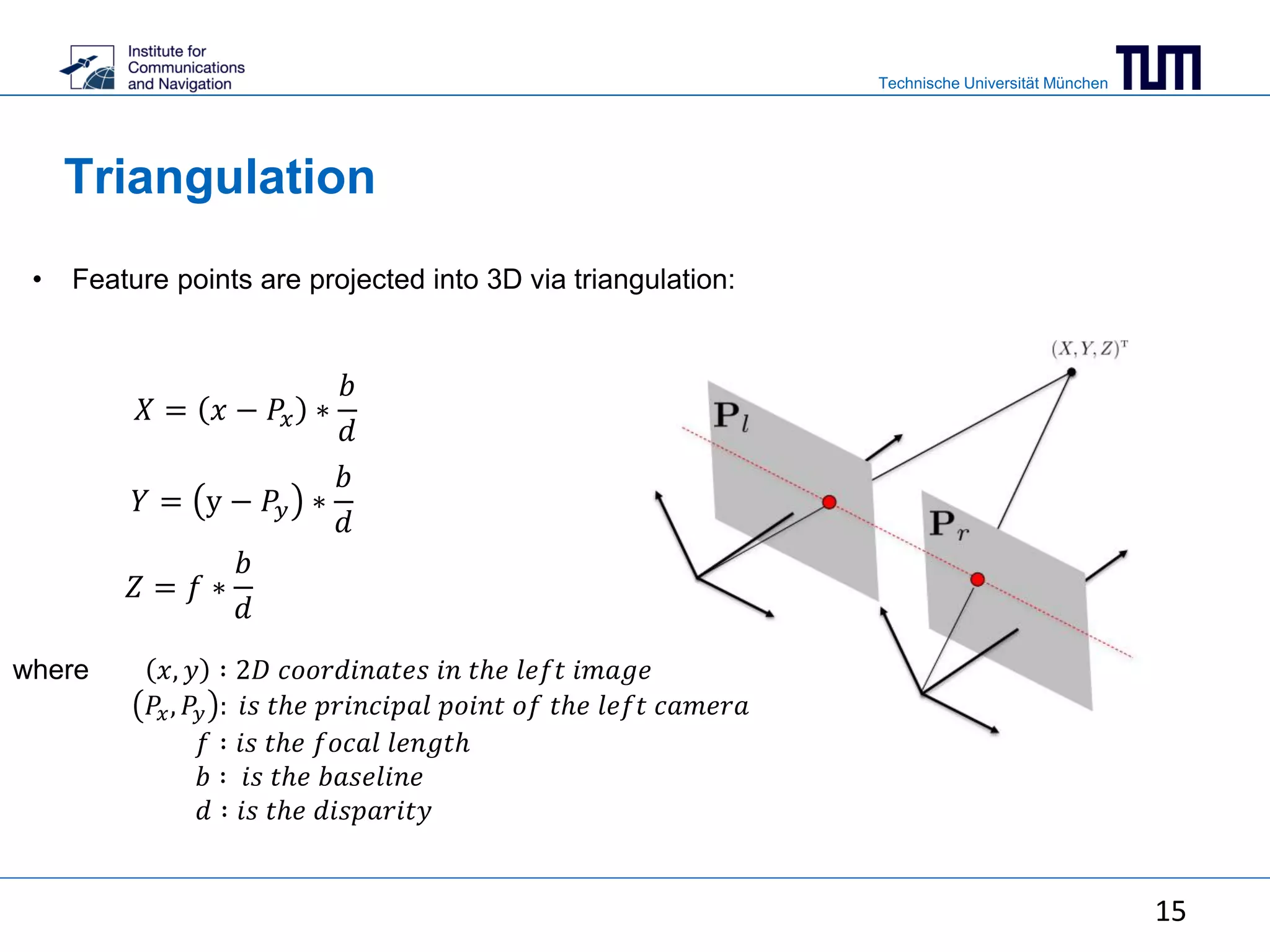
Projection of world coordinates into image
coordinates
𝑢 =
𝑥
𝑦
1
= 𝜋 𝑿, R, 𝐭 = P𝐗 = K[R 𝒕]𝐗 =
−𝑓 0 𝑃𝑥
0 −𝑓 𝑃𝑦
0 0 1
[R 𝒕]
𝑋
𝑌
𝑍
1
𝑢: ℎ𝑜𝑚𝑜𝑔𝑒𝑛𝑒𝑜𝑢𝑠 𝑖𝑚𝑎𝑔𝑒 𝑐𝑜𝑜𝑟𝑑𝑖𝑛𝑎𝑡𝑒𝑠
𝑿: 3𝐷 𝑝𝑜𝑖𝑛𝑡 𝑐𝑜𝑜𝑟𝑑𝑖𝑛𝑎𝑡𝑒𝑠
𝑅, 𝒕 ∶ 𝑟𝑜𝑡𝑎𝑡𝑖𝑜𝑛 𝑎𝑛𝑑 𝑡𝑟𝑎𝑛𝑠𝑙𝑎𝑡𝑖𝑜𝑛
𝜋: 𝑝𝑟𝑜𝑗𝑒𝑐𝑡𝑖𝑜𝑛 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛
𝑃: 𝑝𝑟𝑜𝑗𝑒𝑐𝑡𝑖𝑜𝑛 𝑚𝑎𝑡𝑟𝑖𝑥
𝐾: 𝑐𝑎𝑚𝑒𝑟𝑎 𝑚𝑎𝑡𝑟𝑖𝑥
𝑓: 𝑓𝑜𝑐𝑎𝑙 𝑙𝑒𝑛𝑔𝑡ℎ
(𝑃𝑥 , 𝑃𝑦): 𝑝𝑟𝑖𝑛𝑐𝑖𝑝𝑎𝑙 𝑝𝑜𝑖𝑛𝑡 𝑐𝑜𝑜𝑟𝑑𝑖𝑛𝑎𝑡𝑒𝑠
6

7. Technische Universität München
7
Method : Bundle Adjustment (BA)
with Ck
(N)
: camera position at frame k in navigation frame N
𝜃 𝑘
(𝑁)
: 𝑟𝑒𝑙𝑎𝑡𝑖𝑣𝑒 𝑎𝑡𝑡𝑖𝑡𝑢𝑑𝑒 𝑖𝑛 (𝑁)
Xi
(N)
: coordinates of ith 3D feature in (N)
ui
(k)
: measured image projection of Xi
(N)
into kth
camera frame
π ∶ projection function
n ∶ total number of features, K: total number of frames.
ɳ𝑖,𝑘: coefficient of the covariance matrix of image projections
𝑎𝑟𝑔𝑚𝑖𝑛
𝑋𝑖
(𝑁)
, 𝐶 𝑘
(𝑁)
, 𝜃 𝑘
(𝑁)
𝑐𝑜𝑠𝑡 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛
𝑘=0
𝐾
𝑖=1
𝑛
ɳ𝑖,𝑘 𝑢𝑖
(𝑘)
− 𝜋(𝑋𝑖
𝑁
, 𝐶 𝑘
𝑁
, 𝜃 𝑘
(𝑁)
)
2
𝑥′
● BA aims at refining camera pose and 3D feature coordinates.
● Minimize the reprojection error:
● Non-linear least-squares problem solved using Levenberg-Marquardt (LM) algorithm.
𝐶1
𝑁
𝐶2
𝑁
y′
7
𝜃1
(𝑁)
𝜃2
(𝑁)

8. Technische Universität München
8
Related Work : Scale estimation in monocular
SLAM with ranging measurements
𝑟𝑘 = 𝐶 𝑘
𝑊
= 𝑓 𝐶 𝑘
𝑁
, 𝑠, 𝛼0, 𝑟0 = 𝑓𝑘 𝛏 , 𝑤𝑖𝑡ℎ 𝛏 = 𝑠, 𝛼0, 𝑟0
● Solving this LS problem gives us 𝐶 𝑘
(𝑁)
only up to a scale 𝑠.
● Approach: Use ranging measurements to find 𝑠.
● The distance 𝑟𝑘 between the rover and the base station at frame 𝑘 :
● Solve the non-linear minimization problem using LM algorithm:
𝑎𝑟𝑔𝑚𝑖𝑛
𝜉
k=0
𝐾
𝑤 𝑘(𝜌 𝑘 − 𝑓𝑘 𝝃 )2
Find minimizer 𝝃 and therefore scale 𝑠.
𝑖=1
𝑛
ɳ𝑖,𝑘 𝑢𝑖
(𝑘)
− 𝜋(𝑋𝑖
𝑁
, 𝐶 𝑘
𝑁
, 𝜃 𝑘
(𝑁)
)
2
𝑎𝑟𝑔𝑚𝑖𝑛
𝐶 𝑘
(𝑁)
, 𝜃 𝑘
(𝑁)
𝑟1
𝑟2
𝛼0
𝑟0 𝑥′
y′
8

9. Technische Universität München
9
𝑎𝑟𝑔𝑚𝑖𝑛
𝜉
k=0
𝐾
𝑤 𝑘(𝜌 𝑘 − 𝑓𝑘 𝝃 )2
Disadvantages of this approach :
● Local optimization of the reprojection error
● Ranging measurements are exploited for scale correction
𝑎𝑟𝑔𝑚𝑖𝑛
𝐶 𝑘
(𝑁)
, 𝜃 𝑘
(𝑁) 𝑖=1
𝑛
ɳ𝑖,𝑘 𝑢𝑖
(𝑘)
− 𝜋(𝑋𝑖
𝑁
, 𝐶 𝑘
𝑁
, 𝜃 𝑘
(𝑁)
)
2
9
Related Work : Scale estimation in monocular
SLAM with ranging measurements
with 𝑓𝑘 𝝃 = 𝐶 𝑘
𝑊
, 𝛏 = 𝑠, 𝛼0, 𝑟0

10. Technische Universität München
Stereo case: BA with ranging measuremets
● No scale ambiguity.
● Ranging measurements can be used to reduce the trajectory drift.
● Approach: include the ranging measurements into the cost function of BA.
𝑘=0
𝐾
𝑖=1
𝑛
ɳ𝑖,𝑘 𝑢𝑖
(𝑘)
− 𝜋(𝑋𝑖
𝑊
, 𝐶 𝑘
𝑊
, 𝜃 𝑘
(𝑊)
)
2
+ 𝑤 𝑘(𝜌 𝑘 − 𝐶 𝑘
𝑊
)2
𝑐𝑜𝑠𝑡 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛
𝑎𝑟𝑔𝑚𝑖𝑛
𝑋𝑖
(w)
, 𝐶 𝑘
(W)
, 𝜃 𝑘
(𝑊)
10
𝐶1
𝑊
𝐶2
𝑊
𝑥′
y′
𝐶0
𝑊

11. Technische Universität München
Initial camera
frame positon
3D feature
Corrected camera
frame position
Drift correction using ranging measurements
● Advantage: no need for loop closure to reduce the drift
● Loop closure: Recognizing previously observed landmarks
● In absence of loop closure, drift due to accumulation of errors
Stereo case: BA with ranging aid
11

12. Technische Universität München
12
Work flow
Feature detection
& extraction
Motion tracking
(Visual Odometry)
Bundle Adjustment
Feature
Matching
& triangulation
Key frame
selection
Database
Left Image
Range measurements
Right Image
Image
undistortion &
rectification
Key frames
Estimated
Trajectory
3D points &
their projectionsMap
Corrected trajectory
and map
12

13. Technische Universität München
Image undistortion and rectification
• Compute the affine transformation that reduces radial and tangential distortions.
• Compute the rotations such that corresponding epipolar lines are aligned
horizontally (epipolar constraint).
13

14. Technische Universität München
14
Feature detection & extraction
Feature Matching
● Feature detector uses a corner detector (Harris detector)
● Feature descriptor uses response to a Sobel filter.
● Matching is based on the sum of absolute differences (SAD).
● Matching is done between the left and right images and between two consecutive frames.
Feature matching between left and right camera images using LIBVISO2 library
14

15. Technische Universität München
Triangulation
• Feature points are projected into 3D via triangulation:
15
𝑋 = 𝑥 − 𝑃𝑥 ∗
𝑏
𝑑
𝑌 = y − 𝑃𝑦 ∗
𝑏
𝑑
𝑍 = 𝑓 ∗
𝑏
𝑑
where 𝑥, 𝑦 ∶ 2𝐷 𝑐𝑜𝑜𝑟𝑑𝑖𝑛𝑎𝑡𝑒𝑠 𝑖𝑛 𝑡ℎ𝑒 𝑙𝑒𝑓𝑡 𝑖𝑚𝑎𝑔𝑒
𝑃𝑥, 𝑃𝑦 : 𝑖𝑠 𝑡ℎ𝑒 𝑝𝑟𝑖𝑛𝑐𝑖𝑝𝑎𝑙 𝑝𝑜𝑖𝑛𝑡 𝑜𝑓 𝑡ℎ𝑒 𝑙𝑒𝑓𝑡 𝑐𝑎𝑚𝑒𝑟𝑎
𝑓 ∶ 𝑖𝑠 𝑡ℎ𝑒 𝑓𝑜𝑐𝑎𝑙 𝑙𝑒𝑛𝑔𝑡ℎ
𝑏 ∶ 𝑖𝑠 𝑡ℎ𝑒 𝑏𝑎𝑠𝑒𝑙𝑖𝑛𝑒
𝑑 ∶ 𝑖𝑠 𝑡ℎ𝑒 𝑑𝑖𝑠𝑝𝑎𝑟𝑖𝑡𝑦

16. Technische Universität München
Motion tracking (Visual Odometry)
• Use of LIBVISO2: C++ Library for Visual Odometry.
• Camera motion (R, t) is estimated by minimizing the sum of reprojection error:
• Solve through Gauss-Newton optimization method.
• RANSAC is applied for more robustness.
𝑖=1
𝑛
𝑢𝑖
(l)
− 𝜋(𝑙)(𝑋𝑖 ; 𝑅, 𝐭)
2
+ 𝑢𝑖
(r)
− 𝜋(𝑟)(𝑋𝑖 ; 𝑅, 𝐭)
2
16

17. Technische Universität München
17
Ranging measurements
For real experiments, use a checkboard as fixed reference and measure the distance to it:
● Detect checkboard (using OpenCV)
● Calculate distance 𝑑 to checkboard (m):
17
with 𝑓: 𝑓𝑜𝑐𝑎𝑙 𝑙𝑒𝑛𝑔𝑡ℎ 𝑚
𝐿: 𝑔𝑟𝑖𝑑 𝑠𝑖𝑧𝑒 𝑖𝑛 𝑚𝑒𝑡𝑟𝑖𝑐 𝑚
𝑙: 𝑔𝑟𝑖𝑑 𝑠𝑖𝑧𝑒 𝑖𝑛 𝑖𝑚𝑎𝑔𝑒 𝑝𝑖𝑥𝑒𝑙𝑠
𝒅 =
𝒇 ∗ 𝑳
𝒍

18. Technische Universität München
18
Ranging measurements
0
1
2
3
4
5
6
7
8
9
0 50 100 150 200
Error(cm)
True distance to the checkboard (cm)
• Ranging measurement error increases with distance to
checkboard.
• Problem of checkboard detection.

19. Technische Universität München
19
Experimental Set up
● VI-Sensor: Visual-Inertial Sensor
● Calibrated stereo camera
● Resolution: 752 × 480
● Frame rate: 20 fps
● Interface the Sensor From ROS
19

20. Technische Universität München
Experimental Results
Results using VI-Sensor
• BA for 3168 3D points and 100 frames
• Computation time 43 seconds
• 50 iterations for LM algorithm
• Reduction of the reprojection error from 6007,84 to 192,894
• Implementation of work flow (without ranging measurement and without keyframes
selection)
• Implementation of Bundle adjustment using the Sparse Bundle Adjustment (sba)
C++ package
• Estimation of the initial and final total reprojection error

21. Technische Universität München
21
Experimental Results
Results on Karlsruhe dataset (KITTI dataset)
• Stereo sequence recorded from a moving vehicle
• Calibration parameters and ground Truth provided
• BA for 52672 3D points and 250 frames
• Computation time 111,43 seconds
• 150 iterations for LM algorithm
• Reduction of the reprojection error from 8093,9 to 21,24
21

22. Technische Universität München
22
Next?
● Integration of ranging measurements and keyframes selection in BA
● Mapping
● Compare with ground truth and other approaches
Optional:
● Try other feature detectors/descriptors
● Loop closure detection
● Report and final presentation: end of October
22

23. Technische Universität München
23
References
23
The Design and Implementation of a Generic Sparse Bundle Adjustment Software
Package Based on the Levenberg-Marquardt Algorithm
M.I. A. Lourakis and A.A. Argyros
StereoScan: Dense 3d Reconstruction in Real-time
Andreas Geiger, Julius Ziegler and Christoph Stiller
Visual Odometry Part I: The First 30 Years and Fundamentals
Davide Scaramuzza and Friedrich Fraundorfer
Real-time Monocular SLAM: Why Filter?
Hauke Strasdat, J. M. M. Montiel and Andrew J. Davison