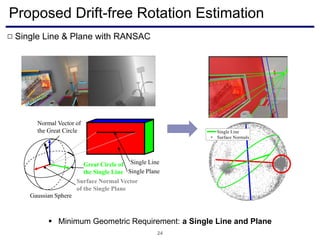
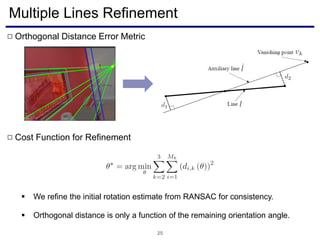
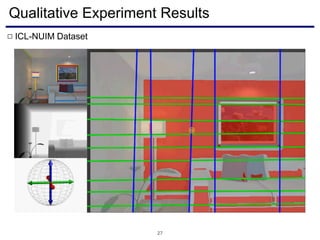
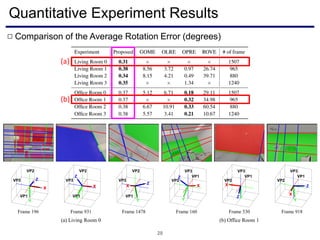
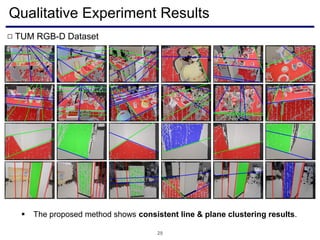
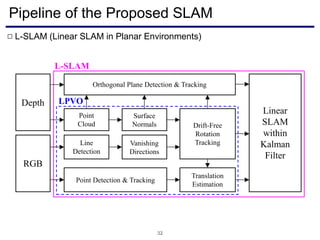
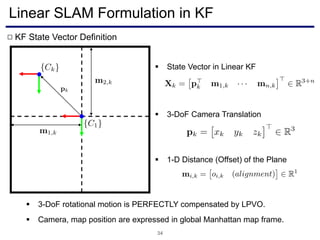
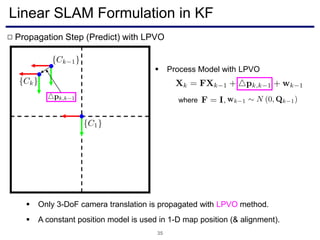
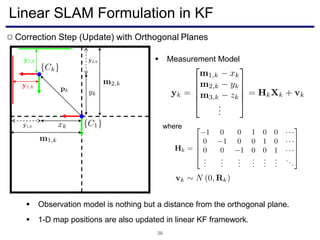
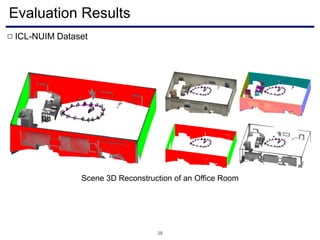
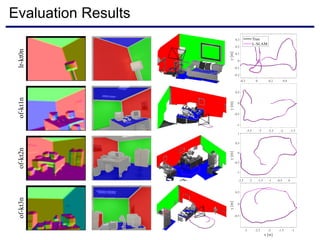
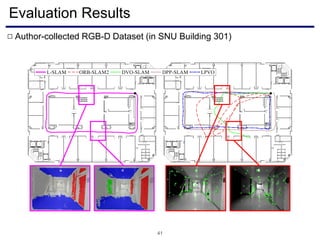
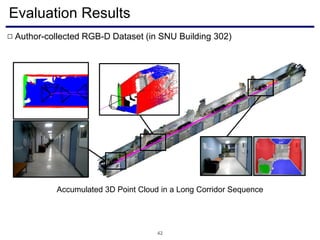
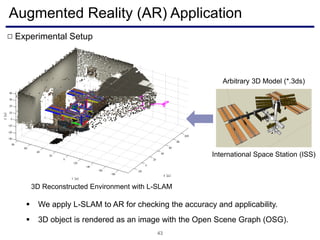
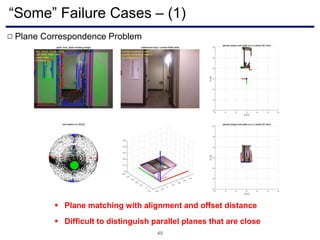
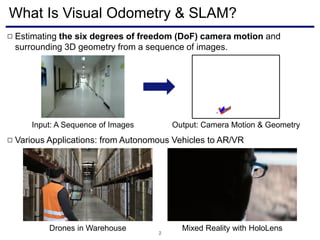
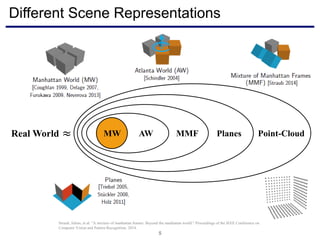
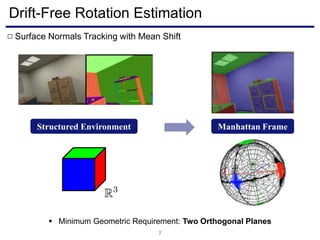
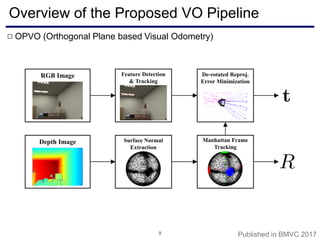
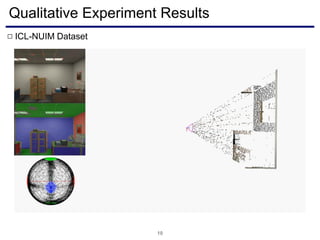
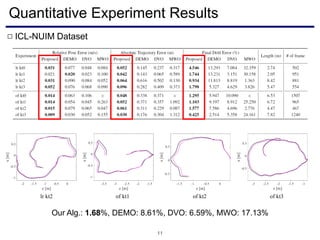
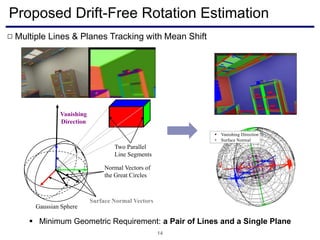
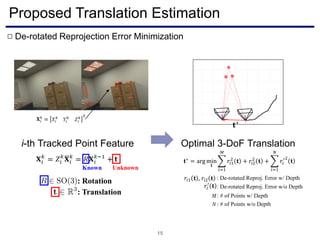
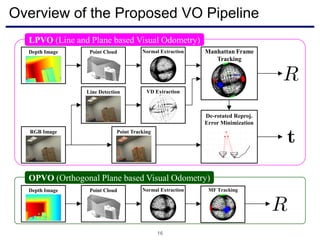
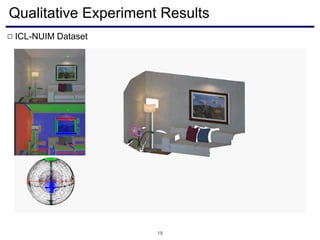
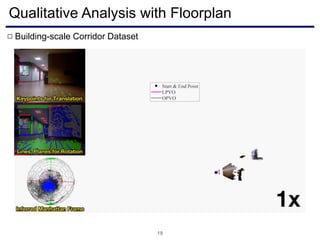
The document discusses a novel approach to visual odometry (VO) and simultaneous localization and mapping (SLAM) that leverages structural information in indoor environments, focusing on drift-free rotation estimation using lines and planes. It presents various algorithms and evaluations, demonstrating the effectiveness of the proposed methods in improving camera orientation and translation accuracy across different datasets. Key contributions include the development of linear SLAM formulations and their applications in augmented reality, addressing challenges in traditional VO and SLAM techniques.

1. Visual Odometry & SLAM Utilizing
Indoor Structured Environments
Seoul National University
Intelligent Control Systems Laboratory
August 14, 2018
Pyojin Kim

2. What Is Visual Odometry & SLAM?
2
Estimating the six degrees of freedom (DoF) camera motion and
surrounding 3D geometry from a sequence of images.
□
Various Applications: from Autonomous Vehicles to AR/VR□
Drones in Warehouse Mixed Reality with HoloLens
Input: A Sequence of Images Output: Camera Motion & Geometry

3. Motivation
3
Rotation is much more important than translation in the camera motion.□
Estimated (left) and True (right) Camera Orientation
The problem of Accurate and Drift-Free Rotation,
Given: Structural information (lines and planes) in indoor environments
Find: Absolute camera orientation
Zhang, Ji, Michael Kaess, and Sanjiv Singh. "A real-time method for depth enhanced visual odometry." Autonomous Robots
41.1 (2017): 31-43.

4. Main Contributions
1. Integration of Drift-Free Rotation Estimation in VO□
2. Absolute Camera Orientation Jointly from Multiple Lines and Planes□
3. Robust Visual Compass from a Single Line and Plane□
Published in BMVC 2017, ICRA 2018, CVPR 2018, and ECCV 2018
4. Linear SLAM Formulation with Absolute Camera Rotation□

5. Different Scene Representations
5
Straub, Julian, et al. "A mixture of manhattan frames: Beyond the manhattan world." Proceedings of the IEEE Conference on
Computer Vision and Pattern Recognition. 2014.
Real World Point-CloudPlanesMMFAWMW≈

6. Manhattan World (MW) Assumption
6
Coughlan, James M., and Alan L. Yuille. "Manhattan world: Compass direction from a single image by bayesian inference."
Computer Vision, 1999. The Proceedings of the Seventh IEEE International Conference on. Vol. 2. IEEE, 1999.
All planes in the scenes are parallel to one of the three major planes of one
common coordinate system.
□

7. Drift-Free Rotation Estimation
7
Surface Normals Tracking with Mean Shift□
 Minimum Geometric Requirement: Two Orthogonal Planes
Structured Environment Manhattan Frame

8. Proposed Translation Estimation
8
De-rotated Reprojection Error Minimization□
i-th Tracked Point Feature
: Translation
: Rotation
UnknownKnown
𝐭∗
Optimal 3-DoF Translation
: De-rotated Reproj. Error w/ Depth
: # of Points w/ Depth
𝑟𝑖1 𝐭 , 𝑟𝑖2 𝐭
𝐭∗
= arg min
𝐭
෍
𝑖=1
𝑀
𝑟𝑖1
2
𝐭 + 𝑟𝑖2
2
𝐭

9. Overview of the Proposed VO Pipeline
9
OPVO (Orthogonal Plane based Visual Odometry)□
RGB Image
Depth Image Surface Normal
Extraction
Feature Detection
& Tracking
Manhattan Frame
Tracking
De-rotated Reproj.
Error Minimization
Published in BMVC 2017

10. Qualitative Experiment Results
10
ICL-NUIM Dataset□

11. Quantitative Experiment Results
11
ICL-NUIM Dataset□
lr kt2 of kt1 of kt2 of kt3
Our Alg.: 1.68%, DEMO: 8.61%, DVO: 6.59%, MWO: 17.13%

12. Problems in Previous OPVO
12
When Camera Looks at only a Single Plane
OPVO requires at least two orthogonal planes to be visible at all times.□
All feature points should have depth information for translation.□

13. Our Solution
13
A New Approach for Drift-Free Rotation from Both Lines and Planes□
A New Way for Accurate Translation on the De-Rotated Reprojection Error□
Evaluation on the Public RGB-D and Author-collected Datasets□
Structured Environment Exhibiting Orthogonal Regularities
Projection
Surface
Normal
PlanesLines Structured Environment
Published in ICRA 2018

14. Proposed Drift-Free Rotation Estimation
14
Multiple Lines & Planes Tracking with Mean Shift□
Gaussian Sphere
Two Parallel
Line Segments
Vanishing
Direction
Surface Normal Vectors
Normal Vectors of
the Great Circles
 Minimum Geometric Requirement: a Pair of Lines and a Single Plane

15. Proposed Translation Estimation
15
De-rotated Reprojection Error Minimization□
i-th Tracked Point Feature
: Translation
: Rotation
UnknownKnown
𝐭∗
Optimal 3-DoF Translation
: De-rotated Reproj. Error w/ Depth
: De-rotated Reproj. Error w/o Depth
: # of Points w/ Depth
: # of Points w/o Depth
𝑟𝑖1 𝐭 , 𝑟𝑖2 𝐭
𝑟𝑖
′
𝐭
𝐭∗
= arg min
𝐭
෍
𝑖=1
𝑀
𝑟𝑖1
2
𝐭 + 𝑟𝑖2
2
𝐭 + ෍
𝑖=1
𝑁
𝑟𝑖
′2
𝐭

16. Overview of the Proposed VO Pipeline
16
Point Tracking
Line Detection
Normal ExtractionDepth Image
RGB Image
VD Extraction
Manhattan Frame
Tracking
Point Cloud
De-rotated Reproj.
Error Minimization
LPVO (Line and Plane based Visual Odometry)
Normal ExtractionDepth Image Point Cloud MF Tracking
OPVO (Orthogonal Plane based Visual Odometry)

17. Experiment Setup
ICL-NUIM Dataset (~9.01 m)
TUM RGB-D Dataset (~22.14 m)
Building-scale Corridor Dataset (~120 m)
: only a single plane
 We compare LPVO with ORB(1), DEMO(2), DVO(3), MWO(4), OPVO(5).
(1) R. Mur-Artal et al. ORB-SLAM: a versatile and accurate monocular slam system. IEEE T-RO, (2015)
(2) J. Zhang et al. A real-time method for depth enhanced visual odometry. AURO, (2017)
(3) C. Kerl et al. Robust odometry estimation for rgb-d cameras. ICRA, (2013)
(4) Y. Zhou et al. Efficient density-based tracking of 3D sensors in Manhattan worlds. ACCV, (2016)
(5) P. Kim et al. Visual odometry with drift-free rotation estimation using indoor scene regularities. BMVC, (2017)

18. Qualitative Experiment Results
18
ICL-NUIM Dataset□

19. Qualitative Analysis with Floorplan
19
Building-scale Corridor Dataset□

20. Qualitative Analysis with Floorplan
20
Only LPVO can
estimate 6-DoF
Nearly 8x
more accurate
Building-scale Corridor Dataset□

21. Qualitative Analysis with Floorplan
21
Author-collected RGB-D Dataset (in SNU)□

22. Quantitative Analysis with True Data
22
Frame Index
TranslationError[m]RotationError[deg]
Rotation error
causes failure
Average rotation
error is ~0.2 deg
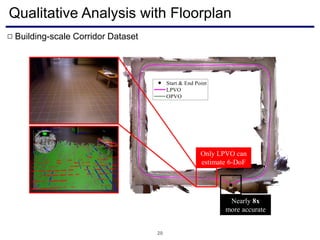
On average, 5x
more accurate
15 Hz @ 10 FPS

23. Problems in Previous LPVO
23
Visually Sparse Indoor Environments
A single line and plane is the theoretical minimal sampling for rotation.□
LPVO sometimes fails when there are insufficient structural regularities.□

24. Proposed Drift-free Rotation Estimation
24
Single Line
Single Plane
Great Circle of
the Single Line
Gaussian Sphere
Normal Vector of
the Great Circle
Surface Normal Vector
of the Single Plane
Single Line & Plane with RANSAC□
 Minimum Geometric Requirement: a Single Line and Plane

25. Multiple Lines Refinement
25
Orthogonal Distance Error Metric□
Cost Function for Refinement□
 We refine the initial rotation estimate from RANSAC for consistency.
 Orthogonal distance is only a function of the remaining orientation angle.

26. Overview of the Proposed Method
26
SLPME (Single Line and Plane Manhattan Estimation)□
RGB Image Line Detection
Depth Image
Single Line & Plane RANSAC
Single Plane
Multiple Lines Refinement
Published in CVPR 2018

27. Qualitative Experiment Results
27
ICL-NUIM Dataset□

28. Quantitative Experiment Results
28
Comparison of the Average Rotation Error (degrees)□
(a) Living Room 0
VP1
VP3
VP2
x
Y
Z
VP1
VP3
VP2
x
Y
Z
Y
VP3
VP2
x
VP1
Z
Frame 1478Frame 196 Frame 931
(b) Office Room 1
x
Y
Z
Y
x Z
Frame 918Frame 160 Frame 530
VP1
VP3
VP2
VP1
VP3
VP2
VP1
VP3
VP2
YZ
x
(a)
(b)

29. Qualitative Experiment Results
29
TUM RGB-D Dataset□
 The proposed method shows consistent line & plane clustering results.

30. Extension from VO to SLAM
30
Development of Simple & Linear SLAM Approach□
 SLAM as A Linear Least Squares Given the Rotation
 SLAM is a High Dimensional Nonlinear Problem
Effectiveness of the Prior Rotation Information
Odometry Initialization Optimum
Torus
Carlone, Luca, et al. "Initialization techniques for 3D SLAM: a survey on rotation estimation and its use in pose graph
optimization." Robotics and Automation (ICRA), 2015 IEEE International Conference on. IEEE, 2015.
 Planar Features in Low-Texture Indoor Environments

31. Our Solution
31
An Orthogonal Plane Detection Method in Structured Environments□
A New, Linear Kalman Filter SLAM Formulation□
Evaluation and Application to Augmented Reality (AR)□
Linear RGB-D SLAM (L-SLAM) with a Global Planar Map
Will be published in ECCV 2018

32. Pipeline of the Proposed SLAM
32
L-SLAM (Linear SLAM in Planar Environments)□
LPVO
L-SLAM
Depth
Linear
SLAM
within
Kalman
Filter
RGB
Point Detection & Tracking
Point
Cloud
Line
Detection
Surface
Normals
Vanishing
Directions
Orthogonal Plane Detection & Tracking
Drift-Free
Rotation
Tracking
Translation
Estimation

33. Orthogonal Plane Detection
33
The Plane Model in RANSAC□
Detected Planes Overlaid on the RGB Image
: The Measured Disparity
: The Normalized Image Coordinates𝑢, 𝑣

34. Linear SLAM Formulation in KF
34
KF State Vector Definition□
 State Vector in Linear KF
 3-DoF Camera Translation
 1-D Distance (Offset) of the Plane
 3-DoF rotational motion is PERFECTLY compensated by LPVO.
 Camera, map position are expressed in global Manhattan map frame.

35. Linear SLAM Formulation in KF
35
Propagation Step (Predict) with LPVO□
 Process Model with LPVO
where ,
 Only 3-DoF camera translation is propagated with LPVO method.
 A constant position model is used in 1-D map position (& alignment).

36. Linear SLAM Formulation in KF
36
Correction Step (Update) with Orthogonal Planes□
 Measurement Model
where
 Observation model is nothing but a distance from the orthogonal plane.
 1-D map positions are also updated in linear KF framework.

37. Evaluation Results
37
ICL-NUIM Dataset□

38. Evaluation Results
38
ICL-NUIM Dataset□
Scene 3D Reconstruction of an Office Room

39. Evaluation Resultslr-kt0nof-kt1nof-kt2nof-kt3n

40. Evaluation Results
40
Author-collected RGB-D Dataset (in SNU Building 301)□

41. Evaluation Results
41
Author-collected RGB-D Dataset (in SNU Building 301)□

42. Evaluation Results
42
Author-collected RGB-D Dataset (in SNU Building 302)□
Accumulated 3D Point Cloud in a Long Corridor Sequence

43. Augmented Reality (AR) Application
43
Arbitrary 3D Model (*.3ds)
3D Reconstructed Environment with L-SLAM
International Space Station (ISS)
Experimental Setup□
 We apply L-SLAM to AR for checking the accuracy and applicability.
 3D object is rendered as an image with the Open Scene Graph (OSG).

44. AR Application Results
44

45. “Some” Failure Cases – (1)
45
Plane Correspondence Problem□
 Difficult to distinguish parallel planes that are close
 Plane matching with alignment and offset distance

46. “Some” Failure Cases – (2)
46
Pose Graph Optimization (Loop Detection)□
 Cannot correct a past mis-predicted 6-DoF camera pose
 There is no back-end optimization component (iSAM, g2o)

47. Summary & Conclusion
47
Existing VO methods suffer from rotation estimation error.□
We exploit lines and planes together to estimate drift-free camera
orientation even when only a single plane is visible.
□
It is rotations that make the SLAM problem highly nonlinear.□
Our Linear SLAM is simple and computationally inexpensive.□

48. The End
Thank You for Your Time!

Any Questions?