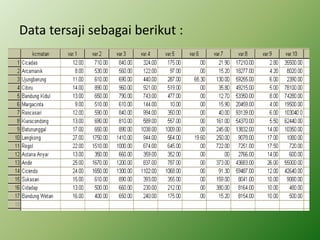
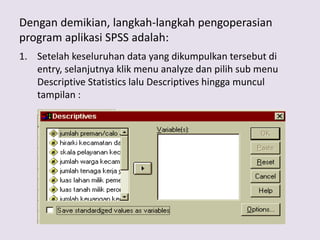
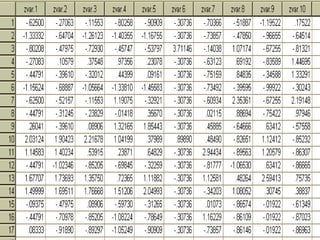
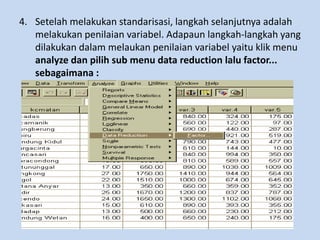
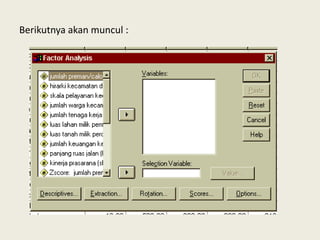
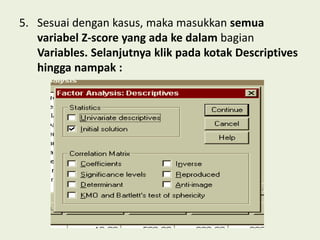
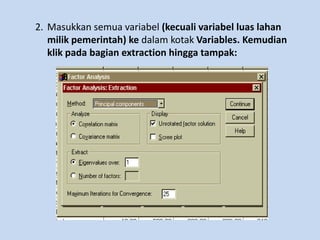
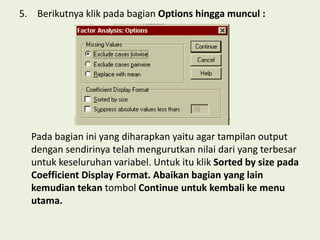
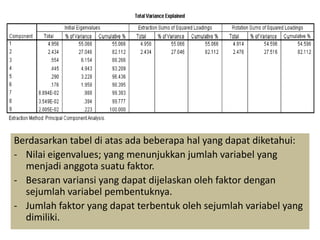
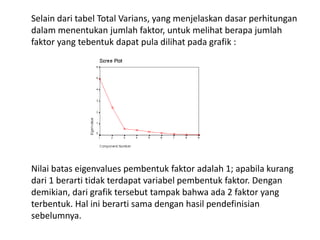
Analisis faktor digunakan untuk mengidentifikasi hubungan antar variabel dan mereduksi jumlah variabel. Metode ini melakukan ekstraksi untuk membentuk satu atau lebih faktor dari variabel awal, diikuti rotasi untuk memperjelas posisi variabel dalam faktor. Kasus contoh menganalisis 10 variabel dari 17 kecamatan untuk merencanakan terminal terpadu di Bandung.