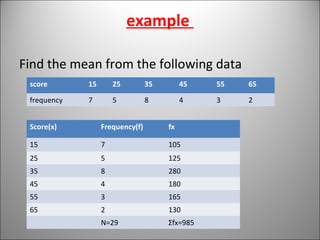
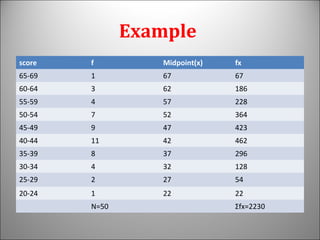
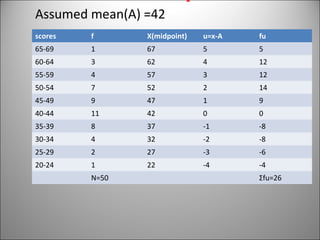
This document discusses the concept and calculation of the mean as a measure of central tendency. It defines the mean as the sum of all values divided by the total number of items. It provides the formula for calculating the mean from both ungrouped and grouped data, using frequency tables. It gives an example of calculating the mean from an ungrouped data set and from a grouped frequency table using midpoints. It also describes a shortcut formula that can be used to calculate the mean from grouped data. Finally, it discusses when the mean is most appropriate to use, noting that it is the most reliable measure when accuracy is needed and when further statistical analysis will be done.

2. PRESENTED BY
GAYATHRI V
MATHEMATICS
MEASURES OF CENTRAL TENDENCY-
MEAN--CONCEPT,METHOD,ANDWHEN
TOUSE

3. MEASURE OF CENTRAL TENDENCY
The tendency of the observations to cluster
round some central value is known as
measure of central tendency.
 A common word used for measure of
central tendency is ‘average’.

4. ARITHEMETIC MEAN
Arithmetic mean is the simplest but most useful
measure of central tendency.
It is nothing but the ‘average’, which we compute
in our high school arithmetic and therefore can
be easily defined as the sum of all values of the
item in a series divided by the number of items. It
is represented by the symbol ‘M’.
Arithmetic mean is sometimes referred to as’the
mean’ or ‘the average’.

5. CALCULATION OF MEAN IN THE CASE OF UNGROUPED DATA
Let X1,X2,……XN be the N observations of the
Sample. Their mean is defined as
M= (X1+X2+……+XN)/N=ΣX/N
Where Σx stands for the sum of values of the item
and N for the total number of items in a series
or group.
Example
i. Calculate the mean from the following data
3,5,10,7,8,12.

6. UNGROUPED FREQUENCY TABLE
Let the values of the variate be X1,X2,….XK and let
f1,f2,…fk be the number of times they occur or the
corresponding frequencies. Then the mean is
calculated by the formula
M=ΣfX/N
Where N is the total of all frequency

7. example
Find the mean from the following data
score 15 25 35 45 55 65
frequency 7 5 8 4 3 2
Score(x) Frequency(f) fx
15 7 105
25 5 125
35 8 280
45 4 180
55 3 165
65 2 130
N=29 Σfx=985

8. Grouped frequency table
In a grouped frequency table the individual
values of the observations falling in a class are
not known. so the mean can not be found out
without making some assumption regarding
the values of observations falling in each class.
The assumption that is usually made is that, all
the observations falling in a class have their
values equal to the midvalue of the class.so the
mean can be found out as in the case of the
ungrouped frequency table.

9. Example
score f Midpoint(x) fx
65-69 1 67 67
60-64 3 62 186
55-59 4 57 228
50-54 7 52 364
45-49 9 47 423
40-44 11 42 462
35-39 8 37 296
30-34 4 32 128
25-29 2 27 54
20-24 1 22 22
N=50 Σfx=2230

10. Shortcut method for mean
Mean for the grouped data can be computed
easily with the help of the following formula
M=A + c*Σfu/N
Where A-assumed mean,
c-class interval,
f-respective frequency of the midvalues of the
class interval,
N-total frequency,and
u=(x-A)/c

11. Assumed mean(A) =42
scores f X(midpoint) u=x-A fu
65-69 1 67 5 5
60-64 3 62 4 12
55-59 4 57 3 12
50-54 7 52 2 14
45-49 9 47 1 9
40-44 11 42 0 0
35-39 8 37 -1 -8
30-34 4 32 -2 -8
25-29 2 27 -3 -6
20-24 1 22 -4 -4
N=50 Σfu=26

12. WHEN TO USE THE MEAN
1. Mean is the most reliable and accurate measure of central
tendency of a distribution in comparison to median and mode. It
has the greatest stability as there are less fluctuations in the mean
of sample drawn from the same population. Therefore , when
reliable and accurate measure of central tendency is needed, we
computed the mean for the given data.
2. Mean can be given an algebraic treatment and is better suited to
further arithmetical computation. Hence it can be easily employed
for he computation of various statistics like standard deviation,
coefficient of correlation,etc.Therefore,when we need to
compute more statistics like these, mean is compued for the
given data.
3. In computation of the mean we give equal weightage to every
item in the series.Therefore it is affected by the value of each item
in that series.

13. Merits
It is rigidly defined
It is easy to understand and simple to
calculate
It depends on the magnitude of all the
observations
It is capable for further algebraic treaatment

14. Demerits
The mean can be an impossible value. For
example, the AM of the number of students
per class in a school may turnout to be a
fraction.
If any observation is missing or its exact
magnitude is not known, the AM can not be
calculated even if its relative position is
known.

15. Thank you