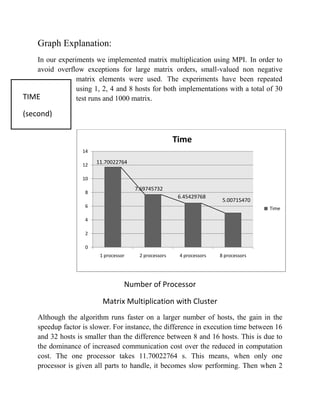
This document discusses four implementations of parallel matrix multiplication on a cluster. It proposes a master-worker model using dynamic block distribution and MPI. Experiments were conducted on a cluster using matrices of size n×n. The performance of the implementations was analyzed and an analytical model was developed that can accurately predict parallel performance. The model considers the matrix multiplication C=A×B with matrices of size n×n on a cluster with p workstations. Experiments showed that increasing the number of nodes from 1 to 8 decreased completion time but with diminishing returns due to communication overhead.

1. Performance of matrix multiplication
on cluster
The matrix multiplication is one of the most important computational
kernels in scientific computing. Consider the matrix multiplication product C =
A×B where A, B, C are matrices of size n×n. We propose four parallel matrix
multiplication implementations on a cluster of workstations. These parallel
implementations are based on the master – worker model using dynamic block
distribution scheme. Experiments are realized using the Message Passing Interface
(MPI) library on a cluster of workstations. Moreover, we propose an analytical
prediction model that can be used to predict the performance metrics of the
implementations on a cluster of workstations. The developed performance model
has been checked and it has been shown that this model is able to predict the
parallel performance accurately.
Performance Model Of The Matrix Implementations:
In this section, we develop an analytical performance model to describe the
computational behavior of the four parallel matrix multiplication implementations
of both kinds cluster. First of all, we consider the matrix multiplication product C =
A×B where the three matrices A, B, and C are dense of size n×n.. The number of
workstations in the cluster is denoted by p and we assume that p is power of 2. The
performance modeling of the four implementations is presented in next subsections
Procedure:
The Program was modified in such as way that each time; it would complete the
multiplication 30 times, and then give out an average. This was done four times,
and each time, the time was measured using 1, 2, 4 and 8 nodes respectively.

2. Graph Explanation:
In our experiments we implemented matrix multiplication using MPI. In order to
avoid overflow exceptions for large matrix orders, small-valued non negative
matrix elements were used. The experiments have been repeated
using 1, 2, 4 and 8 hosts for both implementations with a total of 30
TIME test runs and 1000 matrix.
(second)
Time
14
12
11.70022764
10
7.69745732
8
6.45429768
5.00715470
6 Time
4
2
0
1 processor 2 processors 4 processors 8 processors
Number of Processor
Matrix Multiplication with Cluster
Although the algorithm runs faster on a larger number of hosts, the gain in the
speedup factor is slower. For instance, the difference in execution time between 16
and 32 hosts is smaller than the difference between 8 and 16 hosts. This is due to
the dominance of increased communication cost over the reduced in computation
cost. The one processor takes 11.70022764 s. This means, when only one
processor is given all parts to handle, it becomes slow performing. Then when 2

3. processors used then it take 7.69745732s. We see that it takes less than one
processor time. This shows the improving performance when more nodes are used.
Next 4 takes 6.45429768 s and 8 processors takes 5.00715470s. We see that if we
increase the number of processor then it takes less time. But the 8 processors
performance is not as good as expected, one reason of that can be overhead of
passing messages between processors. From these values, it can be deduced that if
the level is kept constant, and the number of nodes is gradually increased, due to
overhead, the required time may increase as well. But if the number of matrix is
small then the 1 processor will show the better performance because if we take
small matrix then data passing will take more time than multiplication, but the
average performance of 4 processors is better.
Conclusion:
The basic parallel matrix - vector multiplication implementation and a variation are
presented and implemented on a cluster platform. These implementations are based
on cluster platform considered in this paper .Further; we presented the
experimental results of the proposed implementations in the form of performance
graphs. We observed from the results that there is the performance degradation of
the basic implementation. Moreover, from the experimental analysis we identified
the communication cost and the cost of reading of data from disk as the primary
factors affecting performance of the basic parallel matrix vector implementation.
Finally, we have introduced a performance model to analyze the performance of
the proposed implementations on a cluster.