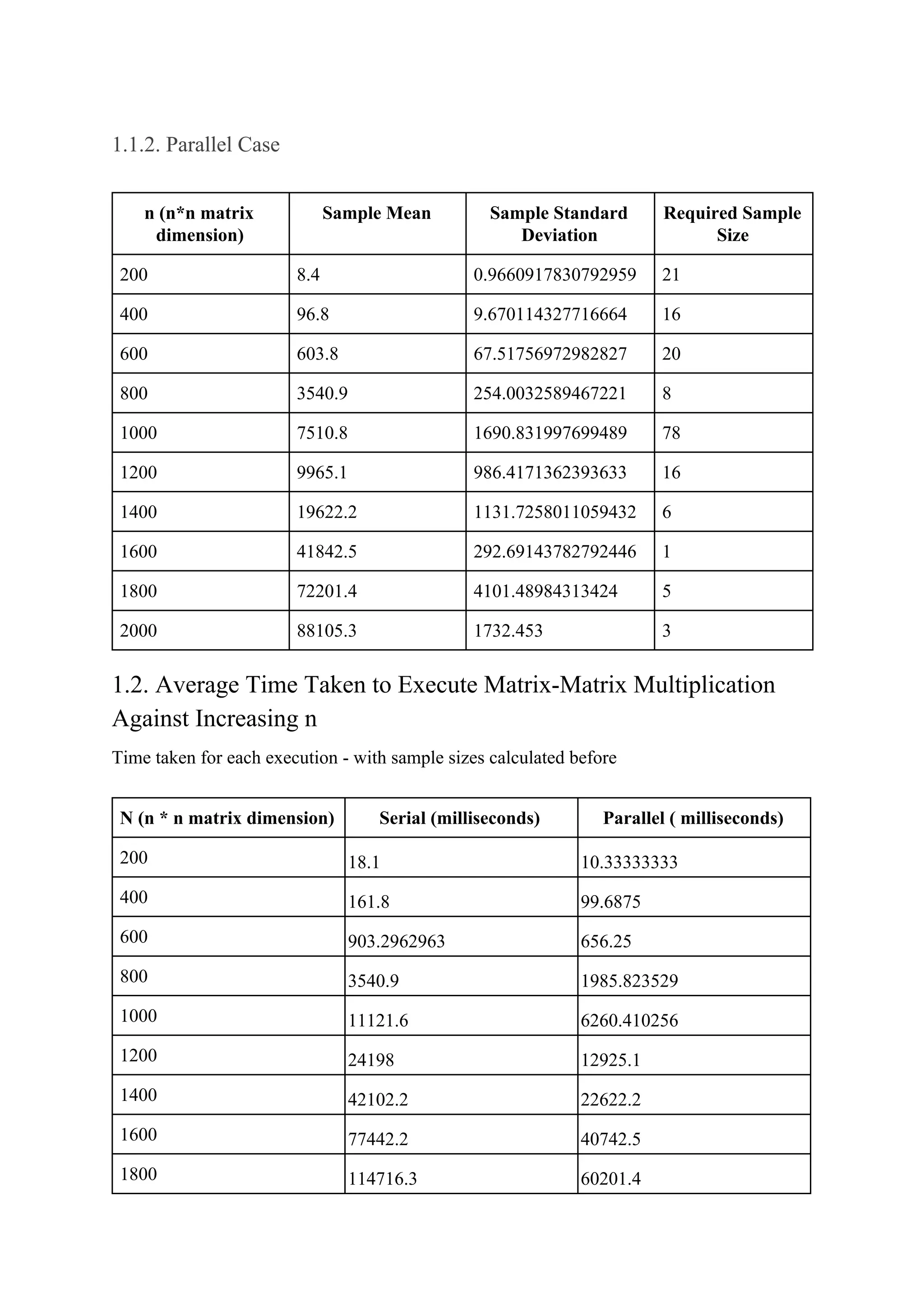
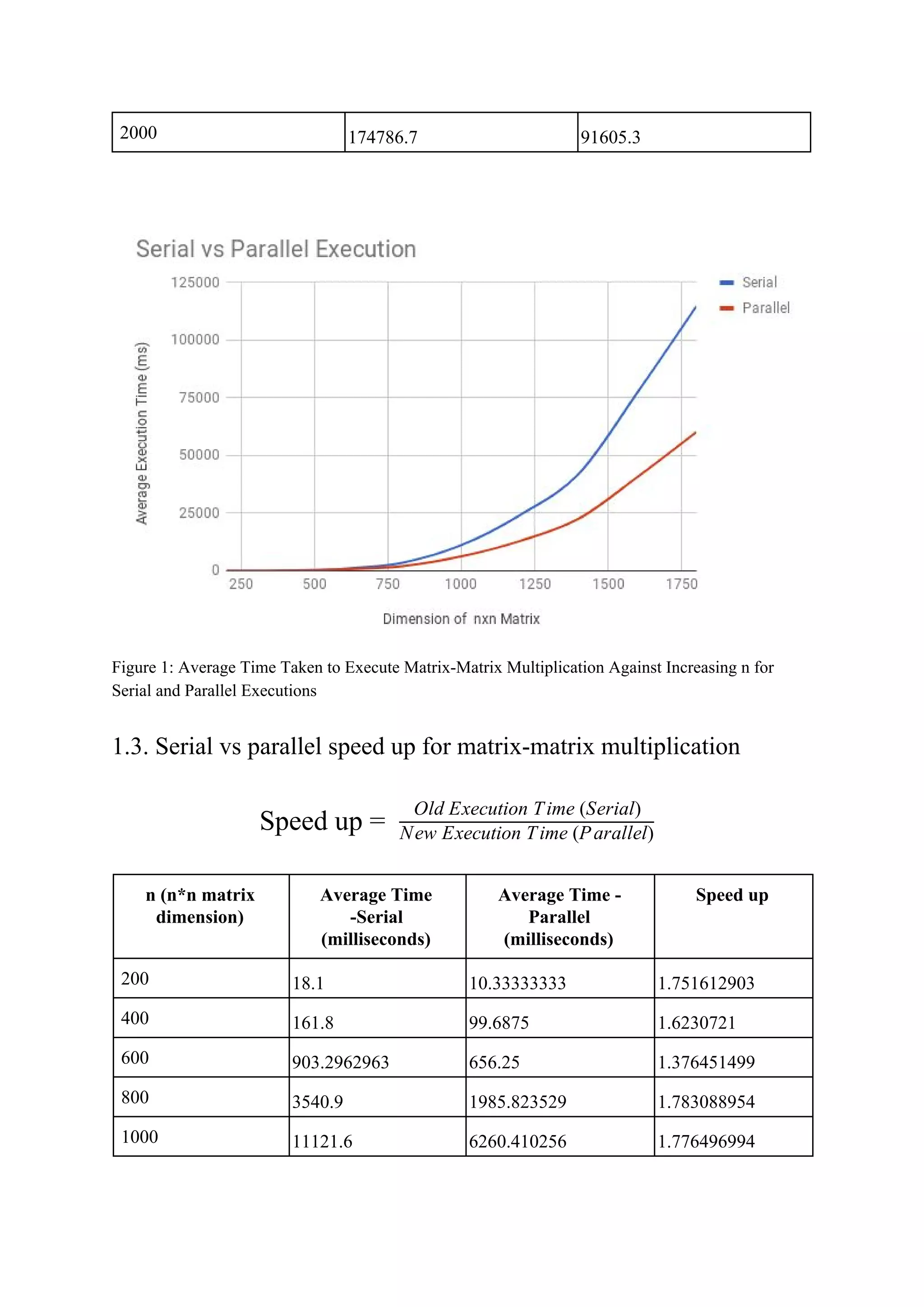
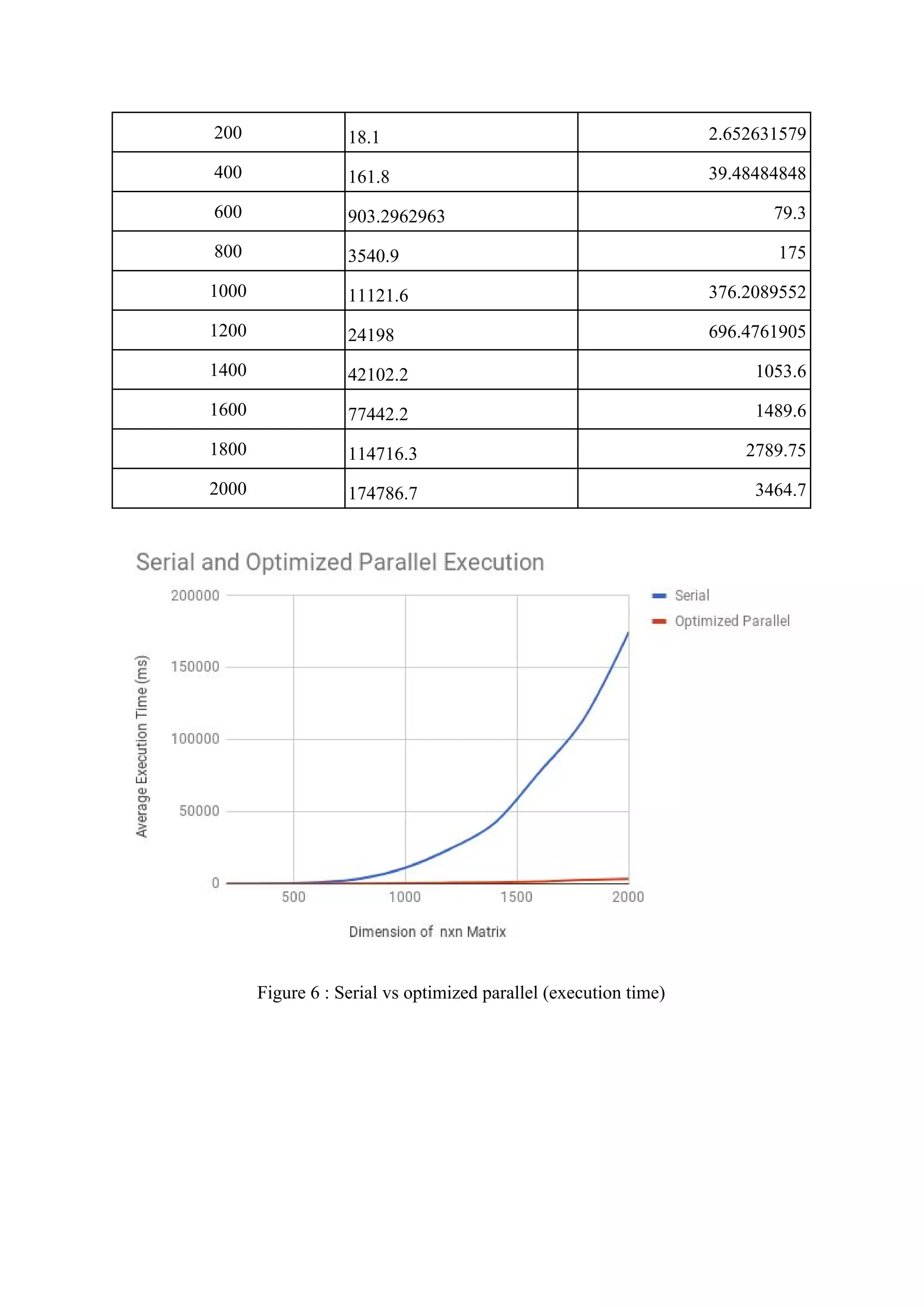
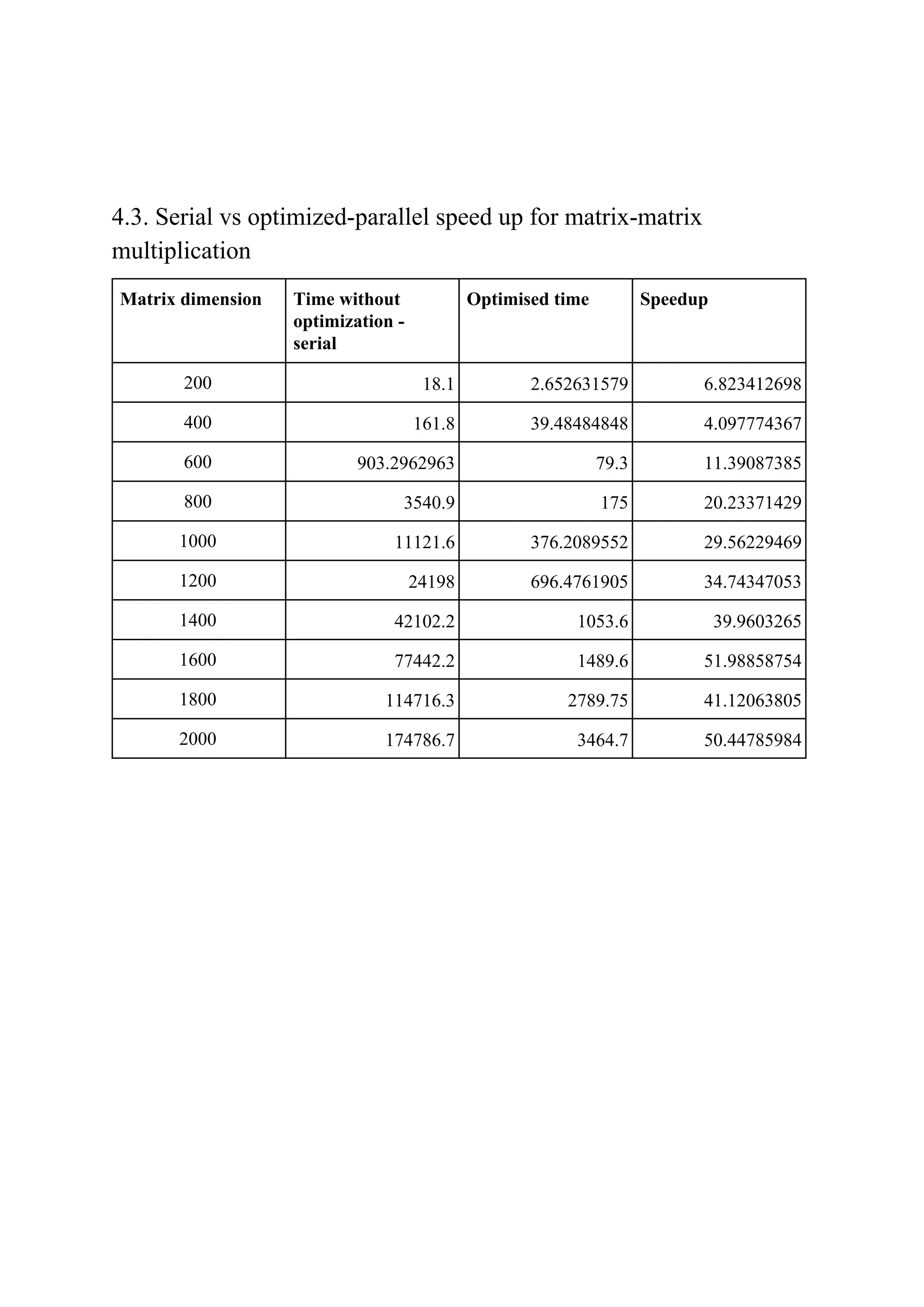
The document consists of a detailed analysis of matrix-matrix multiplication in concurrent programming, outlining various tasks and optimization methods for improving performance. It presents findings on sample sizes, execution times for serial and parallel executions, and speedup comparisons, emphasizing the impact of CPU architecture and threading. The document also discusses observations related to performance optimizations through various techniques, asserting that optimizations significantly enhance speed for larger matrix sizes.

1. CS-4532 Concurrent Programming
Take Home - Lab 4
Team Members:
● S.P.Thewa Hettige – 140623B
● P.D.Geethika - 140176F
Table of Contents
1. Task 4
1.1. Finding the required sample sizes
1.1.1. Serial Case
1.1.2. Parallel Case
1.2. Average Time Taken to Execute Matrix-Matrix Multiplication Against Increasing n
1.4. Serial vs parallel speed up for matrix-matrix multiplication
2. Task 5
2.1. Specification of the Machine
2.2. Justification of the gained speed up, knowing the architecture of the CPU
2.3. Discussions on Observations
3. Task 6
3.1. Optimizing techniques to reduce matrix-matrix multiplication time
3.1.1. Method 1 : Transposing the 2nd matrix
3.1.2. Method 2 : Reduce loop iterations
3.1.3. Method 3 : Blocked (tiled) Matrix multiply (alternative method)
4. Task 8
4.1. Finding Sample Sizes for Parallel Optimization Case
4.2. Average Time Taken to Execute Matrix-Matrix Multiplication Against Increasing n
4.3. Parallel vs optimized-parallel speed up for matrix-matrix multiplication
4.4. Discussion and observation
4.4.1. Observation 1
4.4.2. Observation 2
4.4.3. Observation 3

2. 1. Task 4
1.1. Finding the required sample sizes
We used sample size of 10 to calculate sample mean and standard deviation. Then these
values are used to find the required sample sizes with an accuracy of 5% and 95% confidence
interval using the following equation.
z = 1.960
s = Sample Standard Deviation
r = Required Accuracy
m = Sample Mean
n = Required Sample Size
1.1.1. Serial Case
n (n*n matrix
dimension)
Sample Mean Sample Standard
Deviation
Required
Sample Size
200 18.1 0.31622776601683794 1
400 161.8 4.3410188256265885 2
600 887.1 117.1755093865608 27
800 2597.2 270.043947040724 17
1000 11121.6 407.95538971804257 3
1200 26698 578.0945712712871 1
1400 20283.9 1246.069861604878 6
1600 77442.2 1073.0040695791108 1
1800 114716.3 1100.2491687492127 1
2000 124786.7 1533.995 1

3. 1.1.2. Parallel Case
n (n*n matrix
dimension)
Sample Mean Sample Standard
Deviation
Required Sample
Size
200 8.4 0.9660917830792959 21
400 96.8 9.670114327716664 16
600 603.8 67.51756972982827 20
800 3540.9 254.0032589467221 8
1000 7510.8 1690.831997699489 78
1200 9965.1 986.4171362393633 16
1400 19622.2 1131.7258011059432 6
1600 41842.5 292.69143782792446 1
1800 72201.4 4101.48984313424 5
2000 88105.3 1732.453 3
1.2. Average Time Taken to Execute Matrix-Matrix Multiplication
Against Increasing n
Time taken for each execution - with sample sizes calculated before
N (n * n matrix dimension) Serial (milliseconds) Parallel ( milliseconds)
200 18.1 10.33333333
400 161.8 99.6875
600 903.2962963 656.25
800 3540.9 1985.823529
1000 11121.6 6260.410256
1200 24198 12925.1
1400 42102.2 22622.2
1600 77442.2 40742.5
1800 114716.3 60201.4

4. 2000 174786.7 91605.3
Figure 1: Average Time Taken to Execute Matrix-Matrix Multiplication Against Increasing n for
Serial and Parallel Executions
1.3. Serial vs parallel speed up for matrix-matrix multiplication
Speed up =
Old Execution Time (Serial)
New Execution Time (Parallel)
n (n*n matrix
dimension)
Average Time
-Serial
(milliseconds)
Average Time -
Parallel
(milliseconds)
Speed up
200 18.1 10.33333333 1.751612903
400 161.8 99.6875 1.6230721
600 903.2962963 656.25 1.376451499
800 3540.9 1985.823529 1.783088954
1000 11121.6 6260.410256 1.776496994

5. 1200 24198 12925.1 1.872171202
1400 42102.2 22622.2 1.861101042
1600 77442.2 40742.5 1.900771921
1800 114716.3 60201.4 1.905542064
2000 174786.7 91605.3 1.908041347
Figure 2 : Speedup for sequential vs parallel matrix-matrix multiplications against increasing
n
2. Task 5
2.1. Specification of the Machine
CPU model Intel(R) Core(TM) i3-4005U CPU @ 1.70GHz
Number of cores 2
Number of hardware-level threads 4

6. Cache hierarchy L1d cache - 32K
L1i cache - 32K
L2 cache - 256K
L3 cache - 3072K
RAM 4 mb
2.2. Justification of the gained speed up, knowing the architecture of
the CPU
When analysing the speed up curve of serial over parallel, an increase in speedup can be
observed. There are minor variations in the speed up against increasing N. Reasons for this
behavior can be described as below.
The CPU used in this experiment has 2 cores and 4 threads. In sequential multiplication, the
process only utilizes one thread and sequentially carry out the multiplication process. But by
using multiple threads to perform multiplication process parallely, it can utilize both cores
with 4 threads to parallel calculation process. This will give a significant speedup over the
sequential multiplication.
Even though there are 4 threads in the given CPU architecture we cannot experience a 4 time
speed up. But it is clear that underlying CPU is influences the processing times.
In parallel multiplication we experience a less speed up than the ideal speed up since, the
CPU has to,
● Initialize and terminate threads
● Switch between threads
● Write to shared resources
● Divide workload accordingly to threads
Therefore, it takes quite a bit of time, hence 4 times speedup is not achieved here.
2.3. Discussions on Observations
Figure 1 shows the average times taken for matrix-matrix multiplications for both serial and
Parallel cases. As we all know, the matrix-matrix multiplication takes a time complexity of
O(n​​3​
) and with increasing n, the time taken for processing increases exponentially.
Observation 1:​
With the increasing n, the sequential processing time increases exponentially, where the
parallel processing time increase is relatively low.

7. Even though, the computer used for this experiment has 2 cores and 4 threads, in serial
multiplication, it will only utilize one core and one thread. Because of this reason, when n is
increasing, the number of calculations required increases and the time grows exponentially.
But unlike in the sequential process, in parallel multiplication, this workload is divided
among the 4 threads in the computer, and performs relatively faster.
Observation 2:
When n is low, execution times in both sequential and parallel implementations , are almost
identical.
Serial process performs as well as the parallel process when the workload is relatively low.
The reason for this is, the parallel multiplication tries to divide the small workload available,
among threads and this consumes quite a bit time to initiate and terminate threads, where it
makes the parallel process no different from the serial one.
But as n increases parallel case shows a significant improvement over the serial case. As
depicted in figure 2, the speedup is comparatively low when n is low. parallel multiplication
does not perform significantly faster when n is small, due to switching of threads and
processing, whereas serial multiplication may perform with a similar speed when n is small,
due to the small number of calculations.
But parallel performs better with a higher n, as the workload gets managed amongst threads
for parallel processing.
2.3.1. Observation 3​ :
Slight Unexpected Flutters in the speed up against increasing n is observed
These are negligible fluctuations but these might occur due to few reasons such as threading,
underlying CPU processes or even cache misses.
But overall, the gradual increase in the speed up of the computation is observed in the figure
2.

8. 3. Task 6
3.1. Optimizing techniques to reduce matrix-matrix multiplication
time
Below mentioned methods can be used to optimize matrix matrix multiplication
3.1.1. Method 1 : Transposing the 2nd matrix
In general, the matrices are stored in row major order. When multiplying two matrices A and
B, A will be accessed in row major order and B will be accessed in column major order. It
takes more time to access a matrix in column major order. This happens because when the
matrix is in a row major order, accessing in column major order requires to load all the row
major arrays and access one element per each.
Therefore, in order to reduce the overhead matrix B is transposed, so that we have to load
row major matrices that means only two arrays.
Figure 3: transposing second matrix
3.1.2. Method 2 : Reduce loop iterations
We can reduce the number of loop iterations and reduce jump operations in our code. Since
jump operations produce a considerable amount of overhead, we have loaded more than one
number in one iteration.

9. Figure 4 : reduce loop iterations
3.1.3. Method 3 : Blocked (tiled) Matrix multiply (alternative method)
Large matrices might not fit in to the memory. Therefore the large matrix is broken to smaller
pieces or smaller chunks which are called blocks such that they can be moved easily in to the
memory. Block size must be carefully .Given below is an block matrix multiplication in
action.

10. Figure 5 : block matrix multiplication
Image source : www.sdsc.edu/~allans/cs260/lectures/matmul.ppt
4. Task 8
Execution time after optimization in task 6
4.1. Finding Sample Sizes for Parallel Optimization Case
n (n*n matrix
dimension)
Sample Mean Sample Standard
Deviation
Required
Sample Size
200 2.4 0.8432740427115678 190
400 24.7 3.591656999213594 33
600 79.3 2.9078437983419185 3
800 175 2.8284271247461903 1
1000 453.7 94.09221245376497 67
1200 725.8 84.06716891206037 21
1400 1053.6 12.139924949429375 1
1600 1489.6 7.351492667781452 1
1800 2208.6 188.93632084205868 12
2000 2634.7 94.675 2
4.2. Average Time Taken to Execute Matrix-Matrix Multiplication
Against Increasing n
Matrix dimension Time without optimization
- serial
Optimised time

11. 200 18.1 2.652631579
400 161.8 39.48484848
600 903.2962963 79.3
800 3540.9 175
1000 11121.6 376.2089552
1200 24198 696.4761905
1400 42102.2 1053.6
1600 77442.2 1489.6
1800 114716.3 2789.75
2000 174786.7 3464.7
Figure 6 : Serial vs optimized parallel (execution time)

12. 4.3. Serial vs optimized-parallel speed up for matrix-matrix
multiplication
Matrix dimension Time without
optimization -
serial
Optimised time Speedup
200 18.1 2.652631579 6.823412698
400 161.8 39.48484848 4.097774367
600 903.2962963 79.3 11.39087385
800 3540.9 175 20.23371429
1000 11121.6 376.2089552 29.56229469
1200 24198 696.4761905 34.74347053
1400 42102.2 1053.6 39.9603265
1600 77442.2 1489.6 51.98858754
1800 114716.3 2789.75 41.12063805
2000 174786.7 3464.7 50.44785984

13. Figure 7: speed up serial vs optimized parallel
4.4. Discussion and observation
4.4.1. Observation 1
Serial vs optimized matrix multiplication algorithms shows a gradual improvement in speed
up​. ​When serial multiplication is implemented only one thread will be utilized and it will
sequentially carry out the process. But in the second scenario when we use optimized
threading the program utilizes more threads and cores and carry out the process parallely.
This will provide a significant speedup to the process.
Due to the more work done in parallel as the size of the matrix increases reduces the time to
shift data in and out of the memory. This results in an increased speed up. But due to the
increasing workload serial will not perform well since it only utilizes a single thread
4.4.2. Observation 2
Speed up is not very significant for smaller values but for larger values such as n=1000 it is
Threads take time to initiate schedule and terminate. That time spent becomes more
significant when the problem is too small for multiple threads to handle. As the problem
becomes larger or when n increases since threads do work parallely the time taken to

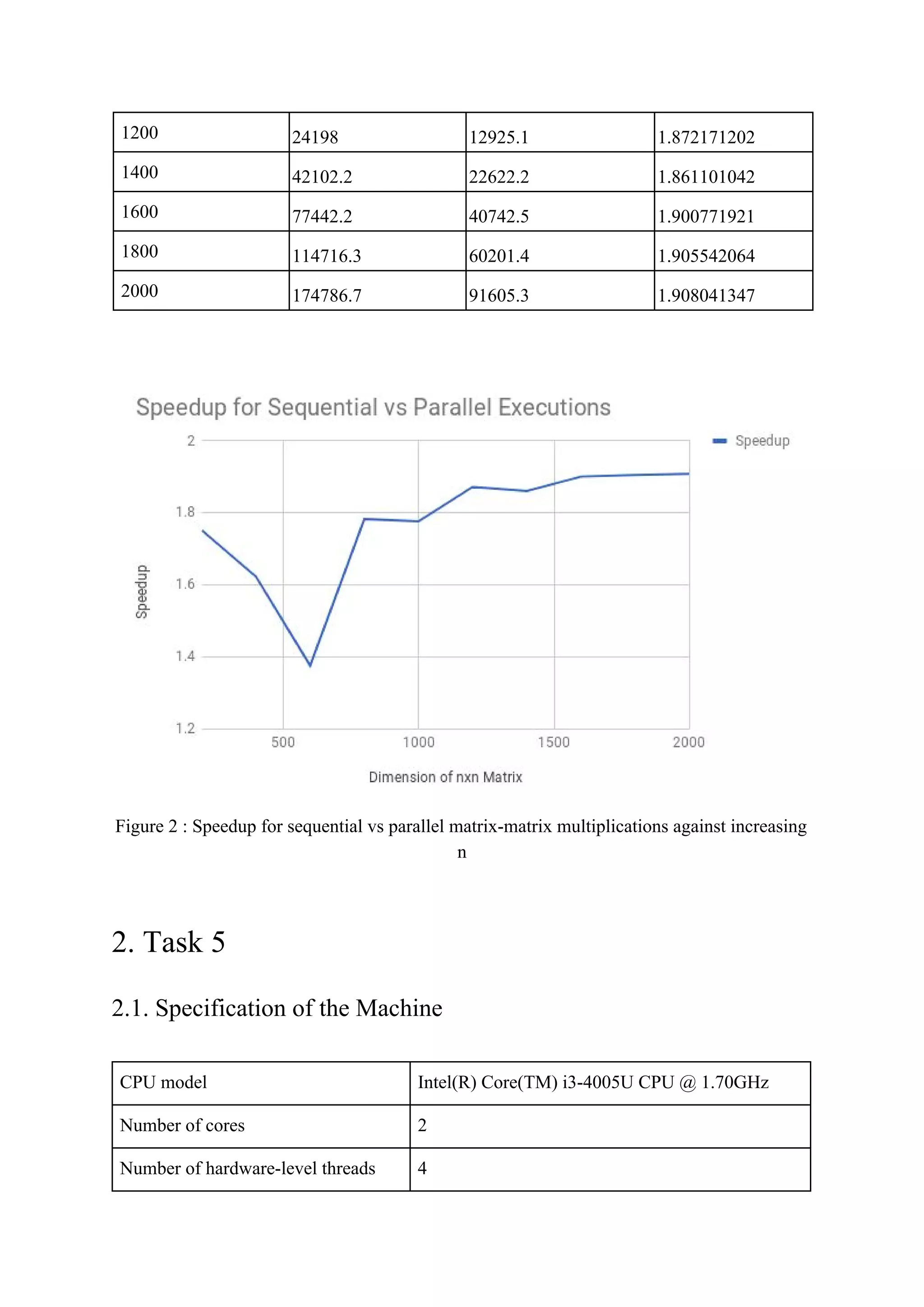
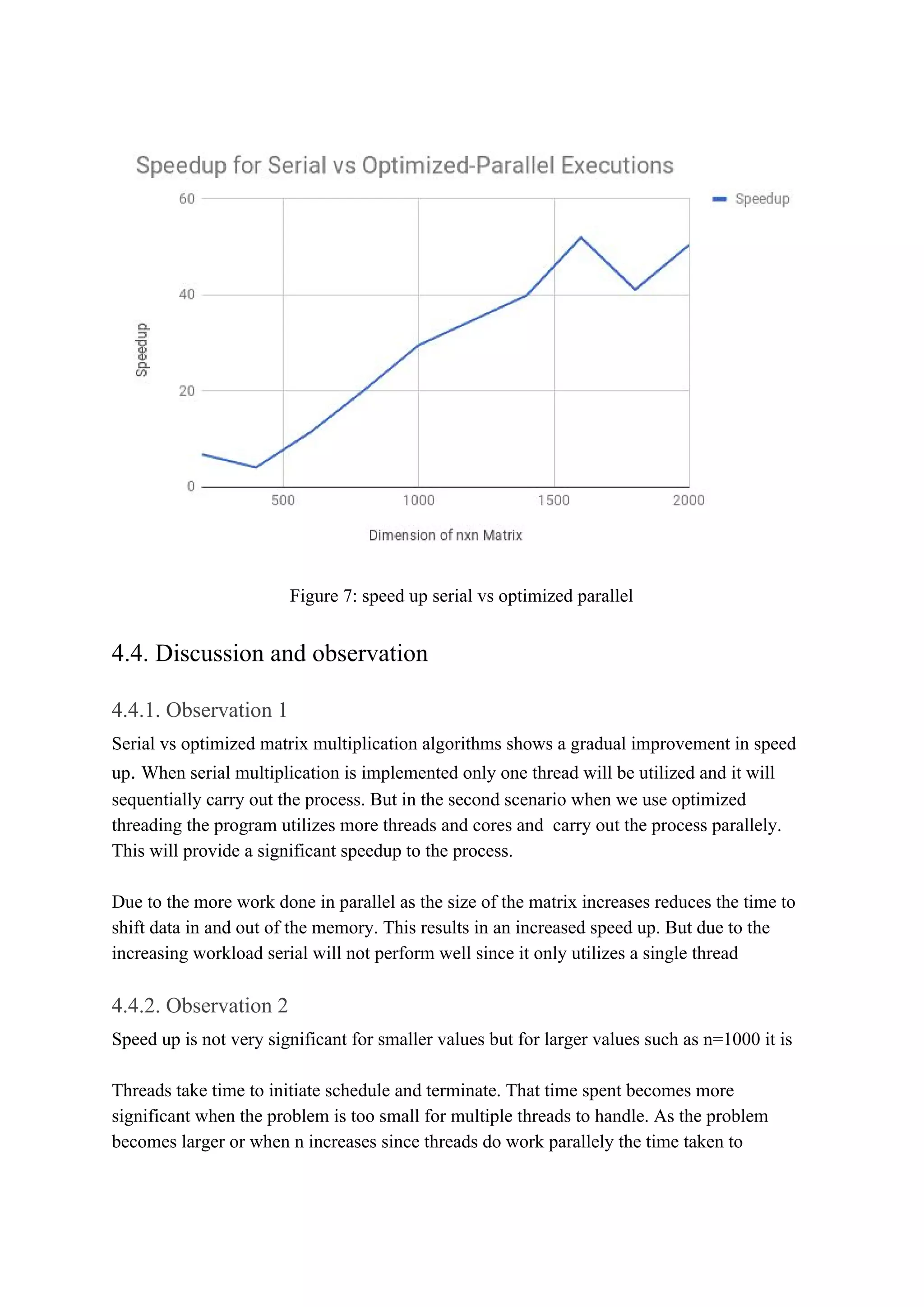
14. schedule becomes less noteworthy. Therefore speedup is very significant when n is larger
than when n is smaller
4.4.3. Observation 3
We expect a gradual increase in speed up against increasing ‘n’
These may occur due to
● Threading
● Underlying CPU processes
● Cache misses
But even though there are minor fluctuations th graph offers a gradual increase in speed up
against increasing n
5. References
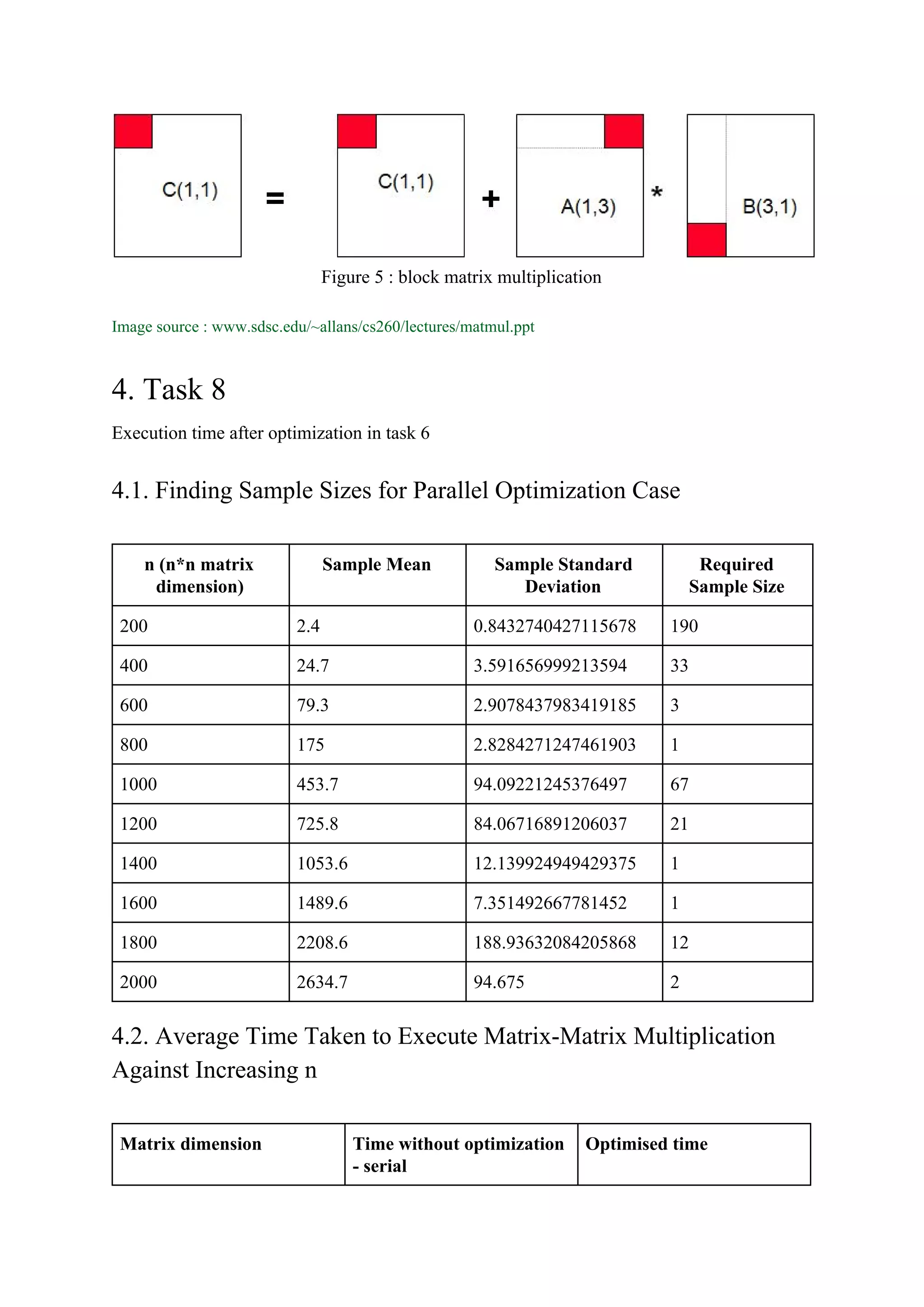
1] Uniprocessor Optimization of Matrix Multiplications and BLAS -
http://web.cs.ucdavis.edu/~bai/ECS231/optmatmul.pdf
2] optimizing for serial processors-
www.sdsc.edu/~allans/cs260/lectures/matmul.ppt