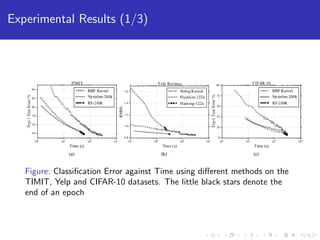
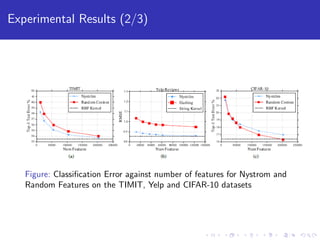
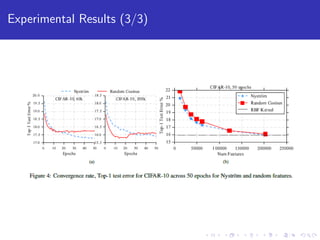
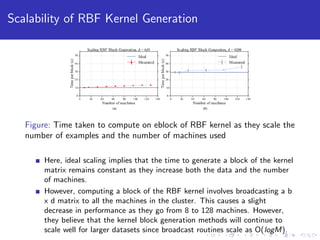
This paper explores using block coordinate descent to scale kernel learning methods to large datasets. It compares exact kernel methods to two approximation techniques, Nystrom and random Fourier features, on speech, text, and image datasets. Experimental results show that Nystrom generally achieves better accuracy than random features but requires more iterations. The paper also analyzes the performance and scalability of computing kernel blocks in a distributed setting.

1. Large Scale Kernel Learning using Block
Coordinate Descent
Shaleen Kumar Gupta, Research Assistant3
Authors:
Stephen Tu1 Rebecca Reolofs1 Shivaram Venkatraman1
Benjamin Recht1,2
1Department of Electrical Engineering and Computer Science
UC Berkeley, Berkeley, CA
2Department of Statistics
UC Berkeley, Berkeley, CA
3Nanyang Technological University, 2016

2. Outline
1 Overview
Introduction
Background
2 Datasets
TIMIT
Yelp Reviews
CIFAR-10
3 Experimental Results
4 Performance and Scalability
5 Conclusion

3. Outline
1 Overview
Introduction
Background
2 Datasets
TIMIT
Yelp Reviews
CIFAR-10
3 Experimental Results
4 Performance and Scalability
5 Conclusion

4. Overview
Kernel methods are a powerful tool in machine learning,
allowing one to discover non-linear structure by mapping data
into a higher dimensional, possibly infinite, feature space.
Problem: They do not scale well.
This paper attempts to exploit distributed computation in
Block CD and present results.
Moreover, the paper attempts to study the performance of
Random Features and Nystrom approximations on three large
datasets from speech (TIMIT), text (Yelp) and image
classification (CIFAR-10) domains.

5. Outline
1 Overview
Introduction
Background
2 Datasets
TIMIT
Yelp Reviews
CIFAR-10
3 Experimental Results
4 Performance and Scalability
5 Conclusion

6. Kernel Methods
https://www.reddit.com/r/MachineLearning/comments/15zrpp/please_explain_support_vector_machines_
svm_like_i/c7rkwce
If our data can’t be separated by a straight line we might need
to use a curvy line.

7. Kernel Methods
https://www.reddit.com/r/MachineLearning/comments/15zrpp/please_explain_support_vector_machines_
svm_like_i/c7rkwce
If our data can’t be separated by a straight line we might need
to use a curvy line.
A straight line in a higher dimensional space can be a curvy
line when projected onto a lower dimensional space.
So what we are really doing is using the kernel to put our data
into a high dimensional space, then finding a hyperplane to
separate the data in that high dimensional space.
This straight line looks like a curvy line when we bring it down
to the lower dimensional space.

8. Kernel Approximation Techniques (1/2)
Kernel Trick: The essence of the kernel-trick is that if you
can describe an algorithm in a certain way – which is using
only inner products – then you never need to actually use the
feature mapping, as long as you can compute the inner
product in the feature space.
While there are many kernel approximation techniques to do
the Kernel Trick, one prominent one is using the RBF Kernel.
We will also analyze two other Kernel approximation
techniques, namely Nystrom Method and Random Features
Technique, in this paper.

9. Kernel Approximation Techniques (2/2)
If we would use all data points, we would map to an RN
dimensional space and have the scaling problems.
Also, we would need to store all kernel values.
Nystrom method says that we don’t need go to the full space
spanned by all N training points, but we can just use a subset.
This will only yield an approximate embedding but if we keep
the number of samples we use the same, the resulting
embedding will be independent of dataset size and we can
basically choose the complexity to suit our problem.
Random feature based methods use an element-wise
approximation of the kernel.

10. Outline
1 Overview
Introduction
Background
2 Datasets
TIMIT
Yelp Reviews
CIFAR-10
3 Experimental Results
4 Performance and Scalability
5 Conclusion

11. TIMIT
Phone classification task was performed on the TIMIT
dataset, which consisted of spoken audio from 462 speakers
The authors applied a Gaussian (RBF) kernel for the Nystrom
and exact methods and used random cosines for the random
feature method.

12. Outline
1 Overview
Introduction
Background
2 Datasets
TIMIT
Yelp Reviews
CIFAR-10
3 Experimental Results
4 Performance and Scalability
5 Conclusion

13. Yelp Reviews
The goal was to predict a rating from one to five stars from
the text of a review.
A usual 80:20 Training:Test split was applied
nltk was used for tokenization and stemming and n-gram
modeling was done with n=3.
For the exact and Nystrom experiments, they apply a linear
kernel.
For random features, they apply a hash kernel using
MurmurHash3 as their hash function.
Since they were predicting ratings for a review, they measured
accuracy by using the root mean square error (RMSE) of the
predicted rating as compared to the actual rating.

14. Outline
1 Overview
Introduction
Background
2 Datasets
TIMIT
Yelp Reviews
CIFAR-10
3 Experimental Results
4 Performance and Scalability
5 Conclusion

15. CIFAR-10
The task was to do image classification of the CIFAR-10
dataset.
The dataset contained 500,000 training images and 4096
features per image.
The authors started with these 4096 features in the dataset as
input and used the RBF kernel for the exact and Nystrom
method and random cosines for the random features method.

16. Experimental Results (1/3)
Figure: Classification Error against Time using different methods on the
TIMIT, Yelp and CIFAR-10 datasets. The little black stars denote the
end of an epoch

17. Experimental Results (2/3)
Figure: Classification Error against number of features for Nystrom and
Random Features on the TIMIT, Yelp and CIFAR-10 datasets

18. Experimental Results (3/3)

19. Performance
Figure: Breakdown of time to compute a single block of coordinate
descent in the first epoch on the TIMIT, Yelp and CIFAR-10 datasets
From the figure, we see that the choice of the kernel
approximation can significantly impact performance since
different kernels take different amounts of time to generate.
For example, the hash random feature used for the Yelp
dataset is much cheaper to compute than the string kernel.
However, computing a block of the RBF kernel is similar in
cost to computing a block of random cosine features.

20. Scalability of RBF Kernel Generation
Figure: Time taken to compute on eblock of RBF kernel as they scale the
number of examples and the number of machines used
Here, ideal scaling implies that the time to generate a block of the kernel
matrix remains constant as they increase both the data and the number
of machines.
However, computing a block of the RBF kernel involves broadcasting a b
x d matrix to all the machines in the cluster. This causes a slight
decrease in performance as they go from 8 to 128 machines. However,
they believe that the kernel block generation methods will continue to
scale well for larger datasets since broadcast routines scale as O(logM).

21. Conclusion
This paper shows that scalable kernel machines are feasible
with distributed computation.
Results suggest that the Nystrom method generally achieves
better statistical accuracy than random features
However, it can require significantly more iterations of
optimization.
On the theoretical side, a limitation of this analysis is that
achieving rates better than gradient descent cannot be hoped.

22. References and Further Reading I
Stephen Tu, Rebecca Roelofs, Shivaram Venkataraman,
Benjamin Recht
Large Scale Kernel Learning using Block Coordinate Descent
February 18, 2016
Tianbao Yang, Yu-feng Li, Mehrdad Mahdavi, Rong Jin,
Zhi-Hua Zhou
Nystrom Method vs Random Fourier Features: A Theoretical
and Empirical Comparison
Advances in Neural Information Processing Systems 25 (NIPS
2012)