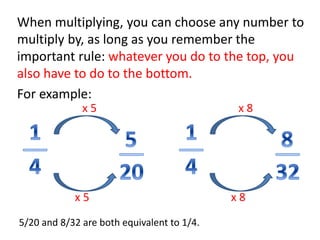
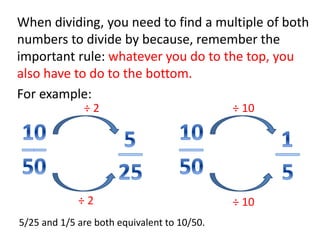
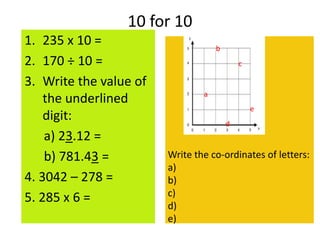
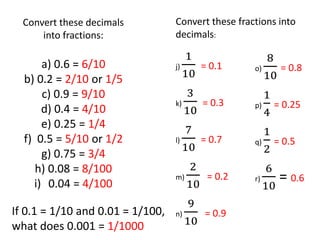
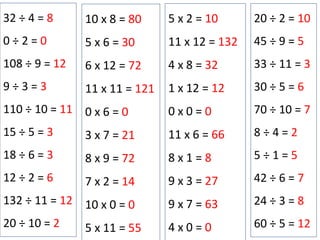
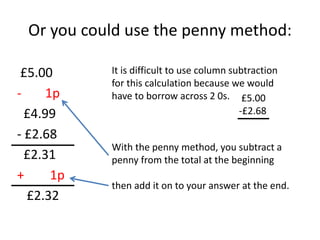
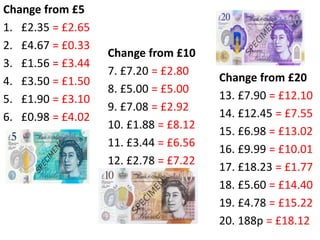
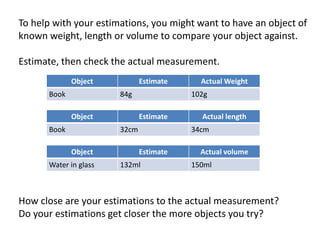
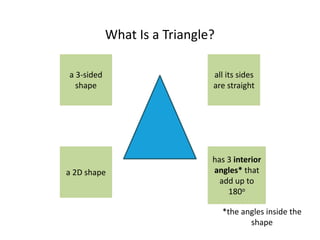
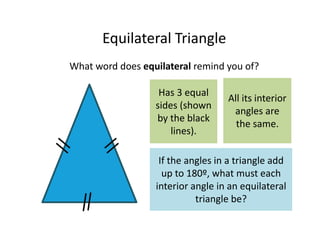
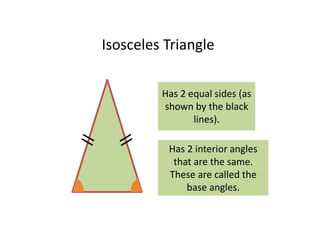
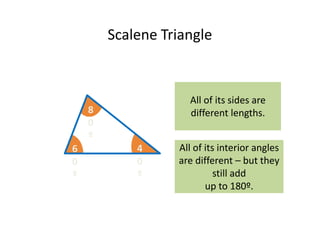
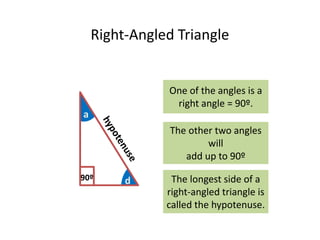
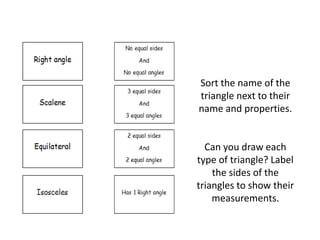
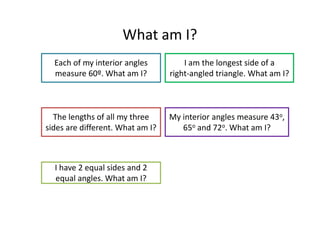
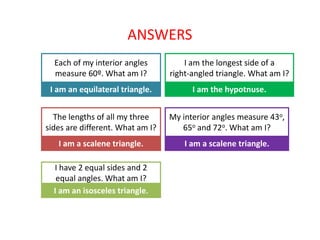
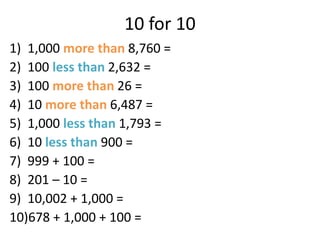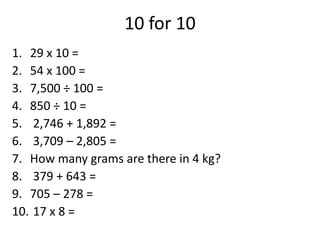This maths home learning document provides practice questions and instructions for students to work on equivalent fractions, decimals, multiplication, division and calculating change from pounds. It includes 10 question maths quizzes with answers provided. Students are asked to convert between fractions and decimals, do multiplication and division calculations, and use methods like the number line or penny method to calculate change from amounts like £5, £10 or £20 after spending.

1. Maths Home Learning
Week beginning 01/06/20

2. 01/06/20
WALT: find equivalent
fractions

3. 10 for 10
1) Use the correct symbol ( < or > or = ) to complete the number sentences:
a) 2,982 ___ 2,890 b) 24.6 ___ 24.60 c) 12.22 ___ 12.29
2) Round 238:
a) To the nearest 10 b) To the nearest 100 c) To the nearest 1,000
3) 3,753 + 236 =
4) 5,672 – 1,235 =
5) 29 x 9 =
6) 347 x 6 =

4. 10 for 10- ANSWERS
1) Use the correct symbol ( < or > or = ) to complete the number sentences:
a) 2,982 > 2,890 b) 24.6 = 24.60 c) 12.22 < 12.29
2) Round 238:
a) To the nearest 10- 240 b) To the nearest 100- 200 c) To the nearest 1,000- 0
3) 3,753 + 236 = 3,989
4) 5,672 – 1,235 = 4,437
5) 29 x 9 = 261
6) 347 x 6 = 2,082

5. 5 x 6 =
6 x 8 =
6 x 3 =
7 x 6 =
11 x 6 =
4 x 6 =
2 x 6 =
6 x 6 =
6 x 9 =
12 x 6 =
10 x 6 =
6 x 4 =
3 x 6 =
6 x 6 =
6 x 11 =
6 x 5 =
6 x 7 =
9 x 6 =
6 x 2 =
10 x 6 =
8 x 6 =
6 x 12 =
48 ÷ 6 =
12 ÷ 6 =
54 ÷ 6 =
42 ÷ 6 =
60 ÷ 6 =
18 ÷ 6 =
30 ÷ 6 =
72 ÷ 6 =
24 ÷ 6 =
36 ÷ 6 =
66 ÷ 6 =

6. 5 x 6 = 30
6 x 8 = 48
6 x 3 = 18
7 x 6 = 42
11 x 6 = 66
4 x 6 = 24
2 x 6 = 12
6 x 6 = 36
6 x 9 = 54
12 x 6 = 72
10 x 6 = 60
6 x 4 = 24
3 x 6 = 18
6 x 6 = 36
6 x 11 = 66
6 x 5 = 30
6 x 7 = 42
9 x 6 = 54
6 x 2 = 12
10 x 6 = 60
8 x 6 = 48
6 x 12 = 72
48 ÷ 6 = 8
12 ÷ 6 = 2
54 ÷ 6 = 9
42 ÷ 6 = 7
60 ÷ 6 = 10
18 ÷ 6 = 3
30 ÷ 6 = 5
72 ÷ 6 = 12
24 ÷ 6 = 4
36 ÷ 6 = 6
66 ÷ 6 = 11

7. Look at this fraction wall. Can you see any fractions that are equivalent in
size? Fractions are equivalent when they line up. For example, 1/2 lines up
perfectly with 2/4- they are equivalent fractions.

8. Fractions are a quantity that is not a whole number.
They are more than 0, but sometimes less than
one.
All of the slices or
8
8
slices = 1
whole pizza.
One slice of this pizza would be
1
8
of the pizza (or 1 out of 8).
What would be another way of
writing
4
8
of the pizza?

9. Equivalent fractions can be found by multiplying
or dividing the numerator and the denominator.
There’s one really important rule: whatever you
do to the top, you also have to do to the bottom.

10. When multiplying, you can choose any number to
multiply by, as long as you remember the
important rule: whatever you do to the top, you
also have to do to the bottom.
For example:
x 5
x 5
x 8
x 8
5/20 and 8/32 are both equivalent to 1/4.

11. When dividing, you need to find a multiple of both
numbers to divide by because, remember the
important rule: whatever you do to the top, you
also have to do to the bottom.
For example:
÷ 2
5/25 and 1/5 are both equivalent to 10/50.
÷ 2
÷ 10
÷ 10

12. Work out what the denominator has been multiplied or divided
by to find the numerator for the equivalent fraction.
EXTRA CHALLENGE- How many more equivalent fractions can you find?

13. Answers

14. 02/06/20
WALT: recognise
decimal/fraction equivalents

15. 10 for 10
1. 235 x 10 =
2. 170 ÷ 10 =
3. Write the value of
the underlined
digit:
a) 23.12 =
b) 781.43 =
4. 3042 – 278 =
5. 285 x 6 =
a
b
c
d
e
Write the co-ordinates of letters:
a)
b)
c)
d)
e)

16. Answers
1. 235 x 10 = 2,350
2. 170 ÷ 10 = 17
3. Write the value of
the underlined digit:
a) 23.12 = 3 or 3 ones
b) 781.43 = 0.03 or 3
hundredths
4. 3042 – 278 = 2,764
5. 285 x 6 = 1,710
a
b
c
d
e
Write the co-
ordinates of letters:
a) (1,2)
b) (2,5)
c) (4,4)
d) (3,0)
e) (5,1)

17. 5 x 7 =
7 x 8 =
7 x 3 =
7 x 7 =
11 x 7 =
4 x 7 =
2 x 7 =
7 x 6 =
7 x 9 =
12 x 7 =
10 x 7 =
7 x 4 =
3 x 7 =
6 x 7 =
7x 11 =
7 x 5 =
7 x 7 =
9 x 7 =
7 x 2 =
10 x 7 =
8 x 7 =
7 x 12 =
49 ÷ 7 =
14 ÷ 7 =
56 ÷ 7 =
42 ÷ 7 =
84 ÷ 7 =
21 ÷ 7 =
35 ÷ 7 =
77 ÷ 7 =
28 ÷ 7 =
70 ÷ 7 =
63 ÷ 7 =

18. 5 x 7 = 35
7 x 8 = 56
7 x 3 = 21
7 x 7 = 49
11 x 7 = 77
4 x 7 = 28
2 x 7 = 14
7 x 6 = 42
7 x 9 = 63
12 x 7 = 84
10 x 7 = 70
7 x 4 = 28
3 x 7 = 21
6 x 7 = 42
7 x 11 = 77
7 x 5 = 35
7 x 7 = 49
9 x 7 = 63
7 x 2 = 14
10 x 7 = 70
8 x 7 = 56
7 x 12 = 84
49 ÷ 7 = 7
14 ÷ 7 = 2
56 ÷ 7 = 8
42 ÷ 7 = 6
84 ÷ 7 = 12
21 ÷ 7 = 3
35 ÷ 7 = 5
77 ÷ 7 = 11
28 ÷ 7 = 4
70 ÷ 7 = 10
63 ÷ 7 = 9

19. 1/4 = 0.25 1/2 = 0.5 3/4 = 0.75
1/10 = 0.1 1/100 = 0.01
2/10 = 1/5 = 0.2 2/100 = 1/50 = 0.02
3/10 = 0.3 3/100 = 0.03
If 1/10 is equivalent to 0.1, what is 6/10 as a decimal?
If 0.2 is equivalent to 2/10, what is 0.8 as a fraction?
If 0.03 is equivalent t0 3/100, what is 0.07 as a fraction?

20. 1/4 = 0.25 1/2 = 0.5 3/4 = 0.75
1/10 = 0.1 1/100 = 0.01
2/10 = 1/5 = 0.2 2/100 = 1/50 = 0.02
3/10 = 0.3 3/100 = 0.03
If 1/10 is equivalent to 0.1, what is 6/10 as a decimal? 0.6
If 0.2 is equivalent to 2/10, what is 0.8 as a fraction? 8/10
If 0.03 is equivalent to 3/100, what is 0.07 as a fraction? 7/100

21. Convert these decimals
into fractions:
a) 0.6 =
b) 0.2 =
c) 0.9 =
d) 0.4 =
e) 0.25 =
f) 0.5 =
g) 0.75 =
h) 0.08 =
i) 0.04 =
Convert these fractions into
decimals:
j)
1
10
k)
3
10
l)
7
10
m)
2
10
n)
9
10
o)
8
10
p)
1
4
q)
1
2
r)
6
10
If 0.1 = 1/10 and 0.01 =
1/100, what does 0.001 = ?

22. Convert these decimals
into fractions:
a) 0.6 = 6/10
b) 0.2 = 2/10 or 1/5
c) 0.9 = 9/10
d) 0.4 = 4/10
e) 0.25 = 1/4
f) 0.5 = 5/10 or 1/2
g) 0.75 = 3/4
h) 0.08 = 8/100
i) 0.04 = 4/100
Convert these fractions into
decimals:
j)
1
10
= 0.1
k)
3
10
= 0.3
l)
7
10
= 0.7
m)
2
10
= 0.2
n)
9
10
= 0.9
o)
8
10
= 0.8
p)
1
4
= 0.25
q)
1
2
= 0.5
r)
6
10
= 0.6
If 0.1 = 1/10 and 0.01 = 1/100,
what does 0.001 = 1/1000

23. 03/06/20
WALT: calculate change

24. 10 x 8 =
5 x 6 =
6 x 12 =
11 x 11 =
0 x 6 =
3 x 7 =
8 x 9 =
7 x 2 =
10 x 0 =
5 x 11 =
32 ÷ 4 =
0 ÷ 2 =
108 ÷ 9 =
9 ÷ 3 =
110 ÷ 10 =
15 ÷ 5 =
18 ÷ 6 =
12 ÷ 2 =
132 ÷ 11 =
20 ÷ 10 =
5 x 2 =
11 x 12 =
4 x 8 =
1 x 12 =
0 x 0 =
11 x 6 =
8 x 1 =
9 x 3 =
9 x 7 =
4 x 0 =
20 ÷ 2 =
45 ÷ 9 =
33 ÷ 11 =
30 ÷ 5 =
70 ÷ 10 =
8 ÷ 4 =
5 ÷ 1 =
42 ÷ 6 =
24 ÷ 3 =
60 ÷ 5 =

25. 10 x 8 = 80
5 x 6 = 30
6 x 12 = 72
11 x 11 = 121
0 x 6 = 0
3 x 7 = 21
8 x 9 = 72
7 x 2 = 14
10 x 0 = 0
5 x 11 = 55
32 ÷ 4 = 8
0 ÷ 2 = 0
108 ÷ 9 = 12
9 ÷ 3 = 3
110 ÷ 10 = 11
15 ÷ 5 = 3
18 ÷ 6 = 3
12 ÷ 2 = 6
132 ÷ 11 = 12
20 ÷ 10 = 2
5 x 2 = 10
11 x 12 = 132
4 x 8 = 32
1 x 12 = 12
0 x 0 = 0
11 x 6 = 66
8 x 1 = 8
9 x 3 = 27
9 x 7 = 63
4 x 0 = 0
20 ÷ 2 = 10
45 ÷ 9 = 5
33 ÷ 11 = 3
30 ÷ 5 = 6
70 ÷ 10 = 7
8 ÷ 4 = 2
5 ÷ 1 = 5
42 ÷ 6 = 7
24 ÷ 3 = 8
60 ÷ 5 = 12

26. To find change, you can use the
number line method:
£1.43
Put the amount spent
at the beginning of the
number line
£5.00
Put the amount you had
to begin with at the end
of the number line
£1.50
+ 7p
£2.00
+ 50p + £3.00
Jump in small steps until you get from the amount spent to the total.
Then you need to add up the jumps- 7p + 50p + £3.00 = £3.57
So £5.00 - £1.43 = £3.37

27. Or you could use the penny method:
£5.00
- 1p
£4.99
- £2.68
£2.31
+ 1p
£2.32
It is difficult to use column subtraction
for this calculation because we would
have to borrow across 2 0s.
With the penny method, you subtract a
penny from the total at the beginning
then add it on to your answer at the end.
£5.00
-£2.68

28. Use your preferred method to find the change
from £5, £10 and £20 on the following slide.
You could use a mixture of both methods, or try
borrowing across the 0s if you feel confident.

29. Change from £5
1. £2.35
2. £4.67
3. £1.56
4. £3.50
5. £1.90
6. £0.98
Change from £10
7. £7.20
8. £5.00
9. £7.08
10. £1.88
11. £3.44
12. £2.78
Change from £20
13. £7.90
14. £12.45
15. £6.98
16. £9.99
17. £18.23
18. £5.60
19. £4.78
20. 188p

30. Change from £5
1. £2.35 = £2.65
2. £4.67 = £0.33
3. £1.56 = £3.44
4. £3.50 = £1.50
5. £1.90 = £3.10
6. £0.98 = £4.02
Change from £10
7. £7.20 = £2.80
8. £5.00 = £5.00
9. £7.08 = £2.92
10. £1.88 = £8.12
11. £3.44 = £6.56
12. £2.78 = £7.22
Change from £20
13. £7.90 = £12.10
14. £12.45 = £7.55
15. £6.98 = £13.02
16. £9.99 = £10.01
17. £18.23 = £1.77
18. £5.60 = £14.40
19. £4.78 = £15.22
20. 188p = £18.12

31. 04/06/20
WALT: estimate measures

32. 10 for 10
1) 1,000 more than 8,760 =
2) 100 less than 2,632 =
3) 100 more than 26 =
4) 10 more than 6,487 =
5) 1,000 less than 1,793 =
6) 10 less than 900 =
7) 999 + 100 =
8) 201 – 10 =
9) 10,002 + 1,000 =
10)678 + 1,000 + 100 =

33. ANSWERS
1) 1,000 more than 8,760 = 9,760
2) 100 less than 2,632 = 2,532
3) 100 more than 26 = 126
4) 10 more than 6,487 = 6,497
5) 1,000 less than 1,793 = 793
6) 10 less than 900 = 890
7) 999 + 100 = 1,099
8) 201 – 10 = 191
9) 10,002 + 1,000 = 11,002
10)678 + 1,000 + 100 = 1,778

34. 144 ÷ 12 =
42 ÷ 7 =
12 ÷ 6 =
25 ÷ 5 =
33 ÷ 3 =
84 ÷ 7 =
16 ÷ 8 =
54 ÷ 9 =
18 ÷ 2 =
24 ÷ 12 =
121 ÷ 11 =
9 x 9 =
4 x 1 =
12 x 8 =
8 x 8 =
0 x 7 =
5 x 9 =
3 x 2 =
11 x 11 =
10 x 12 =
7 x 6 =
0 x 3 =
7 x 5 =
3 x 4 =
3 x 8 =
12 x 4 =
8 x 3 =
0 x 11 =
12 x 2 =
10 x 9 =
5 x 6 =
12 x 7 =
6 x 4 =

35. 144 ÷ 12 = 12
42 ÷ 7 = 6
12 ÷ 6 = 2
25 ÷ 5 = 5
33 ÷ 3 = 11
84 ÷ 7 = 12
16 ÷ 8 = 2
54 ÷ 9 = 6
18 ÷ 2 = 9
24 ÷ 12 = 2
121 ÷ 11 = 11
9 x 9 = 81
4 x 1 = 4
12 x 8 = 96
8 x 8 = 64
0 x 7 = 0
5 x 9 = 45
3 x 2 = 6
11 x 11 = 121
10 x 12 = 120
7 x 6 = 42
0 x 3 = 0
7 x 5 = 35
3 x 4 = 12
3 x 8 = 24
12 x 4 = 48
8 x 3 = 24
0 x 11 = 0
12 x 2 = 24
10 x 9 = 90
5 x 6 = 30
12 x 7 = 84
6 x 4 = 24

36. How many different
units of measure
can you think of?

37. Liquids can be measured in millilitres (ml) and litres (l)
Distance can be measured in metres (m), kilometres
(km) or miles
Length/width/height can be measured in centimetres
(cm) or metres (m)
Weight can be measured in grams (g) and kilograms (kg)

38. Estimating
An estimate is an educated guess, using the information you
already have.
You can estimate the
• weight (g/kg) (if you have a set of scales)
or
• length (cm/m) (if you have a ruler or tape measure)
or
• volume (ml/l) (if you have a measuring jug)
of different objects around your house.

39. Object Estimate Actual Weight
Book 84g 102g
Object Estimate Actual length
Book 32cm 34cm
Object Estimate Actual volume
Water in glass 132ml 150ml
To help with your estimations, you might want to have an object of
known weight, length or volume to compare your object against.
Estimate, then check the actual measurement.
How close are your estimations to the actual measurement?
Do your estimations get closer the more objects you try?

40. 05/06/20
WALT: identify different types
of triangle

41. 10 for 10
1. 29 x 10 =
2. 54 x 100 =
3. 7,500 ÷ 100 =
4. 850 ÷ 10 =
5. 2,746 + 1,892 =
6. 3,709 – 2,805 =
7. How many grams are there in 4 kg?
8. 379 + 643 =
9. 705 – 278 =
10. 17 x 8 =

42. ANSWERS
1. 29 x 10 = 290
2. 54 x 100 = 5,400
3. 7,500 ÷ 100 = 75
4. 850 ÷ 10 = 85
5. 2,746 + 1,892 = 4,638
6. 3,709 – 2,805 = 904
7. How many grams are there in 4 kg? 4,000g
8. 379 + 643 = 1,022
9. 705 – 278 = 427
10. 17 x 8 = 136

43. 5 x 11 =
8 x 11 =
11 x 3 =
7 x 11 =
11 x 11 =
4 x 11 =
2 x 11 =
11 x 6 =
11 x 9 =
12 x 11 =
11 x 10 =
11 x 4 =
3 x 11 =
6 x 11 =
11 x 11 =
11 x 5 =
11 x 7 =
11 x 9 =
11 x 2 =
10 x 11 =
11 x 8 =
11 x 12 =
110 ÷ 11 =
121 ÷ 11 =
55 ÷ 11 =
44 ÷ 11 =
88 ÷ 11 =
22 ÷ 11 =
33 ÷ 11 =
77 ÷ 11 =
132 ÷ 11 =
99 ÷ 11 =
66 ÷ 11 =

44. 5 x 11 = 55
8 x 11 = 88
11 x 3 = 33
7 x 11 = 77
11 x 11 = 121
4 x 11 = 44
2 x 11 = 22
11 x 6 = 66
11 x 9 = 99
12 x 11 = 132
11 x 10 = 110
11 x 4 = 44
3 x 11 = 33
6 x 11 = 66
11 x 11 = 121
11 x 5 = 55
11 x 7 = 77
11 x 9 = 99
11 x 2 = 22
10 x 11 = 110
11 x 8 = 88
11 x 12 = 132
110 ÷ 11 = 10
121 ÷ 11 = 11
55 ÷ 11 = 5
44 ÷ 11 = 4
88 ÷ 11 = 8
22 ÷ 11 = 2
33 ÷ 11 = 3
77 ÷ 11 = 7
132 ÷ 11 = 12
99 ÷ 11 = 9
66 ÷ 11 = 6

45. What Is a Triangle?
a 2D shape
a 3-sided
shape
all its sides
are straight
has 3 interior
angles* that
add up to
180o
*the angles inside the
shape

46. Equilateral Triangle
What word does equilateral remind you of?
Has 3 equal
sides (shown
by the black
lines).
All its interior
angles are
the same.
If the angles in a triangle add
up to 180º, what must each
interior angle in an equilateral
triangle be?

47. Isosceles Triangle
Has 2 equal sides (as
shown by the black
lines).
Has 2 interior angles
that are the same.
These are called the
base angles.

48. Scalene Triangle
All of its sides are
different lengths.
All of its interior angles
are different – but they
still add
up to 180º.
8
0
º
4
0
º
6
0
º

49. Right-Angled Triangle
The other two angles
will
add up to 90º
a
d
One of the angles is a
right angle = 90º.
90º The longest side of a
right-angled triangle is
called the hypotenuse.

50. Sort the name of the
triangle next to their
name and properties.
Can you draw each
type of triangle? Label
the sides of the
triangles to show their
measurements.

51. What am I?
Each of my interior angles
measure 60º. What am I?
I am the longest side of a
right-angled triangle. What am I?
The lengths of all my three
sides are different. What am I?
My interior angles measure 43o,
65o and 72o. What am I?
I have 2 equal sides and 2
equal angles. What am I?

52. ANSWERS
Each of my interior angles
measure 60º. What am I?
I am an equilateral triangle.
I am the longest side of a
right-angled triangle. What am I?
I am the hypotnuse.
The lengths of all my three
sides are different. What am I?
I am a scalene triangle.
My interior angles measure 43o,
65o and 72o. What am I?
I am a scalene triangle.
I have 2 equal sides and 2
equal angles. What am I?
I am an isosceles triangle.