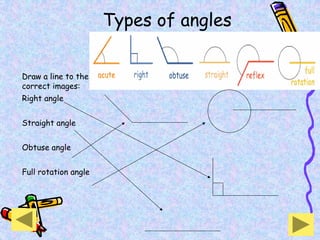
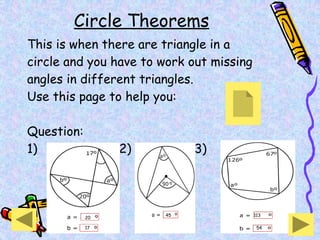
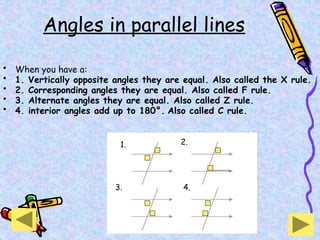
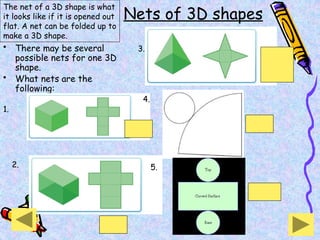
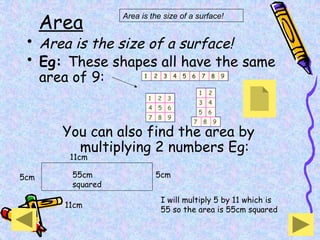
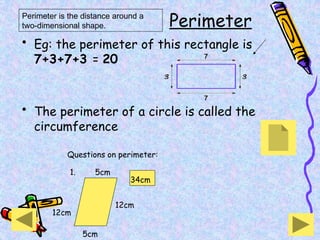
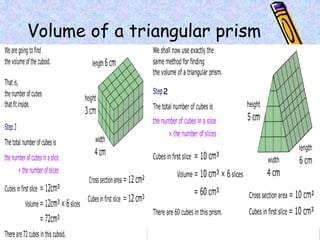
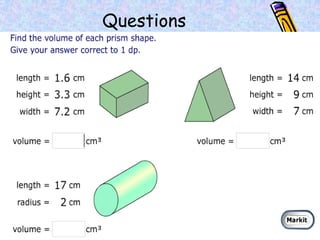
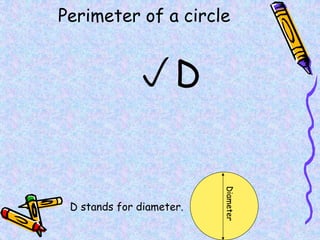
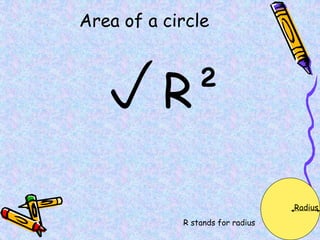
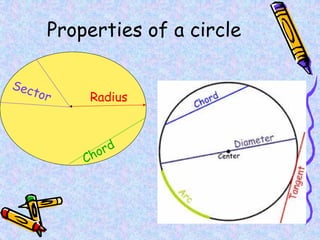
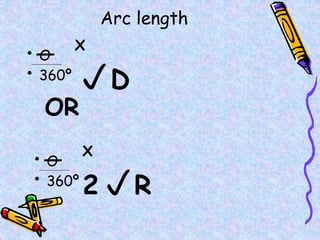
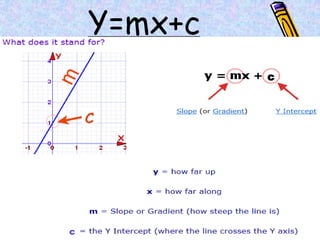
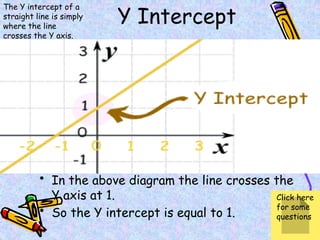
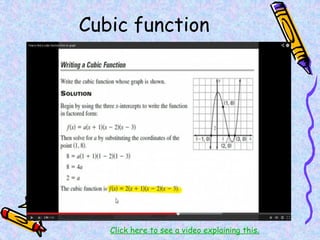
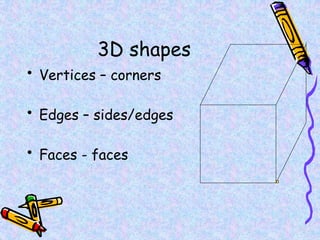
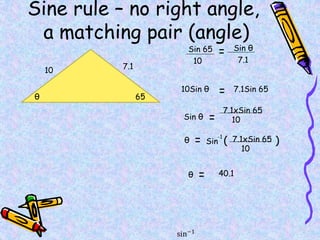
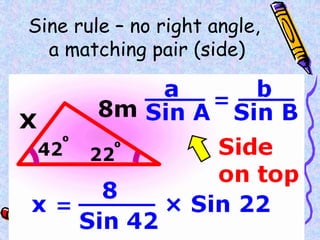
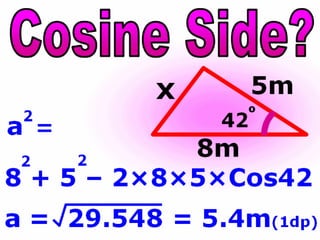
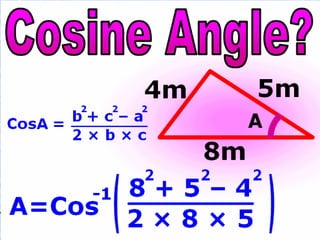
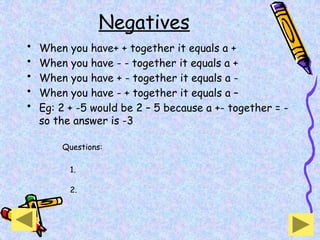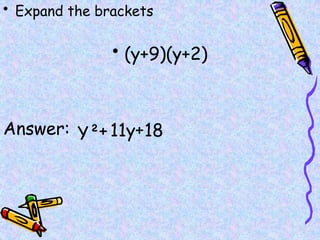The document covers various mathematical concepts including square numbers, factors, prime numbers, substitution in algebra, nth terms, mean, median, mode, angles, 3D shapes, area, volume, and probability. It provides definitions, examples, and questions to reinforce learning, making it a comprehensive revision guide. Additionally, it includes topics on the metric system, symmetry, and procedures for calculations involving fractions, decimals, and indices.

1. MATHS REVISION

3. Square numbers
• A square number is when you times a number by
its self Eg 4 squared is 4 x 4 which equals 16.
• Use the table below which shows you all the
square numbers

4. Multiples
• Multiples are really just times tables.
• EG: The multiples of 2 are all the numbers in the 2 times
table:
2, 4, 6, 8, 10 and so on.
• The multiples of 5 are all the numbers in the 5 times table:
5, 10, 15, 20, 25 and so on.
Questions: list 5 of these times
tables
1. Four Times Tables
2. Six Times Tables
3. Seven Times Tables
4. Eight Times Tables
5. Twelve Times Tables
4, 8, 12, 16, 20
6, 12, 18, 24, 30
7, 14, 21, 28, 35
8, 16, 24, 32, 40
12, 24, 36, 48, 60

5. Common Big and Small Numbers
Name Number
Trillion 1,000,000,000,000
Billion 1,000,000,000
Million 1,000,000
Thousand 1,000
Hundred 100
ten 10
Unit 1 1
Tenth 0.1
Hundredth 0.01
Thousandth 0.001
Millionth 0.000 001
Billionth 0.000 000 001

6. Factors
• Factors are numbers that divide exactly
into another number.
• EG: The factors of 12, are 1, 2, 3, 4, 6
and 12
Questions:
1. The factors of 1 are
2. The factors of 2 are
3. The factors of 3 are
4. The factors of 4 are
5. The factors of 5 are
8. The factors of 8 are
9. The factors of 9 are
10. The factors of 10 are
6. The factors of 6 are
7. The factors of 7 are
Answers:
1. One
2. One and two
3. One and three
4. One, two and four
5. One and five
6. One, two, three and six
7. One and seven
8. One, two, four and eight
9. One, three and nine
10. One, two, five and ten

7. Prime Numbers
A Prime Number is a number that can be divided
evenly only by 1, or itself.
And it must be a whole number greater than 1.
Example: 5 can only be divided evenly by 1 or 5, so
it is a prime number.
but 6 can be divided evenly by 1, 2, 3 and 6 so it is
NOT a prime number
Questions:
1. Is the number 18 prime? no 5. Is the number 97 prime? yes
2. Is the number 45 prime? no
3. Is the number 79 prime? yes
4. Is the number 90 prime? no

9. Algebra - Substitution
"Substitute" means to put in the place of another.
• Substitution
• In Algebra "Substitution" means putting numbers
where the letters are:
• If you had x5+12= and you knew that x=2 and if a
number and letter together means you’ve got to
times them then you know all you have to do is
5x2+12= and then you can work out the answer in
this case the answer is 22

10. Nth term
• Nth term is when you replace some
letters for numbers
• Use this page to help you:

11. Finding the nth term
• 8,11,14
• The common difference is 3, so it must be
related to the 3 times table (3n)
• The 3 times table is 3, 6, 9, ...
The sequence is 8, 11, 14, ....
• Every term in the sequence is 5 more than
the corresponding term in the 3 times
table, so the nth term is 3n + 5.

12. Finding the nth term for a
quadratic sequence

13. Finding nth term of a
sequence
Eg. 2,5,10,17,26
2. Not a constant
difference so we have to
fine out the second
difference.
3.This second difference
is constant at 2.This
means the nth term will
start with n².
4. But if you do replace 1 for n it will be 1² which is 1 but the first number is 2
the difference between 2 and 1 is 1.
If you replace 2 for n it will be 2² which is 4 but the second number is 5 the
difference between 5 and 4 is 1.
We can see here that it the terms in the sequence are 1 number high each time
so we write the answer as…..
n²+1
1. Find the first
difference.

14. Nth term
2nd
differences:
• 2 = n²
• 4 = 2n²
• 6 = 3n²

16. Mean/Average
• The mean is just the average of the
numbers. It is easy to calculate: add up all
the numbers, then divide by how many
numbers there are.
• Listen to this

17. Median
• The Median is the "middle number"
(in a sorted list of numbers). To find
the Median, place the numbers you
are given in value order and find the
middle number.

18. Mode
• The mode is simply the number which
appears most often. To find the
mode, or modal value, first put the
numbers in order, then count how
many of each number.

19. Range
• The range means you have to take
the small number away from the
bigger number to get the range.

20. Modal group
• If you had a stem and leaf diagram like this for example
• 1/1,2,6 2/4,4,4,5,7,8,9 3/1,6 4/2 5/4,7
• The mode would be the value on the "leaf"
that appears most frequently so in this case
it would be 24.
• However, the modal group would be the
group from the "stem" that has the most
values, so in this case it would focus on the
20's.
• You would write it from the number on the
stem
to the highest in the group, like- 20-29.

21. • Frequency density =
frequency ÷ class width

23. Angles
• Angles are measured in degrees. The sign for degrees is °.
• One whole turn is 360°.
• One quarter turn is 90° or a right angle.
• One half turn is 180° or a straight line.
An angle which is small then 90
Right angle-
Straight angle-
Obtuse angle-
Full rotation angle-
Acute angle-
Is formed by cutting a circle in
quarters. 90
What is:
Half a circle. 180
An angle bigger than 90 but less than 180
A whole circle. 360
Angle

24. Draw a line to the
correct images:
Right angle
Straight angle
Obtuse angle
Full rotation angle
Types of angles

25. Circle Theorems
This is when there are triangle in a
circle and you have to work out missing
angles in different triangles.
Use this page to help you:
Question:
1) 2) 3)
20
17
45 113
54

26. Angles 2
• Angles in a triangle 180

27. Angles in parallel lines
• When you have a:
• 1. Vertically opposite angles they are equal. Also called the X rule.
• 2. Corresponding angles they are equal. Also called F rule.
• 3. Alternate angles they are equal. Also called Z rule.
• 4. interior angles add up to 180°. Also called C rule.
3. 4.
2.
1.

29. Nets of 3D shapes
• There may be several
possible nets for one 3D
shape.
• What nets are the
following:
The net of a 3D shape is what
it looks like if it is opened out
flat. A net can be folded up to
make a 3D shape.
1.
3.
2.
4.
5.
cube
cuboid
Square
based
pyramid
cylinder
cone

30. The Pentagram
• The Pentagram (or Pentangle) is a 5-pointed star.
• Inside a Pentagram is a Pentagon
• You can make a pentagram by first drawing a
pentagon, then extending the edges.
• Or by drawing lines from corner to corner inside
a pentagon

31. Area
• Area is the size of a surface!
• Eg: These shapes all have the same
area of 9:
You can also find the area by
multiplying 2 numbers Eg:
Area is the size of a surface!
11cm
5cm
5cm
11cm
I will multiply 5 by 11 which is
55 so the area is 55cm squared
55cm
squared

32. Perimeter
• Eg: the perimeter of this rectangle is
7+3+7+3 = 20
• The perimeter of a circle is called the
circumference
Perimeter is the distance around a
two-dimensional shape.
Questions on perimeter:
1.
12cm
12cm
5cm
5cm
34cm

34. Rotation
• The distance from the centre to any point on
the shape stays the same. Every point makes a
circle around the centre.
• Here a triangle is rotated around
the point marked with a "+"
"Rotation" means turning around a
centre

35. Metric system
• Liquids= millilitres + litres 1 litre = 1,000
millilitres
• Weight= Grams, Kilograms, Tonnes 1 kilogram =
1,000 grams 1 tonne = 1,000 kilograms
• Length= Millimetres, Centimetres, Metres,
Kilometres 1 centimetre = 10 millimetres 1 metre
= 100 centimetres 1 kilometre = 1000 meters
• Temperature= Celsius, Fahrenheit

36. Symmetry
A 2D shape is symmetrical if a line can be
drawn through it so that either side of the
line looks exactly the same. The line is
called a line of symmetry.
Shape Lines of symmetry
Square 4
Equilateral triangle 3
Parallelogram 0
Isosceles triangle 1
Rectangle 2

37. Negatives
• When you have+ + together it equals a +
• When you have - - together it equals a +
• When you have + - together it equals a -
• When you have - + together it equals a –
• Eg: 2 + -5 would be 2 – 5 because a +- together = -
so the answer is -3
Questions:
2.
1.

38. Money
• You have 10p
How much change will you
get? 7p
3p
change
Answer
4p
6p
change
Answer
How much change
will you get?
1.
2.

39. What is a product?
• The product is the answer you get when you
multiply numbers. For example: If you multiply
two times eight, the product (also know as the
answer) is sixteen.

40. Multiplying decimals 1
• You have to make both the decimal numbers into
whole numbers multiply it by 10, 100, 1000 etc
then do the sum with whole numbers then divided
the answer by the number you multiplied it by.
Don’t forget to do divide twice if you have two
numbers.

41. Multiplying Decimals 2
• 1 x 1 = 1
• 0.75 x 0.75 = 0.5625
• O.5 x 0.5 = 0.25
• 0.25 x 0.25 = 0.0625

42. Multiplying Indices

43. Dividing Indices

44. Bracket Indices

45. Multiplying indices with
different numbers

46. Indices
• Say we had this question 2( x 3 ) I
would have to do 2 times which will
be 2 then we will put that to the side.
Then we will do 2 times 3 which
will be 6 . Then we put the answers
together to get the answer 2 +6 .

48. Adding like fractions

49. Multiplying mixed number
fractions 2
1. Write out the sum
2. Write the mixed number
as an improper fraction
3. Cancel by dividing the top and
bottom number by the number
that equally goes into each
number
4.

50. Adding fractions
6 2
8 4

51. Subtracting fractions
1 3
4 6

52. Multiplying fractions
2 5
3 6

53. Dividing fractions
2 1
3 5

54. simplifying
• Anything times by 0 is 0
• Anything times by 1 is itself
• Multiplying a number by itself is
called squaring

55. Volume of cuboid
2
2

56. Volume of a triangular prism
2

57. Volume of a cylinder
2

58. Questions

59. Pi equals
 3.14



60. Perimeter of a circle
D
D stands for diameter.
Diameter

61. Area of a circle
R²
R stands for radius
Radius

62. Circumference of a circle
D
OR
2R

63. Properties of a circle
Radius
Chord
Sector

64. Arc length
• Θ
• 360º
X
D
OR
X
2R
• Θ
• 360º

65. Congruent
• The word 'Congruent' in maths means
that two or more things are exact
same size and shape. They should slot
together when you place the shapes
together.

66. Y=mx+c
c
C
c

67. Gradient/Slope
• The method to calculate the Gradient
is:
• Divide the change in height by the
change in horizontal distance
• Gradient = Change in Y
• Change in X
Please go to
the next
slide for
some
examples of
this
The Gradient (also
called Slope) of a
straight line shows
how steep a
straight line is.

68. Examples
1. The Gradient of this line
= 3/3= 1. So the Gradient
is equal to 1
2. The Gradient of this line =
4/2 =2. (The line is steeper,
and so the Gradient is
larger)
3. The Gradient of this line =
3/5= 0.6. (The line is less
steep, and so the Gradient
is smaller) Click here
for some
questions

69. Y Intercept
• In the above diagram the line crosses the
Y axis at 1.
• So the Y intercept is equal to 1.
The Y intercept of a
straight line is simply
where the line
crosses the Y axis.
Click here
for some
questions

70. • B-rackets
• I-ndices
• D-ivision
• M-ultiplication
• A-ddition
• S-ubtraction

71. Mixed numbers to
improper fractions
http://www.youtube.com/watch?
v=shpf9krdXQQ

72. Percentage to decimal
• Percent means "per 100", so 50% means 50 per 100, or
simply 50/100.
If you divide 50 by 100 you get 0.5 (a decimal number).
So, to convert from percent to decimal: divide by 100, and
remove the "%" sign.
The Easy Way:
The easy way to divide by 100 is to move the decimal point 2
places to the left, so
From Percent To Decimal
move the decimal point 2 places to the left, and remove the
"%" sign.

73. Cubic function
Click here to see a video explaining this.

74. Reciprocal function
Click here to see a video explaining this.

75. Pythagoras Theorem
• A² + B² = C²
• √c²
A
B
C?
OR

76. Pythagoras Theorem 2
• C² - B² = A²
• √A²
A?
B
C

77. Angles in a triangle
• To figure out the angle inside any shape
your have to do 180º(n-2)
• N stands for the number of sides a shape
has.
• Example:
This shape has 6 sides so 6-2=4.
Then you have to do 180ºx4=720º.
The interior angles add up to 720.
To find each individual angle do
720º / 6 = 120º
OR

78. • See how many triangles can be
formed in the shape. Then times it
by 180º.
• Example:
As you can see we can create 6
triangles from this octagon.
We then do 180ºx6=1080º.
We can do the same for each
individual angle.
1080º/8=135º

79. Cumulative frequency
• N always stands for how many
numbers there are in the sequence.
• Lower quartile - ⅛
• Median - ⅛
• Upper quartile - ⅛
4
2
4
n
N
3n
Mode – Most often
Range – largest – smallest
Median – middle when in order
Mean – Total of added numbers / number of
numbers

80. 3D shapes
• Vertices – corners
• Edges – sides/edges
• Faces - faces

81. Volume
• H x w x l
• H=height
• W=width
• L=length

82. Probability
• I have 2 dice
• 1 has the numbers 2,4,6,8 on
• The other dice has the numbers 2,3,4,5 on
• If I roll both dice and add both number
together. What would the probability be
that I get an even total?
• Green=even
+ 2 4 6 8
2 4 6 8 10
3 5 7 9 11
4 6 8 10 12
5 7 9 11 13
P(Even number)= 8 = 1
16 2

83. • Expand the brackets
• (y+9)(y+2)
Answer: Y²+11y 18

84. • Simplify
• 6y² + 12y
• You have to think of a number
and/or letter that goes into
both 6 and 12. In this case it
will be 6. Then complete the
simplifying.
• Answer : 6y(y+2)

85. Cumulative frecuency-finding the median and
interquartile range for grouped data
• Watch this video

86. Sine rule – no right angle,
a matching pair (angle)
65
10 7.1
θ
Sin 65 Sin θ
10 7.1
=
=
10Sin θ 7.1Sin 65
Sin θ =
7.1xSin 65
10
θ = Sin ( )
7.1xSin 65
10
-1
θ = 40.1

87. Sine rule – no right angle,
a matching pair (side)

88. Cosine rule – no right
angle, no matching pair
• a²= b²+ c² - 2bc Cos A

89. 9km
12km
x
20
A B
C
a
b
c
a²=9²+12²-2 x 9 x 12 x Cos 20
a²= 81 + 144 -2 x 9 x 12 x Cos 20
a²= 225 – 202.974
a²= 22.026
a²=√22.026
a=4.7km

92. Interior angles
•n-2 x 180

93. Exterior angles
•Always add up
to 360˚