This document is an introduction to F.W. Newman's Mathematical Tracts from 1888. It provides an overview of the contents which include discussions on the bases of geometry, primary ideas of spheres and circles, definitions of straight lines and planes, parallel lines, and volumes of pyramids and cones. The first tract focuses on ratios of incommensurable quantities and introduces the concept of variable quantities that increase uniformly to establish ratios. It then discusses primary geometric ideas including spheres, circles, poles, and parallel circles on a sphere. Finally, it defines straight lines as that which connects two points evenly and introduces the concept of a plane.

7. MATHEMATICAL TRACTS
PAET I.
BY
F. W. NEWMAN, M.RA.S.
EMERITUS PROFESSOR OP UNIVERSITY COLLEGE, LONDON
HONORARY FELLOW OF WORCESTER COLLEGE, OXFORD.
Cambridge :
MACMILLAN AND BOWES.
1888
[All Rights reserved.]

9. TKACT I.
ON THE BASES OF GEOMETRY WITH THE
GEOMETRICAL TREATMENT OF J^l.
CONTENTS.
(1) On the Treatment of Ratio between Quantities Incommensurable.
(2) Primary Ideas of the Sphere and Circle. Poles of a Sphere.
(3) Definition and Properties of the Straight Line.
(4) Definition and Properties of the Plane.
(5) Parallel Straight Lines based on the Infinite Area of a Plane Angle.
(6) On the Volume of the Pyramid and Cone.
I. THE RATIO OF INCOMMENSURABLES.
1. IN arithmetic the first ideas of ratio and proportion, and
the laws of
passage from one set of 4 proportionals to another, ought
to be learned, as preliminary to geometry; but in geometry the
doctrine of incommensurables requires a special treatment, unless
the learner be well grounded in the argument of infinite converging
series. Repeating decimals may perhaps suffice. Another, possibly
better
way,
is open by the introduction of VARIABLE quantitu ".
which will here be proposed.
2. Nothing is simpler than to imagine some geometrical quantity
to vary
in shape or size according to some prescribed law. This
must imply at least two quantities varying together. Thus, if an
equilateral triangle change the length of its side, its area a Is..
changes. If the radius of a circle increase or diminish, so does the
length of the circumference. In general two magnitudes X and Y
may vary together: they may
be either the same in kind, " as the
radius and circumference of a circle is each a length; or the two may
be different in kind, say, a length and an area. In general it is a
N,
1

10. 2 VARIABLES WHICH INCREASE UNIFORMLY.
convenient notation to suppose that when X changesto X', Y changes
to r.
3. Again,if X receive successive additions a^ayCg ...#", the cor-responding
additions (ifadditions theybe) to Y are well denoted by
y'i2/*2/3--'Vn- An obvious and simple case, if it occur, will deserve
notice;namely, if the two variables are so regulated,that equality
in the first set of additions (i.e.#^=3^= x3 "
...
=#") induces equality
in the second set; (i.e.y^=yz=y^= ... =yn). The variables X and Y
are then said to increase uniformly. As an obvious illustration,sup-pose
X to be the arc of a circle,and Y the area
of the sector which it bounds, evidentlythen if
the arcs #,,#" are equal increments of the arc X,
the sectors y^yz which are bounded by x^ will
be equal increments of Y. Then the arc X and
the sector Y increase togetheruniformly.
4. We may now establish a theorem highlyconvenient for ap-plication
in geometry, alike whether quantitiesare commensurable
or incommensurable.
THEOREM. "
If X and Y are any two connected variables,which
beginfrom zero together,and increase uniformly; then X varies
proportionablyto Y. In other words, if Y become Y' when X be-comes
X', then X is to X' as Y is to FV
Proof. First,suppose X and X' commensurable, and f a common
measure, or X= m . f (m times f) and X' =
n". We may then sup-pose
X and X' made up by repeatedadditions of f.
Every time
that X has the increment ", Y will receive a uniform increment
which we may call v then Y is alwaysthe same multipleof v that
X is of f; thus the equationX =
mj; impliesY=mv, and X' =
n^
impliesY'=nv. Hence X : X'=m : n= Y : Y'.
Next, when X' is not commensurate with X, yet f is some snh-
multipleof X, such that n% = X, and X' contains f more than "///
times,but less than (m + 1) times ; evidentlywe cannot have
X : X' = Y : F
(when the four magnitudes are presentedto us) unless, as a first
condition,on assuming nv= Y, we find Y' to contain v more than
m times and l"-s than (m+ 1) times: and unless tin's condition were
fulfilled,X and Y would not increase uniformly.We may therefore

11. DISTANCE OR SHORTEST PATH.
assume X9X8 on oppositesides of X', with values
likewise F2F3 on oppositesides of F',with values
Then by the first case we have X : Xz = Y : F2 and X : X3= Y : F3.
But X^-X^j;, and F3" F2=u. Let n perpetuallyincrease,then f
and v perpetuallylessen. Xz and Xz run togetherin X', F2 and
run togetherin Y'. Thus each of the ratios X : Xz and X : X3 falls
into X : X', and each of the ratios F : F2) F : F3 falls into F : )".
Inevitablythen, X : X' = Y : Y', even when these last are incom-mensurate.
Q.E.D.
II. PRIMARY IDEAS OF THE SPHERE AND CIRCLE.
For the convenience of beginners,POSTULATES may be ad van cvd
concerning the straightline and the plane,as well as concerning
parallelstraightlines. But in the second stage of study the whole
topicought to be treated anew from the beginning:a task which is
here assumed.
On Length and Distance.
THEOREM. "
All lengthsare numericallycomparable."To make
this clear,it is simplestto imaginea thread indefinitelythin, flexible
and inextensible. This,if appliedupon any given line,will become an
exact measure of its length;and if any two lines be then measured
by two threads,the threads are directlycomparable,shewing either
that they are equal,or that one is longerthan the other and ln"w
much longer. Hereby we safelyassert the same fact concerning
any two givenlengths.
Obviously,lengthis continuous magnitude:which means, that i
a pointP run alongfrom A to B, the lengthAP passes throw jh ail
magnitudefrom zero to AB.
THEOREM. Any two givenpointsin space may be joinedeither
by one path which is shorter than any other possible,or by si'
equalpathsthan which none other is so short. For of all possible
pathsjoiningthem some must be needlesslylong;yet unless there
is some limit to the shortening,the distance would be nil; the |"
would not be two, but would coincide and become one.
1"2

12. 4 THE SPHERE.
DEF. A shortest path that joinstwo pointsin space gives a
ire of their DISTANCE. The same argument applies,if the two
givenpointsand the line that joinsthem must lie on a given surface;
or again,if two surfaces that do not touch be given,and we speak of
the shortest distance of the two surfaces.
Assume a fixed pointA and a second point S so movable as
always to be at the same distance from it. It will be able to playall
round A : therefore its locus will be a surface enclosingA. The
s""lid mass enclosed is called a SPHERE (Globeor Ball) and A its
( 'KNTRE.
THEOREM. "
Every pointoutside the sphereis furtherfrom the
centre and every pointwithin the sphereis nearer to the centre,than
are the pointson the surface." For if T be an exterior point,every
path joiningT to A must piercethe surface in some point$; there-fore
the path TSA is longerthan SA by the interval TS. Again,if
R be within the sphere,we may imagine an interior sphere whose
surface is at the common distance AR from A. Then 8 being
exterior to the new sphere,SA is longerthan RA ; that is,R within
the sphereof S is nearer to A than is the locus of 8. Q. E. D.
DEF. Two such concentric spheresenclose within their surfaces
a solid called a sphericalshell.
THEOREM. "The two surfaces are equidistant,each from the
other." For if the shortest distance from a pointS to the inner sur-face
is the path SR, symmetry all round shews at once that if from a
second pointS' the shortest path will be S'R',the two distances SR,
S'R' will be equal. Indeed it is not amiss to remark, that if any
sphericalsurface be rigidlyattached to its centre, the entire surface
may glideon its own ground without disturbingits centre, because
th"- distances SA, S'A nowhere change. Hence also we may justly
imagine the sphericalshell to glideon its own ground,while the
centre suffers no displacement,and any shortest path S'R joining
the oppositesides of the shell may assume the place which was
previouslyheld by SR. Actual superpositionthus attests equalityof
nee.
TIIK"II:F:M. "If a sphericalsurface be given,its centre is deter-mined."
For if an inner pointR be assumed ,-it a ^ivcn distance /)
from the surface, its focus is an interior continuous surface. Witliin
tins, at distance //. imagine a point I' to ^vnerafe a second c.,n

13. POLES AND PARALLEL CIRCLES. 5
tinuous surface,and it will be interior to the precedingand so con-tinually.
The series of surfaces must then necessarilyconverge
towards a singlepoint,which will be the centre of the given surface,
because the sum of the distances is the same, from whichever point
we calculate. The same argument proves that all the surfaces are
concentric spheres.
Poles of a Sphere.
THEOREM. "
To every pointon a sphereone oppositepoint lies
at the longestdistance along the surface." For if the pointP be
given,and we take a point$ at any distance from P alongthe surface,
and suppose S to vary under the sole condition that its distance
from P (alongthe surface)shall not change,the locus of $ is a self-
rejoiningline enclosingP. (We call this a circle.)Next, beyond
S, along the surface,take a new point T, which moves without
changing its distance from S and from P. This generates an outer
circle,cuttingoff a part of the surface which was beyond the circle
of S. Beyond this we may similarlyform a third circle,and this
series of circles ever lesseningthe finitearea beyond it,will neces-sarily
converge towards a pointQ on the sphere. P will then be
farther from Q (alongthe sphere)than any of these parallelcircles.
We call P and Q oppositepolesof the sphere. The distance between
them is evidentlythe halfgirthof the sphere.
Every pointon the sphere has not only its own oppositepole;
but also its system of equidistant(or parallel)circles. The middle
one of these (that is,the one equidistantfrom the two poles),is
called their equator.
If in an equator whose polesare P and Q, you fix any point
0, and then proceedinghalf round the equator fix a second point
D, C and D are evidentlyoppositepoles.
If you imagine a sphereto glideon its own ground,with centre
unmoved, you may suppose P to pass over to the site held pre-viously
by Q. This carries Q to the placepreviouslyheld by P.
Thus the poles are exchangeable,while the sphereas a whole is
unchanged and the same equator is attained.
THEOREM. "
If P and R be any two pointson a spherethat are
not oppositepoles,one equator,and one only,passes through them
both."

14. 6 THE STRAIGHT LINE.
Proof. Through P and its oppositepoleQ (justas above through
the polesC and D) an equator may pass. If this half equator PQ
become rigidand be rigidlyattached to the fixed centre A, it still
may sweep over the sphericalsurface (without change of P or Q)
until it passes throughR ; but after passingonce throughE, it does
not corne back to it,except in a second revolution. Q. E. D.
III. POINTS LYING EVENLY.
In Simson's Euclid, the line whose pointslie evenlyis called
STRAIGHT ; but the phrase"
lyingevenly"
is not explained.We can
now explainit.
When the two polesP and Q, and the centre A, all remain
unchanged,nevertheless each of the parallelcircles associated with
r and Q can glideon their own ground. Evidentlythen, if P and
A be fixed,this suffices to fix Q. In fact while each circle spins
round its own line,Q can onlyspinround itself.Also, to fix P arid Q
fixes A. "
These parallelcircles excellentlydefine to us the idea of
rotation,which is a constrained motion, still possible,even when P,
A, Q are all fixed. Now suppose that a line PMQ internal to the
sphererigidlyconnects P with Q. Then if the system revolve round
P, A, Q,PMQ may generate a self-rejoiningsurface within the sphere.
Again within this new surface a rigidline PNQ may connect P with
Q, and the line PNQ by rotation round P, A, Q may generate a
third surface interior to the preceding; and so on continually.Since
tliere is no limit to the constant thinningof the innermost solid,we
see that a mere line without thickness connects P with Q and passes
throughA, which line is interior to all the solids and duringrotation
remains immovable. It is called an axis,and can onlyturn about
itself. Hence every pointin this axis liesevenlybetween P and Q.
And since P and Q may representany two pointsin space, we
now discover that between any two there is a uniqueline lyingevenly.
This continuous line,while we talk of rotation round it,is entitled an
axis; but ordinarilywe call it simplySTRAIGHT.
On the StraightLine and its "
Direction."
We now infer that
1. Any two pointsin space can be joinedby a straightline.
2. Every part of a straightline is straight.

15. THE PLANE. 7
3. A uniquestraightline is determined,when its two end-points
are given.
4. Any part of a straightline,if removed, may take the placeof
any equal part of the same. Hence it easilyfollows that a straight
line,glidingalong itself,will prolongitselfindefinitelyfar,either way,
along a determinate course.
We are now able to sharpen our idea of direction. Hitherto we
might say vaguely,"
Imagine a path to proceedin any direction" that
is,without particularguidance. But now we see, that if ever so short
a straightline be drawn, it pointsto a definite prolongationbeyond
itself,of indefinite extent. This we entitle its direction. If this
direction be changed,a deviation there occurs, and a sharp corner is
recognizedat the point of deviation. The amount of deviation
suggests a new kind of magnitude, which will presentlyneed
attention. Now it suffices to remark on the case in which a new line
AZ deviates equallyfrom a previousline PA and from AQ the pro-longation
of PA. The equalityis tested by imaginingAZ to become
an axis of a sphere. Then if P and Q revolve in the same circle,ZA
is equallyinclined to AP and to AQ. It is called perpendicularto
PAQ. EvidentlyZ (on the sphere)is at the distance of a quarter
girthfrom every pointof the equator traced by P and Q.
IV. THE PLANE.
We return to the sphere. When any two polesP, Q are joined
by a straightline,it has been seen that this passes through the
centre A. The line PAQ is called a diameter of the sphere,and
its half (AP or AQ) is called a radius.
Evidently all the radii of the same sphereare equal;and of
different spheresthe greater the radius,the greaterthe sphere.
If an equator CDEG is midway between the polesP, Q, and D
is the pole oppositeto C, then as the diameter PQ, so too the dia-meter
CD, passes throughcentre A. This is true, whatever pointin
the equator is assumed for C. Therefore CAD is a varyingdiameter,
whose extremities trace out the equator,while the diameter traces
out a surface in which the equator lies. This surface is called a
PLANE, and in particularis the planeof the equatorialcircle.
It was seen that P and Q might exchange places,while the
centre A, and the sphere'ssurface as a whole, remain unchanged.
Necessarilyalso the planeof the equator remains unchanged. It is

16. Till: PLANK HULED HY A STRAIGHT LINE.
then symmetricalon its oppositesides,or in popularlanguage,the
plane turns the ^mne face towards P as towards Q.
The axis PAQ is called perpendicularto the planeof the equator,
g perpendicularto-every radius of the equatorialcircle.
THEOREM. "
No other line but AP can be perpendicularto the
planeof the equator,}*
Proof. For if AR be some other radius of the sphere,some one
of the parallelcircles,whose poleis P, passes throughR, and every
pointof this circle is nearer to the equatorialcircle than is the poleP.
Theivt""iv the distance of R from the equator is less than a quarter
of the sphere'sgirth,a fact which shews RA not to be perpen-dicular.
THEOREM. "
Through any two radii AP, AR of a sphere,that are
not in the same straightline,one planeand one only may pass."
It has Urn seen that through P and R only one equator can
pass. The plane of this equator is the plane that passes through
the two radii.
Cardinal Property of the Plane.
THEOREM. "
If M and N are any two pointsin a plane,no point
in the straightline which joinsM and N can lie offthe plane on
cither side."
Symmetry suffices to establish this truth. Our hypothesissupplies
data to fix what line is meant by MN, but givesno reason why any
pointof it should lie off the plane on one side rather than on the
other; for the whole line is determined by merely the extreme
pointsM, Ny of which neither can guideany pointtowards P rather
than towards Q. Thus there is no adequatereason for deviation
towards either side.
Symmetry of data is in other mathematical topicsacceptedas
an adequateargument for symmetry of results. Otherwise,"the
want of sufficientreason for diversity"passes as refutation of alleged
, sity.Therefore the argument here presentedhas nothingreally
novel.
We have now a new method of generatinga plane that shall
pass through two intersectingstraightlines LM, MN. Along ML
let a pointE run, and along MN similarlya pointF. Join EF
while the motion of E and of F continues. Then EF (bythe last

17. THE PLANE EVERYWHERE LIKE ITSELF. 9
Theorem) alwayscontinues to rest on the plane LMN. This mode of
generatingthe planesupersedesthe idea of rotation. For simplicity
we might suppose ME : MF to retain a fixed ratio.
THEOREM. "
A planehas no unique pointor centre."
For if we start from given sphericalradii AP, AR through
which passes an (equatorial)plane,in AP take M arbitrarily,and
in AR take N arbitrarily.Then we have seen that the locus of the
moving line MN is our given plane. But again,in this plane take
a fixed point 0, and join 0 to fixedpointsM and N. Then from the
lines OM, ON we can (as in the last)generate the very same plane,
which can glideon its own ground as the spheredid ; thus the point
A can pass to 0 without changing the ground or surface as a whole.
The plane is infinite,the sphereis finite; but as with the sphere,
so with the plane,no pointof the surface is unique.
After this,no impediment from logicforbids our passingto the
received routine of Plane Geometry, until we are arrested by the
difficultyof parallelstraightlines,to which I proceed,after one
remark on the definition ofan angle.
Above, a sharp corner or turn was identified with deviation,or
change of direction. In geometry it has the name of an angle,and
we measure its magnitude by aid of the circular arc which it sub-tends
at the centre or by the sector of that arc. But no insuperable
logicforbids our estimatingthe magnitudeof an angleby the portion
of the infinitearea which it interceptsfrom a plane; which indeed
is suggestedby a perpetualelongationof the radius of the circle
whose sector was assumed as measure of the angle.
Monsieur Vincent in Paris (1837) adopted this definition as
adequate to demonstrate the equivalentof Euclid's Twelfth Axiom
without any new axiom at all. Has this method received due
attention in England ?
Monsieur Vincent was not the first to suggest acceptingthe
infiniteplane area cut off by two intersectingstraightlines,as the
measure of the anglewhich they enclose : but perhapshe was the
first to introduce the method into a treatise on Elementary Geometry,
that obtained acceptance in so high an institution as the University
of France.
Two lemmas alone are wanted, and these every beginnerwill find
natural.

18. 10 PROOF OF Tin; TWELFTH AXIOM.
LEMMA I. "Every angle is a finite fraction of a rightangle;"
that is,some finite multipleof it exceeds 90". For the circular arc
which subtends it,is always some finite fraction of the quarter of
the circumference.
DEF. When two straightlines AM, BN in the same plane are
both perpendicularto a third straightline AB, we call that portionof
the planearea which is enclosed between MA, AB and BN a BAND.
LEMMA II. Then, I say, whatever the breadth (AB) of the band,
UK area of the band is less than any finite fraction of a rightangle.
Proof. Prolong AB indefinitelyto X, and along it take any
number of equal lengthsAB = BC = CD = DE, "c., and through
G, D, E... draw perpendicularto ABODE... straightlines CO, DP,
.c. Evidentlythen the successive bands are equal,by superposi-tion.
Thus, whatever multipleof the first band be deducted from
the plane area marked off by the right angle MAX, the loss is
iiiM nsible ; for,as remainder,we find the area marked off stillby a
rightangle(such as QEX, if onlyfour bands were deducted). Any
two rightanglesembrace areas which can be identified by super-position,
and have no appreciabledifference. The matter may be
conciselysummed up by remarking,that every band is infinite in
one direction only,"
say, horizontally" but the area embraced by any
rightangleis infinite in both directions,horizontallyand also verti-cally.
Thus it is no paradox to say, that no finite multipleof the
band can, by its deduction from the area of the rightangle,lessen
that infinite area in our estimate. Q.E.D.
Euclid's Twelfth Axiom is now an immediate corollary; viz. If
MABN be any band ; and, within the right 3
N
angleNBA, any straightline BT be drawn,
11 be prolongedso far as to meet the
prolongationof AM. For the angleNBT
'r.'H-tionof a rightJin-lf,while
T
i li"-ban"l J//;.LY is less than any Unite fraction of the same; hence
the angle NBT is greater than the band MABN, but unK-ss /""/'
AM this would be ials".
Thus of necessitythe two lines
do cross, as we assertril.
I cannot see
any new axiom involved in this proof:therefore
I am forced to abandon several other speciousmethods and give it

19. VOLUME OF PARALLELEPIPEDON. 11
preference. Surely we may bow to the authorityof the University
of France in such a matter.
On the Volume of Pyramids and Cones.
The treatment of this topicin Euclid is very clumsy. It demands
and it admits much improvement.
1. For parallelepipedaprove first,that if two such solids differ
solelyin the length of one edge,which we may call x in the one
and a in the other, then their volumes are in the proportion of
x : a.
2. Next, if they have a solid angle in common, but the edges
round it are in one xy y, zt and in the other a, b,c, then the two
volumes are in the proportionof xyz : abc.
3. After this it is easilyshewn that parallelepipedaon the same
base and equalheighthave equalvolumes.
4. Therefore finally,that the volume of a parallelepipedonis
measured by its base x its height. Con. The same is true of any
prism.
From this we proceedto approximateto the volume of a pyramid.
5. Divide the height(h)into (n)equal parts by (n" 1) planes
all parallelto the base (B). Establish, on these (n-
1) bases,
upright walls, and you will find you have constituted a double
system of prisms,one interior to the pyramid,one exterior; the
latter has the lowest prism in excess of the other system. Every
base is similar to every other, by the nature of a pyramid. The
volume here of every prismis - x its base,the number n and -
being
the same for all,but the base varying.
6. The base whose distance from the vertex is -.h, is to the
r2
original(B) as r2 : n2; hence its area is
jji"ftwhich givesfor the
volume of the prism standing on it (^.
BJ.
-
.
Hence the sum of
l2 + 22 + 32+...+ rca h "
f
the volumes of the external prisms is -
^
-
.
-
.
#, a
by omitting ?i2from the numerator of the largerfraction we obtain

20. '2 YoU'Mi: OF PYRAMID.
thi- Mm i
""t' volumes for the internal prisms. Now since -
.,'
when It, /" arc finite and n infinite, the difference of the
systems
ot' prisms vanishes when n
is infinite. But the volume
of the pyramid is less than the exterior system and greater than the
interior: hence each system has the volume of the pyramid for its
limit, when n
increases indefinitely.
7. Let
fj,
be the unknown numerical limit to which the fraction
1s + 22 + 32 + ?i2
"
,
"
approximates when n
thus increases. Then the
volume of the pyramid =
/j, .
h
.
B. Since
//,
is the limit of a
numerical
tract i""n, which remains the same,
whatever the form of the pyramid's
base, we
shall know the value of
/z,
for all pyramids, if we can
find
it in one.
Meanwhile the result V = /j,.h.B at once shews that
pyramids with equal base and equal height have equal volume, since
IJL
is tin- same for all.
8. When this theorem has been attained, we have only to divide
a triangular prism into three pyramids, and instantly infer that the
3 are equal among themselves; therefore that each has a
volume
just " of the prism, i.e. equal $h.B.
This, being proved of a pyramid whose base is a triangle, shews
that the unknown
//,
is there exactly J.
Hence universally ji = J, and volume of
every pyramid = J/t .
B, or
is equal to J of the prism which has the same base and height.
COR. Every cone also is one third of the cylinder which has the
same
base and height.

21. TEACT II.
GEOMETRICAL TREATMENT OF V~l-
1. In
pure algebra, concerned with number only, the symbols +
and "
,
denoting addition and subtraction, in an early stage needed
elucidation when the mark of minus was doubled. It is found natural
that "
(+ a) and + (" a) should both mean "
a, but that "("a) should
mean + a,
and (- a) .
(- 6) should be + (db) surprises a beginner, and
is illustrated by urging that to subtract a debt increases the debtor's
property, and to subtract cold is to add heat. But as soon as we
apply algebra to geometry, the symbols + and " are still better
interpreted of reverse direction; also time past and time coming
afford equally good illustration. Distinguishing positiveand negative
direction along a line, we find no mystery in the fact that to reverse
negative direction is to make it positive,so that " (" a) gives + a,
as reasonably as " (+ a) gives "
a. If we know beforehand whether
a given distance is to be counted positively or negatively along a
given axis, no ambiguity is incurred, and the sign + or " generally
gives the needful information. For this reason some are apt to think
of + a and "
a as different numbers, instead of the same number
differentlydirected. Out of this rises the learner's natural complaint
when he meets V" 1 or V~ 5. "There is no such number: you confess
it is imaginary: a proposition involving it has no sense." So murmurs
every scrupulous and wary beginner: and the teacher's reply, "Some-how
we work out useful results by /- 1," sounds like saying: "Out
of this nonsense useful truth is elicited."
2. The first reply to be made is: No one ought to desire any
number for iJ" except the unit itself; the V~ which precedes,
though a double symbol, has the force of a symbol only. The next
reply is decisive, "
the double symbol V- points to a new direction
in geometry; namely, the direction perpendicular to + 1 and "
But to explain this fully,it is better to make a new beginning.

22. 14 WARREN'S RADII.
Suppose that radii issue in many directions from a fixed pointin
a plane,and that distances are counted along them. So long as we
know along which radius we are to count, nothingnew is involved,
and of course no difficulty.Suppose one of these radii to be our
ordinary positiveaxis,another to be called the m radius, and for
distinction write the index m under every number to be counted
along it,so that lm is its unit,in length= 1 as estimated absolutely.
Then we deal with ambmcm...along the m line,and combine am " bm,
and interpret5aw, obm " 6cm, without difficultyor fear,since all are
lengthsto be counted along the same radius. But such a product
as am . bn would need careful interpretation.In abn no obscurityis
found, whether the a be linear or numerical. If linear,we proceed
as in interpretingab3,though space has only three dimensions. If
we put A for the value of ab3,we attain it by the proportion
= b* : A, so that A is the same in kind as b3. Similarlyif
A'=ab", we are able to count A' alongthe n radius,whether a be
simplynumerical, or when it is linear,by aid of the ratios 1 : a = bn: A'.
But if we proceedthus with am. bn,usingthe proportion
we confound ambnwith abnfor 1OT: am is the same ratio as 1 : a.
3. Mr Warren in 1826 laid a logicalbasis for this matter by his
ise on ^"l, which I here substantiallyfollow,and wonder that
it is not found in all elementary works. He virtuallydistinguishes
between proportionatelengthsand proportionatelines. In the former,
DIRECTION is not regarded;with the latter,it is essential. Thus if
4 1,
/",C, D are proportionatelengths,but are drawn alongour radii,
"
viz. A alongthe positiveaxis,B along the m radius,C on the n
radius and D on the p radius,we do not pronounce these lines pro-portional,
unless also their directions justifyit;that is,the p radius
b"- disposedtowards the n radius,as is the m radius to the
axis. This amounts to sayingthat the p line must He on
tin- -aine side of the n line,and at the same
angulardistance from it,as the m line com-pared
with the positiveaxis. Then, if OL,
""M, ON, OP I*- tin 4 radii,and LMNP a cir-cular
arc, we need that the arc PN shall
= arc ML before we admit that the units
v k.
OL, OM, ON, OP are proportionatelines.
Alt"T this condition of the directions is fulfilled,we concede that

23. WHEN PROPORTIONAL. 15
the proportionatelengthscounted alongthem are also proportionate
lines.
If the arc NP = arc LM, add MN to both, then arc PM = arc NL.
This enables us to exchange the second and third terms in the pro-portion,
agreeablyto the process called Alternando. Also the arc
PL = PN+NL=ML+NL. Hence if we count from L, and call
arc LM" m, arc LN =
n, arc LP =
p, the test of necessary direction
is p = m + n.
The simplestcase is,when the four proportionalsbecome three
by the second and third coalescing,as if M and N run togetherin Q.
Then if arc ZQ = arc QP, we have OL : OQ= OQ : OP. If further
arc PR = arc PQ, then OQ : OP = OP : OR] and so on.
4. Apply now this to the case in which the arcs PQ and QL are
both quadrants.Then OQ is the mean pro-portional
between OL(= 1) and OP=(" 1).
The received symbol for a mean proportion
is V, as in OQ = *JOP .
OL. Here then
OQ =
V(- 1 .
1)= V- I- This is only a fol-lowing
out of analogy with the symbol;
though, previously,V expressedthe mean
proportionbetween numbers, or perhapslengths,without cognizance
of direction.
Now, our first care must be, to inquirewhether V~ as a symbol
of direction,has the same propertiesas when it operates on a pure
number.
First,in combining factors,the order is indifferent,as ab = ba,and
a .
(1)= a = 1 .
a. We ask, does V~ fulfilthis condition? Evidently,
a. ^-1 =
^-1. a, each measuring the lengtha, directed alongthe
perpendicularOQ. Similarly
Next, repeat */-" We had OQ = OL*/-I or "/-!. OL. Also
OP=J-I.OQ, because QOP = 90", .'. OP = V~ 1 .(V -
1 "
OL).
But OP = - OL or -
1 .
OL. Evidentlythen V -
1 .
V - 1 is equi-valent
to - 1. This further justifiesthe change of
-j"^
to -*J-.
5. But a new difficultyarises in adding unlike quantities,i.e.in
connectingthem by +. If along radii m and n we have two lengths
a and b ,
what meaning can we attach to am + bj. This urgently
needs explanation.It may seem that the symbol+ (plus)receive

24. 1C SIGN + NOW FOR TOTAL RESULT.
a now sense. " Now in fact when (a+ 6)=
zero, the + does not strictly
mean addition; it reallyexpresses a difference,not a sum; but not
to embarrass generalization,we call it a sum, and say that either a or
b is negative.They may mean the very same line OL estimated in
oppositedirections,as OL and LO. If OL mean the line as travelled
from 0 to L, and LO the same as travelled from Z to 0, the state-ment
OZ + LO =
zero, clearlymeans that the total result of such
travel is nothing;since the travel neutralizes itself.Thus if,instead
of sayingthat the sum is zero, which givesonlya numerical idea,I
call total 7"esultzero, you will gain a geometricalidea. At this we
must aim, when we deal with lines differingin direction. Evidently,
if,startingfrom any pointin the outline of a limited surface,a point
travel round the circuit,until it regainits originalplace,we may
justlysay, the total result of such change is zero; and no one will
suppose it to mean that the lengthof the circuit is zero. So if there
be a triangleABC, we may say, the total result of the travel
AB + BC + CA = 0, if it be understood that each line is to be esti-mated
in a different direction. Indeed, suppose the lengthsof the
three sides are c, a, b, then in the equation cm 4- an + bp= 0, the
symbol -f cannot mislead us, though its sense is evidentlyenlarged
from sum to total result.
Again,since AB + BC+CA = 0 and G A = -
AC, when direction
is considered,we have AB + BC " AC =
0, which further justifies
AB + BG = AC. The last is interpretable,"
"
Motion along two
successive sides of a triangleyieldsthe same total result as motion
along the third side."
The word resultant characterizes mechanics, but there seems no
ol.j(ctinn to adoptingit in geometry also for the total result,as
distinguishedfrom the sum.
In fact we have unawares made a great step forward; for the
symbol *J" now en;il"lcs us to express distance in every direction. If
our parallelogrambecome a rectangle,and AB isthe ordinarypositive
before),the lengtfisof AB, BC, CA are c, a, b,we have
BC=a"J " 1 when direction is estimated,and A C = total result of c
and a V" 1, or AC (an obliqueline)= c + a /" 1. Since c and a are
independentlengths,AC may have any direction whatever.
lint again,we must inquirewhether the symbol+ ,
thus extended,
can be worked in the received method. First,does it fulfil the
fundamental condition expressedl"yA + B = B + A ?
Assuming (as

25. CONFORMITY OF V~ TO ALGEBRAIC LAW. 17
we must) the doctrine of parallelstraightlines,and consideringany
rectanglewhose sides are a and c, we find
that c+a"J" 1 = th e diagonal= a /"
1 + c
from the oppositesides. Next, does it-
fulfilthe condition h(a + B) = hA + hBI
The doctrine of similar trianglesat once
affirms it. Let OM =
x, MP =
y, per-pendicular
to it; joinOP, then if 0 M is
the positiveaxis,and y expresses mere
length,we write
OP or OM + MP =
x + y"J-.
Next, along OH take Om = hx',that is 1 : h = x : Om (whether h is
linear or numerical).Erect mp perpendicularto Om and meetingOP
in p. Then by similar triangles,mp = h . y (inlength)and Op=-h. OP.
In this h .
OP "
Op we have supposedh to be numerical.
Also OP is equivalentto x + "J" 1 .y,
and Op to Om + fnp"J" 1 or hx 4- f"
1 . hy,
that is, h(x--"J"ly)"
hx + V - 1 " hy,
justas if V" 1 were numerical.
If further we change h from a mere number to a positivelength,
it affects every term of the last in the same ratio,and leaves equi-valence
as before.
If we have proved generallythat with any factor h (provided
it be counted alongthe positiveaxis)the producth (x+ V" 1 " y) is
equivalentto hx + ij"l. hy, the same is virtuallyproved,if h be
changed into hm, that is,if the numerical h be computed alongan
m-axis. For we may transform our hypothesis,by choosingthe m-axis
as positive.If herebyx, y change to x'ty',we obtain a result the
same inform as the previousresult,and x',
y'remain quiteas general
as were the x, y. Thus we may write
^ "
0 + V- ly)= hmx + J-l. hiny.
After this,we can change the obliquehm into a + */-l.b, where a. b
are alongthe positiveaxis. Now if the m-axis be perpendicularto
the positive,we may write simply hm = kj- 1, where k is alongthe
positiveaxis. Then V - 1 "
hmy =
/-
1 .
V -
1 . kytand since each V - 1
N.
2

26. 18 CONFORMITY OF ^ - TO ALGEBRAIC LAW.
denotes revolution of the ky through 90", the "J" 1
.
^-1 shews
revolution through 180", or is equivalent to the symbol "
.
Thus
= /y7" 1 kx " ky
"lyas?yV" 1 were numerical. Evidently then the same holds
good in multiplying out (h + "J" Ik) into (x + /" I?/).
THEOREM. If ^1 + " V- 1 =
"? + ^ V- 1, this implies Zwo equali-ties,
viz. A =
(7 and B =
D. The geometrical proof appeals at once to
the
eye.
If OA be the positive axis, and
the binomials are denoted by OP and OQ,
viz. A + V-15 =
OP and (7 + V- ID = OQ,
we do not account OP = OQ until they
have the same direction, as well as the
same length. This requires Q to coincide
with P. Of course then, if PM, QN are
dropt perpendicular to OA we have Oif =
v
B"/"1, ON= C,
QN=D /" 1, and as soon as OP= OQ in our hypothesis, P coincides
with Q, therefore also M with jJV. That is A =
(7 and B = D.
The reader will now see the geometrical meaning of the "imaginary
roots" (so called) of a quadratic equation. As a very simple case,
take first
a? -
IGx + 63 = 0, which yields x =
8 " 1.
Here both roots lie along the positive axis. But change G3 to 65,
then a? "
I6x -1-65 = 0, whence x =
8 " V" 1.
In the latter the two roots are equal radii drawn from the origin
at equal angles on opposite sides, radii which terminate where the
coordinate along the axis is 8, and the transverse coordinate is " 1.

27. TRACT III.
ON FACTORIALS.
SUPPLEMENT II.
Extension of the Binomial Theorem.
1. THE following appeared in Cauchy's elementary treatise, as
early, I think, as 1825, but without the new Factorial Notation, which
adds much to its simplicity. Boole writes #(2) for x (x - 1), #(3) for
a? (a;-1) (2?-2), and xw for x(x- 1) (a?-2) ...
(x- n+ 1), whence
a)(n+l]=
x(n)
.
(x "
n). Better still it is, to place the exponent in a
half-oval, since a parenthesis ought to be ad libitum. I
propose
which are quite distinctive. Then the Binomial Theorem is
In this notation 1
.
2
.
3
.
4
...
n or n (n - 1) ...
2
.
1 is n^. Guder-
mann for this has n ;
but (n " 1)' is less striking to the eye
than
n, In "
1 introduced by the late Professor Jarre tt. This exhibits in
the Binomial Theorem its general term, by
1 + xn = + n
.
+ ...
+ n
.
+ .
of course x^L" is equivalent to simple x.
The Exponent (of a power) is already distinguished from an
Index. In a Factorial x^ for x (x -
1 ) (x - 2) . . .
(x - r - 1) one may
call r (which must be integer) the Numero, as stating the number of
factors.
2"2

28. 20 EXPANSION OF (x -f J))^.
2. If 771,n, p be all positiveintegers,and p = m -f n, then
or, in condensed expansion,
This equationbeing of the (m + n)thor pilidegree of x, and being
true for values of x indefinite in number (thereforein more than
p values),must be equal term by term for every power of x. Now
when we multiplyany two such series,
(1+ Mvx + Mj? + M3x*+ etc.)by (1+ Np + Nj? + etc.),
we have a productof the same form
by the routine of multiplication,in which
P^M^NJ P^MI+M^ + NJ P^M^
and the law of the indices is so visible,that we get generally
This being true for all series of this form may be appliedto the
three series (1+ x)m,(1+ a?)",(1+x)p, and at once it yieldsto us the
result
n mC n mC n
+ '"" + ''""" "
an equationtrue for more values of m and n than are counted by the
integerr, therefore it is true also when m and n are arbitraryand
fractional. Write x for m, h for n, and x + h for p, and you have an
extension of the ordinary(x+ h)r. For, this latter may be written
of of'1 h x*-* ^ aT3 ^ "
rr-j 'I* r-"2' 2+ r-;r':l4 r'
with exponents replacingthe numeros of the preceding.
NOTE. The reader must carefullyobserve in that which follows, that the upper
itub's of /', Q, A, /.',('. is not an exponent.

29. POWERS IN SERIES OF FACTORIALS. 21
Powers in Series of Factorials.
3. Since x^L" =
x(x"l)=xz "
x,
of which the generallaw is
x^ (x-r) = a*iJ,
conversely #2 = x^L + x.
Again oxL = x (x-
1)(x-
2)= x3 -
But
Evidentlywe can thus in succession obtain x4,xs,...and generally
xn in series of x^, x1^, x^,... x"^, x.
Since onlyx^ contains xn,its coefficient must be 1. In general,
with unknown coefficients P, dependent on n, but not involvingx,
we may write
xn =
P"Q.
x^ + Pr1 tfO1 + Pr VxJ + ...
+ P^_2^i, + Pi^a?..
.(a).
Here the lower index denotes the placeof the term in the series ;
the sum of upper and lower index =
n, the exponent of xn ; and the
upper index is the same as the numero of its term. We have also
seen that P"= 1, whatever n may be. It remains to calculate P"~r.
Multiplythe left member of (a)by x, and on the rightmultiplythe
successive terms by the equivalentsof x, viz.
(x-ri)+ n, (x-
n + 1)+ (n-
1),(x-
n + 2)+ (n -
2),etc.,
and applyto each term the formula x^ .(x"
r)= xr^2. Then
But if in (a)we write (n-f 1) for n, we have
and we cannot be wrong in identifying(6)and (c); that is,in equat-ing
the coefficients belongingto every particularnumero (r). At the
right hand end PJ,= lPln-l}coefficients of x i.e. since when n = 2,
ic2= oxL + x, so that P = 1,
.
pi _
i Pl "
I "
. "
-t
2
" -1
" ^a"-1?

30. INVESTIGATION OF TABLE
and universallyP,l,=1,justas Pj = 1. Also in generalwe find
P"- _
^pr i pr-1
"*"
n+l-r
~~
' "*"
n-r " *
ti+l-r"
otherwise, P^rP^ + PJ'1,
if p = n + 1 "
r.
This enables us to fillin the vacancies of a table,beginningfrom
one horizontal row and one vertical,each consistingof units. Each
P is computed from the P above it,multipliedby its upper index
(which is the number of its column) + its companion to the leftin
the same row. Thus to form the second row from
Evidentlythis second row is
1; 1 + 2; 1+2 + 3; 1 + 2 + 3 + 4;...
of which the generalterm is P^=n. (n + 1). Similarlyfrom the
second row we form the third,workingfrom leftto right,and the law
is manifest.
Heuce a table to any extent requiredcan be made, such as is here
presci

31. TO CONVERT POWERS INTO FACTORIALS BY P. 23
When this table is used solelyto evaluate the coefficientsof (a),
the indices of P^Pp1, P"~2...warn us that the numbers will be taken
out diagonally.Thus for a? we take out (beginningfrom PJ at the
top on righthand) 1, 15, 65, 90, 31, 1.
It will be observed that the second column is 21 "
1, 22 "
1, 23 " 1
and in generalP* = 2r+1- 1.
Such is the Table of Direct Factorials.
The letter P being almost appropriatedfor the Legendrian
functions,I see an advantage in supersedingP"rby I/^ .
Neces-sarily
n and r are both integers,n index of the column, r + 1 index of
the row.
Collect the results for P
and in general
which yieldidentically
P=
#C2 + etc.
Factorials in Series of Powers.
4. This is a mere problem of common multiplication,
0^ = "(*-!) (a?-2)...(ff-.n+ l),
yet the factors beingspecialand their combinations often recurring,

32. 24 INVESTIGATION OF TABLE
the work of one computer may avail for many after him. We may
assume
x^ = Qn0xn-
Qrlxn~l+ QrV-" - etc. ...
" Ql,x ......
(");
where, as before, obviouslyQj=l. Also dividingby x, and then
making x = 0, you have
Since (x "
n) x^ = xn^y
multiply(a)by x "
n,
Also in (a) write n + 1 for n ;
But (6)and (c)ought to be identical. We have anticipatedthe
remarks that Q"+1= Qo =
1, and Qln=nQ_ltinasmuch as
But generally, Q'^ = nQnr~r
+ Qnr^',
or, if n -
r =
m, Q?+l=
(m + r)"" + $".
As before,this enables us to continue the table,when the firstrow
and firstcolumn are known. To compare our formula with that of
the firsttable,we may write it
In fact,the firstrow is unityas before. The firstcolumn is
1, 1, 1.2, 1.2.3, 1.2.3.4,
when r =
0, Q? = mQ? + Qf1,
also in the former table,when
n =
r, lJr1=rPf0+ Prl-1.
Hence the second row is the same in the new table as in the old.
To compute the third row from the second :
1
1.2 11
6
= 35
10
= 85
15
= 175
21

33. TO TURN BACK FACTORIALS INTO POWERS BY Q. 25
The multiplierr + (p"l) combining upper and lower index of
its Q distinguishesthe Q table from the P table: thus
1.2.3
1.2.3.4
or indeed
Inverse Factorials.
These too are used diagonallyfor Thus
Again it seems better to supersede
by
5n"2+ etc.
5. Even in Arithmetic we are driven upon
"
recurringdecimals,"
and learn that an infinite series may tend to a unique finite limit.
Nor can Elementary Algebrafailto recognize,from
l-xn
l-x

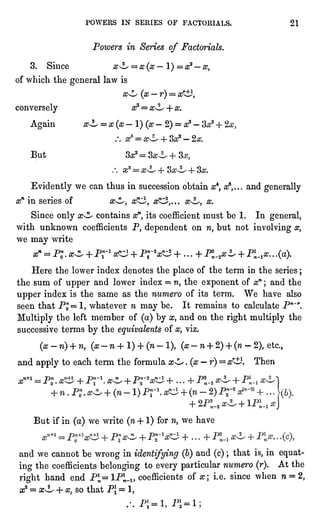
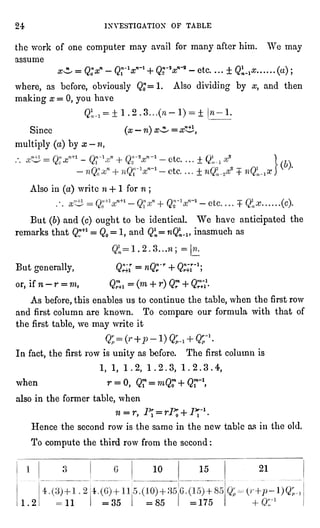
34. 26 WITH A NEGATIVE NUMERO
that when x is numericallyless than 1,with n indefinitelyincreasing,
the series 1 + x + a? + . . .
-f xn tends to the limit
n
l "
x
After this it quicklyfollows (by Cauchy'sprocess now perhaps
universal),from Binomial Theorem with n positiveinteger,that
(1"1 + -J with n infinite,has for limit
17
+^=2-7182818...
which we call e, and that f1 + -J has for limit
which also = ea. On this we need not here dwell : but it will
presentlybe assumed. Now let us propound
Factorials with NegativeNumero.
6. Analogy suggeststo define x^ as meaning"; --
-^
: of course
x x ~H 1}
x^ will be identical with x~l. Then x^ will stand for
and x^" for [x(x+ 1)(x+ 2) . . .
(x + n -
I)]"1.
Hence x^J = (x + n)~l.
#O.
Now x^ = (x H-l);*;^,
and when x is " 1,we have, in descendingpowers
x^ = x~* " x~3 + x~4 - x~b 4- etc.
Also x^ = (x+3y.x^"
of the two factors here on the right,each can take the form of
a series descendingin powers of x. So then their product,the
"liivalentof x^l". By like reasoningwe claim a rightto assume
with coefficients independentof x,
x^ = A;x-n-l-A"1x-n-z+An,x-n-3-etc.......... (a),
and our task is to discover the coefficients when n is given.

35. THE TABLE OF P SUFFICES. 27
First make n =
1,
But from the series alreadyobtained for x^ we see that every
coefficient of the last is 1 ; or in generalAlr=I. This givesthe first
column of our table. Also universallyAn,obviously= 1 ; which fixes
the firstrow of the table.
Next, multiplyequation(a)by (x + n),and you get
s~M 2" etc. ...
+ A"x~n~r+ ..
But in (a)we may write n for n + 1, which gives
x^ =
x-n-A^lx~n~l+... "A?~1x~n~r+ ............ (c).
Now (6)and (c)must be identical,hence
Al=n + Arl=nAl+Ar
and generally A^nA"^ + Anr~l.
But this is exactlythe law of P in Art. 3, only there we had r, p for
what are here n, r. Now as the first row and first column are here,
as there,unity,and the law of continuation the same, the whole table
will be the same, and we may write P of Art. 3 in place of this A.
Thus we get
x" = x~n -
Pr V"-1 + PJ-V""1 -
P3n-Vn'3 + etc. . . .
with the same values of P as before. But in the last equationwe no
longer take the P's diagonally,but vertically,down the column, as
the same upper index (n "
1) above every P denotes ; thus
T7 - etc. . . .
To verify,multiplyby x + 2. But for convergence x ought to
exceed 2. So
f
4
- 90af5 + etc. . . .
and for convergence, x oughtto exceed 3. Evidentlyin the series for
,
x ought to exceed (n"
1).
7. Assume now the Inverse Problem, to developx'n in series of
Factorials.
With unknown coefficients B independentof x, we start from
x-n-l = x^+Btx^J + ]%x^J+ ...............
(a).

36. 28 FOR THE INVERSE PROBLEM, Q SUFFICES.
Multiplythe lefthaud by x, and the successive terms on the right
by the equivalentsof x, viz.
(x + n)-n, (a-+ n + l)-(w + l)f(aj+ n + 2) -
(n + 2),etc.
Observe that (x+p) a,'-*""= x(~p)"
-...'
But in (a)we may write n for n + 1,which gives
^J+...+Bnr-l.x^r+ ...... (c).
Identify(6)with (c),
.-. J3T=n + "rl;
and generally Bnr=
(n + r -
1)B*^ + Bn/1;
the same formula as for Q in Art. 4, only n and r here standingfor
what there was r and p. Also since .Bj=l, the top row is unity,
here as there.
We may further prove that the first column of our J5's is the
same as the firstcolumn of the Q's. For
Multiply by x on the left,also by (x + 1) "
1, (x + 2) -
2,
(x+ 3)"
3, for the successive terms on the right; then
Obviouslyx~l = x^ ; and the other terms must annihilate them-selves,
making ^-1=0; B -
2B = 0 ; B -
SB] = 0 ; etc.,
or B = I, ^ =
2^ = 1.2;
JBJ=3B;=1.2.3, and Bln=l .
2 .
3 ... (n- l)n.
Thus B=Q, BI =
Q13)etc. exact. Therefore the B table is the
same as the Q table throughout.
Here also we take the Q's vertically,to obtain x~n in series of
factorials as x~4 = x^ + Ga;^ + 35^ + 225#^ -f etc.
In generalx~" = x^ + Q^x^ + Qrlx^~? + ...
+ Q;*1.^C^r + etc.;
but specialinquiryis needed concerningconvergence. Apparently
it converges more rapidlythan
x*+(js -hi)'2+ (a+2)-f+ etc.

37. NEW PROBLEM. 29
8. To develops (e'-l)" or {?+
*"
+ ^+
jj+etcj"in powers
of xn. We may assume for this the form
Mnxn + Mn+lxn+l+...+Mrx' + etc.,
where Mn manifestly = 1, and if r is less than n, Mr = 0. Now by
the Binomial Theorem where n is a positive integer
(e*- 1)- = e- -
? ""-"" + ^ .
""-"* _
etc. "
? e* +1,
out of which we have to pick up the partial coefficients of xr which
make up Mp observing that
1
1
'
2 13
in which we have to make p successivelyn, n- 1, n- 2, ...
When
we make p =
n, the only term that here concerns us is - -
.
When
A^ f/yr
--
"I )** fyF
p = n - 1, we get -
j .
- "
rf- -
.
When p = n - 2, we have
and so on. All have r in the denominator. Hence
of which the last is + -
.
I2.
Let N be to (n + 1) what if is to n ; then, with r the same for both,
terms.
l,....
If I-
Add this to the preceding, coupling every pair that with the
same value of p
has (n "
p)r as factor ;

38. 30 COMPARE J/r+ .Vr WITH N^.
n + 1 Ti + 1 ,
7i - 1 71 + 1
,
n - 2
Observe that " -- 1 =
n, -
-^
---- 1 =
9 ,
"
^
-- 1 =
^
"
and so on ;
.-. |r.
(Jl/r+ J"TJ= (n + 1)"-
j
(n)'+ *-"^"("-
1)'-
etc.,
or, in shorter notation,
= (TI+ I)'- ^.
(")r+ ^ .
(n-
l)r-
^ .
(n-
2)'+ etc. to (n+ 1)terms.
But in Nr change r to r + 1 and you have
r + 1 .
A;.,=
(n + IP -
^ (")"'+ **in
C"-
V"
- "^^o'-
Q"
l
"
("-
2)r"+ etc- " " "
to (n+ 1) terms
("+ 1) {(n+ 1)"- 1(ny +
n--"~--1
(n -
1)'
w. n-1 .
w " 2 ,
1.3.8
("-2
(T?-f-1). |r(Mr+ Nr),from above. Divide by (n+ 1). |r-f 1 ;
Our r always exceeds n. We simplifythe notation somewhat by
assumingas coefficients after dividingby xn,
z!V=i +
^H .
+ _
^ _
+
.
7i + 2 . . .
n -f p
Multiplyby xn. The generalterm becomes
4 etc.
(n+ 1) (71+ 2)...(n+p- 1) (71+ j")
'

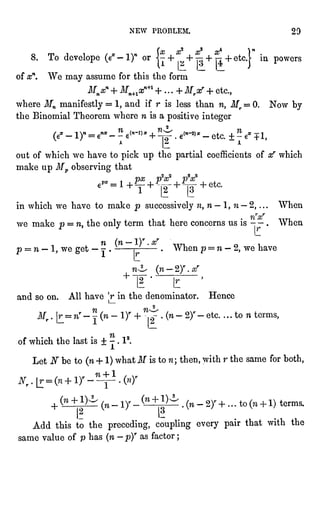
39. THE TABLE OF P AGAIN SUFFICES. 31
Put n + p -
r, to identifythis term with our previousMr .
xr ;
.'. M =
*5="
w + l.w-f 2-. 7i + 3 ... (r-1) .r'
Cn+l
so that
^rr=n+ 2tn-^3~1r__l r
with one lessfactor in denomina-tor:
but when both n and r in Mr are increased by 1,r -
n undergoes
no change; and N ^
= r~n
" + 2.n + 3... r" l.r.r-hl'
Introduce these values into (a)and multiplyby
Change r -
n to p and n + 1 to n, .'. Cnp=
Cnp~l+ nC;^ ; the same
law as for the P's in Art. 3.
Also when n =
lt
But we assumed as equivalent
01* OX cx_ ex
2 "^S.S^S.S.^"1" "t"2.3...(r+ l)
which identifies (7Jwith 1,for all values of r. Just so Plr= 1 in its
first column. Also evidently"7j=
l; justas PO=!" in tne whole
first row. Thus, with firstcolumn and firstrow identical with those
of P and the same law of continuation,the whole table is the same.
Finallythen we obtain
-iy pj.a?
= i+
in which the increasingnumerators are pulleddown by increasing
denominators.
The generalterm may be written n^ . Pnp.
xp, or equally
(n
[The course of analysishere pursuedforestalls that of A" .
Or to
the learner.]
Thus
"?
+ l n + 1 .
n + 2 n + 1 .
w + 2 .
n + 3

40. o2 PROBLEM OF LOG (1-f ?/).
9. To investigatelog(1-f x) in series,with no aid from (1+ x)n
except in the elementarycase of n being a positiveinteger,and no
aid from the Higher Calculus.
Let y = e* "
1, then x =
log(1+ y). Also
x of xs
by elementaryalgebra.
From the last we see that for minute values of x, as a first
approximation,y =
x, and a? =
y*. As a second, y = x + x*"= x + Jy2,
/. x=y- Jy2. Whatever the series in powers of x, x can be thus
reverted into powers of y, at least within certain limits. Hence we
may assume with unknown coefficients called A,
x or log(1+ y) =
y -
A^f+A3y*-A^4 + etc ....... (a),
which (withthe appropriatenumerical values of A^A3A4...)will be
an identical equation.
Consequently,writingy + z for y,
log(l+ y + z) =
(y+ z) -
Az(y + z)*+ A3 (y+ z)3+ etc. ...
(6).
Subtract (a)from (b)developingthe powers
then og(l+y + z)-og(l + y)=z-z
+ A, (tyz + Zyz*+ *3)-
A, (Itfz+ Qy*z*+ 4^2 + z4)+ etc. . . . (c).
But the left hand = log.
" -
or log(1 -f :="" jwhich again,
by (a),if we write - -- for y, has for equivalent
f^-AJ ^ Y + ^f^- V-etc..
i + yt i + y" 3
Vi + yi
of which the firstterm alone contains the simplepower of z, and there
its whole coefficient is
hj" J"
This then must be the sum of the
partialcoefficients of z found in (c).
That is -
= 1 -
2A^y + 3 A jf -
4A4y*+ etc.
But = 1 "
y + ?/2"
?/3-fetc. when y i" numericallyless than 1.

41. PROBLEM OF [log1 + a?]".
Hence 2AZ = 1, 3AZ = 1, = 1,or in generalAn = -
Finallythen,log(1+ y)=
y -
y^+ Jy8-
y*+ etc. . . .
while y2" 1.
N.B. This furnishes the means of computing logarithmsin
Elementary Algebra,before knowing the Binomial Theorem with
negativeor fractional exponent. If Differentiation or "Derivation,"'
as far as "f"(x)" xn, "fi(x)= nxn~l,be admitted,this equationat once
proves that when ""(z) means log(z),""'(z)= -
: a process which
eases the next Article.
10. PROBLEM. To develop[log.
1 +x]nin a series of powers of x.
That this is possible,when x2 is " 1, the precedingArticle shows.
We may then assume, with unknown coefficients X? ,
A"
,
A* . . . depend-ing
on n alone,where the upper index is not an exponent,
-
2 ...
w + r
+ etc
If = uny dz-nun~ldu, and
(a).
[It is
hardlyworth while to disguiseDifferentials by a more elaborate and
tedious Algebra.]
Differentiate both sides of (a),then dropthe common factor dx :
hereby,
n (log1 + XT'*_
-
Multiplyby 1 + x, and divide by n,
.-. (logf+^r1 = *"* -
*? "
;r
+ ^i
fe'tc----
-etc.
etc.
etc.
(6).
N.

42. 34 THE LAW OF Q SUFFICES.
But writing (n "
1) for n
in equation (a) we get
AT1.
Identifying (6) with (c), we
obtain X^w + XJ'1; and generally
XJ = (n + r -
1) x;_j + X?-1 or X?+1 = (n + r) X? + X?;}, the same law as
of
Q in Art. 4. Also evidently X" =
1 whatever n may be, as Q'j =
I.
Thus the top row
is 1. Again by (a) making n = 1,
XX lx*
But this is known to be x "
s? + J#3 "
x* + etc., whence
Thus the first column also of X
agrees
with that of Q. In short
then, the two tables are
the same. Finally :
(logl+aO* =
aft-
^^ +n
+
i'tt+2""tt 1 n + 2 n + 3
+ CiC'}
with coefficients already known.
The analogy to the series of Art. 8 deserves notice.
iv
"
rnu IM u*
(!^--i-l^+Jj^l5 I"NJ
..+et.

43. TRACT IV.
ON SUPERLINEARS.
SOME Apology may seem needful from me, since Dr Todhunter
in his volume on Higher Algebraic Equations has treated the same
subject under the name of "Determinants." Of course
I do not
pretend to add to him, nor indeed he to Mr Spottiswoode, who
carries off all merit on this subject. I read the details with much
admiration as treated by the latter, but found his notation by accents
very dazzling to the eye, in so much as to make it hard to know
by sweeping over half a page,
what was the meaning of the formula
presented to one. Also I found the chief strain in argument and
chief liability to error, to turn upon
the question, whether this or
that resulting term would require a plus or a minus. By reasoning
from linear functions in
my own way, though less direct, I was able
to avoid this danger and lessen fatigue to my
brain. When I ex-changed
words with
my
then colleague in University College,
London, the late Professor De Morgan, on
the question, why this
topic was not admitted into common Algebra, he replied, that it
was too difficult for beginners. I have since thought that he might
not have so judged, if some of the arguments were
otherwise treated;
and in fact I have found, that some
whom I supposed to speak with
authority thought my slight change of method easier to learners.
At the same time I must add, that on the very rare occasions in
which I have tried to teach an elementary class of mathematics,
a
mode of reasoning which to one pupil was easier, to another
seemed less satisfactory. Perhaps every
teacher ought to have "
two
strings to his bow."
3"2

44. BILINEAR TABLET
M N
P Q
1. Equations of the first degreeare called simple,but when
three or more letters (x,y, z...)are involved,complexityarises with
much dangerof error, even when there is no difficultyof principle.
To solve two equationsof the form alx + bly=
clt a"jB+ b$ =
c9 is
alwaysthe same process. If we could alwayscertainlyremember the
solutions
x =
y
and never confound the indices,nor mistake between + and "
,
this
alone might have much value. The modern method, due eminently
to the geniusof William Spottiswoode,is quiteadaptedto Elemen-tary
Algebra; but its vast range of utilitycannot there be guessed.
First study the denominator D =
alb2"
a,ib1.It arises from the
left-hand of the equation (alx+ bly=
c1, in which the four letters
stand in square, as Here D is the difference of the two
productsformed diagonally,and the diagonalwhich slopesdownward
from leftto rightis acceptedas the positivediagonal.This is a
cardinal point.Remember it,and you will not go wrong on + and "
.
Understand then, that in square with vertical sides
means MQ-PN.
,
which exchangesrows into columns.
M N
P Q
Of course then, so does M P
N Q
But ifyou change the order of the rows, or the order of the columns,
you change the result to PN"NQ, i.e.youinto P Q
M N
or N M
Q P
change D to " D.
After this is fixed in the mind, it is easy to remember the
common denominator above,viz.at"2"
a^, in the form Call
* "
it C. Then the numerator of x is obtained from C by changingthe
column ata2 into the column c^, making A =
So B for the numerator of y is found by changingthe column
bpt into c^, yieldingB =
a. c.
/ t
Finally,x=
"" , y= ,
without mistake.
V
C/

45. LINEAR FUNCTIONS. 37
Observe,if the equationsbe presentedin the form
aix + ty + c1= 0 ; a2x + bjj+ c2= 0 ;
this is equivalentto changing the signsof c1 and C2, which does not
affect C, but exactlyreverses the signsof A and B. Previously
we had
(x : A) =
(1 : C) =
(y : B),
or (x :
y : 1) =
(A : B : C) =
But from the two new equationsa:x + b$ + c^z=
0| you get
V + ty + c/
=
0|
= OJ
6. c. ci ai
C2 a2
a? : y : z =
in circular order.
We may also present the solution as follows :
M,
2. Simple equationsare often called Linear, by a geometrical
metaphor. If a quantityw is so dependent on x, y, z... that how-ever
the values of these may vary, yet always u = ax + by + cz -K . .
(where a, b,c... are numerical),then u is called a linear functionof
#, y, #... its constituents. [One might have expected u to be called
a dependentor a resultant : but for mysterious reasons of their own,
the French have adopted the strange word function ; and it cannot
now be altered.] It is convenient now to set forth a few properties
of linear functions. We here suppose the function to have no abso-lute
(constant)term.
I. To multiplyevery constituent by any number (m),multiplies
the function by that number.
[For,if u = ax + by+ cz+..., then
mu = amx + bmy + cmz +....]
II. If two linear functions have the same number of consti-tuents
and these have the same coefficients [as U=ax

46. T.EMMAS OX LINEAR FUNCTIONS.
Ut =
a.rt-f byi
4- cz{]; you will add the functions if you join the
constituents in pairs[forhere
U+l = u (./.-+ a-J+ b (y + y t)+ c (s+ *,);
whatever the number of constituents].
3. Observingnow that a M
b N
or aN " bM is a linear function
of X and J7",we see that to multiplya column MX by m multiplies
the function by m. Or ja, mM =
m a M .
Ib, wX b N
The same is true if we multiplya row ; for we may regard a and
M as the variables and b and N as constant ; then
ma, mM = m
b, X
This leads to the remark, that our function ought to be called
superlinearrather than linear ; for it is open to us to suppose con-stituents
alternatelyconstant or variable.
4. Next, by making a column or row binomial, we can some-times
blend two superlineartablets into one. Thus
a M
b N
A x
B y
G x
"" y ,
havingthe second column the same, yield,
(A y -
Ex) + (Cij- Dx )=
(A + C )y -
(B + L) x = A +"7,
y
Here the column which was in both, remains as before,but the
other columns are added and make a binomial. Evidentlythe same
process holds,if a row, instead of a column, is the same in both.
Conversely,when a givencolumn is binomial, we can resolve the
tablet into two tablets ; and when each column is binomial,we can
resolve the tablets into four.
Thus A+x, C .1, C! + z
B, D + v
x, C + z
y,
by " firstprocess. By a second, each of these tablets becomes two,
as result,
A C
11 1"
.1
/; H
x C
'/ l" H ''

47. VANISHING BILINEAR. 39
5. THEOREM. If one column (orrow) is identical with the other,
the tablet = zero. For obviously A A
,
by definition,is AB-BA
or zero. B B
COR. Equally the tablet =
zero, if one column (or row) be pro-portional
to the other. Thus if A : B = C : D, this proportion
yieldsAD = BO; hence
A C
B D
or A B
C D
,
meaning AD-BC, vanishes.
6. This sometimes usefullysimplifiesa tablet. Thus
is resolvable by Art. 4 into
A"mC, C
B " mD, D
A C
B D
mC, C
mD, D
But the second
tablet is zero, because its two columns are proportional.Hence the
given tablet simply == A C
B D
COR. Hence an important inference. The value of a tablet is
not changed if to one column (or row) you make addition propor-tional
to the other column (or row) ; nor again if you subtract instead
of adding.
Further, if in the originalequations of Art. 1, the absolute
terms c15 C2 become zero, the solution for x and y is simply x = 0 and
y = 0. This is indeed the only general solution, unless also the
denominator vanish ; which makes x "
^ , y =
^ ; deciding nothing
as to the value of x or y. In that case we can equate the two
i
values of ^ ; viz. -
= " -
a
-*
X
Conversely,this shows afa = aj)1
equivalent to = 0. The last is the condition which provides
that the two equations shall be mutually consistent,though x and y
do not vanish. It results from eliminatingx and y, leaving their
value arbitrary.

48. "tO TRILINEAR TABLETS.
7. Begin from the problem of three simpleequations,
[aBx+ b5y4- csz =
OJ
jese present three equationsto be fulfilled by only two disposable
/v" /iy
quantities,viz. - and -
,
if they are all divided by z. The three
equationsare not certainlyself-consistent. If #, y, z be eliminated,
an equationof condition will remain. Our first business is to in-vestigat
it.
From the two firstequationstreated as at the end of Art. 1,but
abandoningcircular order,we have
in which "
In the third givenequation,substitute for xyz the three quantities
now provedproportionalto them, and you get
(1) -fc a, c. 0.
Call it F3= 0. Then F3 is linear in aj)9cs.This is the condition
that the three equationsshall be compatible. It is seen to result
from eliminatingx, y, z. Professor De Morgan wished to call these
tablets Eliminants. Why Gauss entitled them Determinants,no one
explains.Spottiswoodeapparentlyintroduced the excellent notation
at bl cl Then Fn is linear in a8, 63,c3,that is,
(2) F3 =
a2 62 C2 in its third row. Hence also in any row.
as fy"c" ^3 ^s superlinearof the third order.
for the value written above. The coefficient of aa is obtained in (1)by
obliteratingthe constituents as last written that are in the same
column or row as aa, thus reducingF8 to
then we see the t.-ihk-tl"v liirli,/.. rnust !)""multiplied.

49. EXPANSION OF A TRILINEAR. 41
The same process is used with 63and c3,producing
...
c.
and
Finallythe signsof the terms of V3 are alternate
aj)2"
justas in the bilinear
Evidently F3 is formed of six terms, three positiveand three
negative; each term having three factors,but in no term is any
factor combined with another of its own row or its own column.
In c0 the term aj)2c3(the diagonal slopingdown from
leftto right)is positiveas before. Thus when F3 is given in con-tracted
form, we can expand it into three apparent binomials.
8. In the three given equationsyou may exchangethe position
of x and y ; then by eliminatingy, x, z you obtain
an ca
= 0;
but you cannot infer that U3=
F3. In fact,to exchangethe a column
with the b column reverses the signof
,
62
.
Thus it changesF3 into
6,0,
That is,to exchange the first and second columns justreverses the
signof F3. The same effect follows from exchangingany two con-tiguous
columns or rows. Thus generally
Again,

50. "1 EXCHANGE OF COLUMNS OR ROWS.
Observe,that if three binomials of V3 are expressedby
maa + H-cra4- pal
the multipliersmt n, p contain nothing of the column a1? a2, a3,
therefore V3 is linear in these three constituents. Evidentlyit is
linear in regardto any column ; as we before saw, as to any row.
9. THEOREM. Further, 7 say, To exchange rows and columns
does not alter the value of V3. In proof,multiplythe three equations
givenin Art. 7,by disposablenumbers m, n, p, and so assume m, n, p
that when the three productsare added togetherthe coefficients of y
and z may vanish. There will remain (ma^+ ?ia2-f pa3)# = 0, and as
we do not admit #=0, we have three equationsconnectingm, n,p viz.
a,m -I-a2?i+ a 3p = 01
Ji7H+ "g?l_l_])^p=o'
cjn + c.2n-f C3p =
OJ
and that these may be compatible,we need
k o,
Cl C2 "
by eliminatingm, n, p.
Here S3 is nothing but V3 with rows changed to columns and
columns to rows, retainingthe same positivediagonalaj)2c3.Every
learner will easilyfind by developingV3 and S3that theyare identical:
but there is an advantage here in generalargument applicableto
higherorders. $3= 0 and V3= 0,beingeach a condition of compati-bility
of the previousequations,must contain the same relation ofthe
constituents. S3 is a linear function of its column aj)^ ; so is V3 a
linear function of its row ajb^. But $3= 0, Fa= 0 being derivable
one from the other, there is no possiblerelation but $3=
/z V3 in
which n must be free from a^Cj. But the same arguments will prove
that p is free from a262c2,also from a3b3c3.Therefore /-t is wholly
numerical. Make 6,= 0, ct= 0 and this will not affect ft. But this
makes
and S =
M.
But that the two minor tablets are identical was implied in their
definition. Hence, on this assumptionfor bland c,, we find F3 =
A
or /Lt= l. This then is the umuersal value of /^ ur F;!=
#, in all
"". i-;.I).

51. ON A SUPPLEMENT VANISHING. 43
10. In the developed value of F3 (Art. 7) if 63= 0 and
c3 = 0,
you get simply F3 =
as 64c, which does not contain av or az. These
two constituents are made wholly inefficientby the vanishingof b3
and
c3, and
may be changed to zero. Thus
0 0 a 0 0
So *"**
""
When a major square is divided into two minor squares and two
complemental rectangles,the vanishing of one rectangle obliterates
the other, and the greatest tablet has only the two squares for its
factors.
11. Since F3 is a linear function of every row and of every
column, we can
argue as in the Second Order or Bilinears,that to
multiply any column, or any row, by m, multipliesF3 by m ; and if
a column or row consist of Binomials, we resolve the tablet into two.
Converselytwo F3s which differ only in a singlerow or singlecolumn
can be joined into one universally,
A+m, A' A0
B + n, B' B0
C
A A' A,
B Bf B0
G C' Cn
mA' AQ
n B' B0
P C' CQ
12. Further, if two contiguous columns (or rows) be identical,
the F3 = zero. For to exchange them changes F3 to -
F3. Yet the
exchange leaves F3 exactly what it was before. Hence F8 = "
F8.
This can only be when F3 = 0.
It follows that if a column (orrow) be proportionalto a contiguous
column (or row), the tablet is zero. For instance, if
av bv ct are pro-portional
to a,2,62,c2, we may assume ax =
wa2, 6t=
mb.2,cl =
??ic2,then
rac
This gives a2 62c,

52. 44 TO SOLVE FOR X, y, Z IN SIMPLE EQUATIONS.
and the last tablet is zero, because its first and second row are
identical.
What has been said in this Article of two contiguous rows or
columns is evidentlytrue of any two rows or any two columns, since
exchange of contiguous rows (or columns) does but multiply the
tablet by - 1.
13. The same argument as before in the Second Order now
proves that a tablet V3 is not changed in value, if any row (or
column) receives increase or decrease proportionalto some other
row (or column). Thus we have shown in V3 the same propertiesas
those enunciated in F2.
14. NEW PROBLEM : to solve for x, y, z in the three equations
ai" + b + cz + d = 0,
2
= 0,
Assume d,=
Ajc, d2= A^x, d3= A3x. Then
Eliminate the x, y, z here visible;then
= 0.
The last tablet may be resolved into two, namely:
a, I,c,
0.
Multiplythe former of these by x, and, as an equivalence,multiply
each constituent of the first column of the latter by xt
a

53. THE PROBLEM SOLVED. 45
In the first column of the last restore for Ajc, Ajc, Aax their
values dv d2,ds. Then if
you have Dx + = 0,
which solves for x. By perfectlysimilar steps
at b,dla, dl Cl
0; = 0.
These are easy to remember: each suggests the other, by entire
symmetry. The method succeeds in Higher Orders.
COR. If we make x =
-, y = -
,
z = -
,
Then from
you obtain the proportion
= a
Ifi= 0.
-Dz =
" : * : f
"3 C3 ds
15. PROBLEM. To eliminate x from the two equations
(px2 + qx +r* =0)
where P} Q, R, p, q, r may involve y or other quantities.First,put
x2 = X, then we have
pX + qx + r = 0
Eliminate X i.-e.solve for x;
= 0 .(1).

54. TWO PROBLEMS OF KL1MINATION.
Again,writingin the original
'(Pa;+ Q) x + R =
0]
(px 4- q)x 4- r = Oj
eliminate .r,as if P,r + Q and px + q were ordinarycoefficients. Then
Px + Q, R
px + ,
r
which expanded,gives
PxR + QR
px r q r
= 0, or PR
p r
x + QR
" r
Eliminate x between (1)and (2),which gives
that is,
the result required.
2_
= 0,
16. PROBLEM. To eliminate x from the two equations,
few;3+ Sbx* + Bex + d = 0,
ax*+2bx+c = 0.
First,multiplythe last by x and subtract ;
Compare the two last with the two equationsof Art. 15,
/. P =
a, Q = 2", R =
c, p = b, q = 2c, r = d.
Hence the elimination of x yields
a 2b
b 2c
2bc
2c d
a c
b d
2=0, or ab
b c
be
c d
= a c
b d
This is the condition of two equalroots in the givencubic.
17. By conductingelimination from three givensimpleequations
by a second process, we attain relations which were not easy to
-"niticipate.Assume the three "".jiiationsof Art. 7. Kliminatc //

55. AN IDENTICAL EQ. BETWEEN 9 CONSTITUENTS, ALL ARBITRARY. 47
twice,(1)from the two first;(2)from the second and third. Hence
we get
x =
from which, by eliminating#, we obtain U= 0, if we define U by the
equation
aa ba
But, otherwise eliminated,we find,as the condition of compatibility
F3 = 0.
Therefore "7=0 contains the same relation of the constituents as
F3 = 0. By inspection,we see that U, equallywith Fs, is linear in
a,, 6j,cr Since then ?7 and F vanish together,we have necessarily
U=fj,.V3,in which yu,does not involve alt b1nor cx. To determine /i,
suppose at = 1, 6X= 0, Cj= 0
,
c2 = bn ba
and 100 100 ",',
O^a
so that in this particularcase U= 62F3,or /-t=
52. This then is the
value of //,for all values of altbiycltor universallyU=bz. F3, while
all the nine constituents are arbitrary. Q.E.D.
18. To remember this important equation,write the square
trilinear largerand mark out its minor square. The factor b2is in
the centre.
'2 " '
3-
By interchangingrows or columns without alteringthe value of
F3, fresh relations are obtained. Indeed no one constituent can
claim the central placefor itself.

56. QUADRILINEAR TABLET.
Fourth Order.
19. To eliminate x, y, z, u from four givenequationseach of the
form a^x 4- b$ + ctz 4 dtu= 0, we have now much facilityfrom the
Cor. to Art. 14. First, eliminate from the three first equations
and get the proportionsof x, y, z, u. Next, insert these propor-tionate
values in the fourth equation whereby you entirelyeliminate
all the four,and obtain an equationF4= 0 ; if F4 stand for
6, c, dt
This developedform of F4 can alwaysbe recovered (by attention
to the simple rule given for developingF3) from the conciser or
**ttdevelopedform
Evidentlyin the definition F4 is a linear function of a4 64c4 d^.
So then it must be of any other row, the order of the given
equationsbeing arbitrary. Also the firstterm of F4 as defined is
free from a/y^; each of the others is linear in a^a^ Therefore
F4 in square is linear as to its first column ; so then must it be
as to every column.
Being thus linear,if one column (or row) of such quadrilinear
tablet is binomial, it may be splitinto two tablets by the same
process as in the third order. Likewise to multiplyany column
(orrow) by m multipliesthe whole tablet by m.
To exchange first and second column, exchanges the first and
second term of F4, but reverses their signs. It reverses the sign
of the third term, also of the fourth. Thus to exchange the firstand
second column reverses the sign of F4. Evidentlythen the same
must happen by exchanging any two contiguouscolumns. The
same argument appliesconcerningany two contiguousrows.
The reasoningof Art. 12 concerningF3 now appliesto F4,
showing that the tablet vanishes, if one column (orrow) be pro-

57. ITS PROPERTIES THE SAME. 49
portionalto another column (orrow). From this it further follows
(as concerningF3 in Art. 13, and concerningF2 in Art. 6), that.
F4 is not changed in value, if any row (or column) receive iner
or decrease in proportionto some other row (orcolumn).
20. That F4 is not altered by exchangingrows and columns,
is generallyproved by elaborate inspectionof the separate terms
when F4 is resolved into 24 elements each of the form a1b^c^d4,no
two factors of the same row or column, and showingthat the + or -
of the term is never altered. It is,no doubt, a perfectdemonstration,
and more elementarythan mine ; but I find the less obvious ar-gument
of Art. 9 the easier for all the higher orders. Multiply
the given equationsby 'inl^lplqi and assign to these multipliers
the condition that from the sum of the equationsthus multiplied
y, z and u shall disappear.
There will remain (mal+ na^-}-pa9+ qaj x = Q. But our hypo-thesis
forbids # = 0, hence we have four equationsto determine
tnnpq, viz.
+ aji + a3p + a^q = 0,
bjn + b2n+ b3p4- b4q= 0,
Cjiw.+ czn + c3p + c4"/= 0,
djm,+ dzn+ d3p + d4q= 0.
When we eliminate mnpq the result,which we may call S4= 0,
shows $4 differingfrom F4 only in the exchange of rows with
columns. Each of them is linear in ap^^. Each involves the
same relations between the constituents. The equation$4= 0 must
be deducible from F4 = 0. The only possiblerelation,making S4
and F4 vanish together,has the form $4= yu,F4,in which /z
is inde-pendent
of "VWV But symmetry proves p equallyindependent
of every other column; therefore p is numerical. To find it,we
may make the constituents on the positivediagonalall = 1, mM
all the other constituents vanish. Then both $4 and F4 =
at6sc3rf4- 1 .
Universallythen, /a = l, or S4=F4. Therefore F4 is not all
by exchanging rows with columns.
Evidently this argument holds, however high the order of the
Tablet if the successive definitions follow the same law.
*

58. 50 SOLUTION OF FOUR SIMPLE EQUATIONS.
21. We can now solve when four given simple equationscon-necting
xyzu have on the left side absolute terms e1e2e3e4,with zero
(asbefore)on the right. We proceed as in Art. 14. Let
el = A jflj, e2=
Then our equationbecomes
9x, e4 =
A4cc.
u = 0
(a4+ A4) x + b4y+ C4z + d+u= 0
Eliminate x, y, z, u, then
blCl
.
"4 C4
The first column being binomial, we can resolve this tablet into
two. Then multiplythe left tablet by x, and the first column of
the second also by x ; whence
A 1
Cj
0.
c*
In the second tablet we now replaceits column by its value
0te,e,04.
Thus we have solved for x. By perfectlysimilar steps we
solve for yt for zy and for u.
Finally,if
M= """
,
N=
,
P =
i"4c4 dt e4 a4 c4 c?404
^i c.
Q= ,
R =
a,
we have x : y : z : u : 1 = M : " N P : "
Q : R.

59. COMPLEX DELATION LT =
(6.(C3-
bnc) V 51
22. Take our four equationsas in Art. 19. From the three first
and also from the three last eliminate both y and z ; whence
b c
; and
To eliminate x from these two, we have
a, 6. "
U=0
which we may remember by
Thus f/"4= 0 and F4 = 0 express the same condition of the con-stituents
for reconcilingthe four equations.
Inspectionshows that "7"4,like F4, is linear in ajb^d^ Put
C/4=
yLtF4,and //. will be free from these four. Assume then al = l,
*)
= c =
d = 0. and it will not affect u,. But it makes
111^
and U4= 1
that is,
whence f/"4generally .
F.. This could not have been fore-seen.
By varyingthe order of the elements,we have other results.
4"2

60. GENERALIZATION OF THESE PROPERTIES
Observe that is the square in the centre of V4. The tri-
linears in ?7are squares cut from the four corners of F4; those of the
firstterm in U4 beingfrom the positivediagonal.
23. By aid of Art. 21 we readilyproceed to the Fifth Order,
with the same law of continuous formation; whence in every Order
we have these same properties.
(1) To exchange rows and columns does not affect the value
of T..
(2) Fn is a linear function of any one row, or any one column.
(3) If a row or column be binomial, the Fn may be splitinto
(4) To multiplya row or column by m, multipliesFn by m.
(5) To exchange any row (orcolumn) with a contiguousrow (or
column) changes Fn to "
Fre.
(6) If one row (or column) is identical with or proportionalto
another row (orcolumn), the Fn = zero.
(7) Fn is not altered in value when a row (orcolumn) receives
increase or decrease proportionedto another row or column.
(8) If Fn be divided along the diagonal,so as to fall into four
parts,two squares and two rectangularcomplements, the vanishing
of one complement makes the other wholly ineffective.
24. To prove the last universally,it suffices to prove it for the
fifth order.
Call the two squares P, S and the complements Q, R. Then if
one of the complements,as Q, hav"- :"11its constituents zero, I say,
R is ineffective,and F=P .
S, justas if R also had all itsconstituents
zero. For every term of FB when fullyexpanded,has the form
ajbncpdqer,where mu/n/r an-, taken from I, '2,:",I, 5 and no two are
the same. Hence ajb4c4and "66ftcfi(the constituents of R) are neces-
snrilymultipliedby one or nih"T ,,f il 'l.cjlf.^in Q, mid

61. FOR ALL ORDERS.
all the products vanish. Consequently, if P is of the third order and
S of the second, the F in question is equivalent to
0 0
a2 "2 c2
00
a.
6. c.
00
000
000
and might arise from two equations separately, yielding P = 0, and
If Spottiswoode did not plant the first
germ
of this
very
valuable
theory, he first investigated the laws and exhibited its vast
power.

62. TRACT V.
INTRODUCTION TO TABLES I. AND II.
To these four Elementary Tracts I have added two Numerical
Tables, solely because their compilation and verification is elemen-tary.
Table I. gives values of A~" to 20 decimal places. Here A means
the series 2, 3, 4, ... up to 60, and the odd numbers from 61 to 77;
and n means 1, 2, 3, ...
continued until A~n is about to vanish. To
verify,use the formula
The reader may convince himself how searching is this test, by
applying it, for instance, to A"11 when A =
37 or when A =
71. Only
in the case of 2~n and 3~n, where the Tablets give only odd values of
n, we must apply the formula
A "
A ~2m~1
(A~l + A~3 + A~5 + ...
+A-*m~l) = ~
,
.
A. " 1
Table II. has values of xn with 12 decimal places, where x means
"02, '03, '04 up to '50 and n is continued from 1, 2, 3,... until xn is
insignificant. The formula of verification is (with ra any integer less
than r)
(at*+ xm+l + aT" + . . .
+ O .
(1 -
x) = x" -
af* '.
I compiled this table while working at Spence's integral
0
but it has much wider use.
One who is sagely incredulous of printed tables can verity
fur himself any tablet which he is disposed to use with much greater
ease than he could
compose the tablet. Thus, too, he would dct" "" -t
jury error fn"m muCOpying or misprinting, against which I can leasl
give a L,ri"

63. TABLE I. TWENTY DECIMALS. 55

64. TAl'.I.K I. TWENTY DECIMALS.

65. TABLE I. TWENTY DECIMALS.

66. TABLE I. TWENTY DECIMALS.
For i6~" look to 4
*

67. TABLE I. TWENTY DECIMALS. 59

68. 60 TABLE I. TWENTY DECIMALS.
For 25
"
look to 5 2".

69. TABLE T. TWENTY DECIMALS. Gl

70. 62 TAl'.T.K I. TWENTY DECIMALS.
35-" 37"
i
2
3
4
6
7
8
9
10
ii
12
13
'02857 14285 71428 57142
81 63265 30612 24489
2 33236 i5l6o 34985
6663 89004 58142
190 39685 84518
5 43991 02415
J5542 60069
444 0743"
12 68783
36251
1036
29
i
2
3
4
6
7
8
9
10
ii
12
"02702 70270 27027 02702
73 04601 89919 64938
i 97421 67295 12566
5335 72089 05745
144 20867 27182
3 89753 16951
10533 86945
284 69917
7 69457
20796
562
For 36"" look to 6'

71. TABLE I. TWENTY DECIMALS.

72. (54 TAl'.LE I. TWENTY DECIMALS.

73. TABLE I. TWENTY DECIMALS.
For 49
"
look to 7'

74. 66 TABLE I. TWENTY DECIMALS.

75. TABLE I. TWENTY DECIMALS. 67
i
2
3
4
6
8
9
10
63-
"01587 30158 73015 87301
25 19526 32905 01385
39992 48141 34942
634 80129 22777
10 07621 09885
15993 98569
253 87279
4 02973
6396
101
i
2
3
4
6
7
8
9
10
"01538 46153 84615 38461
23 66863 9"532 54438
364J3 29085 11607
56" 20447 46333
8 61853 03789
27751
203 98888
3 J3829
4828
75
5"2

76. 68 T.vr.LE I. TWEXTY DECIMALS.

77. TABLE II. TWELVE DECIMALS. 69
TABLE II. Powers of -02,-03,-04,...
up to -50,useful to compute
A3a?+ "c.,when x does not exceed J.
(Twelve Decimals.)

78. TABLE II. TWELVE DECIMALS.

79. TABLE II. TWELVE DECIMALS.

80. 1-1 TABLE II. TWKLVE DECIMALS.

81. TABLE II. TWELVE DECIMALS. 73

82. 74 TABLE 11. TWELVE DECIMALS.

83. .
TABLE II. TWELVE DECIMALS. 75

84. 76 TABLE II. TWELVE DECIMALS.

85. TABLE IT. TWELVE DECIMALS. 77