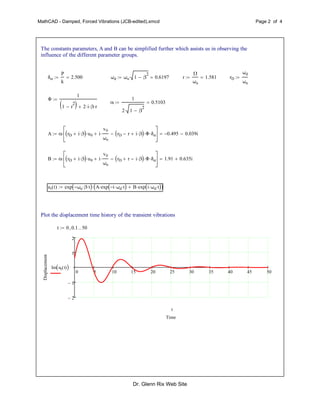
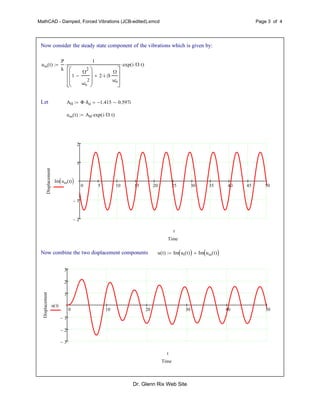
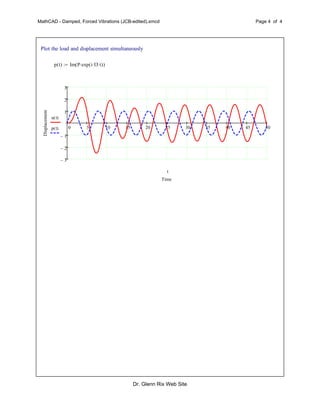
This document analyzes the damped, forced vibrations of a mass-spring-damper system. It specifies the system parameters and derives equations to describe the transient and steady-state responses. The transient response is a combination of decaying exponential terms, while the steady-state response is a sinusoid at the driving frequency. Plots show the displacement over time for the transient and steady-state responses separately, and their combination. A final plot shows the displacement and driving force versus time.

1. MathCAD - Damped, Forced Vibrations (JCB-edited).xmcd Page 1 of 4
m
k c
Pei t
( )u t
Damped, Forced Vibrations
Specify the initial displacement and velocity of the mass
Initial displacement u0 0.0
Initial velocity v0 0.0
Specify the stiffness, mass, and fraction of critical damping
k 0.4 m 1 β 0.20
Specify the amplitude and circular frequency of the load
P 1.0 Ω 1.0
First consider the displacement time history of the transient vibrations:
ωn
k
m
0.6325
A
i ωn β ωn 1 β
2




 u0
2 ωn 1 β
2

i v0
2 ωn 1 β
2


i ωn β ωn 1 β
2
 Ω




2 ωn 1 β
2

P
k

1
1
Ω
2
ωn
2
 2 i β
Ω
ωn


A 0.495 0.039i
B
i ωn β ωn 1 β
2




 u0
2 ωn 1 β
2

i v0
2 ωn 1 β
2


i ωn β ωn 1 β
2




 Ω




2 ωn 1 β
2

P
k

1
1
Ω
2
ωn
2
 2 i β
Ω
ωn


B 1.91 0.635i
Dr. Glenn Rix Web Site

2. MathCAD - Damped, Forced Vibrations (JCB-edited).xmcd Page 2 of 4
The constants parameters, A and B can be simplified further which assists us in observing the
influence of the different parameter groups.
δst
P
k
2.500 ωd ωn 1 β
2
 0.6197 r
Ω
ωn
1.581 rD
ωd
ωn

Φ
1
1 r
2
  2 i β r

α
1
2 1 β
2

0.5103
A α rD i β  u0 i
v0
ωn
 rD r i β  Φ δst






 0.495 0.039i
B α rD i β  u0 i
v0
ωn
 rD r i β  Φ δst






 1.91 0.635i
ut t( ) exp ωn β t  A exp i ωd t  B exp i ωd t  
Plot the displacement time history of the transient vibrations
t 0 0.1 50
0 5 10 15 20 25 30 35 40 45 50
2
1
1
2
Time
Displacement
Im ut t( ) 
t
Dr. Glenn Rix Web Site

3. MathCAD - Damped, Forced Vibrations (JCB-edited).xmcd Page 3 of 4
Now consider the steady state component of the vibrations which is given by:
uss t( )
P
k
1
1
Ω
2
ωn
2









2 i β
Ω
ωn









 exp i Ω t( )
Let AH Φ δst 1.415 0.597i
uss t( ) AH exp i Ω t( )
0 5 10 15 20 25 30 35 40 45 50
2
1
1
2
Time
Displacement
Im uss t( ) 
t
Now combine the two displacement components u t( ) Im ut t( )  Im uss t( ) 
0 10 20 30 40 50
3
2
1
1
2
3
Time
Displacement
u t( )
t
Dr. Glenn Rix Web Site

4. MathCAD - Damped, Forced Vibrations (JCB-edited).xmcd Page 4 of 4
Plot the load and displacement simultaneously
p t( ) Im P exp i Ω t( )( )
0 5 10 15 20 25 30 35 40 45 50
3
2
1
1
2
3
Time
Displacement
u t( )
p t( )
t
Dr. Glenn Rix Web Site