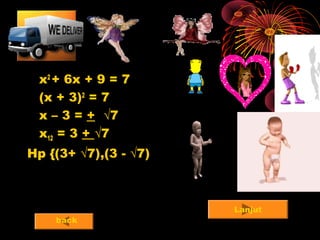
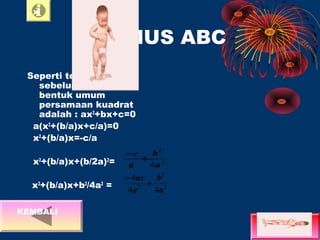
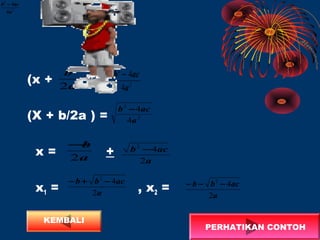
Dokumen tersebut membahas tentang persamaan kuadrat, mulai dari bentuk umum persamaan kuadrat, cara-cara menyelesaikan persamaan kuadrat meliputi memfaktorkan, melengkapkan kuadrat sempurna, dan menggunakan rumus abc, diakhiri dengan contoh soal latihan.