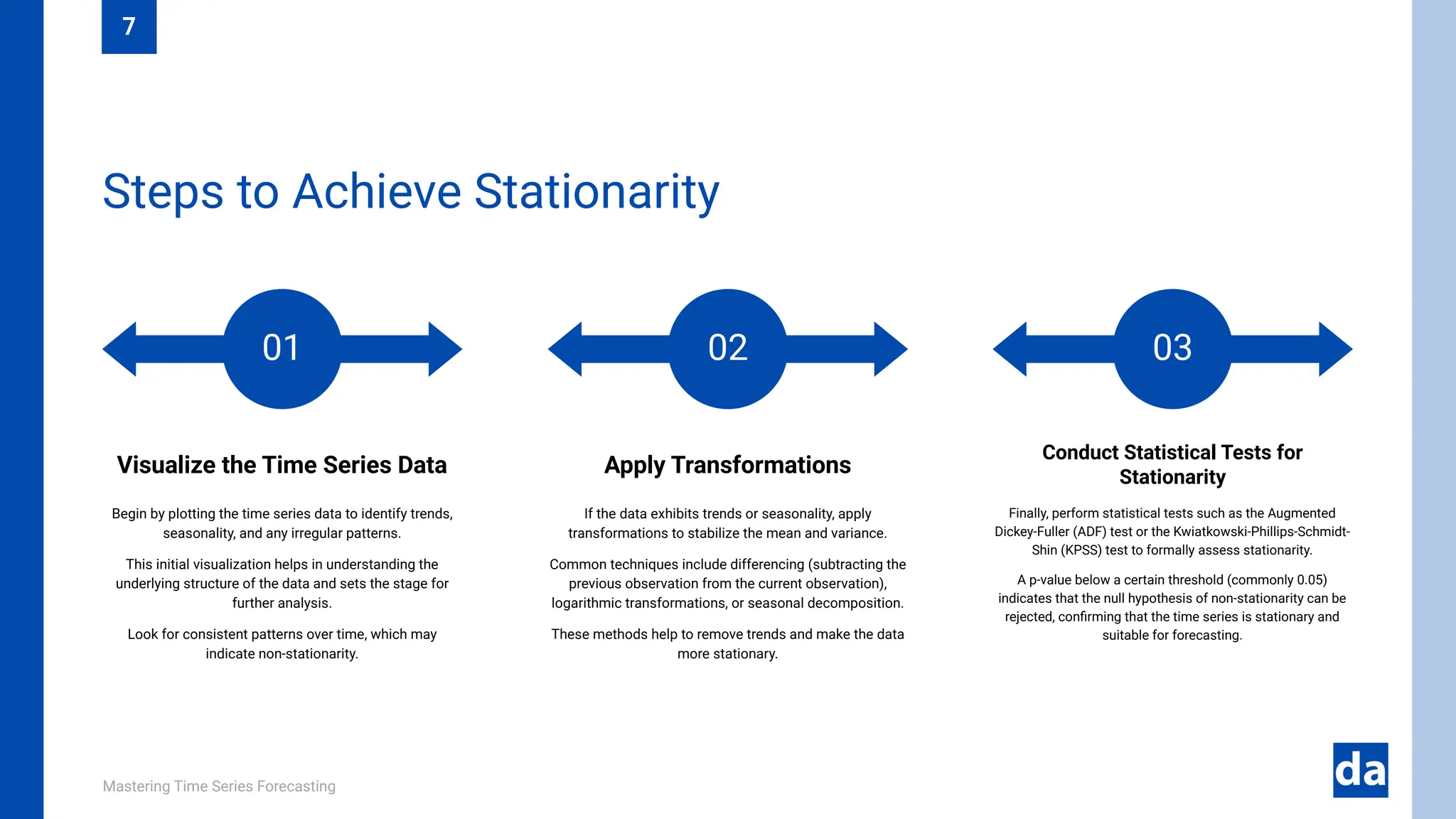
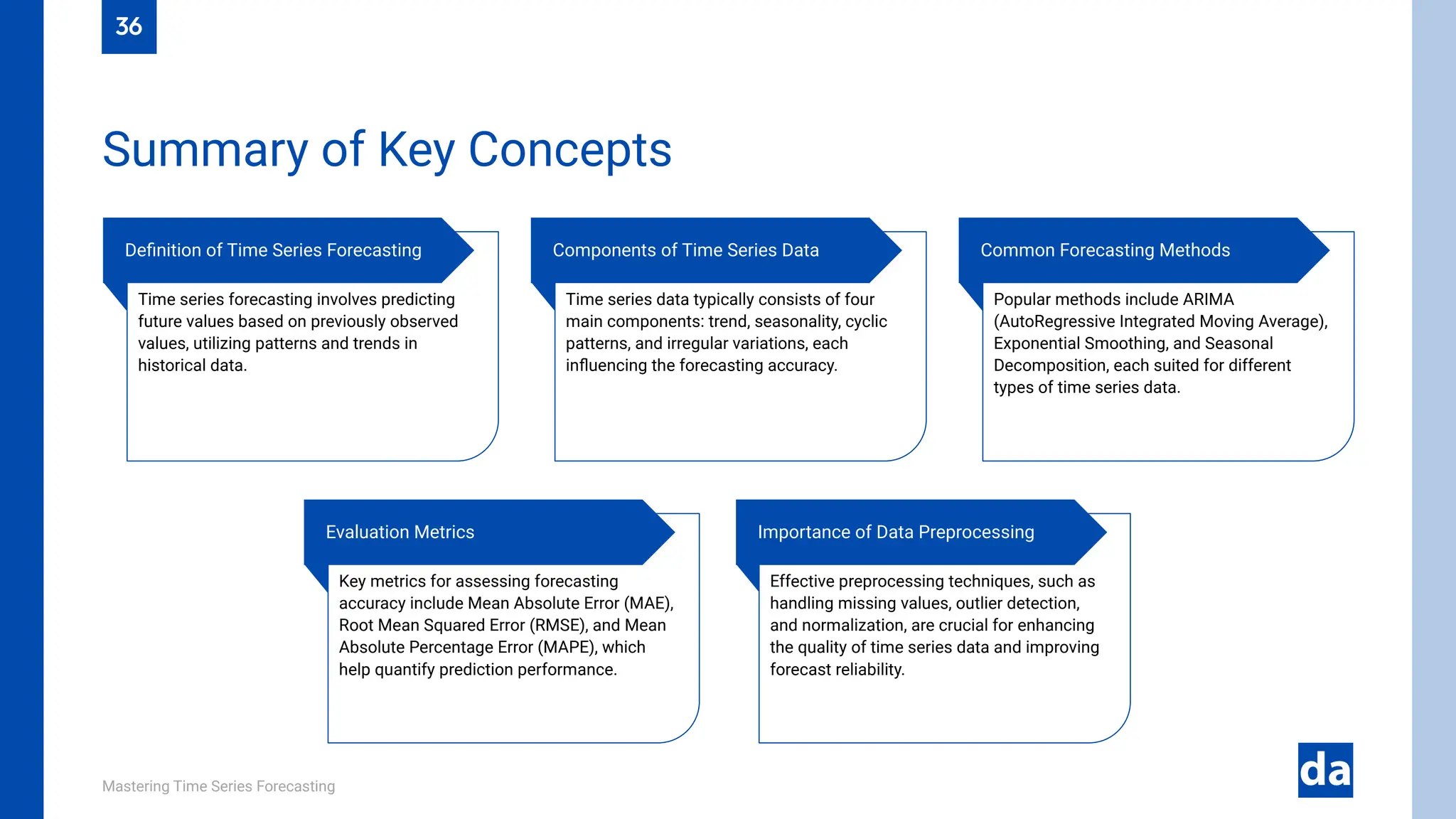
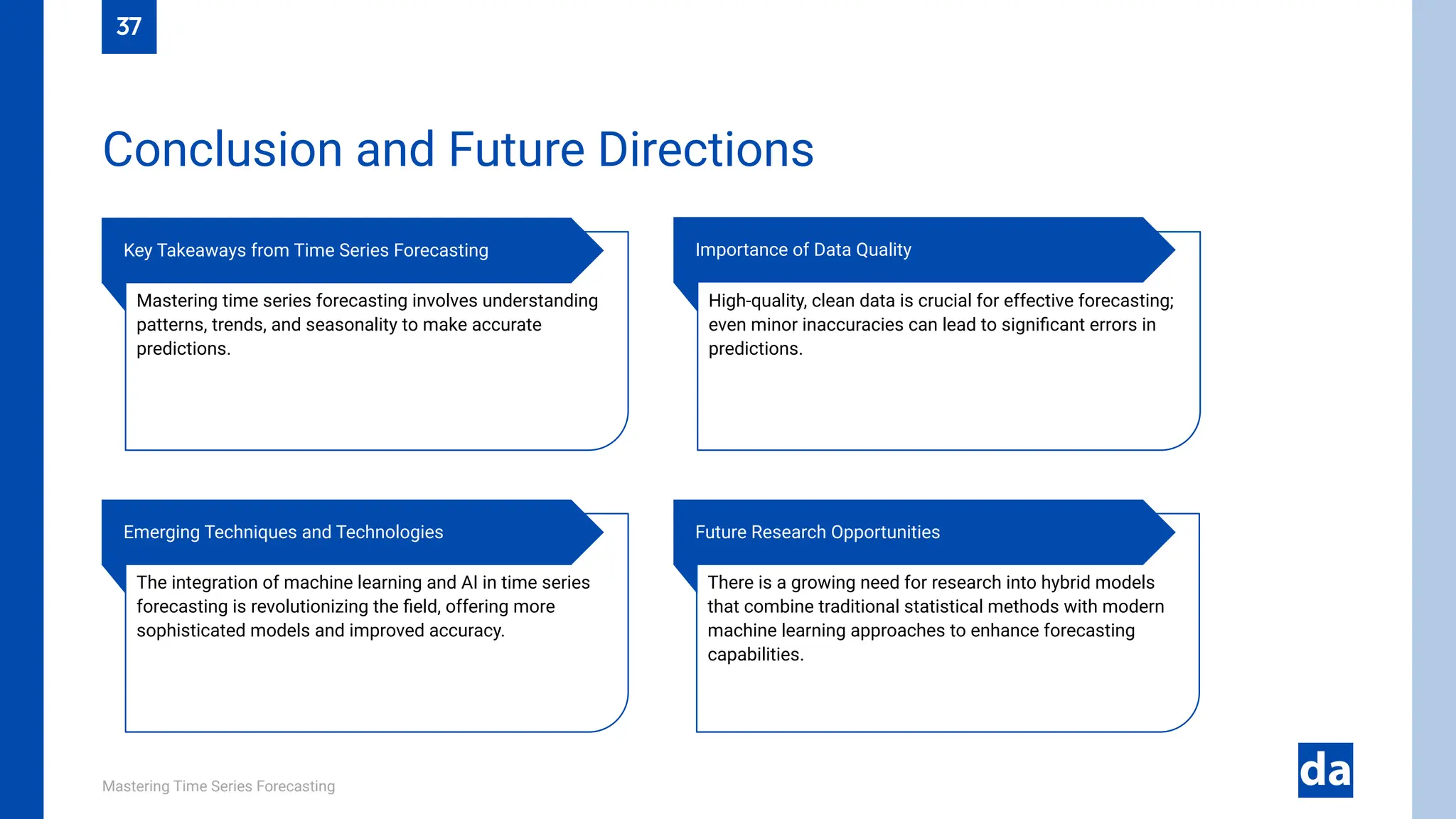
The document serves as a comprehensive guide to time series forecasting, covering techniques, applications, and future trends. It details the importance of time series analysis, types of data, various forecasting methods including ARIMA, SARIMA, and machine learning approaches like LSTM, and evaluation metrics for accuracy. Additionally, it discusses real-world applications in sectors such as finance, healthcare, and retail, as well as challenges and future trends in the field.