Downloaded 128 times
Uploaded byAnant Agarwal
Machine Learning for Forecasting: From Data to Deployment
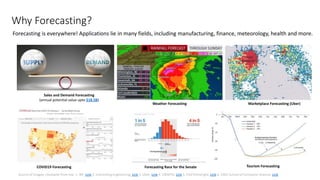
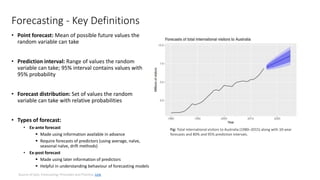
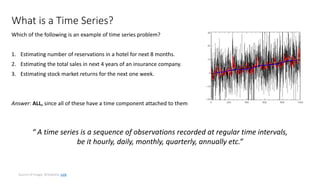
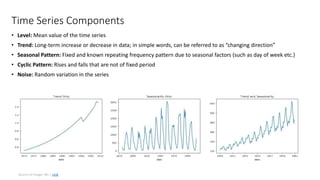
The document presents a comprehensive overview of using machine learning for forecasting, emphasizing the significance of time series analysis, feature engineering, and various machine learning techniques. It discusses best practices for data governance, forecasting accuracy determinants, types of forecasts, and the importance of model evaluation and deployment strategies. Additionally, it includes a tutorial on deep learning with TensorFlow and highlights the applications of forecasting across various industries.
More Related Content
Similar to Machine Learning for Forecasting: From Data to Deployment
Machine Learning for Forecasting: From Data to Deployment
- 1. Machine Learning forForecasting: From Data to Deployment Anant Agarwal Lead Data Scientist Nissan Motor Corporation ZJU Earth Data Program
- 2. Education Current Role Previouslyassociated with High School B.S. and M.S., Geology M.S., Geophysics, Scientific Computing About Me Lead Data Scientist, Global Digital Hub
- 3. Agenda • Introduction • Understandingtime series • Feature engineering and EDA • Machine learning • Tutorial on Deep Learning with TensorFlow
- 4. Agenda • Introduction • Understandingtime series • Feature engineering and EDA • Machine learning • Tutorial on Deep Learning with TensorFlow
- 5. Source of image,The Economist, Link
- 6. Source of image,XKCD, Link Data - Best Practices: • Structured data systems instead of manual preparation and maintenance of data files • Data governance (the who-what-how-when-where and why of data) • More inter-connected data teams for increased collaboration and richer data sources Data “We don’t have better algorithms…we just have more data.” - Peter Norvig, Director of Research, Google
- 7. What is DataScience? Twitter definitions circa 2014. • A data scientist is a statistician who lives in San Francisco. • Data Science is statistics on a Mac. • A data scientist is someone who is better at statistics than any software engineer and better at software engineering than any statistician. Source of images, from left to right. 1. The Data Scientist magazine, Link 2. Sketchplanations, Link 3. Map of data science by Cassie Kozyrkov, Link
- 8. Example adapted fromCassie Kozyrkov’s article “When not to use ML or AI”, Link No pattern connecting inputs to outputs: The problem is defunct/not solvable If there is a pattern: Machine learning can help us (given the existing conditions only slightly change or continue) Machine Learning “Machine learning is an approach to automating repeated decisions that involves algorithmically finding patterns in data and using these to make recipes that deal correctly with brand new data.” Finding patterns Ability to generalize well Dosage for Day 2? Dosage for Day 61? Just look up the table! Machine learning can help here.
- 9. Forecasting is everywhere!Applications lie in many fields, including manufacturing, finance, meteorology, health and more. Sales and Demand Forecasting (annual potential value upto $18.5B) Weather Forecasting COVID19 Forecasting Marketplace Forecasting (Uber) Forecasting Race for the Senate Why Forecasting? Tourism Forecasting Source of images, clockwise from top. 1. IBF, Link 2. Interesting Engineering, Link 3. Uber, Link 4. UNWTO, Link 5. FiveThirtyEight, Link 6. CMU School of Computer Science, Link
- 10. The below factorsdetermine the accuracy of the forecasts: 1. Our understanding of the factors that affect the target variable 2. Availability of data 3. Whether the forecasts have a direct effect on the thing we’re trying to forecast What can be forecasted? Source of images, from left to right. 1. Link 2. Link
- 11. Our understandingof the factors that affect the target variable Availability of data Whether the forecasts have a direct effect on the thing we’re trying to forecast What can be forecasted? Source of images, from left to right. 1. Link 2. Link Highly accurate!
- 12. 1. Our understandingof the factors that affect the target variable Availability of data 3. Whether the forecasts have a direct effect on the thing we’re trying to forecast What can be forecasted? Source of images, from left to right. 1. Link 2. Link Not Accurate (50-50 chance)!
- 13. Forecasting - KeyDefinitions • Point forecast: Mean of possible future values the random variable can take • Prediction interval: Range of values the random variable can take; 95% interval contains values with 95% probability • Forecast distribution: Set of values the random variable can take with relative probabilities • Types of forecast: • Ex-ante forecast Made using information available in advance Require forecasts of predictors (using average, naïve, seasonal naïve, drift methods) • Ex-post forecast Made using later information of predictors Helpful in understanding behaviour of forecasting models Source of plot, Forecasting: Principles and Practice, Link Fig: Total international visitors to Australia (1980–2015) along with 10-year forecasts and 80% and 95% prediction intervals.
- 14. Agenda • Introduction • Understandingtime series • Feature engineering and EDA • Machine learning • Tutorial on Deep Learning with TensorFlow
- 15. What is aTime Series? Source of image, Wikipedia, Link Which of the following is an example of time series problem? 1. Estimating number of reservations in a hotel for next 8 months. 2. Estimating the total sales in next 4 years of an insurance company. 3. Estimating stock market returns for the next one week. Answer: ALL, since all of these have a time component attached to them “ A time series is a sequence of observations recorded at regular time intervals, be it hourly, daily, monthly, quarterly, annually etc.”
- 16. Time Series Components Sourceof image, ML+, Link • Level: Mean value of the time series • Trend: Long-term increase or decrease in data; in simple words, can be referred to as “changing direction” • Seasonal Pattern: Fixed and known repeating frequency pattern due to seasonal factors (such as day of week etc.) • Cyclic Pattern: Rises and falls that are not of fixed period • Noise: Random variation in the series
- 17. Time Series Components Sourceof image, Forecasting: Principles and Practice, Link Can you identify the patterns present in the time series? Strong yearly seasonality Strong cyclicity with period of 6-10 years Downward trend
- 18. Time Series Components Sourceof image, Forecasting: Principles and Practice, Link Can you identify the patterns present in the time series? Strong seasonality Strong trend Random fluctuations (Noise)
- 19. Autocorrelation and PartialAutocorrelation Source of image, Applied Time Series Analysis with R, Link Fig: Different forms of dependence and their Pearson’s correlation values • Correlation: Measure of linear dependence in a time series For a series Xt , • Autocorrelation: where autocovariance is defined as : • Partial autocorrelation: The coefficient of a lag in the autoregression equation:
- 20. Stationarity A time seriesis stationary if it satisfies the following conditions: • Constant mean for all t • Constant variance for all t • Autocovariance function depends only on the lag between the variables Simply put, the values of the series shouldn’t be a function of time. Why do we care? • Forecasting is easier and forecasts are more reliable • In context of autoregressive models, a necessary condition is independence of observations as they’re essentially linear regression models
- 21. Stationarity Source of images,R’s TSTutorial, Link Seasonal component Non-stationary Non-constant variance Non-stationary Constant mean, variance Stationary Can you identify whether the series is stationary? How to make the series stationary? • If series is seasonal, first seasonally difference using (R: nsdiffs), and proceed to second step; otherwise skip this step • Difference with successive data points (R: ndiffs)
- 22. Agenda • Introduction • Understandingtime series • Feature engineering and EDA • Machine learning • Tutorial on Deep Learning with TensorFlow
- 23. Data Preprocessing (R: imputeTS)(R: tsoutliers) Source of table, from left to right. 1. imputeTS, Link 2. tsoutliers, Link Type Description Additive outliers (AO) Isolated spike Level shift (LS) Abrupt change in mean level Temporary changes (TC) Spike that disappears after few periods Innovative outliers (IO) *Disturbance in innovations of model Seasonal level shifts (SLS) Abrupt seasonal change in mean level *Innovation refers to difference between observed value at time t and forecast value using information until t-1 Imputation Outlier Treatment
- 24. Feature Engineering Source ofimages, Analytics Vidhya, Link • Time-related features (such as year, month, dayofmonth, dayofweek) (Python: pd.Timestamp/pd.DatetimeIndex) • Lags of predictors (based on highest correlations given by cross-correlogram) • Rolling window (sum, min, max, weighted average over window) • Expanding window • Domain-specific features (Python: tsfresh) has a very good capability of feature engineering for time series - https://bit.ly/3odopBd Rolling Window Expanding Window
- 25. Exploratory Data Analysis Sourceof images, Top 50 Matplotlib Visualizations, Link
- 26. Agenda • Introduction • Understandingtime series • Feature engineering and EDA • Machine learning • Tutorial on Deep Learning with TensorFlow
- 27. Machine Learning Lifecycle Sourceof image, Continuous Delivery for Machine Learning, Link
- 28. Algorithms ARIMA Prophet Holt-Winters BATS,TBATS Spline Functions Theta Models STL Decomposition Neural Network Autoregression Multi-seasonal Time Series Bayesian Structural Time Series Dynamic Harmonic Regression Linear Regression LASSO Regression Ridge Regression Elastic Net Regression Random Forest Gradient Boosting Machines Adaptive Boosting Extreme Gradient Boosting Light Gradient Boosting Machines Stacking Model I Model II Model III Model IV Model V Model VI Generalized Additive Models Statistical Time Series Machine Learning Ensemble-Based (Python: NeuralProphet) Released Nov ‘20 (R: Tidymodels) Recommendation:
- 29. M-Competition Methods Method Description Naïve1 A random walk model, assuming that future values will be the same as that of the last known observation. Naïve S Forecasts are equal to the last known observation of the same period. Naïve 2 Like Naïve 1 but the data are seasonally adjusted, if needed, by applying a classical multiplicative decomposition. A 90% autocorrelation test is performed to decide whether the data are seasonal. SES Exponentially smoothing the data and extrapolating assuming no trend. Seasonal adjustments are considered as per Naïve 2. Holt Exponentially smoothing the data and extrapolating assuming a linear trend. Seasonal adjustments are considered as per Naïve 2. Damped Exponentially smoothing the data and extrapolating assuming a damped trend. Seasonal adjustments are considered as per Naïve 2. Theta As applied to the M3 Competition using two Theta lines, ϑ1=0 and ϑ2=2, with the first one being extrapolated using linear regression and the second one using SES. The forecasts are then combined using equal weights. Seasonal adjustments are considered as per Naïve 2. Comb The simple arithmetic average of SES, Holt and Damped exponential smoothing (used as the single benchmark for evaluating all other methods). • The Makridakis competitions (or M-competitions) are held for advancements in forecasting methods • The M4 competition held in 2018 had 100,000 time series at different frequencies (hourly, monthly etc.) • The data is available here Source of table, The M4 Competition: 100,000 time series and 61 forecasting methods, Link Statistical Benchmarks (Point Forecasts)
- 30. Model Evaluation throughBacktesting Source of image, Adapted from Rob J. Hyndman’s book, Link Pass 1 Pass 2 Pass 3 Pass 4 Pass 5 Pass 6 Pass 7 Pass 1 Pass 2 Pass 3 Pass 4 Pass 5 Pass 6 Pass 7 Dropped Training Forecasting Training Forecasting Sliding Window Approach Expanding Window Approach (Python: sklearn.model_selection.TimeSeriesSplit) • Backtesting allows for repeated iterations on how the model is performing and for tuning the hyperparameters • Shown below are two cross-validation mechanisms for multiple horizon forecasts (horizon is 4-steps ahead) • Forecast error expected to reduce with forecast horizon
- 31. Model Evaluation Metrics •Scale-dependent errors Mean absolute error: 𝐌𝐀𝐄 = 𝑚𝑒𝑎𝑛(|𝑒𝑡|) Root mean squared error: 𝐑𝐌𝐒𝐄 = 𝑚𝑒𝑎𝑛(𝑒𝑡 2) • Scaled errors Mean Absolute Scaled Error: 𝐌𝐀𝐒𝐄 = 𝑚𝑒𝑎𝑛(| 𝑒𝑗 1 𝑇−𝑚 𝑡=𝑚+1 𝑇 |𝑦𝑡 − 𝑦𝑡−1| |), where 𝑚 is number of seasonal periods (=1 for non-seasonal data) • Percentage errors Mean absolute percentage error: 𝐌𝐀𝐏𝐄 = 𝑚𝑒𝑎𝑛(| 100𝑒𝑡 𝑦𝑡 |) • Direction With respect to current step’s actual data, is the prediction for next step in the same direction as actual data? Source of image, Sketchplanations, Link
- 32. Model Explanation SHAP (SHapleyAdditive exPlanations) Source of images, from left to right. 1. Official Github, Link 2.Waterfall plot, Link Summary plot Waterfall plot
- 33. Model Deployment Important aspectsto consider: 1. Model refresh: • What is the minimum duration to continue with a model? • While refreshing, should same model be updated with new data? • Or is there a need to update features/algorithm? 2. Model monitoring • Data drift: How have statistical properties of model input data changed in production? • Concept drift: How have statistical properties of the target variable changed? • Model drift: Are there significant changes in the model coefficients with data refreshes? Tech stack for a Data Scientist: Containerization Model Experimentation Model Serving API API Testing
- 34. Agenda • Introduction • Understandingtime series • Feature engineering and EDA • Machine learning • Tutorial on Deep Learning with TensorFlow
- 35. Tutorial on DeepLearning in TensorFlow • Refer to Jupyter Notebook
- 36.
Editor's Notes
- #7 It all starts with data. Investment is required in data first; immature data can cause analytics to be very difficult, time consuming and less impactful
- #9 It all starts with data. Investment is required in data first; immature data can cause analytics to be very difficult, time consuming and less impactful
- #10 how well we understand the factors that contribute to it; how much data is available; whether the forecasts can affect the thing we are trying to forecast.
- #31 The same model should be more accurate for smaller horizons