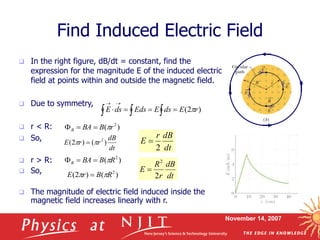
1. The document discusses Faraday's law of induction and induced electric fields. It summarizes that changing magnetic flux induces an electromotive force (emf) in a conductor. 2. Faraday's law states that the magnitude of induced emf is equal to the rate of change of magnetic flux through a conductor. A changing magnetic field also induces an electric field in space. 3. The document provides equations for calculating induced emf and electric fields. It also discusses Lenz's law, which describes the direction of induced current to oppose the change in magnetic flux that causes it.

1. Physics 121: Electricity &
Magnetism – Lecture 11
Induction I
Dale E. Gary
Wenda Cao
NJIT Physics Department

2. November 14, 2007
Currents Create Magnetic Fields
 B due to long straight wire carrying a current i:
 B due to complete loop carrying a current i :
 B inside a solenoid: a torus carrying a current i :
r
i
B


2
0

R
i
B
2
0


in
B 0

 r
iN
B
2
0




3. November 14, 2007
Induced Emf and Current
 A wire of length l is moving through a uniform
magnetic field directed into the board.
 Moving in a direction perpendicular to the field
with constant velocity v.
 Electrons feel a magnetic force and migrate,
producing an induced electric field E.
 Charges come to equilibrium when the forces on
charges balance:
 Electric field is related to potential difference
across the ends of wire:
 A potential difference is maintained between the
ends of the wire as long as the wire continues to
move through the magnetic field.




 B
v
q
FB
vB
E
qvB
qE 
 or
Blv
El
V 

 A current is set up even through no batteries are present in the circuit.
 Such a current is an induced current.
 It is produced by an induced emf.


 E
q
FE




 B
v
q
FB

4. November 14, 2007
Faraday’s Law: Experiments
 A current appears only if there is relative
motion between the loop and the magnet;
the current disappears when the relative
motion between them ceases.
 Faster motion produces a greater current.
 If moving the magnet’s north pole toward
the loop causes, say, clockwise current,
then moving the north pole away causes
counterclockwise current. Moving the
south pole toward or away from the loop
also causes currents, but in the reversed
directions.
 An emf is induced in the loop when the number of magnetic field
lines that pass through the loop is changing.

5. November 14, 2007
 We need a way to calculate the amount of
magnetic field that passes through a loop.
 Similar to the definition of electric flux, we define
a magnetic flux
 Magnetic flux is a scalar.
 In uniform magnetic field, the magnetic flux can
be expressed as
 SI unit is the weber (Wb):
1 weber = 1 Wb = 1 T m2
Flux of Magnetic Field





 dA
B
B

cos
BA
B 


6. November 14, 2007
Faraday’s Law of Induction
 The magnitude of the emf induced in a conducting loop is equal to the
rate at which the magnetic flux through that loop changes with time，
 If a coil consists of N loops with the same area,
the total induced emf in the coil is given by
 In uniform magnetic field, the induced emf can be
expressed as
 Emf can be induced in several ways,
 The magnitude of B can change with time.
 The area enclosed by the loop can change with time.
 The angle between B and the normal to the loop can change with time.
 Any combination of the above can occur.
)
cos
( 
 BA
dt
d


dt
d B




dt
d
N B





7. November 14, 2007
1. A circular loop of wire is held in a uniform magnetic field, with the
plane of the loop perpendicular to the field lines. Which of the
following will not cause a current to be induced in the loop?
A. Pushing the loop into the field.
B. Rotating the loop about an axis perpendicular to the field lines.
C. Keeping the orientation of the loop fixed and moving it along the
field lines.
D. Crushing the loop.
E. Pulling the loop out of the field.
Induced Current and Emf
B
)
cos
( 
 BA
dt
d



8. November 14, 2007
2. The graph gives the magnitude B(t) of a uniform magnetic field
that exists throughout a conducting loop, with the direction of the
field perpendicular to the plane of the loop. In which region of the
graph, the magnitude of the induced emf is the greatest?
Induced Current and Emf
B(t)
dt
t
dB
A
BA
dt
d )
(
)
cos
( 


 


9. November 14, 2007
 The change in energy in the system
must equal to the transfer of energy
into the system by work.
 Moving with constant velocity,
 Power by the applied force is
 A conducting bar of length l sliding along
two fixed parallel conducting rails.
 Free charges feel a magnetic force along the
length of the bar, producing an induced
current I.
 Start with magnetic flux
 Follow Faraday’s law, we have
 Then
 Origin of the induced current and the
energy dissipated by the resistor?
Induction and Energy Transfers
R
v
l
B
R
R
Blv
R
I
P
2
2
2
2
2









R
Blv
R
I 


Blv
dt
dx
Bl
Blx
dt
d
dt
d B




 )
(

Blx
B 

IlB
IlB
F
F B
app 

 
sin
 
R
v
l
B
v
IlB
v
F
P app
2
2
2




10. November 14, 2007
 Lenz’s law for determining the direction of an induced current in a loop.
 The induced current in a loop is in the direction that creates a magnetic
field that opposes the change in magnetic flux through the area enclosed by
the loop.
 The direction of an induced emf is that of the induced current.
 The induced current tends to keep the original magnetic flux through the
loop from changing.
Lenz’s Law
dt
d B




 Work by external agent induces current.
 Induced Bi does not always opposes B.

11. November 14, 2007
3. Which figure is physically reasonable?
Direction of induced current
N S
N
S
N S N S
N
S
v
v=0 v
v v
i i i
i i
A B C
D E
N
S
N S
N
S N
S

12. November 14, 2007
4 A circular loop of wire falling toward a wire carrying a
current to the left. What is the direction of the induced
current in the loop of wire?
A. Clockwise
B. Counterclockwise
C. Zero
D. Impossible to determine
Direction of induced current
v
I

13. November 14, 2007
 A rectangular metallic loop of dimensions l and w and resistance R moves
with constant speed v to the right. It passes through a uniform magnetic field
B directed into the page and extending a distance 3w along the x axis. Define
x as the position of the right side of the loop along the x axis.
 Plot as a function of x the magnetic flux, the induced emf, the external
applied force necessary to keep v constant.
 Definitions:
 Before entering field:
 Entering field:
 Entirely in field:
 Leaving field:
 After leaving field:
A Loop Moving Through a Magnetic Field
Blv
dt
dx
Bl
dt
d B








Blx
B 

R
v
l
B
IlB
F
F B
app
2
2



R
Blv
R
I 



14. November 14, 2007
Induced Electric Fields
 A uniform field fills a cylindrical volume of radius R.
Suppose that we increase the strength of this field at a
steady rate by increasing.
 Copper ring: A changing magnetic field produces an
electric field.
 By Faraday’s law, an induced emf and current will appear in
the ring;
 From Lenz’s law, the current flow counterclockwise;
 An induced electric field must be present along the ring;
 The existence of an electric field is independent of the
presence of any test charges. Even in the absence of the
copper ring, a changing magnetic field generates an
electric field in empty space.
 Hypothetical circle path: the electric field induced at
various points around the circle path must be tangent to
the circle.
 The electric field lines produced by the changing magnetic
field must be a set of concentric circles.
 A changing magnetic field produces an electric field.

15. November 14, 2007
A Reformulation of Faraday’s Law
 A charge q0 moving around the circular path.
 The work W done by the induced electric field,
 The work done in moving the test charge around the path,
 Two expressions for W equal to each other, we find,
 A more general expression for the work done on a charge q0
moving along any closed path,
 So,
 Combined with Faraday’s law,
 Electric potential has meaning only for electric fields produced
by static charges; it has no meaning for that by induction.

0
q
W 
rE

 2

dt
d
ds
E B







)
2
)(
( 0 r
E
q
ds
F
W 













 
 ds
E
q
ds
F
W 0




 ds
E


16. November 14, 2007
 In the right figure, dB/dt = constant, find the
expression for the magnitude E of the induced electric
field at points within and outside the magnetic field.
 Due to symmetry,
 r < R:
 So,
 r > R:
 So,
 The magnitude of electric field induced inside the
magnetic field increases linearly with r.
Find Induced Electric Field
 
 





)
2
( r
E
ds
E
Eds
ds
E 
dt
dB
r
E
2

dt
dB
r
R
E
2
2

)
( 2
r
B
BA
B 



dt
dB
r
r
E )
(
)
2
( 2

 
)
(
)
2
( 2
R
B
r
E 
 
)
( 2
R
B
BA
B 




17. November 14, 2007
Magnetic Field and Electric Field
5. The figure shows five lettered regions in which a uniform
magnetic field extends either directly out of the page or into
the page, with the direction indicated only for region a. The
field is increasing in magnitude at the same steady rate in all
five regions; the regions are identical in area. Also shown as
four numbered paths along which has the magnitudes
given below. Determine the directions of magnetic field.
A. b: c: d: e:
B. b: c: d: e:
C. b: c: d: e:
D. b: c: d: e:
E. b: c: d: e:



ds
E
Path 1 2 3 4
mag 2(mag) 3(mag) 0



ds
E

18. November 14, 2007
dt
d
ds
E B







Summary
 The magnetic flux B through an area A in a magnetic field B is defined as
 The SI unit of magnetic flux is the weber (Wb): 1Wb = 1Tm2.
 If the magnetic flux B through an area bounded by a closed conducting loop
changes with time, a current and an emf are produced in the loop; this
process is called induction. The induced emf is
 If the loop is replaced by a closely packed coil of N turns, the induced emf is
 An induced current has a direction such that the magnetic field due to the
current opposes the change in the magnetic flux that induces the current.
The induce emf has the same direction as the induce current.
 An emf is induce by a changing magnetic flux even if the loop through which
the flux is changing is not a physical conductor but an imaginary line. The
changing magnetic field induces an electric field E at every point of such a
loop; the induced emf is related to E by
where the integration is taken around the loop. We can write Faraday’s law in
its most general form,
 The essence of this law is that a changing magnetic field induces an electric
field E.





 dA
B
B
dt
d B




dt
d
N B








 ds
E
