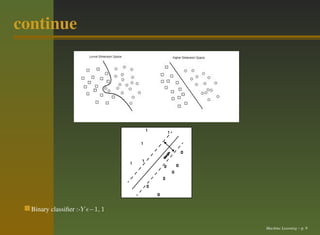
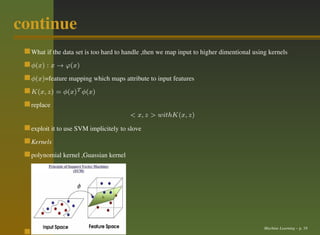
This document provides an outline for a talk on machine learning and support vector machines. It begins with an introduction to machine learning, including the goal of allowing computers to learn from examples without being explicitly programmed. It then discusses different types of machine learning problems, including supervised learning problems where labeled training data is provided. Support vector machines are introduced as a method for supervised learning classification and regression tasks by finding optimal separating hyperplanes in feature spaces. The document outlines kernels and how they can be used to map data to higher dimensions to allow for linear separation. Polynomial and Gaussian kernels are briefly described. Applications mentioned include natural language processing, data mining, speech recognition, and web classification.

1. Machine Learning
Supervised Learning and Support Vector Machine
Raj Kamal
r.kamal@iitg.ernet.in
Department of Mathematics
Indian Institute of Technology,Guwahati
Guwahati-781039,India
Machine Learning – p. 1

2. Seminar
1-1

3. Outline of the talk
Introduction
Machine Learning – p. 2

4. Outline of the talk
Introduction
Motivation
Machine Learning – p. 2

5. Outline of the talk
Introduction
Motivation
Support Vector Machines
Machine Learning – p. 2

6. Outline of the talk
Introduction
Motivation
Support Vector Machines
Softwares
Machine Learning – p. 2

7. Outline of the talk
Introduction
Motivation
Support Vector Machines
Softwares
Applications
Machine Learning – p. 2

8. Outline of the talk
Introduction
Motivation
Support Vector Machines
Softwares
Applications
Conclusion
Machine Learning – p. 2

9. Outline of the talk
Introduction
Motivation
Support Vector Machines
Softwares
Applications
Conclusion
Machine Learning – p. 2

10. Machine Learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the
design and development of algorithms that allow computers to evolve behaviors based on
empirical data, such as from sensor data or databases.
Here computer learns the algorithms from the experience.
Idea: Synthesize computer programs by learning from representative examples of input (and
output) data. Rationale Learning from Examples: A. For many problems, there is no known
method for computing the desired output from a set of inputs. B. For other problems, computation
according to the known correct method may be too expensive.
How can we build computer systems that automatically improve with experience, and what are the
fundamental laws that govern all learning processes?
Machine Learning
Machine Learning – p. 3

11. Machine Learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the
design and development of algorithms that allow computers to evolve behaviors based on
empirical data, such as from sensor data or databases.
Here computer learns the algorithms from the experience.
Idea: Synthesize computer programs by learning from representative examples of input (and
output) data. Rationale Learning from Examples: A. For many problems, there is no known
method for computing the desired output from a set of inputs. B. For other problems, computation
according to the known correct method may be too expensive.
How can we build computer systems that automatically improve with experience, and what are the
fundamental laws that govern all learning processes?
Machine Learning
Machine Learning – p. 3

12. Machine Learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the
design and development of algorithms that allow computers to evolve behaviors based on
empirical data, such as from sensor data or databases.
Here computer learns the algorithms from the experience.
Idea: Synthesize computer programs by learning from representative examples of input (and
output) data. Rationale Learning from Examples: A. For many problems, there is no known
method for computing the desired output from a set of inputs. B. For other problems, computation
according to the known correct method may be too expensive.
How can we build computer systems that automatically improve with experience, and what are the
fundamental laws that govern all learning processes?
Machine Learning
Machine Learning – p. 3

13. continue
What is the Learning Problem?
Learning = Improving with experience at some task
1. Improve over task T ,
2. with respect to performance measure P
3. based on experience E
Machine Learning – p. 4

14. continue
What is the Learning Problem?
Learning = Improving with experience at some task
1. Improve over task T ,
2. with respect to performance measure P
3. based on experience E
Machine Learning – p. 4

15. Variants of Machine Learning
1. Supervised Learning : Given a set of label training-data xi, yi , with xi be a set of samples and yi a
set of labels.
2. Unsupervised Learning : Given only a set of data xi . Learning without output values (data
exploration, e.g. clustering).
3. Query Learning : Learning where the learner can query the environment about the output
associated with a particular input.
4. Reinforcement Learning : Learning where the learner has a range of actions which it can take to
attempt to move towards states where it can expect high rewards. Cocktail Party Problem ,Sound
overlapping and verification
Problems are solved using methods of statistics: Regression,EM algorithm,MLE algorithm
Machine Learning – p. 5

16. Variants of Machine Learning
1. Supervised Learning : Given a set of label training-data xi, yi , with xi be a set of samples and yi a
set of labels.
2. Unsupervised Learning : Given only a set of data xi . Learning without output values (data
exploration, e.g. clustering).
3. Query Learning : Learning where the learner can query the environment about the output
associated with a particular input.
4. Reinforcement Learning : Learning where the learner has a range of actions which it can take to
attempt to move towards states where it can expect high rewards. Cocktail Party Problem ,Sound
overlapping and verification
Problems are solved using methods of statistics: Regression,EM algorithm,MLE algorithm
Machine Learning – p. 5

17. Variants of Machine Learning
1. Supervised Learning : Given a set of label training-data xi, yi , with xi be a set of samples and yi a
set of labels.
2. Unsupervised Learning : Given only a set of data xi . Learning without output values (data
exploration, e.g. clustering).
3. Query Learning : Learning where the learner can query the environment about the output
associated with a particular input.
4. Reinforcement Learning : Learning where the learner has a range of actions which it can take to
attempt to move towards states where it can expect high rewards. Cocktail Party Problem ,Sound
overlapping and verification
Problems are solved using methods of statistics: Regression,EM algorithm,MLE algorithm
Machine Learning – p. 5

18. Supervised Learning
1. Training Set :- Training Examples where input and output are known from experiment
2. x(i) :- ith Input value/vector
3. y (i) :- ith Output value/vector
4. (x(i) ,y (i) ) i=1...m:- Training set,m input and output training examples
5. X :- space of input value/vector
6. Y :- space of output value/vector.
7. To describe the supervised learning problem,our goal is to learn a function h(x) : X → Y . such
that h(x) is a good predictor of corresponding value of y.
8. h(x) :- hypothesis
Machine Learning – p. 6

19. Continue
1. When Target Domain is continuos we call learning problem a Regression Problem.
2. When Y can take descrete value we call it as Classification Problem
3. x ∈ ℜn ,n= no. of features
4. xi :- jth feature of ith training set.
j
5. an ith training set can have different features (shapes,size,cost).
6. To perform Supervised Learning,we must decide how we are going to do .
7. hℜθ = θ0 + θ1 ∗ x1 + ... + θn ∗ xn .
8. hθ (x) = Σθi ∗ xi where x0 = 1
9. classifier =0,1
Machine Learning – p. 7

20. Support Vector Machine(SVM)
Most classification tasks are not as simple ,more complex structure are needed to make optimal
separation,full separation would require a curve
We can see the original objects mapped i.e, rearranged using a set of mathematical functions called
kernels.By this they are linearly separable
Instead of constructing the complex curve all we have to do is to find a optimal line that can separate
these as positive and negative examples
SVM is primarily a classifier method that performs classification task by cosntructing
Goal : To optimize decision boundary.
Machine Learning – p. 8

21. continue
Binary classifier :-Y ǫ−1, 1
Machine Learning – p. 9

22. continue
Y ǫ−1, 1
hω,b (x) = g(ω T x + b)
θi are repalced with ωi
g(z) = 1, z ≥ 0
g(z) = 0, otherwise
ω = (ω1 , ω2 , ....., ωn )T
Machine Learning – p. 10

23. continue
Functional Margin:
Given (x(i) , y (i0 ) ith training set we define Functional Margin
ˆ
Υ(i) = y (i) (ω (T ) x + b)
y (i) = −1 functional margin to be large we need (ω T x + b) to be large (more negative)
y (i) = 1 functional margin to be large we need (ω T x + b) to be large (more positive)
functional margin large,so that our predictio is correct and confident.
Although it is not a good measure (scaling can have adverse effect ,it scales up just by
exploiting the scaling freedom and make functional margin large )
Functional Margin:
Υ = min(Υˆ )i = 1, 2, 3, ...m.
ˆ (i)
Machine Learning – p. 11

24. continue
Geometric Margin
decision boundary corresponding to (ω,b)
distance of A from decision boundary =AB Υ(i)
(ω)
( ω ) unit vector pointing in same direction as ω
i i ω
x −Υ ∗ →B
ω Machine Learning – p. 12

25. continue
the above satisfy ω T ∗ x + b = 0
solving :- γ (i) = ( ω
ω ∗ x(i) + b
ω )
Geometrical Margin :
(i) (i) ω b
γ =y ∗( ) ∗ x(i) +
ω ω
It is invariant to scaling.
γ = min(γ (i) ), i = 1, 2..m
Machine Learning – p. 13

26. continue
OPTIMAL MARGIN CLASSIFIER
Given a Training set,it seems from previous natural
desideration is to find decision
boundary that optimizes the geometric margin,since
this would reject a very confident set of
prediction on the training set and a good fit to train
data.
Classifier that separates positive and negative
training examples with gap.
Machine Learning – p. 14

27. continue
This lead to the following Optimization Problem
maxΥωb Υi = 1, 2, .., m
ˆ
such that y (i) ((ω)T xi + b) ≥ Υi = 1, 2, ...m
ω 2 = 1 Functional Margin = Geometric Margin
Functional margin at least Υ and we maximise Geometric margin.
ˆ
Υ
maxΥωb ω 2
such thaty (i) ((ω)T xi ˆ
+ b) ≥ Υi = 1, 2, ...m
ˆ
impose Υ = 1
minΥ,ω,b 1 ω 2
2
such that y (i) ((ω)T xi + b) ≥ 1i = 1, 2, ...m
The following gives optimal Margin Classifier ,we can solve by QP quadratic programming Code.
Machine Learning – p. 15

28. continue
gi (ω) = −y i (ω T xi + b) + 1
¸
OPtical Margin Classifiers
minΥ,ω,b 1 ω 2
2
such that gi (ω) ≤ 0
¸
Dual
maxαW (α) = Σαi − 1 Σy (i) y (j) αi αj < x(i) , x(j) > αi ≥ 0, i = 1, 2, ...m
2
Σαi y (i) = 0i = 1, 2, , ...m
Machine Learning – p. 16

29. continue
on Solving we get
ω = Σαi y (i) x(i)
max( i : y (i) = −1)ω T X (i) + min( i : y (i) = 1)ω T X (i)
b=
2
f (x) = ω T X + b = Σ( i = 1, 2, ..m)αi y (i) < xi , x > +b
hω,b (x) = g(ω T x + b)
Machine Learning – p. 17

30. continue
What if Data set is too hard to linearly separate
We add slack variables ξ to allow misclassification of difficult noise reults called Soft Margin
Primal
1
minγ,ω,b ( ω )2 + CΣm ξi
i=1
2
such that
y (i) (ω T ∗ x(i) + b) ≥ 1 − ξi i = 1, 2, ..., m
ξi ≥ 0
,i=1,2,..m
now we have permitted to chose functional margin less than 1
C[Σξi
controls Machine Learning – p. 18

31. continue
What if the data set is too hard to handle ,then we map input to higher dimentional using kernels
φ(x) : x → ϕ(x)
φ(x)=feature mapping which maps attribute to input features
K(x, z) = φ(x)T φ(x)
replace
< x, z > withK(x, z)
exploit it to use SVM implicitely to slove
Kernels
polynomial kernel ,Guassian kernel
Machine Learning – p. 19

32. continue
Polynomial kernel
 
x1 x1
 
 x1 x2 
 
 
 x1 x3 
 
 
 x2 x1 
 
 x2 x2 
 
 
x x 
 2 3 
 
φ(x) = 
 x3 x1 

 
 x3 x2 
 
 
 x3 x3 
√ 
 2cx1 
  Machine Learning – p. 20
 

33. continue
Polynomial Kernel
K(x, z) =< xT z + c >d
Guassian kernel
2
x−z
K(x, z) = exp( )
−2σ 2
Kernel helps in computation by reducing time
complexity
Machine Learning – p. 21

34. Machine Learning
1. Natural Language processing
2. Data Mining
3. Speech Recognition
4. Classifying web Documents,emails
5. Statistics
6. Economics
7. Finance
8. Robotics
9. .. and so on
Machine Learning – p. 22