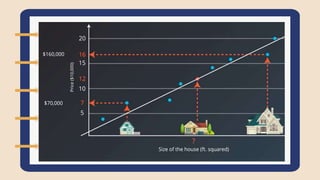
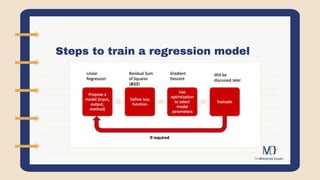
The document discusses linear regression, an algorithm used in machine learning and statistics. Linear regression is a simple and well-understood algorithm that finds a linear relationship between input variables (x) and an output variable (y). It assumes the dependence of y on x1, x2, etc. is linear. The document provides examples of using linear regression to predict house prices based on characteristics or advertising sales based on budgets. It also discusses calculating the mean squared error to evaluate a regression model's performance and the gradient descent algorithm used to minimize error and learn the model's weights.

1. Machine Learning
Algorithms
By:Mohamed Essam

2. Linear regression

3. Linear regression is perhaps one of
the most well known and well
understood algorithms in
statistics and machine learning.

4. Linear regression is perhaps one of the most
well known and well understood
algorithms in statistics and machine
learning.

5. Linear regression
Machine learning, more specifically the field of predictive
modeling is primarily concerned with minimizing the error
of a model or making the most accurate predictions
possible, at the expense of explain ability.

6. Example: advertising data

7. 2.Try to be closer for all
data

8. Linear Regression

9. 1.We Start by draw random
line throw the data.

10. 2.Try to be closer for all
data

11. 2.Try to be closer for all
data

12. Linear regression
Linear regression is a simple approach to supervised
Learning.
It assumes that the dependence of Y on x1,x2,xp is linear.

13. Linear regression
As such, linear regression was developed in the field of statistics
and is studied as a model for understanding the
relationship between input and output numerical variables,
but has been borrowed by machine learning. It is both a statistical
algorithm and a machine learning algorithm.

14. Linear regression
Linear regression is a linear model, e.g. a model that assumes a linear
relationship between the input variables (x) and the single output
variable (y). More specifically, that y can be calculated from a linear
combination of the input variables (x).
When there is a single input variable (x), the method is referred to
as simple linear regression. When there are multiple input
variables, literature from statistics often refers to the method as
multiple linear regression

15. Example
Questions we might ask:
Is there a relationship between advertising budget and sales?
How strong is the relationship between advertising budget and
sales?
Which media contribute to sales?
How accurately can we predict future sales?
Is the relationship linear?
Is there synergy among the advertising media?

16. Example
Questions we might ask:
Is there a relationship between advertising budget and sales?
How strong is the relationship between advertising budget and
sales?
Which media contribute to sales?
How accurately can we predict future sales?
Is the relationship linear?
Is there synergy among the advertising media?

17. Simple linear regression using a
single predictor X.
We assume a model
Y = β0 + β1X + ε,
where β0 and β1 are two unknown constants that represent the
intercept and slope, also known as coefficients or parameters, and ε is
the error term.
 Given some estimates βˆ0 and βˆ1 for the model coefficients, we
predict future sales using
yˆ = βˆ0 + βˆ1x,
where yˆ indicates a prediction of Y on the basis of X = x. The hat
symbol denotes an estimated value.

18. Example: advertising data

19. Example
Given a history of sold houses in the last 5 years within a
certain neighborhood, your client wants you to build a
system that can estimate the fair price of a house given its
characteristics (size, number of rooms, etc.)
• What is the output of the model?
• Is it quantitative or qualitative?
• What are the input features?
• Are these features quantitative or qualitative?

20. Let’s Assume.

21. Steps to train a regression model

22. What Is Mean Squared Error?
The Mean Squared Error measures how
close a regression line is to a set of data
points. It is a risk function corresponding
to the expected value of the squared error
loss.
Mean square error is calculated by taking
the average, specifically the mean, of
errors squared from data as it relates to a
function.

23. Mean Squared Error

24. WHY WE DO SQUARE THE
ERROR?
The squaring is necessary to remove any negative signs.
It also gives more weight to larger differences. It's called
the mean squared error as you're finding the average of a
set of errors. The lower the MSE, the better the forecast.

25. Calculate Mean Square Error
Using Excel
Now, you will learn how you can
calculate the MSE using Excel.
Suppose you have the sales data
of a product of all the months.
Step 1: Enter the actual and
forecasted data into two separate
columns.

26. Calculate Mean Square Error
Using Excel
Step 2: Calculate the squared error
of each data
The squared error is calculated by
(actual – forecast)2
MSE = (1/12) * (98) = 8.166
The MSE for this model is 8.17.

27. Gradient Descent

28. Gradient Descent
Gradient (SGD): in plain terms means slope or slant of a surface. So
gradient descent literally means descending a slope to reach the lowest
point on that surface.
 use linear regression problems to explain the gradient descent
algorithm. The objective of regression is to minimize the sum of squared
residuals. We know that a function reaches its minimum value when the
slope is equal to 0. By using this technique, we solved the linear
regression problem and learned the weight vector. The same problem can
be solved by the gradient descent technique.

29. Gradient Descent
SGD Equation:
Cost Function Equation:
𝒋𝒕𝒓𝒂𝒊𝒏 𝜽 =
𝟏
𝟐𝒎
𝒊=𝟏
𝒎
(𝒉𝜽 𝒙𝒊
− 𝒚(𝒊)
)𝟐
𝒉𝒚𝒑𝒐𝒕𝒉𝒆𝒔𝒊𝒔 𝒉𝜽 (𝒙) = 𝜽𝒋
𝒏
𝒋=𝟎
𝒙𝒋

30. Gradient Descent

31. CREDITS: This presentation template was created by Slidesgo,
including icons by Flaticon, and infographics & images by Freepik
Thank you