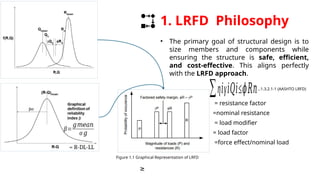
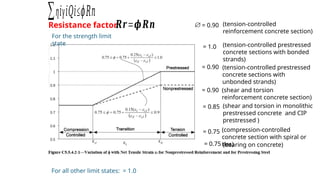
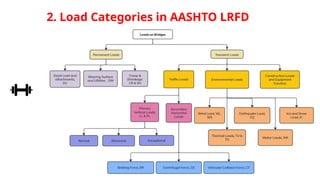
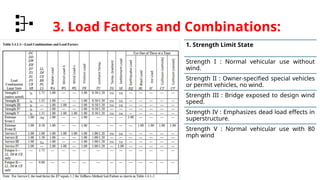
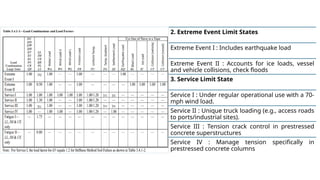
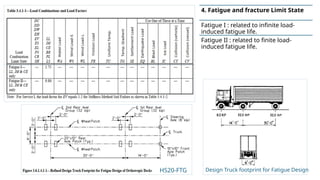
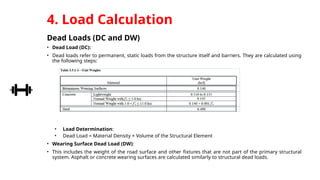
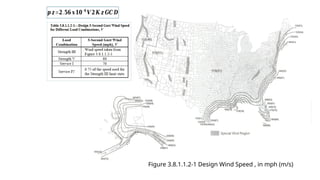
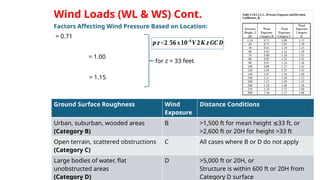
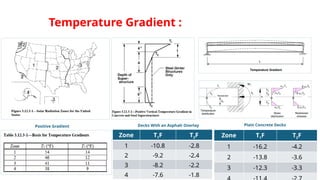
This is a genuine effort to understand load combinations as per AASHTO codes, though not all load cases are covered. An additional note: The content is for study purposes only; I do not claim ownership or authorship, as it is compiled from publicly available sources.

1. Loads &
Load Combinations to AASHTO
Presentation by
Hariyali
March 21, 2025

2. Flow of Presentation
1. Philosophy of LRFD
2. Load Categories in AASHTO LRFD
3. Load factors & Combinations
4. Load Calculation

3. Figure 1.1 Graphical Representation of LRFD
≥
1. LRFD Philosophy
• The primary goal of structural design is to
size members and components while
ensuring the structure is safe, efficient,
and cost-effective. This aligns perfectly
with the LRFD approach.
β=
𝑔𝑚𝑒𝑎𝑛
σ 𝑔
= R-DL-LL
∑η𝑖γ𝑖𝑄𝑖≤𝜙𝑅𝑛…1.3.2.1-1 (AASHTO LRFD)
= resistance factor
=nominal resistance
= load modifier
= load factor
=force effect/nominal load

4. LRFD (Load and Resistance Factor
Design)
ASD (Allowable/working Stress Design)
1. It applies safety factors directly to both
the loads and material Strengths. It
results in a design that balances both
factors for more efficient and
consistent safety levels.
1. The traditional method, which applies
safety factors only to the material
Strength, tends to be more
conservative and less optimized.
2. Provides a statistically optimized
safety margin.
2. Provides a fixed safety margin.
3. More efficient by optimizing safety 3. Often over-conservative, leading to
Figure 1.1 Graphical Representation f LRFD
Figure 1.2 Graphical Representation of ASD

5. Resistance factor𝑹𝒓=𝝓𝑹𝒏
For all other limit states: = 1.0
For the strength limit
state
∑η𝑖γ𝑖𝑄𝑖≤𝜙𝑅𝑛
∅= 0.90 (tension-controlled
reinforcement concrete section)
= 1.0 (tension-controlled prestressed
concrete sections with bonded
strands)
= 0.90 (tension-controlled prestressed
concrete sections with
unbonded strands)
(shear and torsion
reinforcement concrete section)
(shear and torsion in monolithic
prestressed concrete and CIP
prestressed )
(compression-controlled
concrete section with spiral or
ties)
= 0.90
= 0.85
= 0.75
(bearing on concrete)
= 0.75

6. 2. Load Categories in AASHTO LRFD

7. 3. Load Factors and Combinations:
1. Strength Limit State
Strength I : Normal vehicular use without
wind.
Strength II : Owner-specified special vehicles
or permit vehicles, no wind.
Strength III : Bridge exposed to design wind
speed.
Strength IV : Emphasizes dead load effects in
superstructure.
Strength V : Normal vehicular use with 80
mph wind

9. 2. Extreme Event Limit States
Extreme Event I : Includes earthquake load
Extreme Event II : Accounts for ice loads, vessel
and vehicle collisions, check floods
3. Service Limit State
Service I : Under regular operational use with a 70-
mph wind load.
Service II : Unique truck loading (e.g., access roads
to ports/industrial sites).
Service III : Tension crack control in prestressed
concrete superstructures
Service IV : Manage tension specifically in
prestressed concrete columns

10. 4. Fatigue and fracture Limit State
Fatigue I : related to infinite load-
induced fatigue life.
Fatigue II : related to finite load-
induced fatigue life.
HS20-FTG Design Truck footprint for Fatigue Design

11. 4. Load Calculation
Dead Loads (DC and DW)
• Dead Load (DC):
• Dead loads refer to permanent, static loads from the structure itself and barriers. They are calculated using
the following steps:
• Load Determination:
• Dead Load = Material Density × Volume of the Structural Element
• Wearing Surface Dead Load (DW):
• This includes the weight of the road surface and other fixtures that are not part of the primary structural
system. Asphalt or concrete wearing surfaces are calculated similarly to structural dead loads.

12. Vehicular Live Loads (LL)
• AASHTO uses a standardized truckload model called HL93 for design. This represents
a typical truck weight and configurations, including axle loads and spacing.
Design for Truck
1.Design Truck HL-93
2.Design Tandem HL-93
3.Design Lane Load
HL-93
Fig. 1.3 Permit Vehicle
(Federal Highway
Fig. 1.2 Lane and Truck
Loading Combination
3.6.1.2.2-1—Characteristics of the Design Truck (AASHTO)
Fig. 1.2 Design Lane Load
(AASHTO)
HL-93TRK
HL-93TDM
Fig. 1.1 Design Tandem
(AASHTO)

13. Number of Design Lanes
•Standard design lane width = 12.0 ft, unless specified otherwise.
•Number of design lanes = integer part of (clear roadway width / 12.0 ft).
•If traffic lanes are narrower than 12.0 ft, use actual traffic lane width, and
number of lanes equals actual number of traffic lanes.
•For roadway widths between 20 and 24 ft, always use two design lanes, each half
of the roadway width.
Multiple Presence Factor
MPF ensures a realistic assessment of bridge loads
by considering that not all lanes are likely to
experience their full design loads simultaneously
under normal traffic conditions.

14. Dynamic Load Allowance
(IM)
The impact factor accounts for the dynamic
effects of vehicles moving over the bridge.
According to AASHTO:
• 1.75 for deck joints
• 1.15 for fatigue limit states
• 1.33 for all other limit states
Centrifugal Forces
(CE)
The centrifugal effect on live load shall be
taken as the product of the axle weights of
the design truck or tandem and the factor C
where,
Centrifugal forces shall be applied
horizontally at a distance 6.0 ft above the
roadway surface.
𝐶= 𝑓 𝑥
𝑣2
𝑔𝑅 ………………………..….(3.6.3-1)

15. • A pedestrian load of 0.075 kilo-pound
per square foot shall be applied to all
sidewalks wider than 2.0 ft and
considered simultaneously with the
vehicular design live load in the
vehicle lane.
Pedestrian Loads (PL)
Braking Loads (BR)
The braking force shall be taken as the greater of:
1. 25 percent of the axle weights of the design truck or design tandem, or
2. Five percent of the design truck plus lane load or five percent of the design tandem
plus lane load
• This braking force shall be placed in all design lanes irrespective of traffic direction.
• These forces shall be assumed to act horizontally at a distance of 6.0 ft above the
roadway
• The multiple presence factors shall apply

17. Vehicular Collision Force (CT)
• To protect structures from collisions, we have two options:
1.Provide Structural Resistance, or
2.Redirect/Absorb Collision Load using Barriers.
Option 1: Structural Resistance
• If we choose to make the structure resist the collision, the pier or abutment should
be designed to resist a 600 kip static force,
This force is applied:
• Horizontally in a direction ranging from 0 to 15 degrees from the edge of
pavement,
• At a height between 2 to 5 feet above ground
Option 2: Redirect or Absorb Using Barrier
• Use a 42-inch high MASH TL-5 crash-tested rigid concrete barrier.
• Place the barrier at least 3.25 feet away from the face of the pier.

18. Water Loads (WA)
1. Static Water Pressure,
2. Buoyancy, and
3. Stream Pressure — which includes both longitudinal and lateral
components
1. Static Water Pressure
𝑝=
1
2
𝛾 𝑊 𝐻 2
2. Buoyancy
𝑝=𝛾 𝑊 𝑥 𝑉
= Unit weight of water
= height of water above base
= Unit weight of water
= Volume of submerged part of the structure

19. Water Loads (WA)
𝑝=
𝐶 𝐿𝑉 2
1000
3. Stream Pressure (Flowing Water Pressure)
a) Longitudinal stream Pressure
b) Lateral Stream Pressure
𝑝=
𝐶 𝐷𝑉 2
1000

20. Wind loads are calculated based on wind velocity, exposure category, and the area
exposed to wind.
Calculation:
WS = Wind Pressure × Exposed Area
Wind pressure on a bridge is a function of the wind speed, air density, and the area of
the structure exposed to wind.
The general equation for wind pressure acting on a surface is given by:
Where:
= Design wind pressure (ksf)
= Design 3-second gust wind speed specified (mph); (Table 3.8.1.1.2-1)
= Pressure exposure and elevation coefficient,
G = Gust effect factor, accounting for fluctuations in wind speed over time (Table
3.8.1.2.1-1)
CD = Drag coefficient (Table 3.8.1.2.1-2)
Wind Loads (WS & WL)
𝑝 𝑧=2.56 𝑥10−6
𝑉 2 𝐾 𝑧𝐺𝐶 𝐷

21. Figure 3.8.1.1.2-1 Design Wind Speed , in mph (m/s)
𝒑 𝒛=𝟐.𝟓𝟔 𝒙𝟏𝟎−𝟔
𝑽 𝟐𝑲 𝒛 𝑮𝑪 𝑫

22. 𝒑 𝒛=𝟐.𝟓𝟔 𝒙𝟏𝟎−𝟔
𝑽 𝟐𝑲 𝒛 𝑮𝑪 𝑫
Factors Affecting Wind Pressure Based on Location:
Wind Loads (WL & WS) Cont.
Ground Surface Roughness Wind
Exposure
Distance Conditions
Urban, suburban, wooded areas
(Category B)
B >1,500 ft for mean height 33 ft, or
≤
>2,600 ft or 20H for height >33 ft
Open terrain, scattered obstructions
(Category C)
C All cases where B or D do not apply
Large bodies of water, flat
unobstructed areas
(Category D)
D >5,000 ft or 20H, or
Structure is within 600 ft or 20H from
Category D surface
= 0.71
= 1.00
= 1.15
for z = 33 feet

23. 𝒑 𝒛=𝟐.𝟓𝟔 𝒙𝟏𝟎−𝟔
𝑽 𝟐𝑲 𝒛 𝑮𝑪 𝑫
Wind Loads (WL & WS) Cont.

24. Wind Load on Live Load:
For typical girder and slab bridges (span 150 ft and height 33 ft)
≤ ≤
1. Transverse component : 0.10 klf transverse
2. Longitudinal component : 0.04 klf longitudinal
Vertical Wind Pressure: Vertical wind pressure x Width of deck (including parapets and
sidewalks)
• 0.020 ksf for Strength III load combination
• 0.010 ksf for Service IV load combination
Vertical wind load is considered only for Strength III ( does not include wind on live load,
WL) and Service IV load combinations.
Wind Loads (WL & WS) Cont.

25. Thermal Load
• There are two thermal effects which potentially induce stresses in bridges, these are :
1. Uniform Temperature:
2. Gradient Temperature:
Uniform Temperature:
1. Procedure A Temperature Ranges
………………………………………………3.12.2.3-1
Coefficient of thermal expansion (e.g., 6.5×10 6
−
/F for steel)
= Length of member

26. 2. Procedure B Temperature Ranges
Determination of Design Temperatures:
For concrete girder bridges with concrete decks:
=To be obtained from Figure 3.12.2.2-1.
=To be obtained from Figure 3.12.2.2-2.
For steel girder bridges with concrete decks:
= To be obtained from Figure 3.12.2.2-3.
= To be obtained from Figure 3.12.2.2-4.

27. Temperature Gradient :
Zone T1F T2F
1 -16.2 -4.2
2 -13.8 -3.6
3 -12.3 -3.3
Decks With an Asphalt Overlay
Zone T1F T2F
1 -10.8 -2.8
2 -9.2 -2.4
3 -8.2 -2.2
4 -7.6 -1.8
Plain Concrete Decks
Positive Gradient

28. Thank You !
Any Questions…