Документ описывает оптимизации, используемые в вычислениях, особенно в 3D графике и обработке чисел с плавающей запятой. Основное внимание уделяется алгоритму быстрого вычисления обратного квадратного корня и операциям с указателями для повышения эффективности работы компилятора. Приведены примеры кода и обсуждаются различные методы оптимизации, включая устранение избыточных загрузок и хранений.

1. Alias analysis in the nutshell
Дмитрий Каш цын, HDSoftии

2. Как работает компилятор
1. Прочитать текст программы из файла
2. Записать исполняемый файл

3. 3

4. 4
Мистер Пинхед суров

5. 5
Но чайник Юта суровее

6. 6
Все дело в нормалях!

7. 7
Нормализация векторов
● Очень частая операция в 3D графике
(миллионы операций на кадр)
● Нормали используются при расчете
освещения, теней, отражений и т. п.
● С помощью черной магии вычисление может
быть существенно ускорено

8. 8
Немного алгебры
‖v‖=√v1
2
+v2
2
+v3
2
^v=
v
‖v‖
=
v
√‖v‖
2
=v⋅
1
√‖v‖
2
f (x)=
1
√ x

9. 9
Быстрый обратный корень
● Ключ к быстрому вычислению нормы
● Прямая работа с битовым представлением
● Числа с плавающей точкой в формате IEEE754

10. 10
Стандарт IEEE 754
sign exponent (8 bits) fraction (23 bits)
02331
0 0 1 1 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 = 0.15625
30 22 (bit index)
● Представление чисел с плавающей точкой
● Поддерживаются числа одинарной (32 бита)
и двойной (64 бита) точности
● Традиционный формат для современной
электроники

11. 11
Алгоритм rsqrt(X)
1.Вычислить половину X и запомнить

12. 12
Алгоритм rsqrt(X)
1.Вычислить половину X и запомнить
2.Сдвинуть X как uint32_t на 1 бит вправо

13. 13
Алгоритм rsqrt(X)
1.Вычислить половину X и запомнить
2.Сдвинуть X как uint32_t на 1 бит вправо
3.Вычесть полученное значение из магической
константы 0x5F3759DF

14. 14
Алгоритм rsqrt(X)
1.Вычислить половину X и запомнить
2.Сдвинуть X как uint32_t на 1 бит вправо
3.Вычесть полученное значение из магической
константы 0x5F3759DF ?! о_О

15. 15
Алгоритм rsqrt(X)
1.Вычислить половину X и запомнить
2.Сдвинуть X как uint32_t на 1 бит вправо
3.Вычесть полученное значение из магической
константы 0x5F3759DF ?! о_О
4.Интерпретировать разность, как первое
приближение результата в float

16. 16
Алгоритм rsqrt(X)
1.Вычислить половину X и запомнить
2.Сдвинуть X как uint32_t на 1 бит вправо
3.Вычесть полученное значение из магической
константы 0x5F3759DF ?! о_О
4.Интерпретировать разность, как первое
приближение результата в float
5.Методом Ньютона получить более точное
приближение (с помощью значения из 1.)

17. 17
Вариант реализации в Quake III
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
// evil floating point bit level hacking
i = * ( long * ) &y;
i = 0x5f3759df - ( i >> 1 ); // what the f*ck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration
return y;
}

18. 18
Готовим плацдарм
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
// evil floating point bit level hacking
i = * ( long * ) &y;
i = 0x5f3759df - ( i >> 1 ); // what the f*ck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration
return y;
}

19. 19
Вычисляем половину
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
// evil floating point bit level hacking
i = * ( long * ) &y;
i = 0x5f3759df - ( i >> 1 ); // what the f*ck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration
return y;
}

20. 20
Черная магия №1
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
// evil floating point bit level hacking
i = * ( long * ) &y;
i = 0x5f3759df - ( i >> 1 ); // what the f*ck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration
return y;
}

21. 21
Черная магия №2
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
// evil floating point bit level hacking
i = * ( long * ) &y;
i = 0x5f3759df - ( i >> 1 ); // what the f*ck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration
return y;
}

22. 22
Уточнение по Ньютону
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
// evil floating point bit level hacking
i = * ( long * ) &y;
i = 0x5f3759df - ( i >> 1 ); // what the f*ck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration
return y;
}

23. 23
Но зачем?!
● Используются простые битовые операции
● Позволяет вычислить значение в среднем
в 4 раза быстрее, чем считать в лоб на FPU
● Забавный пример хакинга
● В современных реалиях не имеет смысла

24. 24
Type Punning на примере сокетов
// Прототип функции bind()
int bind(int sockfd, struct sockaddr* my_addr, socklen_t addrlen);
// Заполняем параметры вызова
struct sockaddr_in sa = {0};
sa.sin_family = AF_INET;
sa.sin_port = htons(port);
// ...
// Делаем вызов
bind(sockfd, (struct sockaddr*) &sa, sizeof sa);

25. 25
#include <sys/socket.h>
/* This is the type we use for generic socket address arguments.
With GCC 2.7 and later, the funky union causes redeclarations or
uses with any of the listed types to be allowed without complaint.
G++ 2.7 does not support transparent unions so there we want the
old-style declaration, too. */
#if defined __cplusplus || !__GNUC_PREREQ (2, 7) || !defined __USE_GNU
# define __SOCKADDR_ARG struct sockaddr* __restrict
#else
# define __SOCKADDR_ALLTYPES
__SOCKADDR_ONETYPE (sockaddr)
__SOCKADDR_ONETYPE (sockaddr_in)
__SOCKADDR_ONETYPE (sockaddr_in6)
...
# define __SOCKADDR_ONETYPE(type) struct type* __restrict __##type##__;
typedef union {
__SOCKADDR_ALLTYPES
} __SOCKADDR_ARG __attribute__ ((__transparent_union__));
# undef __SOCKADDR_ONETYPE
#endif

26. 26
Объявления без оберток
typedef union {
struct sockaddr * __restrict __sockaddr__;
struct sockaddr_in * __restrict __sockaddr_in__;
struct sockaddr_in6 * __restrict __sockaddr_in6__;
// ...
} __SOCKADDR_ARG __attribute__ ((__transparent_union__));
extern int bind (
int __fd,
const __SOCKADDR_ARG __addr,
socklen_t __len
)
__THROW;

27. 27
Transparent union
// Объявление сложного типа
typedef union {
int *__ip;
union wait *__up;
} wait_status_ptr_t __attribute__ ((__transparent_union__));
// Прототип билиотечной функции
pid_t wait (wait_status_ptr_t);
//Вариант вызова согласно Posix
int w;
wait (&w);
//Вариант вызова согласно BSD 4.1
union wait w;
wait (&w);

28. 28
Быстрая инверсия знака
float invert(float value) {
uint32_t* const raw = (uint32_t*) &value;
*raw ^= (1 << 31); // меняем знак
return * (float*) raw;
}
sign exponent (8 bits) fraction (23 bits)
02331
0 0 1 1 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 = 0.15625
30 22 (bit index)

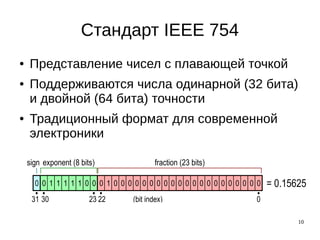
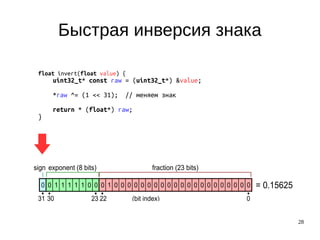
29. 29
gcc 4.4.7 -m32 -O2 -fstrict-aliasing
invert(float):
; пролог функции
push ebp
mov ebp, esp
; толкаем аргумент в стек FPU
fld dword ptr [ebp+8]
; выполняем XOR по адресу аргумента
sub dword ptr [ebp+8], 2147483648
; эпилог функции
pop ebp
ret

30. 30
-fno-strict-aliasing

31. 31
Pointer aliasing
● Возникает, когда несколько указателей
ссылаются на один участок памяти
● Анализ указателей позволяет выполнять
более агрессивные оптимизации
● Обширные возможности стрельбы по ногам

32. 32
Котики любят оптимизации!

33. 33
Основные идеи оптимизаций
● Не делать то, что никому не нужно
● Не делать дважды то, что можно сделать
один раз (а лучше не делать вообще)
● Если можно получить тот же результат, но
меньшими усилиями — это нужно сделать
● Сокращение издержек на всех уровнях

34. 34
Виды оптимизаций
● Peephole оптимизации — буквально
«через замочную скважину». Локальные
оптимизации в пределах базового блока
● Внутрипроцедурные оптимизации
● Межпроцедурные оптимизации
● Оптимизации во время линковки

35. 35
Интересующие нас оптимизации
● Redundant Load Elimination
● Redundant Store Elimination
● Common Subexpression Elimintation

36. 36
Подопытный код
int sum_array(const int* input, int* max, size_t length) {
int sum = 0;
*max = 0;
for (size_t i = 0; i < length; i++) {
*max = (input[i] > *max) ? input[i] : *max;
sum += input[i];
}
return sum;
}

37. 37
Обращения к input
int sum_array(const int* input, int* max, size_t length) {
int sum = 0;
*max = 0;
for (size_t i = 0; i < length; i++) {
*max = (input[i] > *max) ? input[i] : *max;
sum += input[i];
}
return sum;
}

38. 38
Обращения к max
int sum_array(const int* input, int* max, size_t length) {
int sum = 0;
*max = 0;
for (size_t i = 0; i < length; i++) {
*max = (input[i] > *max) ? input[i] : *max;
sum += input[i];
}
return sum;
}

39. 39
Выделение общих подвыражений
int sum_array(const int* input, int* max, size_t length) {
int sum = 0;
*max = 0;
for (size_t i = 0; i < length; i++) {
const int _max = *max;
const int _input = input[i];
*max = (_input > _max) ? _input : _max;
sum += _input;
}
return sum;
}

40. 40
Clang -m32 -O3 -mno-mmx -mno-sse
sum_array(int*, int*, int):
mov ecx, dword ptr [esp + 24] ; ecx = *length
mov edx, dword ptr [esp + 20] ; edx = max
mov dword ptr [edx], 0 ; *max = 0
xor esi, esi ; max = 0
test ecx, ecx
jle .EXIT_0 ; if (! length) return sum = 0;
mov edi, dword ptr [esp + 16] ; edi = & input[0]
xor eax, eax ; sum = 0
.LOOP_BODY:
mov ebx, dword ptr [edi] ; _input = input[i]
cmp ebx, esi ; flag = _max > _input
cmovge esi, ebx ; esi = flag ? _max : _input
mov dword ptr [edx], esi ; *max = esi
add eax, dword ptr [edi] ; sum += input[i]
add edi, 4
dec ecx
jne .LOOP_BODY
jmp .EXIT
.EXIT_0:
xor eax, eax ; sum = 0
.EXIT:
ret

41. 41
Инициализация и загрузка аргументов
sum_array(int*, int*, int):
mov ecx, dword ptr [esp + 24] ; ecx = *length
mov edx, dword ptr [esp + 20] ; edx = max
mov dword ptr [edx], 0 ; *max = 0
xor esi, esi ; max = 0
test ecx, ecx
jle .EXIT_0 ; if (! length) return sum = 0;
mov edi, dword ptr [esp + 16] ; edi = & input[0]
xor eax, eax ; sum = 0
.LOOP_BODY:
mov ebx, dword ptr [edi] ; _input = input[i]
cmp ebx, esi ; flag = _max > _input
cmovge esi, ebx ; esi = flag ? _max : _input
mov dword ptr [edx], esi ; *max = esi
add eax, dword ptr [edi] ; sum += input[i]
add edi, 4
dec ecx
jne .LOOP_BODY
jmp .EXIT
.EXIT_0:
xor eax, eax ; sum = 0
.EXIT:
ret

42. 42
Быстрая проверка на выход
sum_array(int*, int*, int):
mov ecx, dword ptr [esp + 24] ; ecx = *length
mov edx, dword ptr [esp + 20] ; edx = max
mov dword ptr [edx], 0 ; *max = 0
xor esi, esi ; max = 0
test ecx, ecx
jle .EXIT_0 ; if (! length) return sum = 0;
mov edi, dword ptr [esp + 16] ; edi = & input[0]
xor eax, eax ; sum = 0
.LOOP_BODY:
mov ebx, dword ptr [edi] ; _input = input[i]
cmp ebx, esi ; flag = _max > _input
cmovge esi, ebx ; esi = flag ? _max : _input
mov dword ptr [edx], esi ; *max = esi
add eax, dword ptr [edi] ; sum += input[i]
add edi, 4
dec ecx
jne .LOOP_BODY
jmp .EXIT
.EXIT_0:
xor eax, eax ; sum = 0
.EXIT:
ret

43. 43
Инициализация цикла по массиву
sum_array(int*, int*, int):
mov ecx, dword ptr [esp + 24] ; ecx = *length
mov edx, dword ptr [esp + 20] ; edx = max
mov dword ptr [edx], 0 ; *max = 0
xor esi, esi ; max = 0
test ecx, ecx
jle .EXIT_0 ; if (! length) return sum = 0;
mov edi, dword ptr [esp + 16] ; edi = & input[0]
xor eax, eax ; sum = 0
.LOOP_BODY:
mov ebx, dword ptr [edi] ; _input = input[i]
cmp ebx, esi ; flag = _max > _input
cmovge esi, ebx ; esi = flag ? _max : _input
mov dword ptr [edx], esi ; *max = esi
add eax, dword ptr [edi] ; sum += input[i]
add edi, 4
dec ecx
jne .LOOP_BODY
jmp .EXIT
.EXIT_0:
xor eax, eax ; sum = 0
.EXIT:
ret

44. 44
Вычисление максимума
sum_array(int*, int*, int):
mov ecx, dword ptr [esp + 24] ; ecx = *length
mov edx, dword ptr [esp + 20] ; edx = max
mov dword ptr [edx], 0 ; *max = 0
xor esi, esi ; max = 0
test ecx, ecx
jle .EXIT_0 ; if (! length) return sum = 0;
mov edi, dword ptr [esp + 16] ; edi = & input[0]
xor eax, eax ; sum = 0
.LOOP_BODY:
mov ebx, dword ptr [edi] ; _input = input[i]
cmp ebx, esi ; flag = _max > _input
cmovge esi, ebx ; esi = flag ? _max : _input
mov dword ptr [edx], esi ; *max = esi
add eax, dword ptr [edi] ; sum += input[i]
add edi, 4
dec ecx
jne .LOOP_BODY
jmp .EXIT
.EXIT_0:
xor eax, eax ; sum = 0
.EXIT:
ret

45. 45
Запись максимума и накопление суммы
sum_array(int*, int*, int):
mov ecx, dword ptr [esp + 24] ; ecx = *length
mov edx, dword ptr [esp + 20] ; edx = max
mov dword ptr [edx], 0 ; *max = 0
xor esi, esi ; max = 0
test ecx, ecx
jle .EXIT_0 ; if (! length) return sum = 0;
mov edi, dword ptr [esp + 16] ; edi = & input[0]
xor eax, eax ; sum = 0
.LOOP_BODY:
mov ebx, dword ptr [edi] ; _input = input[i]
cmp ebx, esi ; flag = _max > _input
cmovge esi, ebx ; esi = flag ? _max : _input
mov dword ptr [edx], esi ; *max = esi
add eax, dword ptr [edi] ; sum += input[i]
add edi, 4
dec ecx
jne .LOOP_BODY
jmp .EXIT
.EXIT_0:
xor eax, eax ; sum = 0
.EXIT:
ret

46. 46
Приращение переменных индукции
sum_array(int*, int*, int):
mov ecx, dword ptr [esp + 24] ; ecx = *length
mov edx, dword ptr [esp + 20] ; edx = max
mov dword ptr [edx], 0 ; *max = 0
xor esi, esi ; max = 0
test ecx, ecx
jle .EXIT_0 ; if (! length) return sum = 0;
mov edi, dword ptr [esp + 16] ; edi = & input[0]
xor eax, eax ; sum = 0
.LOOP_BODY:
mov ebx, dword ptr [edi] ; _input = input[i]
cmp ebx, esi ; flag = _max > _input
cmovge esi, ebx ; esi = flag ? _max : _input
mov dword ptr [edx], esi ; *max = esi
add eax, dword ptr [edi] ; sum += input[i]
add edi, 4
dec ecx
jne .LOOP_BODY
jmp .EXIT
.EXIT_0:
xor eax, eax ; sum = 0
.EXIT:
ret

47. 47
Проверка граничного условия на выход
sum_array(int*, int*, int):
mov ecx, dword ptr [esp + 24] ; ecx = *length
mov edx, dword ptr [esp + 20] ; edx = max
mov dword ptr [edx], 0 ; *max = 0
xor esi, esi ; max = 0
test ecx, ecx
jle .EXIT_0 ; if (! length) return sum = 0;
mov edi, dword ptr [esp + 16] ; edi = & input[0]
xor eax, eax ; sum = 0
.LOOP_BODY:
mov ebx, dword ptr [edi] ; _input = input[i]
cmp ebx, esi ; flag = _max > _input
cmovge esi, ebx ; esi = flag ? _max : _input
mov dword ptr [edx], esi ; *max = esi
add eax, dword ptr [edi] ; sum += input[i]
add edi, 4
dec ecx
jne .LOOP_BODY
jmp .EXIT
.EXIT_0:
xor eax, eax ; sum = 0
.EXIT:
ret

48. 48
Два чтения в цикле…
sum_array(int*, int*, int):
mov ecx, dword ptr [esp + 24] ; ecx = *length
mov edx, dword ptr [esp + 20] ; edx = max
mov dword ptr [edx], 0 ; *max = 0
xor esi, esi ; max = 0
test ecx, ecx
jle .EXIT_0 ; if (! length) return sum = 0;
mov edi, dword ptr [esp + 16] ; edi = & input[0]
xor eax, eax ; sum = 0
.LOOP_BODY:
mov ebx, dword ptr [edi] ; _input = input[i]
cmp ebx, esi ; flag = _max > _input
cmovge esi, ebx ; esi = flag ? _max : _input
mov dword ptr [edx], esi ; *max = esi
add eax, dword ptr [edi] ; sum += input[i]
add edi, 4
dec ecx
jne .LOOP_BODY
jmp .EXIT
.EXIT_0:
xor eax, eax ; sum = 0
.EXIT:
ret

49. 49
Но зачем?!*
* http://www.linux.org.ru/gallery/workplaces/10931314

50. 50
Пытаемся использовать ebx
sum_array(int*, int*, int):
mov ecx, dword ptr [esp + 24] ; ecx = *length
mov edx, dword ptr [esp + 20] ; edx = max
mov dword ptr [edx], 0 ; *max = 0
xor esi, esi ; max = 0
test ecx, ecx
jle .EXIT_0 ; if (! length) return sum = 0;
mov edi, dword ptr [esp + 16] ; edi = & input[0]
xor eax, eax ; sum = 0
.LOOP_BODY:
mov ebx, dword ptr [edi] ; _input = input[i]
cmp ebx, esi ; flag = _max > _input
cmovge esi, ebx ; esi = flag ? _max : _input
mov dword ptr [edx], esi ; *max = esi
— add eax, dword ptr [edi] ; sum += input[i]
+ add eax, ebx ; sum += _input
add edi, 4
dec ecx
jne .LOOP_BODY
jmp .EXIT
.EXIT_0:
xor eax, eax ; sum = 0
.EXIT:
ret

51. 51
Программы пишут человеки…
Хитрость компилятора легко компенсируется
глупостью программиста:
int fill_array(int* output, size_t length);
int sum_array(const int* input, int* max, size_t length);
void omg() {
int array[100] = {0};
fill_array(array, 100);
const int sum = sum_array(array, &array[42], 100);
return sum;
}

52. 52
Вносим max внутрь функции
int sum_array(const int* input, int* _max, size_t length) {
int sum = 0;
int max = 0;
int * const pmax = &max;
for (size_t i = 0; i < length; ++i) {
*pmax = (input[i] > *pmax) ? input[i] : *pmax;
sum += input[i];
}
*_max = *pmax; // восстанавливаем справедливость
return sum;
}

53. 53
В цикле используем pmax
int sum_array(const int* input, int* _max, size_t length) {
int sum = 0;
int max = 0;
int * const pmax = &max;
for (size_t i = 0; i < length; ++i) {
*pmax = (input[i] > *pmax) ? input[i] : *pmax;
sum += input[i];
}
*_max = *pmax; // восстанавливаем справедливость
return sum;
}

54. 54
В конце — записываем out параметр
int sum_array(const int* input, int* _max, size_t length) {
int sum = 0;
int max = 0;
int * const pmax = &max;
for (size_t i = 0; i < length; ++i) {
*pmax = (input[i] > *pmax) ? input[i] : *pmax;
sum += input[i];
}
*_max = *pmax; // восстанавливаем справедливость
return sum;
}

55. 55
Clang -m32 -O3 -mno-mmx -mno-sse
sum_array(int*, int*, int):
mov edx, dword ptr [esp + 24]
mov ecx, dword ptr [esp + 20]
xor eax, eax
test edx, edx
jle .EXIT_0
mov edi, dword ptr [esp + 16]
xor esi, esi
.LOOP_BODY:
mov ebx, dword ptr [edi]
cmp ebx, esi
cmovge esi, ebx
add eax, ebx
add edi, 4
dec edx
jne .LOOP_BODY
jmp .EXIT
.EXIT_0:
xor esi, esi
.EXIT:
mov dword ptr [ecx], esi
ret

56. 56
Нормальный человеческий цикл
sum_array(int*, int*, int):
mov edx, dword ptr [esp + 24]
mov ecx, dword ptr [esp + 20]
xor eax, eax
test edx, edx
jle .EXIT_0
mov edi, dword ptr [esp + 16]
xor esi, esi
.LOOP_BODY:
mov ebx, dword ptr [edi]
cmp ebx, esi
cmovge esi, ebx
add eax, ebx
add edi, 4
dec edx
jne .LOOP_BODY
jmp .EXIT
.EXIT_0:
xor esi, esi
.EXIT:
mov dword ptr [ecx], esi
ret

57. 57
Один раз читаем массив…
sum_array(int*, int*, int):
mov edx, dword ptr [esp + 24]
mov ecx, dword ptr [esp + 20]
xor eax, eax
test edx, edx
jle .EXIT_0
mov edi, dword ptr [esp + 16]
xor esi, esi
.LOOP_BODY:
mov ebx, dword ptr [edi]
cmp ebx, esi
cmovge esi, ebx
add eax, ebx
add edi, 4
dec edx
jne .LOOP_BODY
jmp .EXIT
.EXIT_0:
xor esi, esi
.EXIT:
mov dword ptr [ecx], esi
ret

58. 58
…и один раз записываем результат
sum_array(int*, int*, int):
mov edx, dword ptr [esp + 24]
mov ecx, dword ptr [esp + 20]
xor eax, eax
test edx, edx
jle .EXIT_0
mov edi, dword ptr [esp + 16]
xor esi, esi
.LOOP_BODY:
mov ebx, dword ptr [edi]
cmp ebx, esi
cmovge esi, ebx
add eax, ebx
add edi, 4
dec edx
jne .LOOP_BODY
jmp .EXIT
.EXIT_0:
xor esi, esi
.EXIT:
mov dword ptr [ecx], esi
ret

59. 59
Лучше не использовать out параметры
● Переменная max переехала в тело функции
● Результаты возвращаются парой
● Компилятор может оптимизировать
std::pair<int, int> sum_array(const int* input, size_t length) {
int sum = 0;
int max = 0;
for (size_t i = 0; i < length; i++) {
max = (input[i] > max) ? input[i] : max;
sum += input[i];
}
return std::make_pair(sum, max);
}

60. 60
Как все это делается?

61. 61
define i32 @sum_array(int*, int*, int)(i32* %input, i32* %_max, i32 %length) #0
{
%1 = icmp sgt i32 %length, 0
br i1 %1, label %.lr.ph, label %._crit_edge
.lr.ph: ; preds = %0, %.lr.ph
%i.03 = phi i32 [ %6, %.lr.ph ], [ 0, %0 ]
%sum.02 = phi i32 [ %5, %.lr.ph ], [ 0, %0 ]
%max.01 = phi i32 [ %.max.0, %.lr.ph ], [ 0, %0 ]
%2 = getelementptr inbounds i32, i32* %input, i32 %i.03
%3 = load i32, i32* %2, align 4
%4 = icmp sgt i32 %3, %max.01
%.max.0 = select i1 %4, i32 %3, i32 %max.01
%5 = add nsw i32 %3, %sum.02
%6 = add nuw nsw i32 %i.03, 1
%exitcond = icmp eq i32 %6, %length
br i1 %exitcond, label %._crit_edge, label %.lr.ph
._crit_edge: ; preds = %.lr.ph, %0
%sum.0.lcssa = phi i32 [ 0, %0 ], [ %5, %.lr.ph ]
%max.0.lcssa = phi i32 [ 0, %0 ], [ %.max.0, %.lr.ph ]
store i32 %max.0.lcssa, i32* %_max, align 4
ret i32 %sum.0.lcssa
}

62. 62
Вспоминаем основы RISC
● Простой фиксированный формат команды
● Простые регистровые операции
● Мухи и котлеты: работа с памятью отдельно
от операций с регистрами

63. 63
LLVM IR напоминает RISC
● Работа с памятью через load и store
● Работа с «регистрами» — SSA

64. 64
define i32 @sum_array(int*, int*, int)(i32* %input, i32* %_max, i32 %length) #0
{
%1 = icmp sgt i32 %length, 0
br i1 %1, label %.lr.ph, label %._crit_edge
.lr.ph: ; preds = %0, %.lr.ph
%i.03 = phi i32 [ %6, %.lr.ph ], [ 0, %0 ]
%sum.02 = phi i32 [ %5, %.lr.ph ], [ 0, %0 ]
%max.01 = phi i32 [ %.max.0, %.lr.ph ], [ 0, %0 ]
%2 = getelementptr inbounds i32, i32* %input, i32 %i.03
%3 = load i32, i32* %2, align 4
%4 = icmp sgt i32 %3, %max.01
%.max.0 = select i1 %4, i32 %3, i32 %max.01
%5 = add nsw i32 %3, %sum.02
%6 = add nuw nsw i32 %i.03, 1
%exitcond = icmp eq i32 %6, %length
br i1 %exitcond, label %._crit_edge, label %.lr.ph
._crit_edge: ; preds = %.lr.ph, %0
%sum.0.lcssa = phi i32 [ 0, %0 ], [ %5, %.lr.ph ]
%max.0.lcssa = phi i32 [ 0, %0 ], [ %.max.0, %.lr.ph ]
store i32 %max.0.lcssa, i32* %_max, align 4
ret i32 %sum.0.lcssa
}

65. 65
define i32 @sum_array(int*, int*, int)(i32* %input, i32* %_max, i32 %length) #0
{
%1 = icmp sgt i32 %length, 0
br i1 %1, label %.lr.ph, label %._crit_edge
.lr.ph: ; preds = %0, %.lr.ph
%i.03 = phi i32 [ %6, %.lr.ph ], [ 0, %0 ]
%sum.02 = phi i32 [ %5, %.lr.ph ], [ 0, %0 ]
%max.01 = phi i32 [ %.max.0, %.lr.ph ], [ 0, %0 ]
%2 = getelementptr inbounds i32, i32* %input, i32 %i.03
%3 = load i32, i32* %2, %.lr.ph 4
%4 = icmp sgt i32 %3, %max.01
%.max.0 = select i1 %4, i32 %3, i32 %max.01
%5 = add nsw i32 %3, %sum.02
%6 = add nuw nsw i32 %i.03, 1
%exitcond = icmp eq i32 %6, %length
br i1 %exitcond, label %._crit_edge, label %.lr.ph
._crit_edge: ; preds = %.lr.ph, %0
%sum.0.lcssa = phi i32 [ 0, %0 ], [ %5, %.lr.ph ]
%max.0.lcssa = phi i32 [ 0, %0 ], [ %.max.0, %.lr.ph ]
store i32 %max.0.lcssa, i32* %_max, %.lr.ph 4
ret i32 %sum.0.lcssa
}

66. 66
define i32 @sum_array(int*, int*, int)(i32* %input, i32* %_max, i32 %length) #0
{
%1 = icmp sgt i32 %length, 0
br i1 %1, label %.lr.ph, label %._crit_edge
.lr.ph: ; preds = %0, %.lr.ph
%i.03 = phi i32 [ %6, %.lr.ph ], [ 0, %0 ]
%sum.02 = phi i32 [ %5, %.lr.ph ], [ 0, %0 ]
%max.01 = phi i32 [ %.max.0, %.lr.ph ], [ 0, %0 ]
%2 = getelementptr inbounds i32, i32* %input, i32 %i.03
%3 = load i32, i32* %2, align 4
%4 = icmp sgt i32 %3, %max.01
%.max.0 = select i1 %4, i32 %3, i32 %max.01
%5 = add nsw i32 %3, %sum.02
%6 = add nuw nsw i32 %i.03, 1
%exitcond = icmp eq i32 %6, %length
br i1 %exitcond, label %._crit_edge, label %.lr.ph
._crit_edge: ; preds = %.lr.ph, %0
%sum.0.lcssa = phi i32 [ 0, %0 ], [ %5, %.lr.ph ]
%max.0.lcssa = phi i32 [ 0, %0 ], [ %.max.0, %.lr.ph ]
store i32 %max.0.lcssa, i32* %_max, align 4
ret i32 %sum.0.lcssa
}

67. 67
define i32 @sum_array(int*, int*, int)(i32* %input, i32* %_max, i32 %length) #0
{
%1 = icmp sgt i32 %length, 0
br i1 %1, label %.lr.ph, label %._crit_edge
.lr.ph: ; preds = %0, %.lr.ph
%i.03 = phi i32 [ %6, %.lr.ph ], [ 0, %0 ]
%sum.02 = phi i32 [ %5, %.lr.ph ], [ 0, %0 ]
%max.01 = phi i32 [ %.max.0, %.lr.ph ], [ 0, %0 ]
%2 = getelementptr inbounds i32, i32* %input, i32 %i.03
%3 = load i32, i32* %2, align 4
%4 = icmp sgt i32 %3, %max.01
%.max.0 = select i1 %4, i32 %3, i32 %max.01
%5 = add nsw i32 %3, %sum.02
%6 = add nuw nsw i32 %i.03, 1
%exitcond = icmp eq i32 %6, %length
br i1 %exitcond, label %._crit_edge, label %.lr.ph
._crit_edge: ; preds = %.lr.ph, %0
%sum.0.lcssa = phi i32 [ 0, %0 ], [ %5, %.lr.ph ]
%max.0.lcssa = phi i32 [ 0, %0 ], [ %.max.0, %.lr.ph ]
store i32 %max.0.lcssa, i32* %_max, align 4
ret i32 %sum.0.lcssa
}

68. 68
define i32 @sum_array(int*, int*, int)(i32* %input, i32* %_max, i32 %length) #0
{
%1 = icmp sgt i32 %length, 0
br i1 %1, label %.lr.ph, label %._crit_edge
.lr.ph: ; preds = %0, %.lr.ph
%i.03 = phi i32 [ %6, %.lr.ph ], [ 0, %0 ]
%sum.02 = phi i32 [ %5, %.lr.ph ], [ 0, %0 ]
%max.01 = phi i32 [ %.max.0, %.lr.ph ], [ 0, %0 ]
%2 = getelementptr inbounds i32, i32* %input, i32 %i.03
%3 = load i32, i32* %2, align 4
%4 = icmp sgt i32 %3, %max.01
%.max.0 = select i1 %4, i32 %3, i32 %max.01
%5 = add nsw i32 %3, %sum.02
%6 = add nuw nsw i32 %i.03, 1
%exitcond = icmp eq i32 %6, %length
br i1 %exitcond, label %._crit_edge, label %.lr.ph
._crit_edge: ; preds = %.lr.ph, %0
%sum.0.lcssa = phi i32 [ 0, %0 ], [ %5, %.lr.ph ]
%max.0.lcssa = phi i32 [ 0, %0 ], [ %.max.0, %.lr.ph ]
store i32 %max.0.lcssa, i32* %_max, align 4
ret i32 %sum.0.lcssa
}

69. 69
define i32 @sum_array(int*, int*, int)(i32* %input, i32* %_max, i32 %length) #0
{
%1 = icmp sgt i32 %length, 0
br i1 %1, label %.lr.ph, label %._crit_edge
.lr.ph: ; preds = %0, %.lr.ph
%i.03 = phi i32 [ %6, %.lr.ph ], [ 0, %0 ]
%sum.02 = phi i32 [ %5, %.lr.ph ], [ 0, %0 ]
%max.01 = phi i32 [ %.max.0, %.lr.ph ], [ 0, %0 ]
%2 = getelementptr inbounds i32, i32* %input, i32 %i.03
%3 = load i32, i32* %2, align 4
%4 = icmp sgt i32 %3, %max.01
%.max.0 = select i1 %4, i32 %3, i32 %max.01
%5 = add nsw i32 %3, %sum.02
%6 = add nuw nsw i32 %i.03, 1
%exitcond = icmp eq i32 %6, %length
br i1 %exitcond, label %._crit_edge, label %.lr.ph
._crit_edge: ; preds = %.lr.ph, %0
%sum.0.lcssa = phi i32 [ 0, %0 ], [ %5, %.lr.ph ]
%max.0.lcssa = phi i32 [ 0, %0 ], [ %.max.0, %.lr.ph ]
store i32 %max.0.lcssa, i32* %_max, align 4
ret i32 %sum.0.lcssa
}

70. 70
define i32 @sum_array(int*, int*, int)(i32* %input, i32* %_max, i32 %length) #0
{
%1 = icmp sgt i32 %length, 0
br i1 %1, label %.lr.ph, label %._crit_edge
.lr.ph: ; preds = %0, %.lr.ph
%i.03 = phi i32 [ %6, %.lr.ph ], [ 0, %0 ]
%sum.02 = phi i32 [ %5, %.lr.ph ], [ 0, %0 ]
%max.01 = phi i32 [ %.max.0, %.lr.ph ], [ 0, %0 ]
%2 = getelementptr inbounds i32, i32* %input, i32 %i.03
%3 = load i32, i32* %2, align 4
%4 = icmp sgt i32 %3, %max.01
%.max.0 = select i1 %4, i32 %3, i32 %max.01
%5 = add nsw i32 %3, %sum.02
%6 = add nuw nsw i32 %i.03, 1
%exitcond = icmp eq i32 %6, %length
br i1 %exitcond, label %._crit_edge, label %.lr.ph
._crit_edge: ; preds = %.lr.ph, %0
%sum.0.lcssa = phi i32 [ 0, %0 ], [ %5, %.lr.ph ]
%max.0.lcssa = phi i32 [ 0, %0 ], [ %.max.0, %.lr.ph ]
store i32 %max.0.lcssa, i32* %_max, align 4
ret i32 %sum.0.lcssa
}

71. 71
define i32 @sum_array(int*, int*, int)(i32* %input, i32* %_max, i32 %length) #0
{
%1 = icmp sgt i32 %length, 0
br i1 %1, label %.lr.ph, label %._crit_edge
.lr.ph: ; preds = %0, %.lr.ph
%i.03 = phi i32 [ %6, %.lr.ph ], [ 0, %0 ]
%sum.02 = phi i32 [ %5, %.lr.ph ], [ 0, %0 ]
%max.01 = phi i32 [ %.max.0, %.lr.ph ], [ 0, %0 ]
%2 = getelementptr inbounds i32, i32* %input, i32 %i.03
%3 = load i32, i32* %2, align 4
%4 = icmp sgt i32 %3, %max.01
%.max.0 = select i1 %4, i32 %3, i32 %max.01
%5 = add nsw i32 %3, %sum.02
%6 = add nuw nsw i32 %i.03, 1
%exitcond = icmp eq i32 %6, %length
br i1 %exitcond, label %._crit_edge, label %.lr.ph
._crit_edge: ; preds = %.lr.ph, %0
%sum.0.lcssa = phi i32 [ 0, %0 ], [ %5, %.lr.ph ]
%max.0.lcssa = phi i32 [ 0, %0 ], [ %.max.0, %.lr.ph ]
store i32 %max.0.lcssa, i32* %_max, align 4
ret i32 %sum.0.lcssa
}

72. 72
define i32 @sum_array(int*, int*, int)(i32* %input, i32* %_max, i32 %length) #0
{
%1 = icmp sgt i32 %length, 0
br i1 %1, label %.lr.ph, label %._crit_edge
.lr.ph: ; preds = %0, %.lr.ph
%i.03 = phi i32 [ %6, %.lr.ph ], [ 0, %0 ]
%sum.02 = phi i32 [ %5, %.lr.ph ], [ 0, %0 ]
%max.01 = phi i32 [ %.max.0, %.lr.ph ], [ 0, %0 ]
%2 = getelementptr inbounds i32, i32* %input, i32 %i.03
%3 = load i32, i32* %2, align 4
%4 = icmp sgt i32 %3, %max.01
%.max.0 = select i1 %4, i32 %3, i32 %max.01
%5 = add nsw i32 %3, %sum.02
%6 = add nuw nsw i32 %i.03, 1
%exitcond = icmp eq i32 %6, %length
br i1 %exitcond, label %._crit_edge, label %.lr.ph
._crit_edge: ; preds = %.lr.ph, %0
%sum.0.lcssa = phi i32 [ 0, %0 ], [ %5, %.lr.ph ]
%max.0.lcssa = phi i32 [ 0, %0 ], [ %.max.0, %.lr.ph ]
store i32 %max.0.lcssa, i32* %_max, align 4
ret i32 %sum.0.lcssa
}

73. 73
define i32 @sum_array(int*, int*, int)(i32* %input, i32* %_max, i32 %length) #0
{
%1 = icmp sgt i32 %length, 0
br i1 %1, label %.lr.ph, label %._crit_edge
.lr.ph: ; preds = %0, %.lr.ph
%i.03 = phi i32 [ %6, %.lr.ph ], [ 0, %0 ]
%sum.02 = phi i32 [ %5, %.lr.ph ], [ 0, %0 ]
%max.01 = phi i32 [ %.max.0, %.lr.ph ], [ 0, %0 ]
%2 = getelementptr inbounds i32, i32* %input, i32 %i.03
%3 = load i32, i32* %2, align 4
%4 = icmp sgt i32 %3, %max.01
%.max.0 = select i1 %4, i32 %3, i32 %max.01
%5 = add nsw i32 %3, %sum.02
%6 = add nuw nsw i32 %i.03, 1
%exitcond = icmp eq i32 %6, %length
br i1 %exitcond, label %._crit_edge, label %.lr.ph
._crit_edge: ; preds = %.lr.ph, %0
%sum.0.lcssa = phi i32 [ 0, %0 ], [ %5, %.lr.ph ]
%max.0.lcssa = phi i32 [ 0, %0 ], [ %.max.0, %.lr.ph ]
store i32 %max.0.lcssa, i32* %_max, align 4
ret i32 %sum.0.lcssa
}

74. 74
define i32 @sum_array(int*, int*, int)(i32* %input, i32* %_max, i32 %length) #0
{
%1 = icmp sgt i32 %length, 0
br i1 %1, label %.lr.ph, label %._crit_edge
.lr.ph: ; preds = %0, %.lr.ph
%i.03 = phi i32 [ %6, %.lr.ph ], [ 0, %0 ]
%sum.02 = phi i32 [ %5, %.lr.ph ], [ 0, %0 ]
%max.01 = phi i32 [ %.max.0, %.lr.ph ], [ 0, %0 ]
%2 = getelementptr inbounds i32, i32* %input, i32 %i.03
%3 = load i32, i32* %2, align 4
%4 = icmp sgt i32 %3, %max.01
%.max.0 = select i1 %4, i32 %3, i32 %max.01
%5 = add nsw i32 %3, %sum.02
%6 = add nuw nsw i32 %i.03, 1
%exitcond = icmp eq i32 %6, %length
br i1 %exitcond, label %._crit_edge, label %.lr.ph
._crit_edge: ; preds = %.lr.ph, %0
%sum.0.lcssa = phi i32 [ 0, %0 ], [ %5, %.lr.ph ]
%max.0.lcssa = phi i32 [ 0, %0 ], [ %.max.0, %.lr.ph ]
store i32 %max.0.lcssa, i32* %_max, align 4
ret i32 %sum.0.lcssa
}

75. 75
define i32 @sum_array(int*, int*, int)(i32* %input, i32* %_max, i32 %length) #0
{
%1 = icmp sgt i32 %length, 0
br i1 %1, label %.lr.ph, label %._crit_edge
.lr.ph: ; preds = %0, %.lr.ph
%i.03 = phi i32 [ %6, %.lr.ph ], [ 0, %0 ]
%sum.02 = phi i32 [ %5, %.lr.ph ], [ 0, %0 ]
%max.01 = phi i32 [ %.max.0, %.lr.ph ], [ 0, %0 ]
%2 = getelementptr inbounds i32, i32* %input, i32 %i.03
%3 = load i32, i32* %2, align 4
%4 = icmp sgt i32 %3, %max.01
%.max.0 = select i1 %4, i32 %3, i32 %max.01
%5 = add nsw i32 %3, %sum.02
%6 = add nuw nsw i32 %i.03, 1
%exitcond = icmp eq i32 %6, %length
br i1 %exitcond, label %._crit_edge, label %.lr.ph
._crit_edge: ; preds = %.lr.ph, %0
%sum.0.lcssa = phi i32 [ 0, %0 ], [ %5, %.lr.ph ]
%max.0.lcssa = phi i32 [ 0, %0 ], [ %.max.0, %.lr.ph ]
store i32 %max.0.lcssa, i32* %_max, align 4
ret i32 %sum.0.lcssa
}

76. 76
А где тут alias analysis?

77. 77
Варианты ответа анализатора
● NoAlias — никогда не пересекаются
● MustAlias — пересекаются всегда
● MayAlias — могут пересекаться

78. 78
Чему равно c?
int* a = foo();
int* b = bar();
*a = 1;
*b = 2;
int c = *a + 1;

79. 79
Эквивалентный код (MayAlias)
%a = i32* call @foo
%b = i32* call @bar
store i32 1, i32* %a
store i32 2, i32* %b
%a.2 = load i32, i32* %a, align
4
%c = add nsw i32 %a.2, 1;

80. 80
● Позволяет не накосячить с оптимизацией
потенциально зависимых значений
● Медленный, но корректный код
● Значение по умолчанию
Отношение MayAlias:

81. 81
Если указатели не пересекаются
int x;
int y;
int* a = &x;
int* b = &y;
*a = 1;
*b = 2;
int c = *a + 1;

82. 82
Эквивалентный код (NoAlias)
%a = alloca i32, align 4
%b = alloca i32, align 4
store i32 1, i32* %a
store i32 2, i32* %b
%a.2 = load i32, i32* %a, align
4
%c = add nsw i32 %a.2, 1;

83. 83
Проталкиваем константу
Удаляем лишнее чтение
%a = alloca i32, align 4
%b = alloca i32, align 4
store i32 1, i32* %a
store i32 2, i32* %b
%a.2 = load i32, i32* %a, align
4
%c = add nsw 1, 1;

84. 84
Упрощаем выражение
%a = alloca i32, align 4
%b = alloca i32, align 4
store i32 1, i32* %a
store i32 2, i32* %b
%a.2 = load i32, i32* %a, align
4
%c = add nsw 1, 1
%c = 2

85. 85
NoAlias позволяет:
● Удалить лишние операции с памятью
● Выполнять перестановку операций
● Выполнять оптимизации над независимыми
значениями, без оглядки друг на друга
● Результат — более эффективный код

86. 86
Если указатели пересекаются
int x;
int* a = &x;
int* b = &x;
*a = 1;
*b = 2;
int c = *a + 1;

87. 87
Эквивалентный код (MustAlias)
%a = alloca i32, align 4
%b = i32* %a ; GEP, bitcast, ...
store i32 1, i32* %a
store i32 2, i32* %b
%a.2 = load i32, i32* %a, align
4
%c = add nsw i32 %a.2, 1;

88. 88
Удаляем лишнюю запись
%a = alloca i32, align 4
%b = i32* %a ; GEP, bitcast, ...
store i32 1, i32* %a
store i32 2, i32* %b
%a.2 = load i32, i32* %a, align
4
%c = add nsw i32 %a.2, 1;

89. 89
Проталкиваем константу
Удаляем лишнее чтение
%a = alloca i32, align 4
%b = i32* %a ; GEP, bitcast, ...
store i32 1, i32* %a
store i32 2, i32* %b
%a.2 = load i32, i32* %a, align
4
%c = add nsw 2, 1;

90. 90
Упрощаем выражение
%a = alloca i32, align 4
%b = i32* %a ; GEP, bitcast, ...
store i32 1, i32* %a
store i32 2, i32* %b
%a.2 = load i32, i32* %a, align
4
%c = add nsw 2, 1
%c = 3

91. 91
MustAlias позволяет:
● Доказать связь отдельных операций
● Выполнять оптимизации с учетом истории
● Результат — более эффективный код

92. 92
Strict aliasing и TBAA
● Cпособ уменьшить MayAlias
в пользу NoAlias и MustAlias
● Работает на базе системы типов языка
и другой «внешней» для LLVM информации
● Позволяет проводить оптимизации там,
где информация о контексте недостаточна

93. 93
Подход С
float invert(float value) {
uint32_t* const raw = (uint32_t*) &value;
*raw ^= (1 << 31); // меняем знак
return * (float*) raw;
}

94. 94
Strict aliasing vs Здравый смысл
float invert(float value) {
uint32_t* const raw = (uint32_t*) &value;
*raw ^= (1 << 31); // меняем знак
return * (float*) raw;
}
TBAA(value, raw) = TBAA(float, uint32_t) = NoAlias

95. 95
Подход Fortran
● Аргументы функций всегда независимы (кроме target)
● Тем не менее, не мешает выстрелить в ногу
● Программист ожидает «2, 4, 4». В реальности будет «2, 2, 2»
...
I = 1
CALL FOO(I, I)
PRINT *, I
END
SUBROUTINE FOO(J, K)
J = J + K
K = J * K
PRINT *, J, K
END

96. 96
Подход Java
● Язык запрещает опасную работу с указателями (почти)
● Escape analysis позволяет размещать объекты на стеке
public String getHello() {
Vector v = new Vector();
v.add("Hello");
v.add("from");
v.add("Java!");
return v.toString();
}

97. 97
Подход Rust
● Иммутабельность по умолчанию
● Концепция заимствования ссылок
● Алгебраические типы данных и сопоставление
по образцу
● Обобщенный код, типажи
● Выделенные unsafe блоки
● Контроль на этапе компиляции
● Отсутствие состояния гонок,
потокобезопасность кода гарантируется
● Абстракции нулевой стоимости

98. 98
Пример программы на Rust
fn test(vec: &Vec<i32>) -> (i32, i32) {
let mut sum: i32 = 0;
let mut max: i32 = vec[1];
for i in vec {
sum = sum + i;
max = if i > &max { *i } else { max };
}
(sum, max)
}
fn main() {
let vec = vec![1, 2, 3];
let (sum, max) = test(&vec);
println!("The sum is {}, max is {}", sum, max);
}

99. 99
Что можно почитать
● blog.llvm.org
● llvm.org/docs
● isocpp.org/std/the-standard
● doc.rust-lang.org
● halt.habrahabr.ru/topics/
● llst.org

100. Спасибо за внимание!