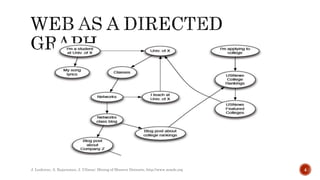
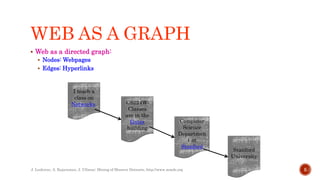
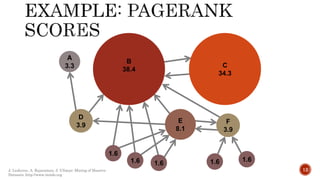
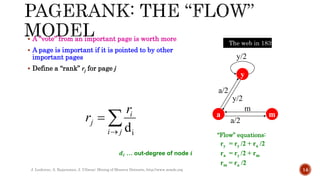
Link analysis uses graph theory to represent relationships between objects as edges in a graph. It can be used for both directed and undirected data mining. Link analysis ranking algorithms start with a set of web pages and rank them based on their link structure, with more important pages having more inbound links. PageRank is a specific link analysis algorithm that models the web as a directed graph and calculates page ranks through an iterative process where each page's rank is the sum of the ranks of pages that link to it.

1. LINK ANALYSIS
Ahnaf Tahmeed
ID:23542605015

2. LINK ANALYSIS
 Link analysis is based on a branch of mathematics called graph
theory, which represents relationships between different objects as
edges in a graph. Link analysis is not a specific modeling technique,
so it can be used for both directed and undirected data mining.
 A link analysis ranking algorithm starts with a set of Web pages.
Depending on how this set of pages is obtained, we distinguish
between query independent algorithms, and query dependent
algorithms. In the former case, the algorithm ranks the whole Web.

3. Link analysis is used for 3
primary purposes:
Find matches in data for known
patterns of interest;
Find anomalies where known
patterns are violated;
Discover new patterns of
interest (social network analysis,
data mining).

4. J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 4

5. WEB AS A GRAPH
 Web as a directed graph:
 Nodes: Webpages
 Edges: Hyperlinks
J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 5
I teach a
class on
Networks. CS224W:
Classes
are in the
Gates
building
Computer
Science
Departmen
t at
Stanford
Stanford
University

6.  First try: Human curated
Web directories
 Yahoo, DMOZ, LookSmart
 Second try: Web Search
 Information Retrieval investigates:
Find relevant docs in a small
and trusted set
 Newspaper articles, Patents, etc.
 But: Web is huge, full of untrusted
documents, random things, web spam,
etc.
J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 6

7. 2 challenges of web search:
 (1) Web contains many sources of information
Who to “trust”?
 Trick: Trustworthy pages may point to each other!
 (2) What is the “best” answer to query “newspaper”?
 No single right answer
 Trick: Pages that actually know about newspapers might all
be pointing to many newspapers
J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 7

8. RANKING NODES ON THE
GRAPH
 All web pages are not equally “important”
www.joe-schmoe.com vs. www.stanford.edu
 There is large diversity
in the web-graph
node connectivity.
Let’s rank the pages by
the link structure!
J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 8

9. Link Analysis approaches for computing
importances
of nodes in a graph:
Page Rank Algorithm
Hyperlink Induced Topic Search (HITS)
Topic-Specific (Personalized) Page Rank
Web Spam Detection Algorithms
J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 9

10. PageRank (PR) is an algorithm used by Google Search to
rank websites in their search engine results. PageRank
was named after Larry Page, one of the founders of
Google. PageRank is a way of measuring the importance of
website pages.
PageRank of a website is very important because it is the
deciding factor which shows up your site in the first page
or last page of the search engine when a browser is
searching for something related to your business or
product.

11. LINKS AS VOTES
 Idea: Links as votes
 Page is more important if it has more links
 In-coming links? Out-going links?
 Think of in-links as votes:
 www.stanford.edu has 23,400 in-links
 www.joe-schmoe.com has 1 in-link
 Are all in-links are equal?
 Links from important pages count more
 Recursive question!
J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 11

12. J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive
Datasets, http://www.mmds.org
12
B
38.4
C
34.3
E
8.1
F
3.9
D
3.9
A
3.3
1.6
1.6 1.6 1.6 1.6

13. SIMPLE RECURSIVE
FORMULATION
 Each link’s vote is proportional to the
importance of its source page
 If page j with importance rj has n out-
links, each link gets rj / n votes
 Page j’s own importance is the sum of the
votes on its in-links
J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive
Datasets, http://www.mmds.org
13
j
k
i
rj/3
rj/3
rj/3
rj = ri/3+rk/4
ri/3 rk/4

14.  A “vote” from an important page is worth more
 A page is important if it is pointed to by other
important pages
 Define a “rank” rj for page j
J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 14



j
i
i
j
r
r
i
d
y
m
a
a/2
y/2
a/2
m
y/2
The web in 1839
“Flow” equations:
ry = ry /2 + ra /2
ra = ry /2 + rm
rm = ra /2
𝒅𝒊 … out-degree of node 𝒊

15. SOLVING THE FLOW
EQUATIONS
 3 equations, 3 unknowns,
no constants
 No unique solution
 All solutions equivalent modulo the scale factor
 Additional constraint forces uniqueness:
 𝒓𝒚 + 𝒓𝒂 + 𝒓𝒎 = 𝟏
 Solution: 𝒓𝒚 =
𝟐
𝟓
, 𝒓𝒂 =
𝟐
𝟓
, 𝒓𝒎 =
𝟏
𝟓
 Gaussian elimination method works for
small examples, but we need a better method for large web-size graphs
 We need a new formulation!
J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 15
ry = ry /2 + ra /2
ra = ry /2 + rm
rm = ra /2
Flow equations:

16. PAGERANK: MATRIX
FORMULATION
 Stochastic adjacency matrix 𝑴
 Let page 𝑖 has 𝑑𝑖 out-links
 If 𝑖 → 𝑗, then 𝑀𝑗𝑖 =
1
𝑑𝑖
else 𝑀𝑗𝑖 = 0
 𝑴 is a column stochastic matrix
 Columns sum to 1
 Rank vector 𝒓: vector with an entry per page
 𝑟𝑖 is the importance score of page 𝑖
 𝑖 𝑟𝑖 = 1
 The flow equations can be written
𝒓 = 𝑴 ⋅ 𝒓
J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 16



j
i
i
j
r
r
i
d

17.  Remember the flow equation:
 Flow equation in the matrix form
𝑴 ⋅ 𝒓 = 𝒓
 Suppose page i links to 3 pages, including j
J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 17
j
i
M r r
=
rj
1/3



j
i
i
j
r
r
i
d
ri
.
. =

18. EXAMPLE: FLOW
EQUATIONS & M
J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 18
r = M∙r
y ½ ½ 0 y
a = ½ 0 1 a
m 0 ½ 0 m
y
a m
y a m
y ½ ½ 0
a ½ 0 1
m 0 ½ 0
ry = ry /2 + ra /2
ra = ry /2 + rm
rm = ra /2