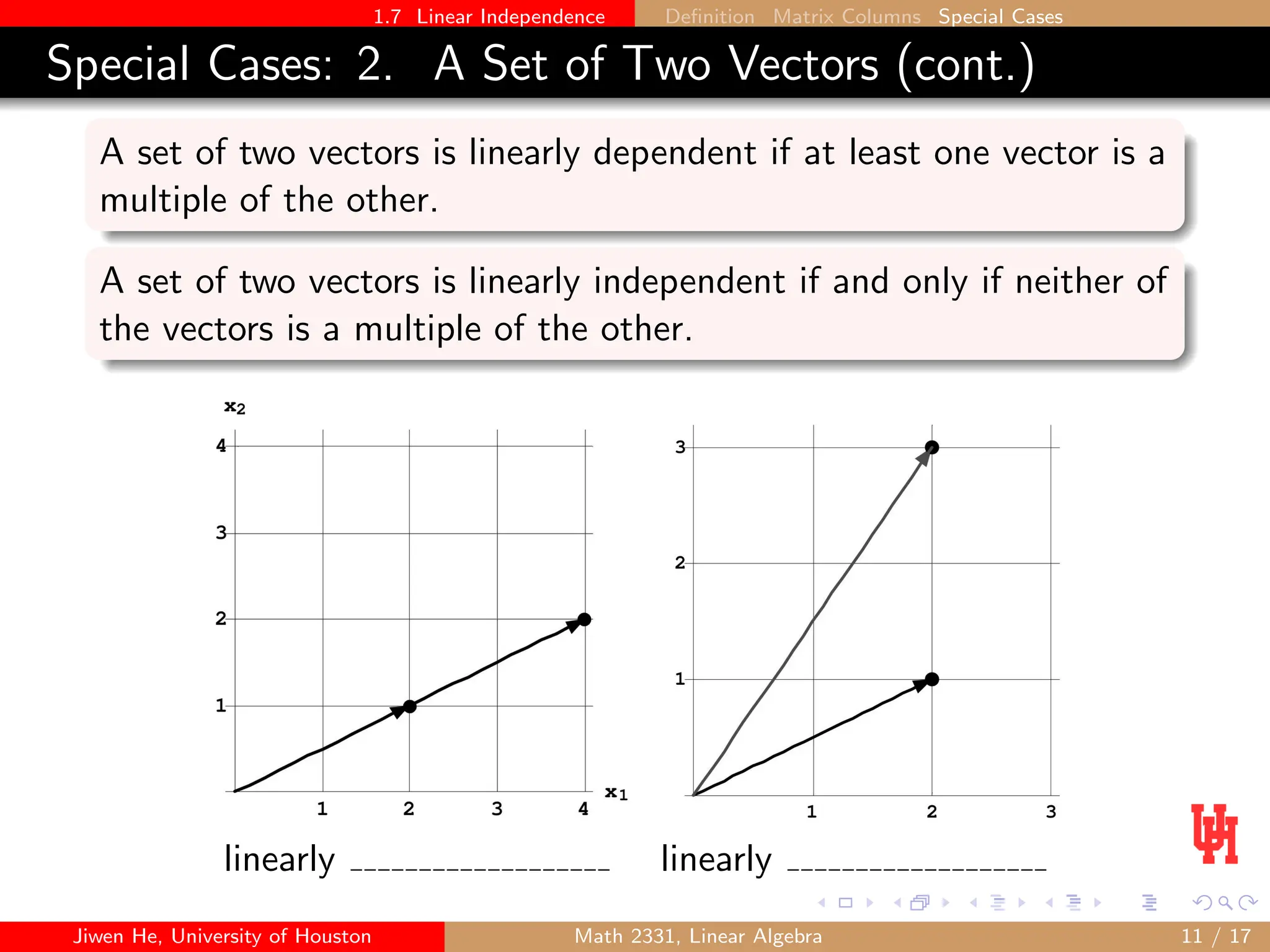
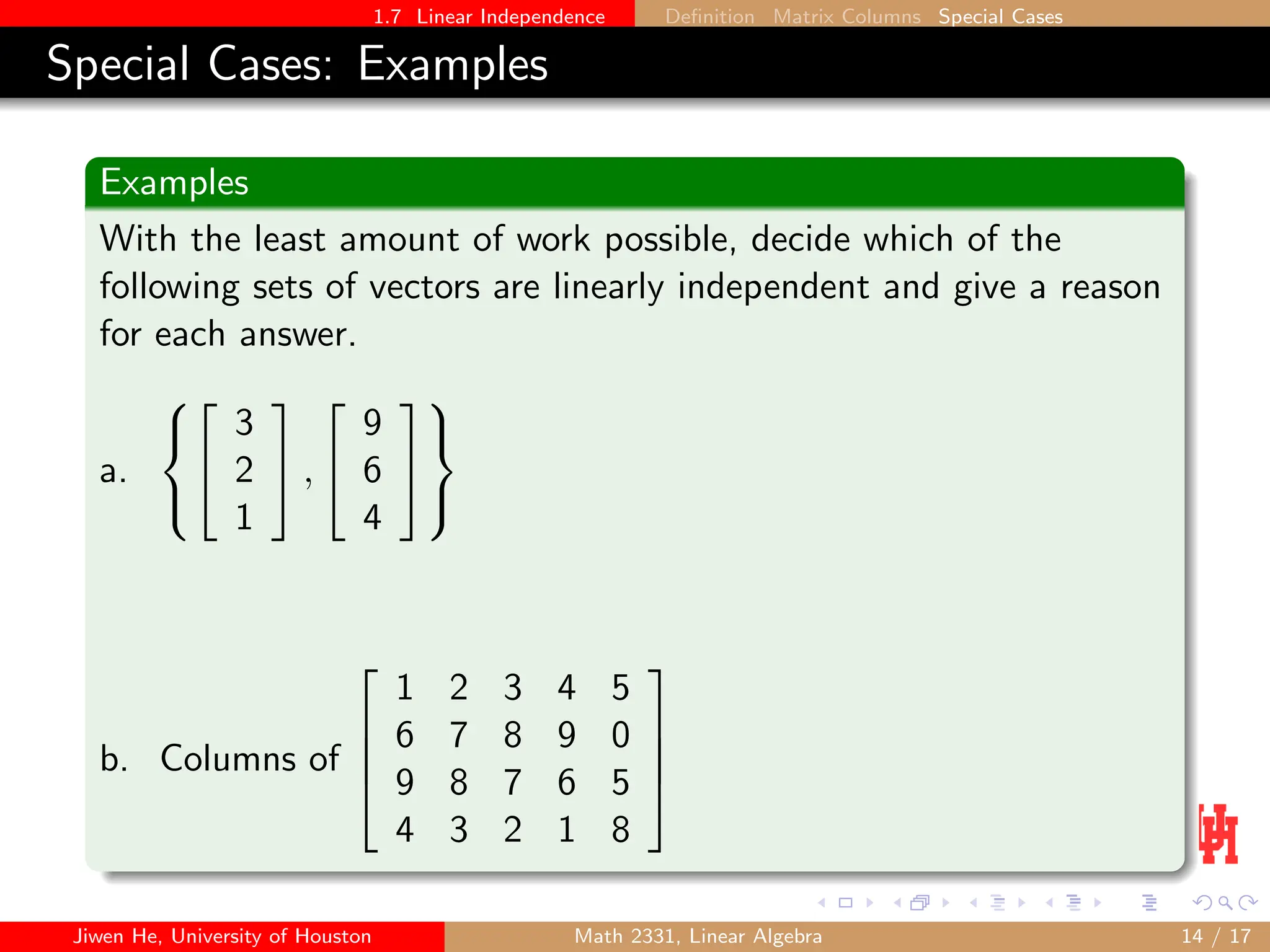
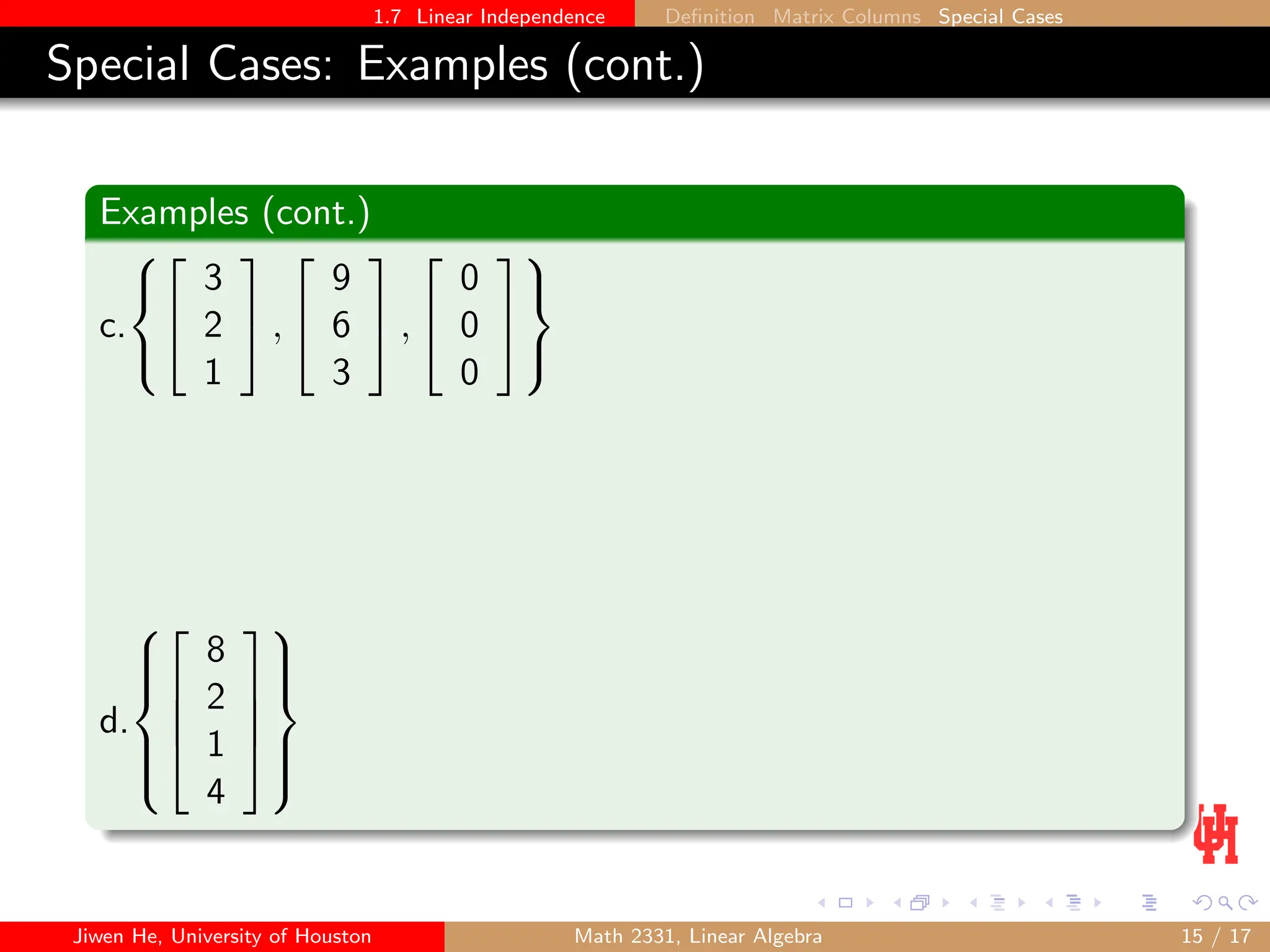
This document discusses the concept of linear independence in linear algebra, defining it in relation to vector sets and their solutions. It explains scenarios of linear dependence and independence through examples, theorems, and matrix representations. The document emphasizes that a set is linearly dependent if it contains too many vectors or the zero vector, and provides methods for determining the independence of given vector sets.