LA question Pool

Linear Algebra (LA)– Question Pool

Welcome to Success Formula Question Pool
Disclaimers
• All slides and its materials are the property of Success Formula
• You get an exclusive free personal access once buying the course the slides are made for
• The slides are individually marked, and Success Formula can track to which users they belong
• No part of this slide deck may be reproduced, distributed, or transmitted (hereafter in this slide
referred together as “Shared”) in any form or by any means, including sharing the material on
platforms such as StudyDrive
• In case slides are shared, Success Formula can attempt legal actions towards the sharing party in line
with European and Dutch Law (Copyright laws)
1
Error Bounty
• If you find any mistake in this slide deck, let us know and we will refund you the cost of the slides
• Only the first person indicating the mistake gets the refund

Answers
Question
Some people seem to like Breaking Bad, others like Prison Break. What is the percentage of people that
watch TV?
2
A. The Walking Dead
B. Depends on the year
C. All of them
D. Answer D because it is the best answer
Answer: C
Introduction question Question topic
The question
Difficulty
Answers
Correct
Answer

Matrix Multiplication and Addition
3

Answers
Question
Exam Time!
Add the following 2 matrices together, if possible:
𝐴 =
7 8 2
1 0 3
5 −4 2
𝐵 =
2 3
0 −4
1 2
4
A matrix can only be added (/subtracted) from another matrix if both have the same dimensions.
→ Not possible

Answers
Question
Exam Time!
Add the following 2 matrices together, if possible:
𝐴 =
1 −5
4 3
𝐵 =
−2 1
−4 1
5
1 −5
4 3
+
−2 1
−4 1
=
1 + (−2) −5 + 1
4 + (−4) 3 + 1
=
−1 −4
0 4

Answers
Question
Exam Time!
Multiply the following to matrices together, if possible:
𝐴 =
1 3 2
1 1 4
0 2 2
𝐵 =
2 2
1 7
1 2
6
𝐴 0 𝐵 = 𝐴𝐵
𝑚×𝑛 0 𝑛×𝑝 = 𝑚×𝑝
→ For matrix multiplication, the number of columns in the matrix must equal the number of rows in
the second. The order of the product of the matrices are the remaining unused dimensions.

Exam Time! (Continuation)
Answer
Multiply the elements of each row of the first matrix by each column of the second, and add the
products, as seen below:
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
0
𝑗 𝑘 𝑙
𝑚 𝑛 𝑜
𝑝 𝑞 𝑟
=
(𝑎𝑗 + 𝑏𝑚 + 𝑐𝑝) (𝑎𝑘 + 𝑏𝑛 + 𝑐𝑞) (𝑎𝑙 + 𝑏𝑜 + 𝑐𝑟)
(𝑑𝑗 + 𝑒𝑚 + 𝑓𝑝) (𝑑𝑘 + 𝑒𝑛 + 𝑓𝑞) (𝑑𝑙 + 𝑒𝑜 + 𝑓𝑟)
(𝑔𝑗 + ℎ𝑚 + 𝑖𝑝) (𝑔𝑘 + ℎ𝑛 + 𝑖𝑞) (𝑔𝑙 + ℎ𝑜 + 𝑖𝑟)
7
Answer
1 3 2
1 1 4
0 2 2
0
2 2
1 7
1 2
=
(1) 2 + (3) 1 + (2) 1 (1) 2 + (3) 7 + (2) 2
(1) 2 + (1) 1 + (4) 1 (1) 2 + (1) 7 + (4) 2
(0) 2 + (2) 1 + (2) 1 (0) 2 + (2) 7 + (2) 2
=
7 27
7 17
4 18

Answers
Question
Exam Time!
Multiply the following to matrices together, if possible:
𝐴 =
1 3 2
1 1 4
0 2 2
𝐵 =
1 4 7
2 7 9
−3 0 5
5 4 −4
8
𝐴 0 𝐵 = 𝐴𝐵
𝑚×𝑛 0 𝑛×𝑝 = 𝑚×𝑝
→ For matrix multiplication, the number of columns in the matrix must equal the number of rows in
the second. The order of the product of the matrices are the remaining unused dimensions.
→ In this case, matrix multiplication is not possible: 3×3 0 4×3

System of Linear Equations
9

Answers
Question
Exam Time!
Solve the following linear system using a matrix:
E
3𝑥1 + 8𝑥2 + 2𝑥3 = −5
4𝑥1 + 10𝑥2 − 6𝑥3 = 0
−𝑥1 − 2𝑥2 + 2𝑥3 = 1
10
There are 5 main steps to solving a linear system:
1) Write down the augmented matrix
2) Use the row reduction algorithm to obtain an equivalent augmented matrix in echelon form. Decide
whether the system is consistent. If there is no solution, stop; otherwise, go to the next step
3) Continue row reduction to obtain the reduced echelon form
4) Write the system of equations corresponding to the matrix obtained in step 3
5) Rewrite each nonzero equation from step 4 so that its one basic variable is expressed in terms of any
free variables appearing in the equation

Answer
E
3𝑥1 + 8𝑥2 + 2𝑥3 = −5
4𝑥1 + 10𝑥2 − 6𝑥3 = 0
−𝑥1 − 2𝑥2 + 2𝑥3 = 1
→
3 8 2
4 10 −6
−1 −2 2
0
𝑥1
𝑥2
𝑥3
=
−5
0
1
→
3 8 2 −5
4 10 −6 0
−1 −2 2 1
11
Answer
3 8 2 −5
4 10 −6 0
−1 −2 2 1
𝑅1 ↔ 𝑅3 ~
1 2 −2 −1
4 10 −6 0
3 8 2 −5
~ 𝑅2: 𝑅2 − 4𝑅1 ~
1 2 −2 −1
0 2 2 4
3 8 2 −5

Answer
1 2 −2 −1
0 2 2 4
3 8 2 −5
𝑅3: 𝑅3 − 3𝑅1 𝑅2:
1
2
𝑅2 ~
1 2 −2 −1
0 1 1 2
0 2 8 −2
𝑅3: 𝑅3 − 2𝑅1 ~
1 2 −2 −1
0 1 1 2
0 0 6 −6
12
Answer
1 2 −2 −1
0 1 1 2
0 0 6 −6
𝑅3:
1
6
𝑅3 ~
1 2 −2 −1
0 1 1 2
0 0 1 −1
𝑅2: 𝑅2 − 𝑅1 ~
1 2 −2 −1
0 1 0 3
0 0 1 −1

Answer
1 2 −2 −1
0 1 0 3
0 0 1 −1
𝑅1: 𝑅1 + 2𝑅3 ~
1 2 0 −3
0 1 0 3
0 0 1 −1
𝑅1: 𝑅1 − 2𝑅2 ~
1 0 0 −9
0 1 0 3
0 0 1 −1
13
Answer
𝑥 =
𝑥!
𝑥"
𝑥#
=
−9
3
−1

Answers
Question
Exam Time!
E
2𝑥1 + 2𝑥2 + 6𝑥3 = 0
𝑥1 + 3𝑥2 + 5𝑥3 = 0
2𝑥1 + 0𝑥2 + 4𝑥3 = 1
14

Answer
E
2𝑥1 + 2𝑥2 + 6𝑥3 = 0
𝑥1 + 3𝑥2 + 5𝑥3 = 0
2𝑥1 + 0𝑥2 + 4𝑥3 = 1
→
2 2 6
1 3 5
2 0 4
0
𝑥1
𝑥2
𝑥3
=
0
0
1
→
2 2 6 0
1 3 5 0
2 0 4 1
15
Answer
2 2 6 0
1 3 5 0
2 0 4 1
𝑅1 ↔ 𝑅2 ~
1 3 5 0
2 2 6 0
2 0 4 1
𝑅2: 𝑅2 − 2𝑅1 ~
1 3 5 0
0 −4 −4 0
2 0 4 1

Answer
1 3 5 0
0 −4 −4 0
2 0 4 1
𝑅3: 𝑅3 − 2𝑅1 ~
1 3 5 0
0 −4 −4 0
0 −6 −6 1
𝑅2: −
1
4
𝑅2 ~
1 3 5 0
0 1 1 0
0 −6 −6 1
16
Answer
1 3 5 0
0 1 1 0
0 −6 −6 1
𝑅3: 𝑅3 + 6𝑅1 ~
1 3 5 0
0 1 1 0
0 0 0 1
0 ≠ 1 ∴ 𝐼𝑛𝑐𝑜𝑛𝑠𝑖𝑠𝑡𝑒𝑛𝑡 𝑆𝑦𝑠𝑡𝑒𝑚 (𝑁𝑜 𝑆𝑜𝑙𝑢𝑡𝑖𝑜𝑛)

Answers
Question
Exam Time!
E
1𝑥1 − 2𝑥2 + 3𝑥3 = 1
2𝑥1 + 2𝑥2 − 6𝑥3 = 14
3𝑥1 − 4𝑥2 + 5𝑥3 = 7
17

Answer
E
1𝑥1 − 2𝑥2 + 3𝑥3 = 1
2𝑥1 + 2𝑥2 − 6𝑥3 = 14
3𝑥1 − 4𝑥2 + 5𝑥3 = 7
→
1 −2 3
2 2 −6
3 −4 5
0
𝑥1
𝑥2
𝑥3
=
1
14
7
→
1 −2 3 1
2 2 −6 14
3 −4 5 7
18
Answer
1 −2 3 1
2 2 −6 14
3 −4 5 7
𝑅2: 𝑅2 − 2𝑅1 ~
1 −2 3 1
0 6 −12 12
3 −4 5 7
𝑅2:
1
6
𝑅2 ~
1 −2 3 1
0 1 −2 2
3 −4 5 7

Answer
1 −2 3 1
0 1 −2 2
3 −4 5 7
𝑅3: 𝑅3 − 3𝑅1 ~
1 −2 3 1
0 1 −2 2
0 2 −4 4
𝑅3: 𝑅3 − 2𝑅2 ~
1 −2 3 1
0 1 −2 2
0 0 0 0
19
Answer
1 −2 3 1
0 1 −2 2
0 0 0 0
𝑅1: 𝑅1 + 2𝑅2 ~
1 0 −1 5
0 1 −2 2
0 0 0 0

Answer
1 0 −1 5
0 1 −2 2
0 0 0 0
0 = 0 ∴ 𝐶𝑜𝑛𝑠𝑖𝑠𝑡𝑒𝑛𝑡 𝑆𝑦𝑠𝑡𝑒𝑚 (𝐼𝑛𝑓𝑖𝑛𝑖𝑡𝑒𝑙𝑦 𝑀𝑎𝑛𝑦 𝑆𝑜𝑙𝑢𝑡𝑖𝑜𝑛𝑠, 𝑥# 𝑖𝑠 𝑓𝑟𝑒𝑒)
20
Answer
x =
𝑥!
𝑥"
𝑥#
=
5 + 𝑥#
2 + 2𝑥#
𝑓𝑟𝑒𝑒
x =
5
2
0
+ 𝑥#
1
2
1

Linear Dependency
21

Answers
Question
Exam Time!
Determine whether the following 3 vectors are linearly independent:
4
2
1
,
−8
6
5
,
2
0
0
22
A set of vectors is linearly independent if the only linear combination of the vectors equaling 0 is the
trivial one (all the coefficients are 0). In other words, the set of vectors 𝑣! … 𝑣$ are independent if:
𝐶!𝑣! + 𝐶"𝑣" + ⋯ + 𝐶$𝑣$ = 0
Has only the trivial solution 𝐶! = 𝐶" = 𝐶# = 0
Hence, you must form an augmented matrix and check the existence of free (non-basic) variables. If
none exist, the set of vectors are said to be linearly Independent.

Answer
23
Answer
4 −8 2 0
2 6 0 0
1 5 0 0
𝑅1 ↔ 𝑅3 ~
1 5 0 0
2 6 0 0
4 −8 2 0
𝑅2: 𝑅2 − 2𝑅1 𝑅3: 𝑅3 − 4𝑅1 ~
~
1 5 0 0
0 −4 0 0
0 −28 2 0
𝑅2: −
1
4
𝑅2 ~
1 5 0 0
0 1 0 0
0 −28 2 0
𝑅1: 𝑅1 − 5𝑅2 𝑅3: 𝑅3 + 28𝑅2 ~
1 0 0 0
0 1 0 0
0 0 2 0
𝑅3:
1
2
𝑅3 ~
1 0 0 0
0 1 0 0
0 0 1 0
→ All variables are basic (pivot exists in every column) → only solution is trivial solution
∴ set of vectors are independent

Answers
Question
Exam Time!
Determine whether the following 3 vectors are linearly independent:
4
2
1
,
−8
6
5
,
−4
8
6
24
A set of vectors is linearly independent if the only linear combination of the vectors equaling 0 is the
trivial one (all the coefficients are 0). In other words, the set of vectors 𝑣! … 𝑣$ are independent if:
𝐶!𝑣! + 𝐶"𝑣" + ⋯ + 𝐶$𝑣$ = 0
Has only the trivial solution 𝐶! = 𝐶" = 𝐶# = 0
Hence, you must form an augmented matrix and check the existence of free (non-basic) variables. If
none exist, the set of vectors are said to be linearly Independent.

Answer
25
Answer
4 −8 −4 0
2 6 8 0
1 5 6 0
𝑅1 ↔ 𝑅3 ~
1 5 6 0
2 6 8 0
4 −8 −4 0
𝑅2: 𝑅2 − 2𝑅1 𝑅3: 𝑅3 − 4𝑅1 ~
1 5 6 0
0 −4 −4 0
0 −28 −28 0
𝑅2: −
1
4
𝑅2 𝑅3: −
1
28
𝑅3 ~
1 5 6 0
0 1 1 0
0 1 1 0
𝑅3: 𝑅3 − 𝑅2 ~
1 5 6 0
0 1 1 0
0 0 0 0
𝑅1: 𝑅1 − 5𝑅2 ~
1 0 1 0
0 1 1 0
0 0 0 0
→ Not all variables are basic (no pivot in the third column corresponding to 𝐶#) → non-trivial solution
exists, 𝐶# is free
∴ set of vectors are dependent

Answers
Question
Exam Time!
Determine whether the following set of vectors are linearly independent:
1
3
0
,
−4
3
1
,
5
3
2
,
4
−3
−1
26
A set of vectors is also dependent when:
1. It contains the zero vector
2. At least one of the vectors is a linear combination of the other vectors
3. The set contains more vectors than vector entries (n > m in a 𝑚×𝑛 matrix)
∴ set of vectors are dependent → 4 vectors but only 3 entries

Answers
Question
Exam Time!
Determine if the following matrix is dependent or independent
A =
1 2 3
1 −3 12
4 8 12
27
A matrix is independent when the matrix equation 𝐴𝑥 = 0 only has the trivial solution and dependent
when it has nontrivial solutions.
A trivial solution is one where all the variables in 𝑥!𝑎! + 𝑥"𝑎"+ … +𝑥$𝑎$= 0 are equal to 0. Hence, you
only have one exact solution.
To find out if a matrix is independent, row reduce to get the Echelon Form.
No free variables → only trivial solution → matrix is independent
Free Variables → there are non-trivial solutions → matrix is dependent

Answer
28
Answer
1 2 3 0
1 −3 12 0
4 8 12 0
𝑅3: 𝑅3 − 4𝑅1 ~
1 2 3 0
1 −3 12 0
0 0 0 0
𝑅2: 𝑅2 − 𝑅1 ~
1 2 3 0
0 −5 9 0
0 0 0 0
One free variable (only 2 pivot columns) so there are nontrivial solutions
∴ A is dependent

Answers
Question
Exam Time!
Determine if the following matrix is dependent or independent
A =
0 3 2
1 −2 5
−1 2 4
29
A matrix is independent when the matrix equation 𝐴𝑥 = 0 only has the trivial solution and dependent
when it has nontrivial solutions.
A trivial solution is one where all the variables in 𝑥!𝑎! + 𝑥"𝑎"+ … +𝑥$𝑎$= 0 are equal to 0. Hence, you
only have one exact solution.
To find out if a matrix is independent, row reduce to get the Echelon Form.
No free variables → only trivial solution → matrix is independent
Free Variables → there are non-trivial solutions → matrix is dependent

Answer
30
Answer
0 3 2 0
1 −2 5 0
−1 2 4 0
𝑅1 ↔ 𝑅2 ~
1 −2 5 0
0 3 2 0
−1 2 4 0
𝑅3: 𝑅3 + 𝑅1 ~
1 −2 5 0
0 3 2 0
0 0 9 0
No free variables (3 pivot columns) so there is only the trivial solution
∴ A is independent

Determinants
31

Answers
Question
Exam Time!
Find the determinant of the following matrix A:
A =
8 6
3 4
32
𝐴 = 8 0 4 − 6 0 3 = 32 − 18 = 14
Explanation: The determinant of a 2x2 matrix can be calculated as the following:
𝐴 =
𝑎 𝑏
𝑐 𝑑
= 𝑎𝑑 − 𝑏𝑐

Answers
Question
Exam Time!
A =
2 0
1 1
33
𝐴 = 2 0 1 − 1 0 0 = 2 − 0 = 2
Explanation: The determinant of a 2x2 matrix can be calculated as the following:
𝐴 =
𝑎 𝑏
𝑐 𝑑
= 𝑎𝑑 − 𝑏𝑐

Answers
Question
Exam Time!
A =
1 2 3
3 2 1
1 2 3
34
𝐴 = 1 0
2 1
2 3
− 2 0
3 1
1 3
+ 3 0
3 2
1 2
= 1 2 0 3 − 2 0 1 − 2 3 0 3 − 1 0 1 + 3 3 0 2 − 1 0 2
𝐴 = 1 4 − 2 8 + 3 4 = 4 − 16 − 12 = 0
Explanation: The determinant of a nxn matrix can be calculated by expanding along the 𝑖%& row, by
cofactor expansion:
𝐴 = ∑'(!
$
𝑎)'𝐶)' = 𝑎)!𝐶)! + 𝑎)"𝐶)" + ⋯ + 𝑎)$𝐶)$
N.b: The same process can be used on any row, or even any column, from i = 1 to n.

Answers
Question
Exam Time!
A =
1 2 3
0 1 1
0 2 3
35
𝐴 = 1 0
1 1
2 3
− 0 0
2 3
2 3
+ 0 0
2 3
1 1
= 1 1 0 3 − 2 0 1 − 0 + 0 = 1
Notice how we expanded down the first column, to make the most out of the zeros in the matrix.
Explanation: The determinant of a nxn matrix can be calculated by expanding along the 𝑖%& row, by
cofactor expansion:
𝐴 = ∑'(!
$
𝑎)'𝐶)' = 𝑎)!𝐶)! + 𝑎)"𝐶)" + ⋯ + 𝑎)$𝐶)$
N.b: The same process can be used on any row, or even any column, from i = 1 to n.

Answers
Question
Exam Time!
A =
3 6 2
0 −3 6
0 0 1
36
𝐴 = 3 0 −3 0 1 = −9
Explanation:
The determinant of a triangular (upper or lower) matrix is the product of the entries on the diagonal.

Answers
Question
Exam Time!
Consider the following matrix:
𝐴 =
0 −5 7 2
3 2 1 −2
0 −1 5 3
Calculate the determinant or explain why it is not possible.
37
𝐴 is not possible, as A is not nxn (square)

Answers
Question
Exam Time!
Consider the following matrix:
𝐴 =
1 6 1
0 0 −2
0 0 3
Calculate the determinant or explain why it is not possible.
38
𝐴 = 1 0 0 0 3 = 0
Explanation:
The determinant of a triangular (upper or lower) matrix is the product of the entries on the diagonal.

Answers
Question
Exam Time!
Consider the following matrices:
𝐴 =
1 2
3 4
, 𝐵 =
4 5
9 2
0 −2
Calculate the determinant of AB or explain why it is not possible.
39
𝐴𝐵 is not possible, as A is 2x2 and B is 3x2, so they cannot be multiplied by each other.

Invertible Matrix Theorem
40

Answers
Question
Exam Time!
Find the inverse of the following matrix:
𝐴 =
5 2
−7 −3
41
For a 2×2 matrix 𝐴, the inverse 𝐴*! is:
𝑎 𝑏
𝑐 𝑑
*!
=
1
𝑎𝑑 − 𝑏𝑐
𝑑 −𝑏
−𝑐 𝑎
Determinant
Use the following fact to check your answer: 𝐴 0 𝐴*! = 𝐼

Answer
𝐴 = 𝑑𝑒𝑡𝐴 = 𝑑𝑒𝑡
5 2
−7 −3
= 5 −3 − 2 −7 = −1
𝐴*! =
1
−1
−3 −2
7 5
=
3 2
−7 −5
42
Answer
Check:
𝐴 0 𝐴*! =
5 2
−7 −3
3 2
−7 −5
=
5 3 + (2)(−7) 5 2 + (2)(−5)
−7 3 + −3 (−7) −7 2 + (−3)(−5)
=
1 0
0 1

Answers
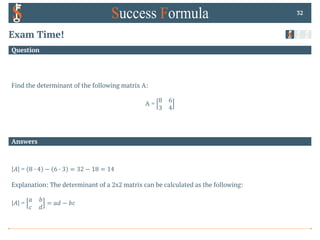
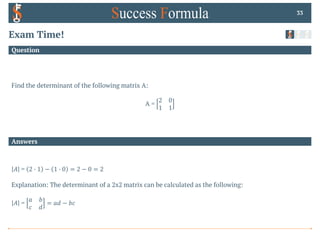
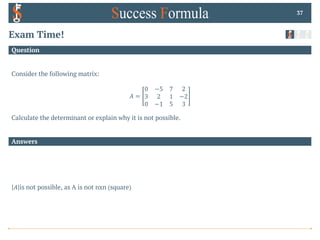
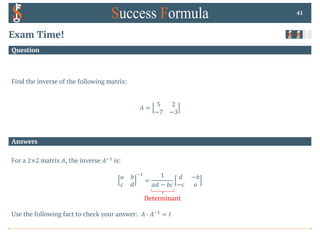
Question
Exam Time!
Find the inverse of the following matrix:
𝐴 =
1 2 2
1 2 −1
−1 1 4
43
To obtain the inverse of a 𝑛×𝑛 matrix, the equation
[A I] = [I A-1]
Needs to be solved by using row reduction.

Answer
1 2 2 1 0 0
1 2 −1 0 1 0
−1 1 4 0 0 1
𝑅2: 𝑅2 − 𝑅1 (𝑅3: 𝑅3 + 𝑅1) ~
1 2 2 1 0 0
0 0 −3 −1 1 0
0 3 6 1 0 1
𝑅2 ↔ 𝑅3 ~
1 2 2 1 0 0
0 3 6 1 0 1
0 0 −3 −1 1 0
𝑅3 = −
1
3
𝑅3 ~
1 2 2 1 0 0
0 3 6 1 0 1
0 0 1
1
3
−
1
3
0
𝑅2: 𝑅2 − 6𝑅3 ~
44
Answer
1 2 2 1 0 0
0 3 0 −1 2 1
0 0 1
1
3
−
1
3
0
𝑅1: 𝑅1 − 2𝑅3 ~
1 2 0
1
3
2
3
0
0 3 0 −1 2 1
0 0 1
1
3
−
1
3
0
𝑅2:
1
3
𝑅2 ~

Answer
1 2 0
1
3
2
3
0
0 1 0 −
1
3
2
3
1
3
0 0 1
1
3
−
1
3
0
𝑅1: 𝑅1 − 2𝑅2 ~
1 0 0 1 −
2
3
−
2
3
0 1 0 −
1
3
2
3
1
3
0 0 1
1
3
−
1
3
0
45
Answer
𝐴*! =
1 −
2
3
−
2
3
−
1
3
2
3
1
3
1
3
−
1
3
0
𝐶ℎ𝑒𝑐𝑘: 𝐴 0 𝐴*! =
1 0 0
0 1 0
0 0 1

Answers
Question
Exam Time!
46
𝑑𝑒𝑡𝐴 = 𝐴 = 1 0 0 0 −23 = 0 ∴ 𝐴 𝑖𝑠 𝑛𝑜𝑡 𝑖𝑛𝑣𝑒𝑟𝑡𝑖𝑏𝑙𝑒
Rule: A square matrix A is invertible if and only if 𝑑𝑒𝑡𝐴 ≠ 0
Determine whether the following matrix is invertible:
𝐴 =
1 0 0
3 0 0
5 4 −23

Answers
Question
Exam Time!
By using the Invertible Matrix Theorem, determine whether the following matrix is invertible:
𝐴 =
1 2 3
2 4 6
5 4 −3
47
1 2 3
2 4 6
5 4 −3
𝑅2: 𝑅2 − 2𝑅1 ~
1 2 3
0 0 0
5 4 −3
𝑅2 ↔ 𝑅3 ~
1 2 3
5 4 −3
0 0 0
𝑅2: 𝑅2 − 5𝑅1 ~
1 2 3
0 −6 −18
0 0 0
Rows 1 and 2 are scalar multiples of each other. This tells us that the matrix does not have 3 pivot (=
first non-zero entry in each row) positions → not invertible.
Also, the determinant of A = 0 → not invertible.
Rule: A 𝑛×𝑛 square matrix is invertible if it has n pivot positions.
Rule: A 𝑛×𝑛 square matrix is invertible if the determinant is non-zero.

Null, Column, and Row Space
48

Answers
Question
Exam Time!
Consider the matrix:
𝐴 =
3 1 −1
−1 1 1
Is the vector
1
−1
2
in the null space of A?
49
The null space (Null A) is the set of all linear combinations of the homogeneous equation Ax = 0 and is
a subspace of ℝ$.
Therefore, you must compute Ax and check if it satisfies Ax=0.
3 1 −1
−1 1 1
0
1
−1
2
=
3 1 + 1 −1 + (−1)(2)
−1 1 + 1 −1 + (1)(2)
=
0
0
∴ x is in Null A.

Answers
Question
Exam Time!
Consider the matrix:
𝐴 =
2 5 1
−1 −7 −5
3 4 −2
Is the vector
−2
5
1
in the col space of A?
50
The column space (Col A) is the set of all linear combinations of the columns of A for Ax = b and is a
subspace of ℝ+.
Therefore, you must form an augmented matrix with the vector as b and row reduce to check if the
solution is consistent.

Answer
2 5 1 −2
−1 −7 −5 5
3 4 −2 1
𝑅1 ↔ 𝑅2 𝑅1: −1𝑅1 ~
1 7 5 −5
2 5 1 −2
3 4 −2 1
𝑅2: 𝑅2 − 2𝑅1 𝑅3: 𝑅3 − 3𝑅1 ~
1 7 5 −5
0 −9 −9 8
0 −17 −17 16
R2: −17R2 R3 = 9R3 ~
1 7 5 −5
0 153 153 −136
0 −153 −153 144
𝑅3: 𝑅3 + 𝑅2 ~
51
Answer
1 7 5 −5
0 153 153 −136
0 0 0 8
𝑅3:
1
8
𝑅3 𝑅2:
1
153
𝑅2 ~
1 7 5 −5
0 1 1 −
8
9
0 0 0 1
𝑅1: 𝑅1 + 5𝑅3 𝑅2: 𝑅2 +
8
9
𝑅3 ~
1 7 5 0
0 1 1 0
0 0 0 1
𝑅1: 𝑅1 − 7𝑅2 ~
1 0 −2 0
0 1 1 0
0 0 0 1
Last row is inconsistent as 0 ≠ 1 ∴ the vector is not in Col A

Answers
Question
Exam Time!
Find the dimension of the null space and column space of the following matrix:
𝐴 =
1 −2 6
1 3 3
−2 4 −12
52
The dimension of the null space is the number of free variables in the equation 𝐴𝑥 = 0.
The dimension of the column space (rank) is the number of pivot columns.
𝑅𝑎𝑛𝑘 𝐴 + 𝐷𝑖𝑚 𝑁𝑢𝑙𝑙 𝐴 = 𝑛
Hence, we must transform the matrix [A 0] into Echelon Form and check how many pivots exist.

Answer
1 −2 6 0
1 3 3 0
−2 4 −12 0
𝑅3: 𝑅3 + 2𝑅1 ~
1 −2 6 0
1 3 3 0
0 0 0 0
𝑅2: 𝑅2 − 𝑅1 ~
1 −2 6 0
0 5 −3 0
0 0 0 0
53
Answer
There exists 2 pivot positions, as seen above.
Hence, dim Null A = 1 and dim Col A = 2
Notice how 1 + 2 = 3 = number of columns, n.

Answers
Question
Exam Time!
Find the basis for the null space of the following matrix:
𝐴 =
1 2 0 3
2 4 2 −4
2 4 1 1
Additionally, mention the nullity of A.
54
The dimension of the null space (=nullity) is the number of free variables in the equation 𝐴𝑥 = 0.
The null space (Null A) is the set of all linear combinations of the homogeneous equation Ax = 0 and is
a subspace of ℝ$.
Therefore, you must put the matrix in row-reduced Echelon Form. The basis is formed by writing the
solution in terms of free variables. Keep in mind, for the basis for the null space, the original matrix is
not used in providing the final answer, as it is for finding the basis for the column space (see next
question).

Answer
1 2 0 3
2 4 2 −4
2 4 1 1
𝑅2: 𝑅2 − 2𝑅1 𝑅3: 𝑅3 − 2𝑅1 ~
1 2 0 3
0 0 2 −10
0 0 1 −5
𝑅3: 𝑅3 −
1
2
𝑅2 ~
1 2 0 3
0 0 2 −10
0 0 0 0
𝑅2:
1
2
𝑅2 ~
1 2 0 3
0 0 1 −5
0 0 0 0
→ 𝑥 =
𝑥!
𝑥"
𝑥#
𝑥,
=
−2𝑥" − 3𝑥,
𝑓𝑟𝑒𝑒
5𝑥,
𝑓𝑟𝑒𝑒
Notice there are 2 pivot positions, hence 2 free variables.
55
Answer
𝑥 = 𝑥"
−2
1
0
0
+ 𝑥,
−3
0
5
1
→ 𝐵𝑎𝑠𝑖𝑠 𝑁𝑢𝑙𝑙 𝐴 =
−2
1
0
0
,
−3
0
5
1
Accordingly, the nullity is equal to 2, as there are 2 free variables.
Notice the rank is 2, and 2 + 2 = 4 (=number of columns)

Answers
Question
Exam Time!
Find the basis for the column space and row space of the following matrix:
𝐴 =
1 1 0 2
2 2 1 2
1 1 1 0
Also, find Rank A.
56
The column space (Col A) is the set of all linear combinations of the columns of A for Ax = b and is a
subspace of ℝ+.
Therefore, you must put the matrix in Echelon Form. The basis is formed by selecting the
corresponding pivot columns of A. Keep in mind, pivot columns are only evident when the matrix is in
echelon form, but the basis for Col A are from the original matrix.
The row space (Row A) is the set of all linear combinations of the row vectors and can also be written as
the transpose of the column space of A. Accordingly, in Echelon Form, the nonzero rows of the matrix
form a basis for the row space of the matrix (using rows from the reduced matrix).

Answer
1 1 0 2
2 2 1 2
1 1 1 0
R2: R2 − 2R1 R3: R3 − R1 ~
1 1 0 2
0 0 1 −2
0 0 1 −2
𝑅3: 𝑅3 − 𝑅2 ~
1 1 0 2
0 0 1 −2
0 0 0 0
57
Answer
Evidently, there are 2 pivots (in columns 1 and 3 / in rows 1 and 2). Hence:
𝐵𝑎𝑠𝑖𝑠 𝐶𝑜𝑙 𝐴 =
1
2
1
,
0
1
1
𝐵𝑎𝑠𝑖𝑠 𝑅𝑜𝑤 𝐴 =
1
1
0
2
,
0
0
1
−2

Summary
58
Null Space
• Only found in the row-reduced Echelon Form
• Dim Null A (nullity) is the amount of free variables
• Basis is formed from writing the general solution
Column Space
• Can be found from Echelon Form
• Dim Col A (= rank A) is the amount of pivot columns
• Basis is formed from the columns of the original matrix
Row Space
• Can be found from Echelon Form
• Dim Row A (= dim Col A = rank A) is the amount of pivot rows
• Basis is formed from the rows of the row reduced matrix

Eigenvalues and Eigenvectors
59

Answers
Question
Exam Time!
Determine if u and v are eigenvectors of A:
𝐴 =
2 0
3 −4
, 𝑢 =
2
1
, 𝑣 =
2
2
60
Eigenvector = A nonzero vector x that holds the equation Ax = λx, for some scalar λ. Hence, we must
compute Au and Av:
𝐴𝑢 =
2 0
3 −4
0
2
1
=
2 2 + 0 1
3 2 + −4 1
=
4
2
= 2 0
2
1
∴ 𝑢 𝑖𝑠 𝑎𝑛 𝑒𝑖𝑔𝑒𝑛𝑣𝑒𝑐𝑡𝑜𝑟 𝑤𝑖𝑡ℎ 𝑡ℎ𝑒 𝑒𝑖𝑔𝑒𝑛𝑣𝑎𝑙𝑢𝑒 = 2
𝐴𝑣 =
2 0
3 −4
0
2
2
=
2 2 + 0 2
3 2 + −4 2
=
4
−2
→ 𝑐𝑎𝑛𝑛𝑜𝑡 𝑏𝑒 𝑤𝑟𝑖𝑡𝑒𝑛 𝑖𝑛 𝑡ℎ𝑒 𝑓𝑜𝑟𝑚 λ𝑣
∴ 𝑣 𝑖𝑠 𝑛𝑜𝑡 𝑎𝑛 𝑒𝑖𝑔𝑒𝑛𝑣𝑒𝑐𝑡𝑜𝑟

Answers
Question
Exam Time!
Is 3 an eigenvalue of the following matrix? If so, find the corresponding basis for the eigenspace.
𝐴 =
5 −1 6
2 2 6
2 −1 9
61
Eigenvalue = a scalar λ where there is a nontrivial solution for Ax = λx. In other words, (A- λI)x = 0 has a
nontrivial solution. Hence, we must compute (A- λI)x = 0, row reduce it, and check if there are free
variables (nontrivital solutions):
𝐴 − λI =
5 −1 6
2 2 6
2 −1 9
− 3
1 0 0
0 1 0
0 0 1
=
5 −1 6
2 2 6
2 −1 9
−
3 0 0
0 3 0
0 0 3
=
2 −1 6
2 −1 6
2 −1 6

Answer
2 −1 6 0
2 −1 6 0
2 −1 6 0
𝑅2: 𝑅2 − 𝑅1 𝑅3: 𝑅3 − 𝑅1 ~
2 −1 6 0
0 0 0 0
0 0 0 0
𝑅1:
1
2
𝑅1 ~
1 −
1
2
3 0
0 0 0 0
0 0 0 0
62
Answer
1 − a
1
2 3 0
0 0 0 0
0 0 0 0
∴ 3 𝑖𝑠 𝑎𝑛 𝑒𝑖𝑔𝑒𝑛𝑣𝑎𝑙𝑢𝑒, 𝑎𝑠 𝑡ℎ𝑒𝑟𝑒 𝑎𝑟𝑒 𝑓𝑟𝑒𝑒 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠

Answer
Eigenspace = the set of all solutions of the equation (A- λI)x = 0. In other words, it is the null space of
the matrix A- λI. Put differently, it is all of the eigenvectors that correspond to some eigenvalue. Hence,
we must write the matrix from the previous slide in terms of free variables (general solution) to obtain
the basis for the eigenspace:
𝑥 =
𝑥1
𝑥2
𝑥3
=
1
2
𝑥" − 3𝑥#
𝑓𝑟𝑒𝑒
𝑓𝑟𝑒𝑒
= 𝑥"
a
1
2
1
0
+ 𝑥#
−3
0
1
∴ 𝑒𝑖𝑔𝑒𝑛𝑣𝑒𝑐𝑡𝑜𝑟𝑠 =
a
1
2
1
0
,
−3
0
1
63
Answer
𝐵𝑎𝑠𝑖𝑠 𝑓𝑜𝑟 𝐸𝑖𝑔𝑒𝑛𝑠𝑝𝑎𝑐𝑒 =
a
1
2
1
0
,
−3
0
1

Diagonalization
64

Answers
Question
Exam Time!
Find the characteristic equation of A:
A =
3 2 −1
0 4 2
0 0 1
65
Characteristic equation = the scalar equation det(A- λI) = 0 and is another way of finding the
eigenvalues of a matrix. Hence, we must compute the matrix A- λI and find the determinant of it:
A− λI =
3 2 −1
0 4 2
0 0 1
−
λ 0 0
0 λ 0
0 0 λ
=
3 − λ 2 −1
0 4 − λ 2
0 0 1 − λ
𝑑𝑒𝑡 A− λI = A− λI = 3 − λ 4 − λ 1 − λ = 0
Recall determinant of a triangular matrix (see slide 36). Solving for λ gives us the eigenvalues of A.

Diagonalization - Explanation
Answer
A square matrix A is said to be diagonalizable if A is similar to a diagonal matrix, where A = PDP-1 for
some invertible matrix P and some diagonal matrix D.
The invertible matrix P is the matrix constructed from the eigenvectors of A, and the diagonal matrix is
the matrix which has the eigenvalues of A on its diagonals.
An 𝑛×𝑛 matrix is only diagnosable if A has n linearly independent eigenvectors, which is required to be
able to generate an invertible matrix P. It is important to remember that eigenvectors from different
eigenvalues are always linearly independent.
Hence, if the n eigenvalues are all distinct (different from each other) and have a multiplicity = 1, A is
always diagnosable. If the eigenvalues are not all distinct, A is not always diagonalisable – it depends
on how many linearly independent vectors there are in the eigenspace of the eigenvalues with
multiplicity >1.
Generally, dim 𝑁𝑢𝑙𝑙(A− λI) ≤ multiplicity of λ. If dim 𝑁𝑢𝑙𝑙(A− λI) = multiplicity of λ, A is diagonalizable.
However, if dim 𝑁𝑢𝑙𝑙(A− λI) < multiplicity of λ, A is not diagonalizable.
All in all, for a matrix to be diagonalizable, the sum of the dimensions of the eigenspaces must be equal
to n (the size of A, or the number of eigenvalues).
Tip: to avoid computing P-1 in an exercise you can also check if AP = PD
66

Diagonalization - Explanation
Answer
67
Is 𝐴!×!
diagonalizable?
Are the n
eigenvalues all
distinct?
A = PDP-1
Yes
No
Is the sum of the
dimensions of the
eigenspaces equal
to n?
A = PDP-1
Yes No
A ≠ PDP-1

Answers
Question
Exam Time!
If possible, diagonalize the following matrix:
𝐴 =
1 2
0 2
68
The eigenvalues of a triangular matrix are the entries on its main diagonal (see slide 65). We could have
also used the characteristic equation to find the following eigenvalues:
λ! = 1, λ" = 2
λ! ≠ λ", in other words, they are distinct. Hence, A is diagonalizable.

Answer
D = matrix with eigenvalues of A on its diagonals:
𝐷 =
1 0
0 2
P = matrix constructed from the eigenvectors of A; hence we must compute the eigenspaces of λ!and
2 and select an eigenvector from each eigenspace (𝑁𝑢𝑙𝑙(𝐴 − λ𝐼)) (Note: the order of the eigenvectors in
P does not necessarily matter, as long as it lines up with the eigenvalues in D).
69
Answer
𝐸𝑖𝑔𝑒𝑛𝑠𝑝𝑎𝑐𝑒 𝑜𝑓 λ! = 1:
𝑁𝑢𝑙𝑙 𝐴 − 1𝐼 =
1 2
0 2
−
1 0
0 1
=
0 2
0 1
~
0 1
0 0
𝑥 =
𝑥!
𝑥"
= 𝑥!
1
0
→ 𝑒𝑖𝑔𝑒𝑛𝑠𝑝𝑎𝑐𝑒 =
1
0
→ 𝑣! =
1
0

Answer
𝐸𝑖𝑔𝑒𝑛𝑠𝑝𝑎𝑐𝑒 𝑜𝑓 λ" = 2:
1 2
0 2
−
2 0
0 2
=
−1 2
0 0
𝑥 =
𝑥!
𝑥"
= 𝑥"
2
1
2
1
→ 𝑣" =
2
1
70
Answer
𝑃 = 𝑣! 𝑣" =
1 2
0 1
𝑃*! =
1
det(𝑃)
1 −2
0 1
=
1 −2
0 1
(see slide 41 for inverse of a 2 x 2 matrix)
𝑃𝐷𝑃*! =
1 2
0 1
0
1 0
0 2
0
1 −2
0 1
=
1 2
0 2
= 𝐴

Answers
Question
Exam Time!
If possible, find some invertible matrix P and some diagonal matrix D such that A = PDP-1 , for the
following matrix A:
𝐴 =
−1 0 −2
0 2 0
3 0 4
71
Find the characteristic equation, to determine the following eigenvalues:
𝑑𝑒𝑡 A− λI = A− λI = 0 = 𝑑𝑒𝑡
−1 − λ 0 −2
0 2 − λ 0
3 0 4 − λ
Use cofactor expansion along the second row (see slide 34).

Answer
𝑑𝑒𝑡 A− λI = (2 − λ) 0
−1 − λ −2
3 4 − λ
= (2 − λ) −1 − λ 4 − λ + 6 = (2 − λ) λ − 2 λ − 1 = 0
λ = 1 (multiplicity 1), λ = 2 (multiplicity 2)
Now, as the eigenvalues are not distinct, we are not exactly sure if A is diagonalizable. We will solve for
a basis for our 2 eigenspaces.
72
Answer
𝐸𝑖𝑔𝑒𝑛𝑠𝑝𝑎𝑐𝑒 𝑜𝑓 λ! = 2:
−1 0 −2
0 2 0
3 0 4
−
2 0 0
0 2 0
0 0 2
=
−3 0 −2
0 0 0
3 0 2
~
1 0 a
2
3
0 0 0
0 0 0
𝑥 =
𝑥!
𝑥"
𝑥#
= 𝑥"
0
1
0
+ 𝑥#
a
−2
3
0
1
0
1
0
,
a
−2
3
0
1
→ 𝑣! =
0
1
0
, 𝑣" =
a
−2
3
0
1

Answer
As we can now see, there were 2 free variables, telling us that the matrix is diagonalizable as the
eigenspace corresponding to λ! = 2 is two-dimensional. In other words, we were able to find two
linearly independent vectors (𝑣! and 𝑣") that form a basis for the eigenspace.
This means, after finding our third eigenvector 𝑣# which will be done below, the sum of the dimensions
of the eigenspaces will be equal to 3.
73
Answer
𝐸𝑖𝑔𝑒𝑛𝑠𝑝𝑎𝑐𝑒 𝑜𝑓 λ" = 1:
−1 0 −2
0 2 0
3 0 4
−
1 0 0
0 1 0
0 0 1
=
−2 0 −2
0 1 0
3 0 3
~
1 0 1
0 1 0
0 0 0
𝑥 =
𝑥!
𝑥"
𝑥#
= 𝑥#
−1
0
1
−1
0
1
→ 𝑣# =
−1
0
1
Now, we found our third linearly independent eigenvector of A.

Answer
D = matrix with eigenvalues of A on its diagonals:
𝐷 =
2 0 0
0 2 0
0 0 1
74
Answer
P = matrix constructed from the eigenvectors of A:
𝑃 =
0 − a
2
3 −1
1 0 0
0 1 1

LA question Pool

More Related Content

Similar to LA question Pool

Recently uploaded

LA question Pool