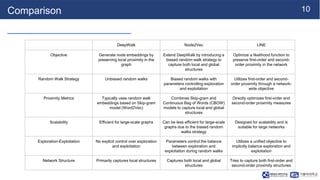
LINE is a network embedding algorithm that learns distributed representations of nodes in a graph. It aims to preserve both first-order and second-order proximity structures by optimizing an objective function. The algorithm is efficient and can learn embeddings for networks with millions of nodes and billions of edges. Empirical experiments on language, social, and citation networks demonstrate LINE's effectiveness at capturing network structures.