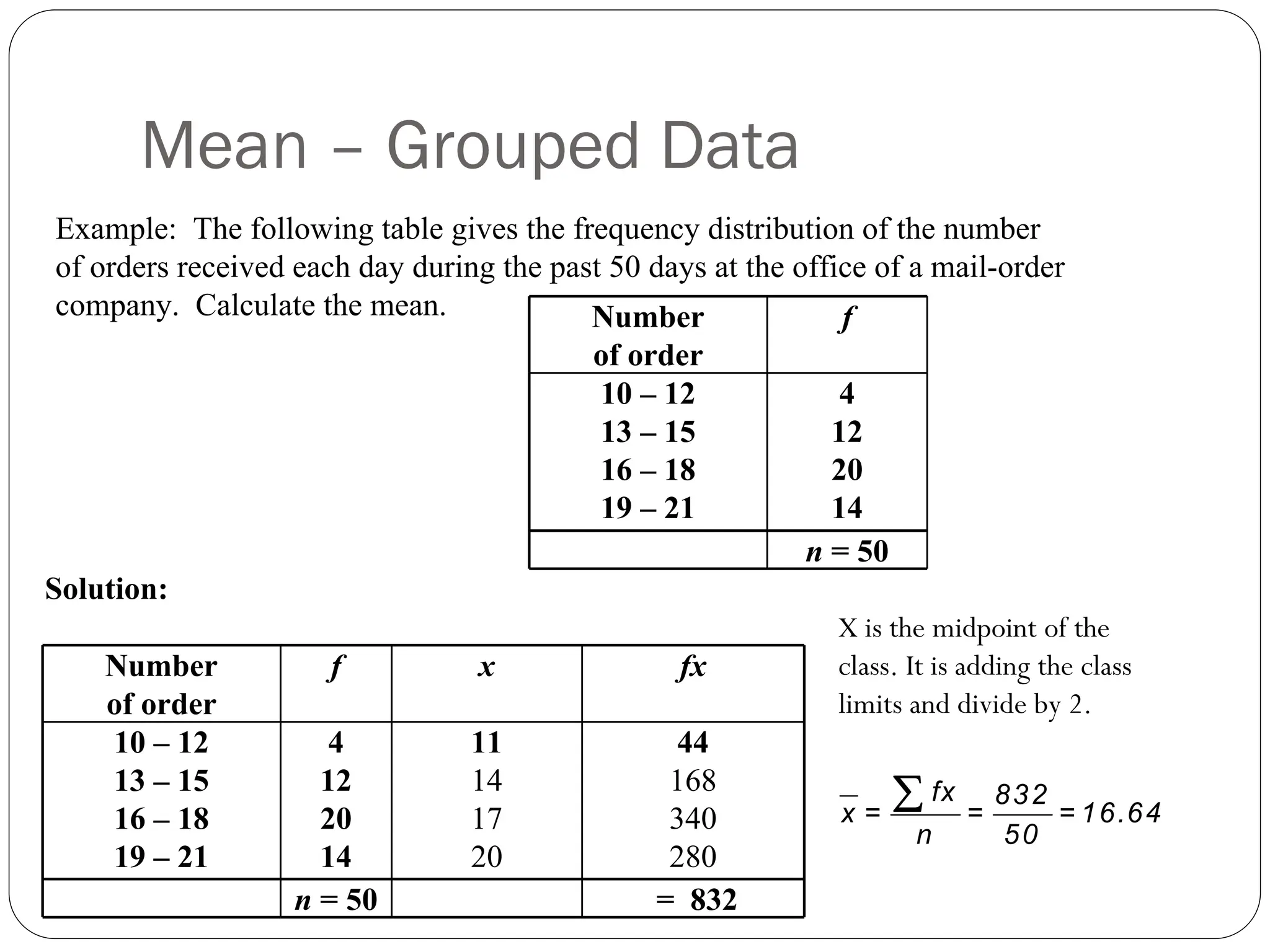
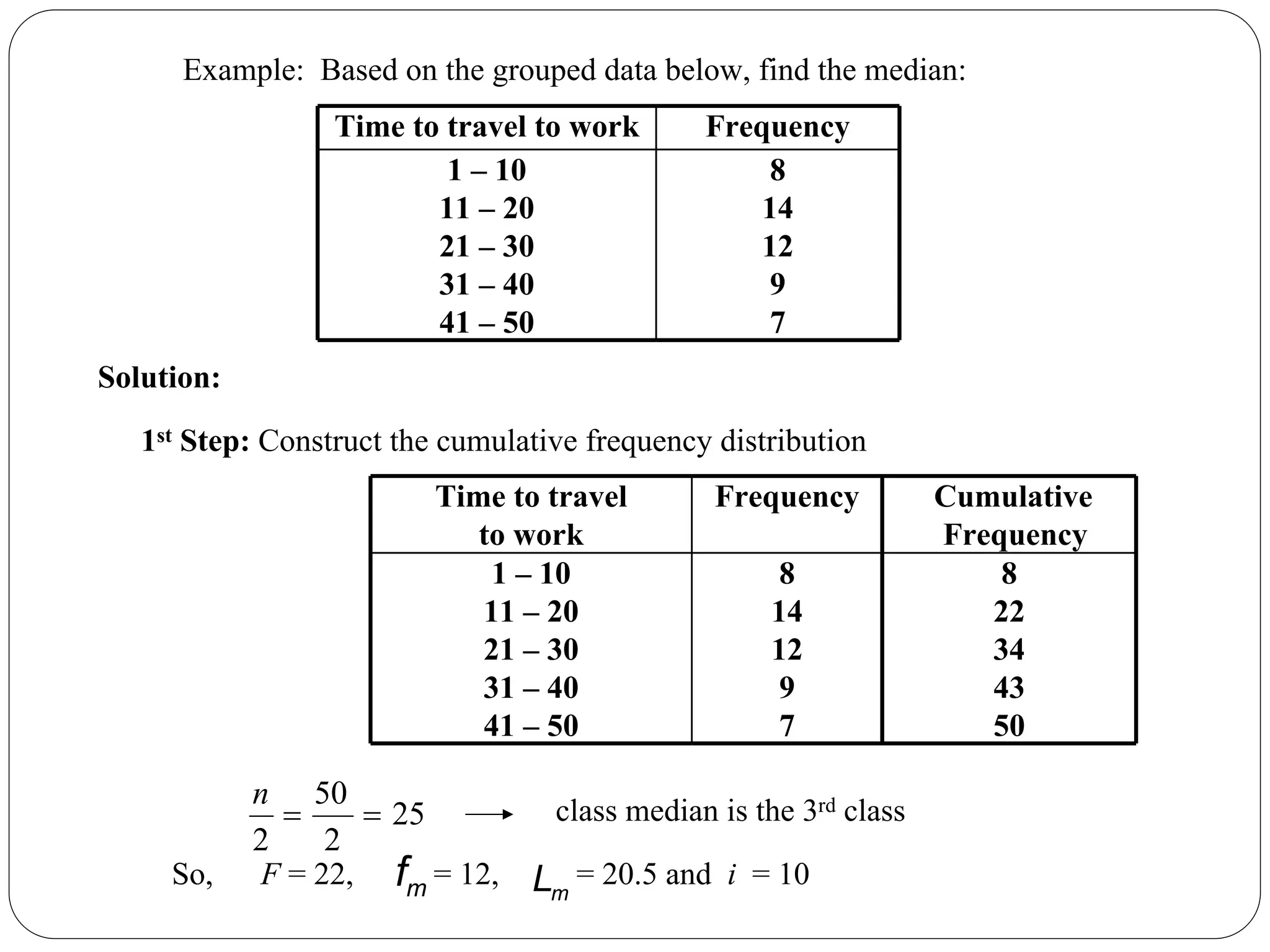
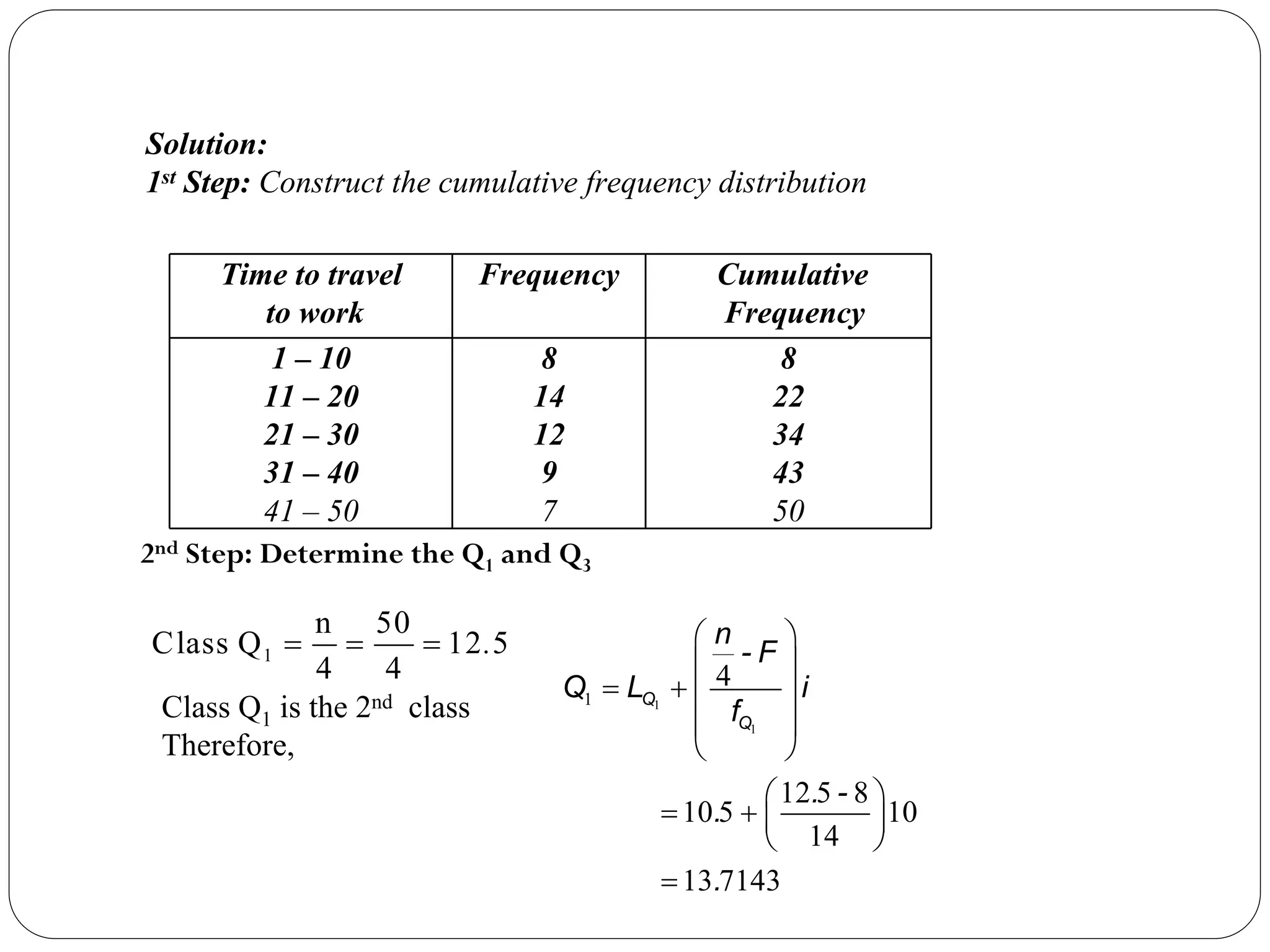
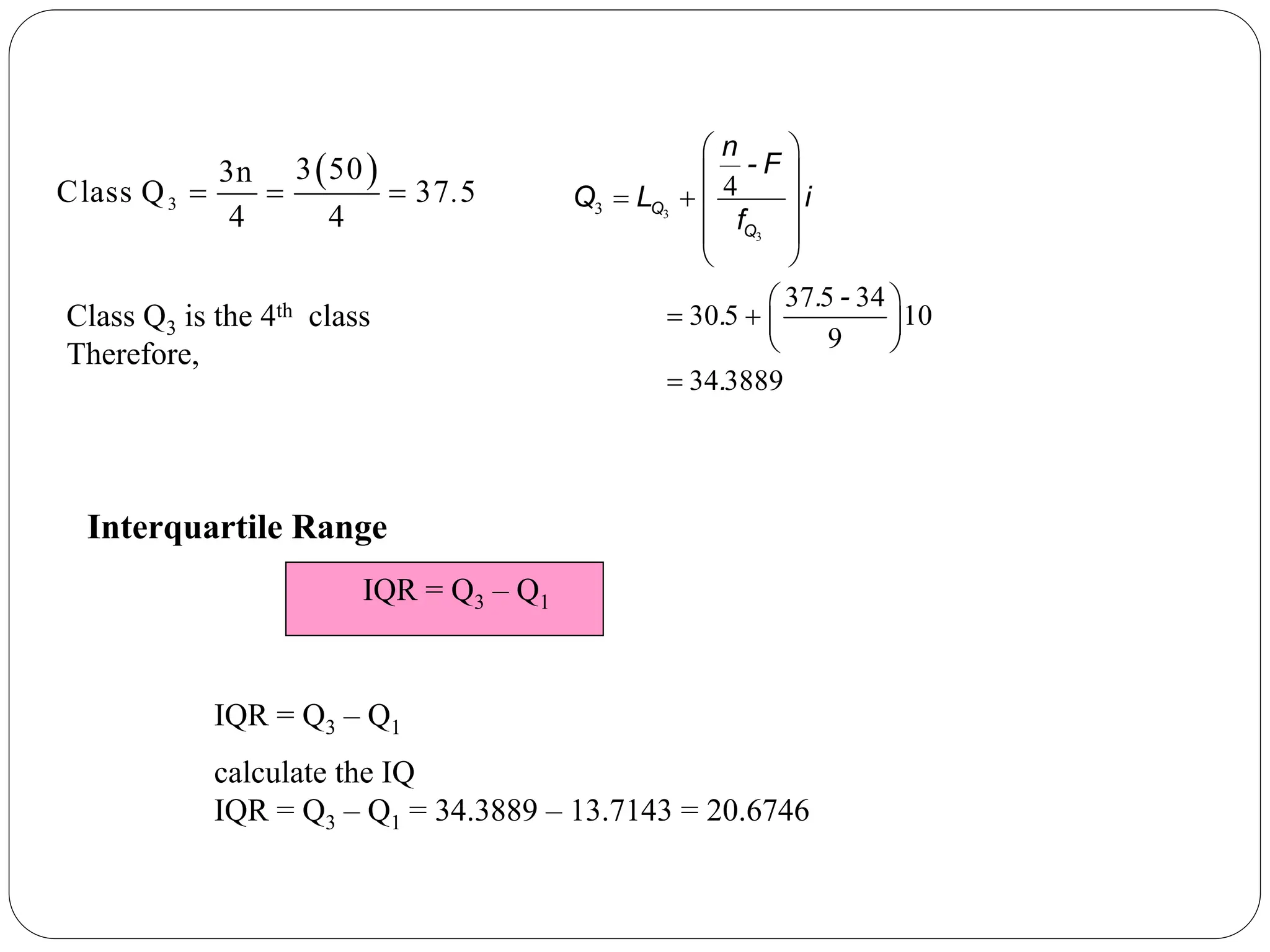
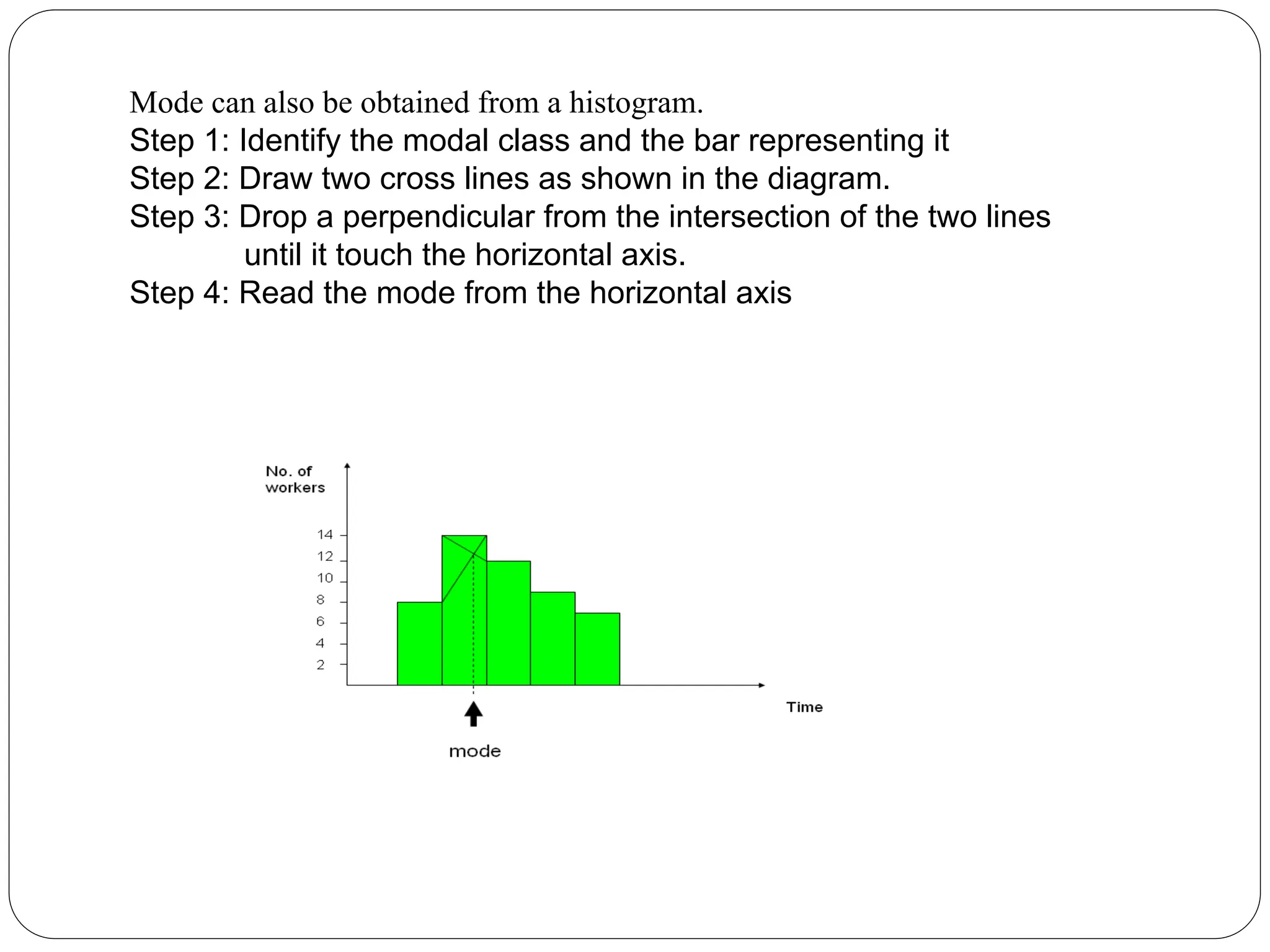
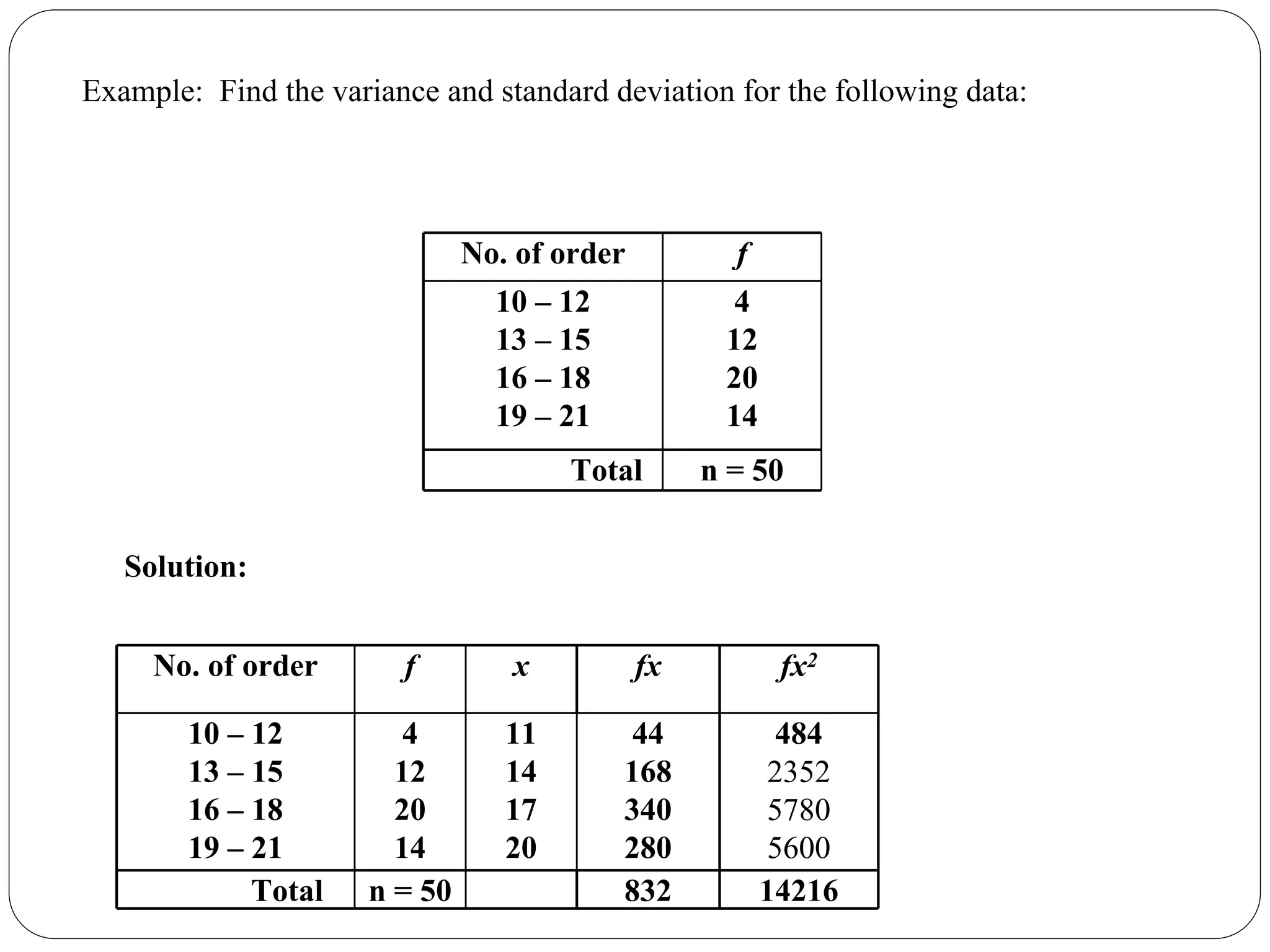
The document discusses statistical concepts including mean, median, mode, quartiles, and interquartile range, specifically for grouped data. It provides step-by-step methods for calculating these metrics using cumulative frequency distributions and formulas. Additionally, it offers examples related to frequency distribution of orders and time to travel to work to illustrate the calculations.

1. 1. Mean, Median and Mode
2. First Quantile, third Quantile and
Interquantile Range.
Lecture 2 – Grouped Data
Calculation

2. Mean – Grouped Data
Number
of order
f
10 – 12
13 – 15
16 – 18
19 – 21
4
12
20
14
n = 50
Number
of order
f x fx
10 – 12
13 – 15
16 – 18
19 – 21
4
12
20
14
11
14
17
20
44
168
340
280
n = 50 = 832
fx 832
x = = = 16.64
n 50
∑
Example: The following table gives the frequency distribution of the number
of orders received each day during the past 50 days at the office of a mail-order
company. Calculate the mean.
Solution:
X is the midpoint of the
class. It is adding the class
limits and divide by 2.

3. Median and Interquartile Range
– Grouped Data
Step 1: Construct the cumulative frequency distribution.
Step 2: Decide the class that contain the median.
Class Median is the first class with the value of cumulative
frequency equal at least n/2.
Step 3: Find the median by using the following formula:
M e d ia n
⎛ ⎞
⎜ ⎟
⎜ ⎟
⎜ ⎟
⎝ ⎠
m
m
n
- F
2
= L + i
f
m
L
m
f
Where:
n = the total frequency
F = the cumulative frequency before class median
i = the class width
= the lower boundary of the class median
= the frequency of the class median

4. Time to travel to work Frequency
1 – 10
11 – 20
21 – 30
31 – 40
41 – 50
8
14
12
9
7
Example: Based on the grouped data below, find the median:
Solution:
Time to travel
to work
Frequency Cumulative
Frequency
1 – 10
11 – 20
21 – 30
31 – 40
41 – 50
8
14
12
9
7
8
22
34
43
50
25
2
50
2
=
=
n
m
f m
L
1st Step: Construct the cumulative frequency distribution
class median is the 3rd class
So, F = 22, = 12, = 20.5 and i = 10

5. Therefore,
2
25 22
21 5 10
12
24
⎛ ⎞
⎜ ⎟
+ ⎜ ⎟
⎜ ⎟
⎝ ⎠
⎛ ⎞
+ ⎜ ⎟
⎝ ⎠
Median
=
=
m
m
n
- F
= L i
f
-
.
Thus, 25 persons take less than 24 minutes to travel to work and another 25 persons
take more than 24 minutes to travel to work.

6. 1
1
1 Q
Q
n
- F
4
Q L + i
f
⎛ ⎞
⎜ ⎟
= ⎜ ⎟
⎜ ⎟
⎝ ⎠
⎛ ⎞
⎜ ⎟
= ⎜ ⎟
⎜ ⎟
⎝ ⎠
3
3
3 Q
Q
3 n
- F
4
Q L + i
f
Quartiles
Using the same method of calculation as in the Median,
we can get Q1 and Q3 equation as follows:
Time to travel to work Frequency
1 – 10
11 – 20
21 – 30
31 – 40
41 – 50
8
14
12
9
7
Example: Based on the grouped data below, find the Interquartile Range

7. Time to travel
to work
Frequency Cumulative
Frequency
1 – 10
11 – 20
21 – 30
31 – 40
41 – 50
8
14
12
9
7
8
22
34
43
50
1
n 50
Class Q 12 5
4 4
.
= = =
1
1
1
4
12 5 8
10 5 10
14
13 7143
⎛ ⎞
⎜ ⎟
= + ⎜ ⎟
⎜ ⎟
⎝ ⎠
⎛ ⎞
= + ⎜ ⎟
⎝ ⎠
=
Q
Q
n
- F
Q L i
f
. -
.
.
Solution:
1st Step: Construct the cumulative frequency distribution
Class Q1 is the 2nd class
Therefore,
2nd Step: Determine the Q1 and Q3

8. ( )
3
3 50
3n
Class Q 37 5
4 4
.
= = =
3
3
3
4
37 5 34
30 5 10
9
34 3889
⎛ ⎞
⎜ ⎟
= + ⎜ ⎟
⎜ ⎟
⎝ ⎠
⎛ ⎞
= + ⎜ ⎟
⎝ ⎠
=
Q
Q
n
- F
Q L i
f
. -
.
.
IQR = Q3 – Q1
Class Q3 is the 4th class
Therefore,
Interquartile Range
IQR = Q3 – Q1
calculate the IQ
IQR = Q3 – Q1 = 34.3889 – 13.7143 = 20.6746

9. Mode
•Mode is the value that has the highest frequency in a data set.
•For grouped data, class mode (or, modal class) is the class with the highest frequency.
•To find mode for grouped data, use the following formula:
⎛ ⎞
⎜ ⎟
⎝ ⎠
M o d e 1
m o
1 2
Δ
= L + i
Δ + Δ
Mode – Grouped Data
mo
L
1
Δ
2
Δ
Where:
is the lower boundary of class mode
is the difference between the frequency of class mode
and the frequency of the class before the class mode
is the difference between the frequency of class mode and the frequency
of the class after the class mode
i is the class width

10. Calculation of Grouped Data - Mode
Time to travel to work Frequency
1 – 10
11 – 20
21 – 30
31 – 40
41 – 50
8
14
12
9
7
Example: Based on the grouped data below, find the mode
mo
L 1
Δ 2
Δ
6
1 0 5 1 0 1 7 5
6 2
⎛ ⎞
+ =
⎜ ⎟
+
⎝ ⎠
M o d e = . .
Solution:
Based on the table,
= 10.5, = (14 – 8) = 6, = (14 – 12) = 2 and
i = 10

11. Mode can also be obtained from a histogram.
Step 1: Identify the modal class and the bar representing it
Step 2: Draw two cross lines as shown in the diagram.
Step 3: Drop a perpendicular from the intersection of the two lines
until it touch the horizontal axis.
Step 4: Read the mode from the horizontal axis

12. ( )
2
2
2
−
σ =
∑
∑
fx
fx
N
N
( )
2
2
2
1
−
=
−
∑
∑
fx
fx
n
s
n
2
2
σ
σ =
2
2
s
s =
Population Variance:
Variance for sample data:
Standard Deviation:
Population:
Sample:
Variance and Standard Deviation
-Grouped Data

13. No. of order f
10 – 12
13 – 15
16 – 18
19 – 21
4
12
20
14
Total n = 50
No. of order f x fx fx2
10 – 12
13 – 15
16 – 18
19 – 21
4
12
20
14
11
14
17
20
44
168
340
280
484
2352
5780
5600
Total n = 50 832 14216
Example: Find the variance and standard deviation for the following data:
Solution:

14. ( )
( )
2
2
2
2
1
832
14216
50
50 1
7 5820
−
=
−
−
=
−
=
∑
∑
fx
fx
n
s
n
.
75
.
2
5820
.
7
2
=
=
= s
s
Variance,
Standard Deviation,
Thus, the standard deviation of the number of orders received at
the office of this mail-order company during the past 50 days is 2.75.