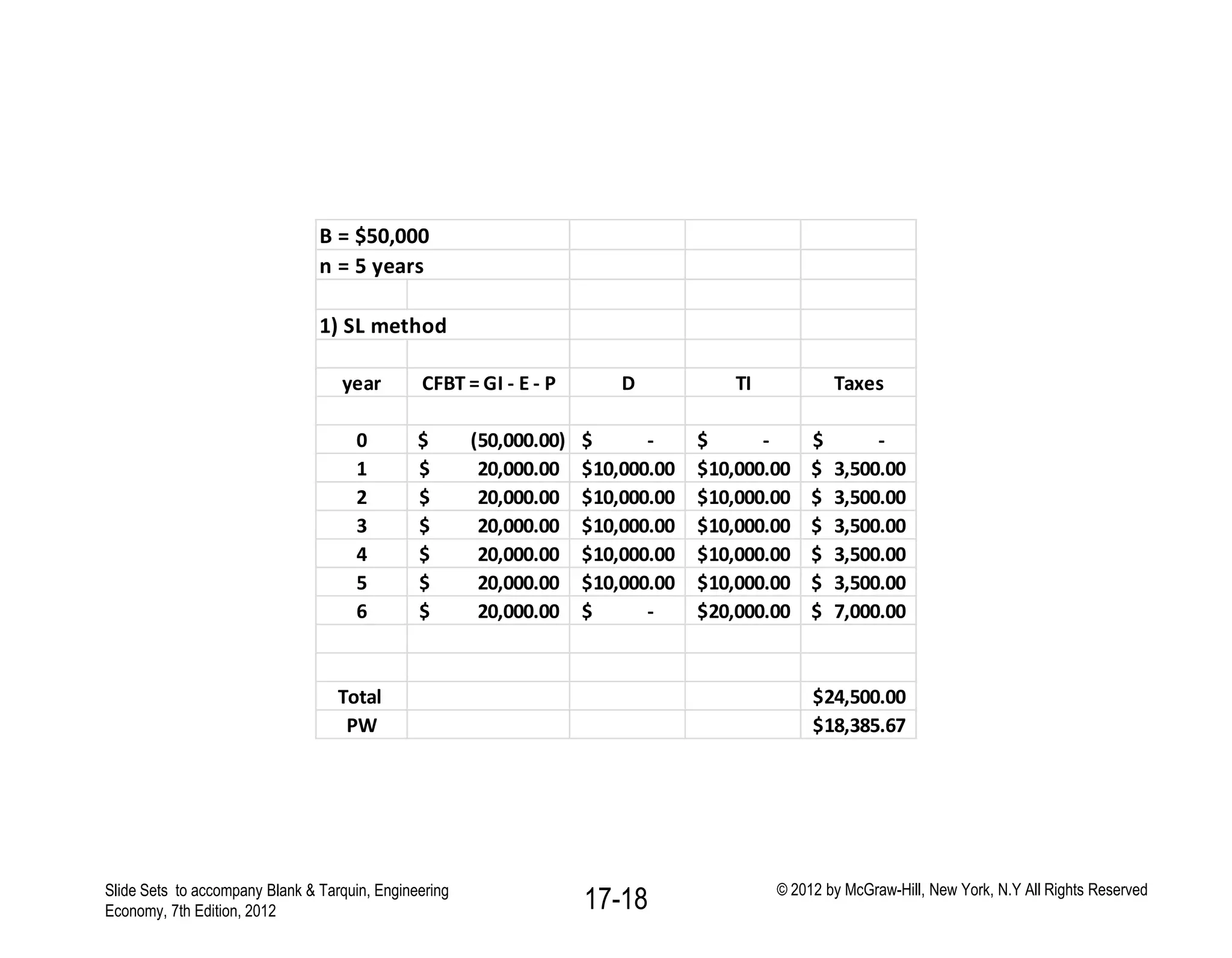
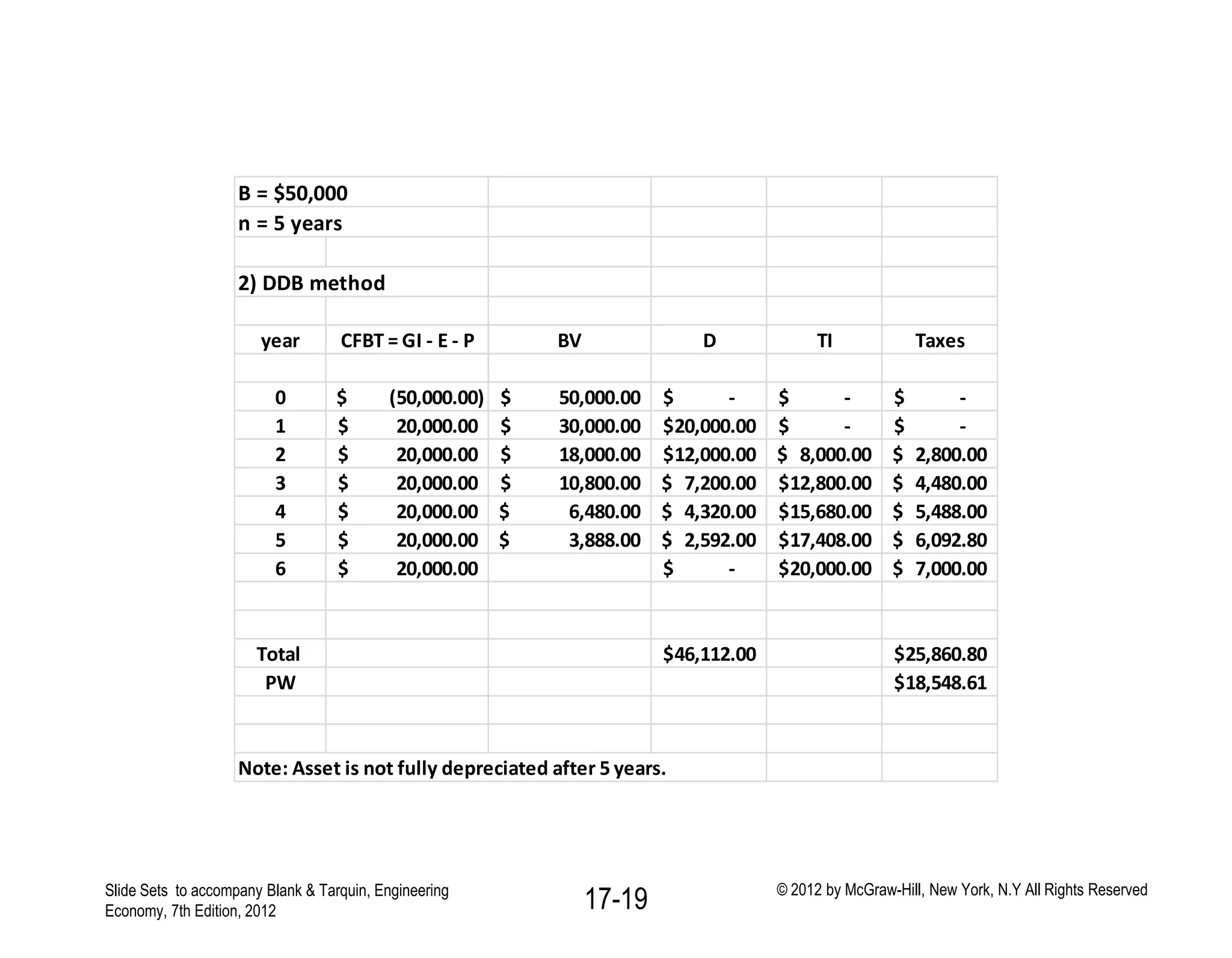
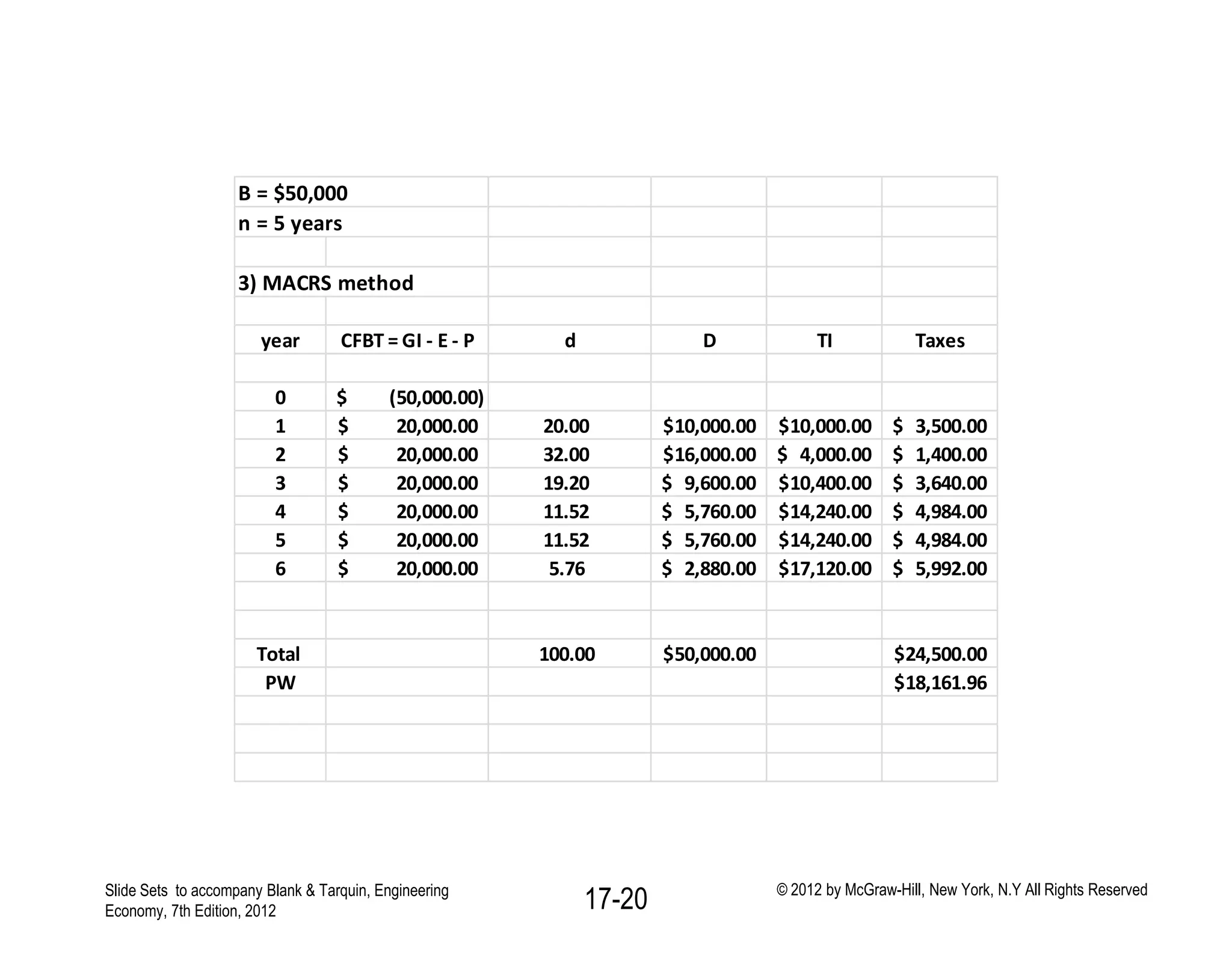
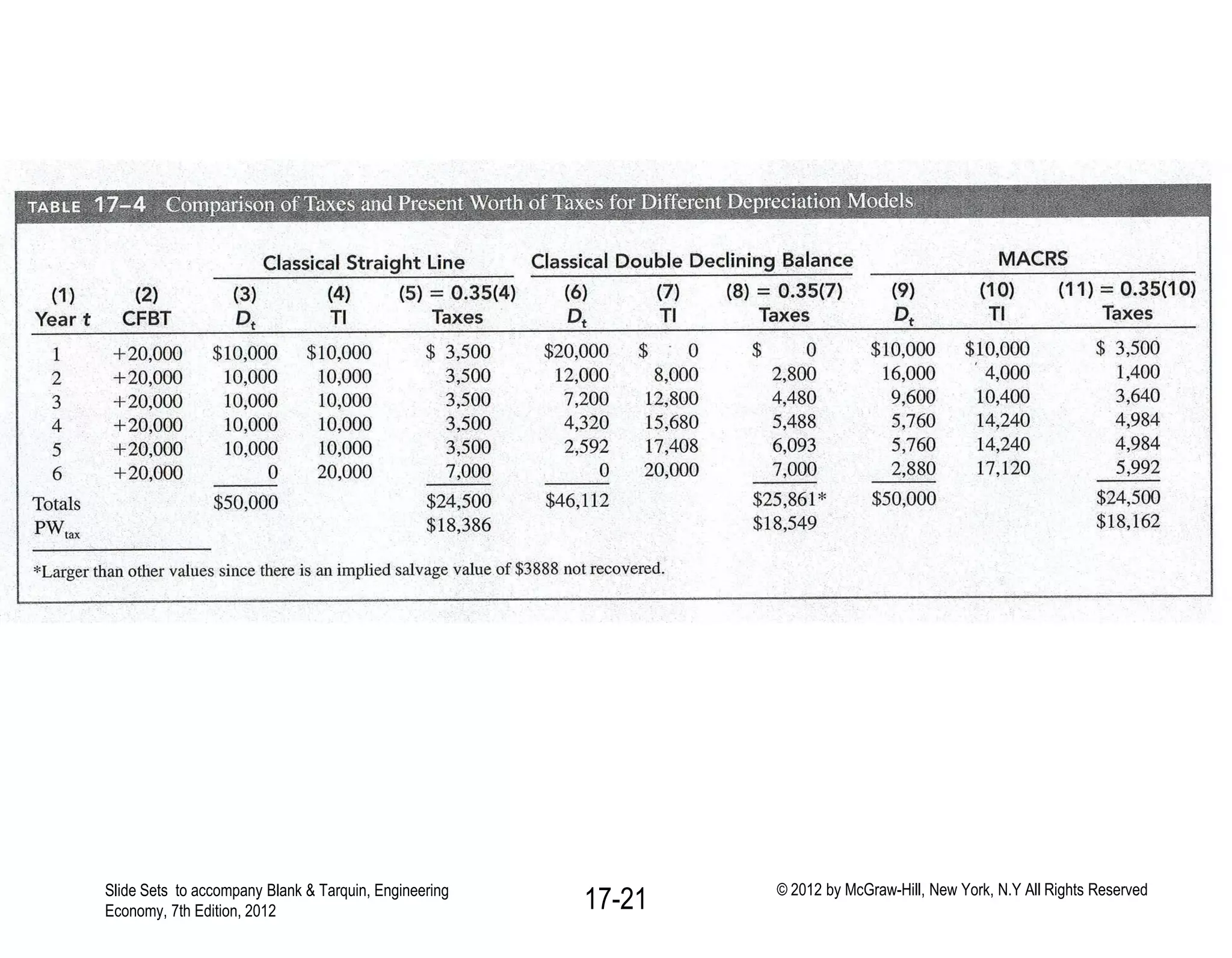
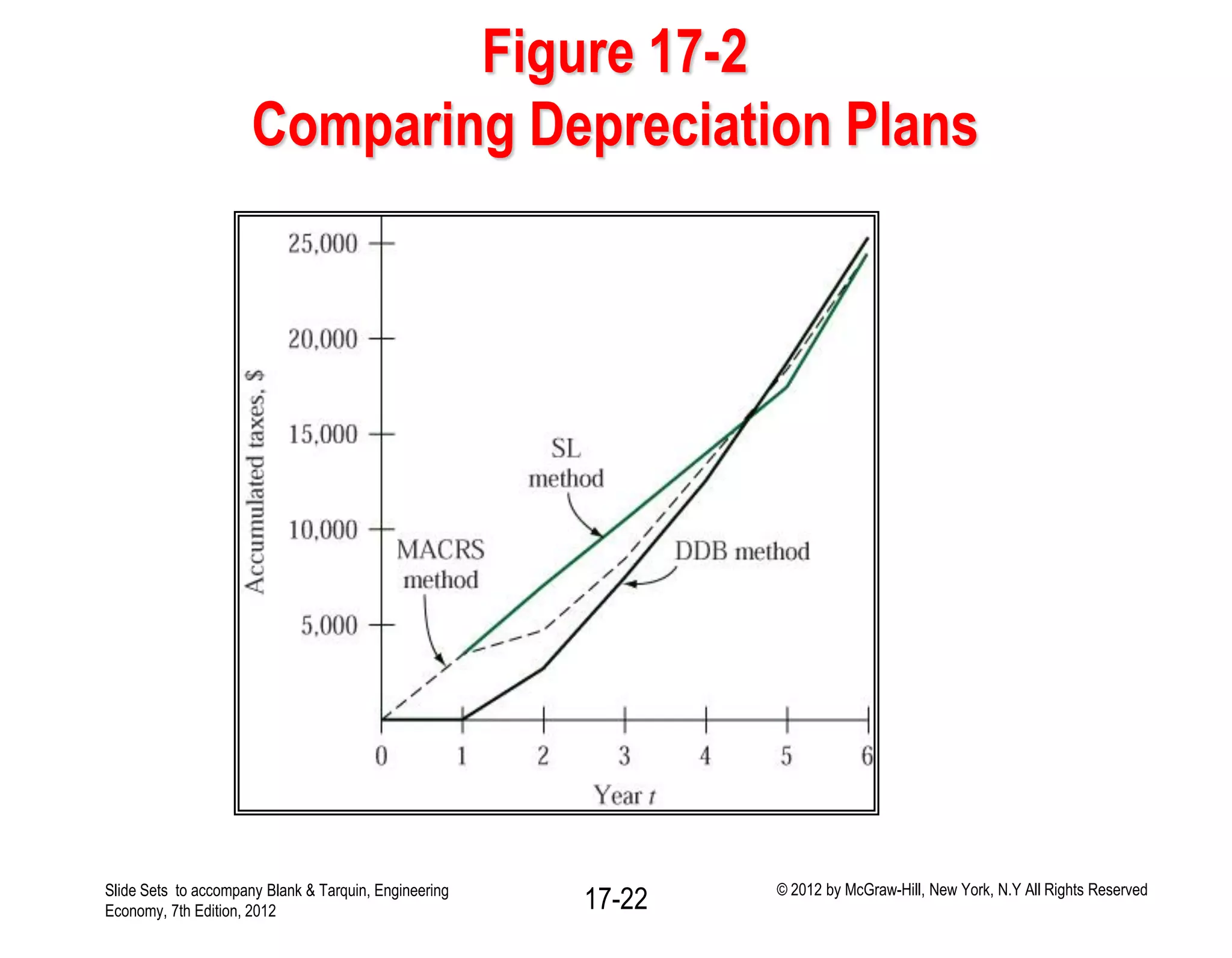
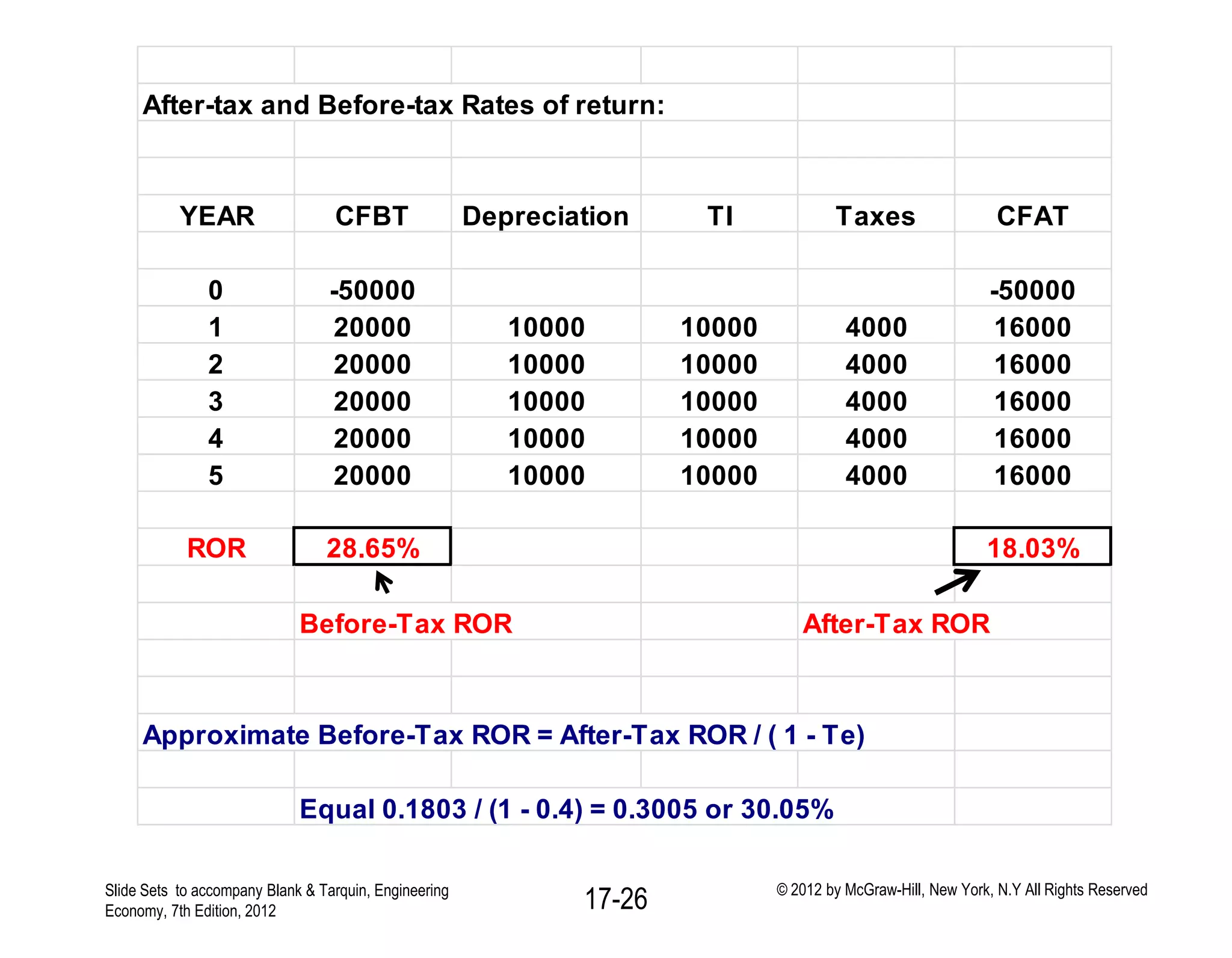
This document discusses concepts related to corporate income taxes and cash flow analysis. It defines key terms like gross income, taxable income, depreciation, taxes owed, and net profit after tax. It also discusses how to calculate cash flow before taxes and after taxes for each year of a project. The document provides an example cash flow analysis for a project using straight-line, double declining balance, and MACRS depreciation methods to demonstrate how different depreciation approaches can affect taxes paid over the life of a project. It emphasizes that accelerated depreciation methods and shorter recovery periods can lower the present value of total taxes paid.

1. Lecture # 9
Cost Estimation
Taxes and Economic Value
added (EVA)
17-1 Dr. A. Alim

2. Income Tax Terminology and Relations for
Corporations (and Individuals)
 Gross Income
 Total income for the tax
year from all revenue
producing function of
the enterprise.
 Sales revenues,
 Fees,
 Rent,
 Royalties,
 Sale of assets
 Income Tax
 The total amount of money
transferred from the
enterprise to the various
taxing agencies for a given
tax year.
 Federal corporate taxes are
normally paid at the end of
every quarter and a final
adjusting payment is
submitted with the tax return
at the end of the fiscal year.
 This tax is based upon the
income producing power of
the firm.
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-2 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

3. Terms - continued
 Operating Expenses
 All legally recognized
costs associated with
doing business for the tax
year.
 Real cash flows.
 Taxable Income
 Calculated amount of
money for a specified
time period from
which the tax liability
is determined.
 Calculated as:
 TI = Gross Income –
expenses –
depreciation
TI = GI – E – D
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-3 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

4. Terms - continued
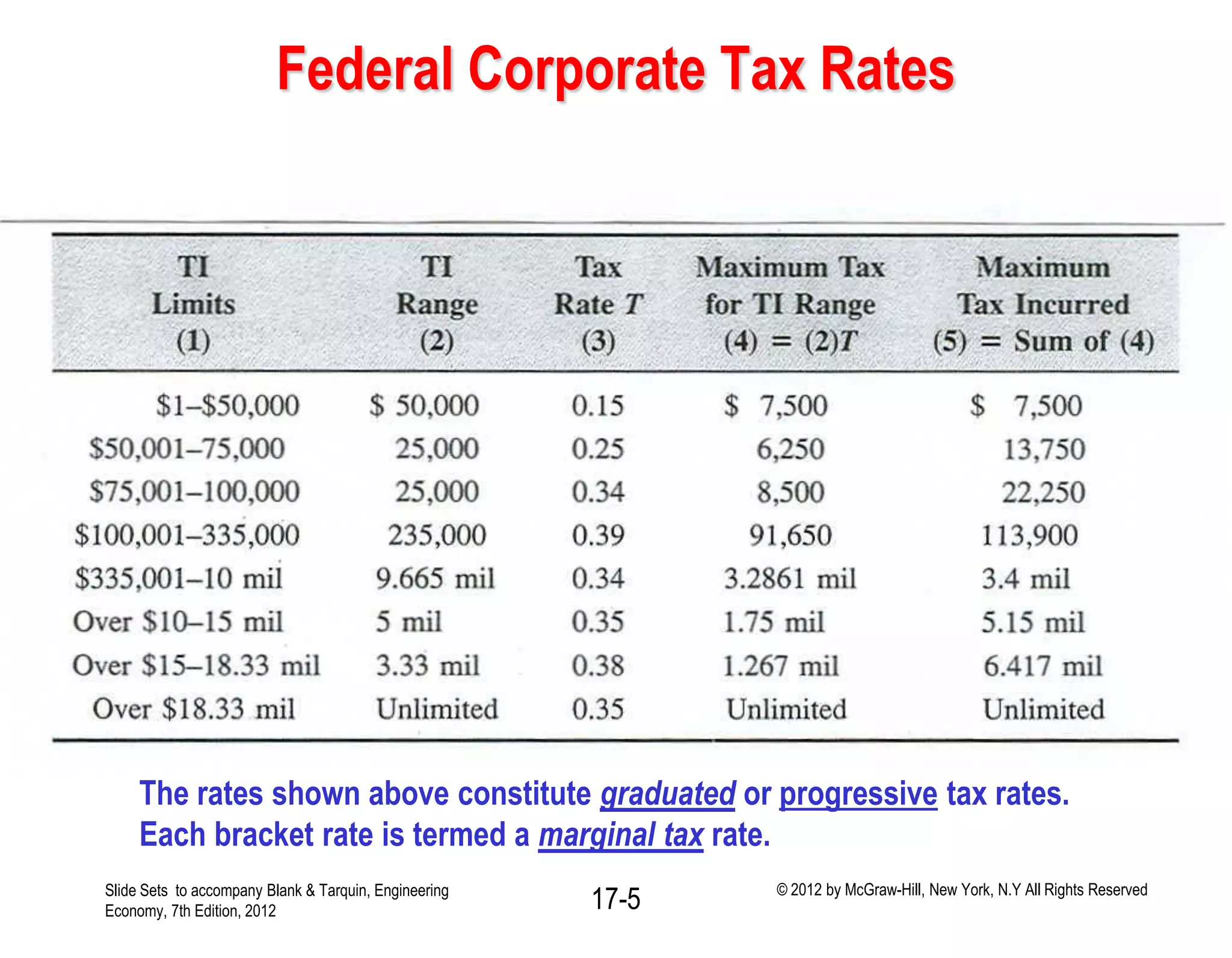
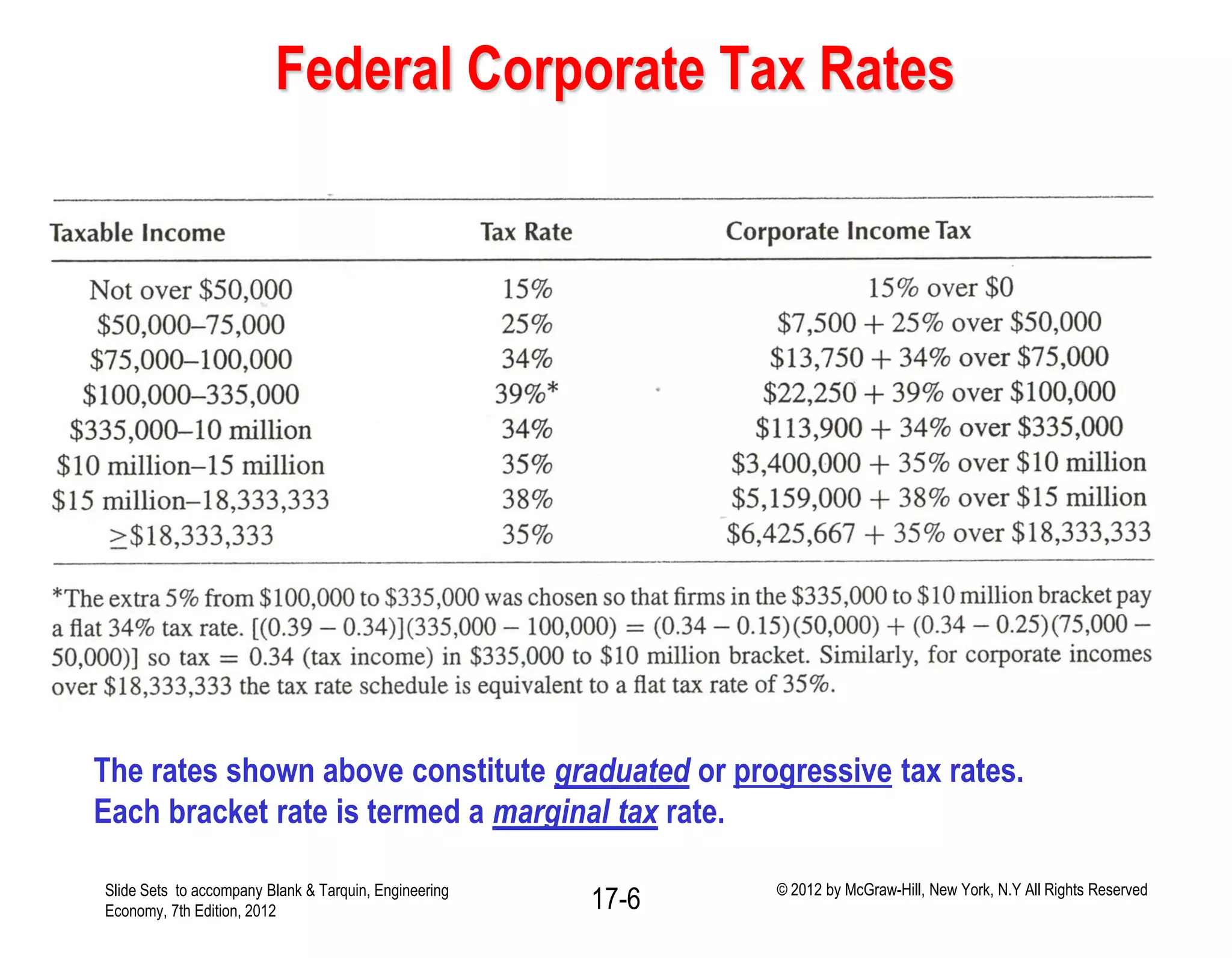
 Tax rate T
 A percentage or decimal
equivalent of TI.
 For Federal corporate income
tax T is represented by a series
of tax rates.
 The applicable tax rate depends
upon the total amount of TI.
 Taxes owed equals:
 Taxes = (taxable income) x
(applicable rate)
 = (TI)(T).
 Net Profit After Tax (NPAT)
 Amount of money remaining each year
when income taxes are subtracted from
taxable income.
NPAT = TI – {(TI)(T)}
= (TI)(1-T)
 Effective tax rate Te combines federal and local
rates:
Total Tax = Federal tax + State tax
State tax is deductable from taxable federal
income, hence : if Tf is federal tax rate, Ts is
state tax rate, and Te is total effective tax rate:
TI (Te ) = TI(Ts) + [TI - TI(Ts)] (Tf)
Te = Tf + Ts – TfTs or Te = Ts + (1-Ts) Tf
Te = Tf + (1-Tf) Ts
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-4 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

5. Federal Corporate Tax Rates
The rates shown above constitute graduated or progressive tax rates.
Each bracket rate is termed a marginal tax rate.
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-5 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

6. Federal Corporate Tax Rates
The rates shown above constitute graduated or progressive tax rates.
Each bracket rate is termed a marginal tax rate.
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-6 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

7. Example 17.1, page 572, Blank (6th ed.)
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-7 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

8. International Corporate Tax rates (2011)
Tax rate %
≥ 35
25 - 35
10 - 25
≤ 10
Country
USA, Argentina
Germany, France, Spain, Australia, UK.
Russia, China, Canada, Hungary, UAE
Serbia, Bulgaria, Montenegro
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-8 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

9. Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012
© 2012 by McGraw-Hill, New York, N.Y All Rights Reserved
17-9
Cash Flow Analysis
Before Taxes and After Taxes

10. Cash Flow Before Tax (CFBT)
FOR ANY ONE YEAR:
 Cash Flow before Tax (CFBT)
 CFBT = gross income – expenses – initial investment (total
capital) + salvage value + recovered working capital (if any)
 = GI – E – P + S + W
appear year 0 year n
in years
1 to n
 CFBT = - P in year zero
 CFBT = GI – E in years 1 to n-1
 CFBT = GI – E + S + W in year n
 (W is recovered working capital, if any)
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-10 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

11. Cash Flow After Tax (CFAT)
FOR ANY ONE YEAR:
 Cash Flow After Tax (CFAT)
 CFAT = CFBT – taxes
 CFAT = [GI – E – P + S + W] – (GI – E – D)(Te)
 CFAT = NPAT + D Valid for all years except years 0 and n !
Note: only fixed capital is depreciable, if there is no working capital
then by definition total capital is fixed and is depreciable.
 An evaluation format:
 Table 17.2 , p. 449, Blank (7th ed.)
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-11 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

12. Table column Headings for Calculation of
CFBT and CFAT
Important Notes:
*) E and P are always negative values.
*) S and possibly working capital (W) appear in last year as positive values
*) P,S, and W appear only in CFBT and CFAT, never in TI.
*) Only fixed capital is depreciated.
*) In a given year, if the depreciation is larger than (GI-E), TI will be
negative resulting in a negative tax, or tax credit.
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-12 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved
Plus working capital W , if any
Of fixed capital only !

13. Calculation of CFBT and CFAT
Example 17.3, page 576, Blank (6th ed.)
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-13 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

14. Example 17.3
YEAR GI E P and S CFBT d D TI TAXES CFAT
0 $0 $0 -$550,000 -$550,000 $0 $0 $0 -$550,000
1 $200,000 -$90,000 $110,000 0.2000 $110,000 $0 $0 $110,000
2 $200,000 -$90,000 $110,000 0.3200 $176,000 -$66,000 -$23,100 $133,100
3 $200,000 -$90,000 $110,000 0.1920 $105,600 $4,400 $1,540 $108,460
4 $200,000 -$90,000 $110,000 0.1152 $63,360 $46,640 $16,324 $93,676
5 $200,000 -$90,000 $110,000 0.1152 $63,360 $46,640 $16,324 $93,676
6 $200,000 -$90,000 $150,000 $260,000 0.0576 $31,680 $78,320 $27,412 $232,588
Total $260,000 $550,000 $38,500 $221,500
GI - E - P + S d x 550,000 GI - E - D 0.35xTI CFBT-Taxes
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-14 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

15. Example 17.3
Y GI - E P and S CFBT d D TI TAXES CFAT NPAT NPAT + D
0 $0 -$550,000 -$550,000 $0 $0 $0 -$550,000 $0 $0
1 $110,000 $110,000 0.2000 $110,000 $0 $0 $110,000 $0 $110,000
2 $110,000 $110,000 0.3200 $176,000 -$66,000 -$23,100 $133,100 -$42,900 $133,100
3 $110,000 $110,000 0.1920 $105,600 $4,400 $1,540 $108,460 $2,860 $108,460
4 $110,000 $110,000 0.1152 $63,360 $46,640 $16,324 $93,676 $30,316 $93,676
5 $110,000 $110,000 0.1152 $63,360 $46,640 $16,324 $93,676 $30,316 $93,676
6 $110,000 $150,000 $260,000 0.0576 $31,680 $78,320 $27,412 $232,588 $50,908 $82,588
Total $260,000 $550,000 $38,500 $221,500
GI - E - P + S d x 550,000 GI - E - D 0.35xTI CFBT-Taxes TI - Taxes
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-15 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved
Note that CFAT does not equal (NPAT+ D) in year 0 and in the last year. CFAT equals (NPAT+D) only in years 1 to (n-1).

16. Effect on Taxes of Different Depreciation
Methods and Recovery Periods
 Criterion used to compare different depreciation
methods – compute ---
 Objective – Minimize the PW of future taxes paid owing
to a given depreciation method
 For the same salvage value, the total taxes paid are equal for all
depreciation models
 The PW of taxes paid is less for accelerated depreciation methods
 Shorter depreciation periods result in lower PW of future taxes
paid over longer time periods
n
tax
t=1
PW = (taxes in year t)(P/F,i,t)
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-16 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

17. Effect on Taxes of Different Depreciation
Methods and Recovery Periods
Example 17.3, page 451, Blank (7th ed.)
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-17 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

18. Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012
© 2012 by McGraw-Hill, New York, N.Y All Rights Reserved
17-18
B = $50,000
n = 5 years
1) SL method
year CFBT = GI - E - P D TI Taxes
0 (50,000.00)$ -$ -$ -$
1 20,000.00$ 10,000.00$ 10,000.00$ 3,500.00$
2 20,000.00$ 10,000.00$ 10,000.00$ 3,500.00$
3 20,000.00$ 10,000.00$ 10,000.00$ 3,500.00$
4 20,000.00$ 10,000.00$ 10,000.00$ 3,500.00$
5 20,000.00$ 10,000.00$ 10,000.00$ 3,500.00$
6 20,000.00$ -$ 20,000.00$ 7,000.00$
Total 24,500.00$
PW 18,385.67$

19. Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012
© 2012 by McGraw-Hill, New York, N.Y All Rights Reserved
17-19
B = $50,000
n = 5 years
2) DDB method
year CFBT = GI - E - P BV D TI Taxes
0 (50,000.00)$ 50,000.00$ -$ -$ -$
1 20,000.00$ 30,000.00$ 20,000.00$ -$ -$
2 20,000.00$ 18,000.00$ 12,000.00$ 8,000.00$ 2,800.00$
3 20,000.00$ 10,800.00$ 7,200.00$ 12,800.00$ 4,480.00$
4 20,000.00$ 6,480.00$ 4,320.00$ 15,680.00$ 5,488.00$
5 20,000.00$ 3,888.00$ 2,592.00$ 17,408.00$ 6,092.80$
6 20,000.00$ -$ 20,000.00$ 7,000.00$
Total 46,112.00$ 25,860.80$
PW 18,548.61$
Note: Asset is not fully depreciated after 5 years.

20. Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012
© 2012 by McGraw-Hill, New York, N.Y All Rights Reserved
17-20
B = $50,000
n = 5 years
3) MACRS method
year CFBT = GI - E - P d D TI Taxes
0 (50,000.00)$
1 20,000.00$ 20.00 10,000.00$ 10,000.00$ 3,500.00$
2 20,000.00$ 32.00 16,000.00$ 4,000.00$ 1,400.00$
3 20,000.00$ 19.20 9,600.00$ 10,400.00$ 3,640.00$
4 20,000.00$ 11.52 5,760.00$ 14,240.00$ 4,984.00$
5 20,000.00$ 11.52 5,760.00$ 14,240.00$ 4,984.00$
6 20,000.00$ 5.76 2,880.00$ 17,120.00$ 5,992.00$
Total 100.00 50,000.00$ 24,500.00$
PW 18,161.96$

21. Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-21 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

22. Figure 17-2
Comparing Depreciation Plans
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-22 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

23. Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-23 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

24. Cash flow analysis is important in calculating ROR Before tax and
After tax
 The Rate Of Return (ROR) is a general term used to measure profitability.
 There are several ways to define ROR, e.g.:
* If we ignore time value of money, then ROR is known as Return on Invested Capital (ROI),
In this case, ROR = ROI = Net Profit / Invested capital.
* If we include time value of money, for a series of cash flows,
the ROR is known as IRR (internal rate of return) or discounted cash flow rate of return (DCFRR)
 The rate of return ROR can be calculated using the IRR function for a series of cash flows.
 Rate of return (ROR) can be calculated before tax using CFBT analysis, and/or after tax using CFAT
analysis.
 We therefore have a Before – Tax ROR and an After-Tax ROR. Both may be obtained using the IRR
function.
 An approximate relationship may also be used:
e
after-tax ROR
Tax ROR =
1-T
Before
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-24 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

25. Example:
A company has spent $50,000 for a 5-year-life machine that has a
projected $20,000 annual CFBT and annual depreciation of
$10,000. The company has a Te of 40%. Determine:
 Exact Before-Tax ROR and After-Tax ROR.
 Approximate Before-Tax ROR
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-25 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved

26. Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012
© 2012 by McGraw-Hill, New York, N.Y All Rights Reserved
17-26
After-tax and Before-tax Rates of return:
YEAR CFBT Depreciation TI Taxes CFAT
0 -50000 -50000
1 20000 10000 10000 4000 16000
2 20000 10000 10000 4000 16000
3 20000 10000 10000 4000 16000
4 20000 10000 10000 4000 16000
5 20000 10000 10000 4000 16000
ROR 28.65% 18.03%
Before-Tax ROR After-Tax ROR
Approximate Before-Tax ROR = After-Tax ROR / ( 1 - Te)
Equal 0.1803 / (1 - 0.4) = 0.3005 or 30.05%

27. Cash flows are important for determining
project profitability
 Cash Flow analysis is vital in determining project profitability.
This is particularly true when using annual CFAT values.
 Projects are judged based on PW or AW of their annual CFAT.
Calculated IRR or DCFRR (discounted cash flow rate of return)
are often used as well.
 Another useful criterion for judging profitability is known as the
economic value added (EVA).
 EVA is the increase in NPAT achieved from a ROR above the
MARR. EVA is higher for higher delta between ROR and MARR.
Slide Sets to accompany Blank & Tarquin, Engineering
Economy, 7th Edition, 2012 17-27 © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved