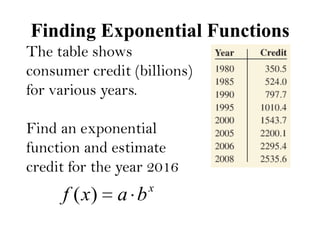
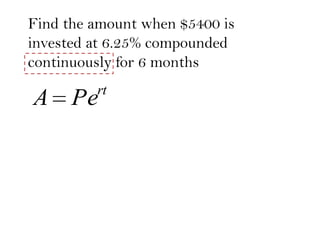The document contains an agenda for a class that includes attendance, sections on exponential applications and banking, and a quiz on Friday. It then provides examples and explanations of compound interest calculations using exponential functions, including continuously compounded interest. It concludes with examples of finding exponential functions from initial values and data points.

1. Today’s Agenda
 Attendance
/ Announcements
 Sections 4.1b / 4.2
 Quiz Friday

2. More Exponential Applications
Banking – Compounded Interest
Situation: An amount (“Principal”) is deposited
into an account. An interest rate (usually growth)
is applied to the amount in the bank at specific
times throughout the year. The amount in the
bank at any time can be found using….

3. Amount of
money in
bank
(balance)
t, Number of
years money left
in account
r, Interest rate
(as a decimal!)
r
A P1
n
nt
P, amount initially
n, Number of times
deposited, principal
compounded PER
YEAR

4. Find the amount when $9000 is invested at 5.4%
compounded monthly for 6 years.

5. A total of $12,000 is invested at an interest rate of
3%. Find the balance after 4 years if the interest is
compounded quarterly.

6. Example: You deposit $5,000 into an account with a 6.5%
interest rate. Find the amount in the account after 10 years.

7. What happens if interest is
compounded more than
daily, hourly, every minute!?
Continuously!
r
A P1
n
nt
rt
A Pe
What is e ?

8. 1
e lim 1
x
x
x
So, it’s just a
constant number
between 2 and 3!
2.718

9. Find the amount when $5400 is
invested at 6.25% compounded
continuously for 6 months
rt
A Pe

10. Finding Exponential Functions
Need initial value (0, …), and another
data point (x, y).
Substitute into exponential function:
f ( x)
a b
x
Solve for the growth/decay rate.
Then rewrite exp. function.
(similar to what we’ve done before)

11. Finding Exponential Functions
Find the exponential function of the
form that passes through the points
(0,100) and (4, 1600)
f ( x)
a b
x

12. Finding Exponential Functions
A population of bacteria grew from 24
to 615 over the course of 5 hours, find
an exponential function to model this
growth f ( x) a b x

13. Finding Exponential Functions
The table shows
consumer credit (billions)
for various years.
Find an exponential
function and estimate
credit for the year 2016
f ( x)
a b
x

14. Classwork
• Worksheet