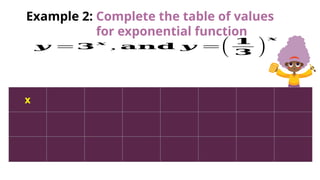
The document provides an educational module on solving exponential equations, defining exponential functions, and illustrating real-life applications such as population growth and compound interest. It includes exercises and activities for students to practice simplifications, create exponential models, and solve related problems. An assessment component is also included to evaluate understanding of the material.