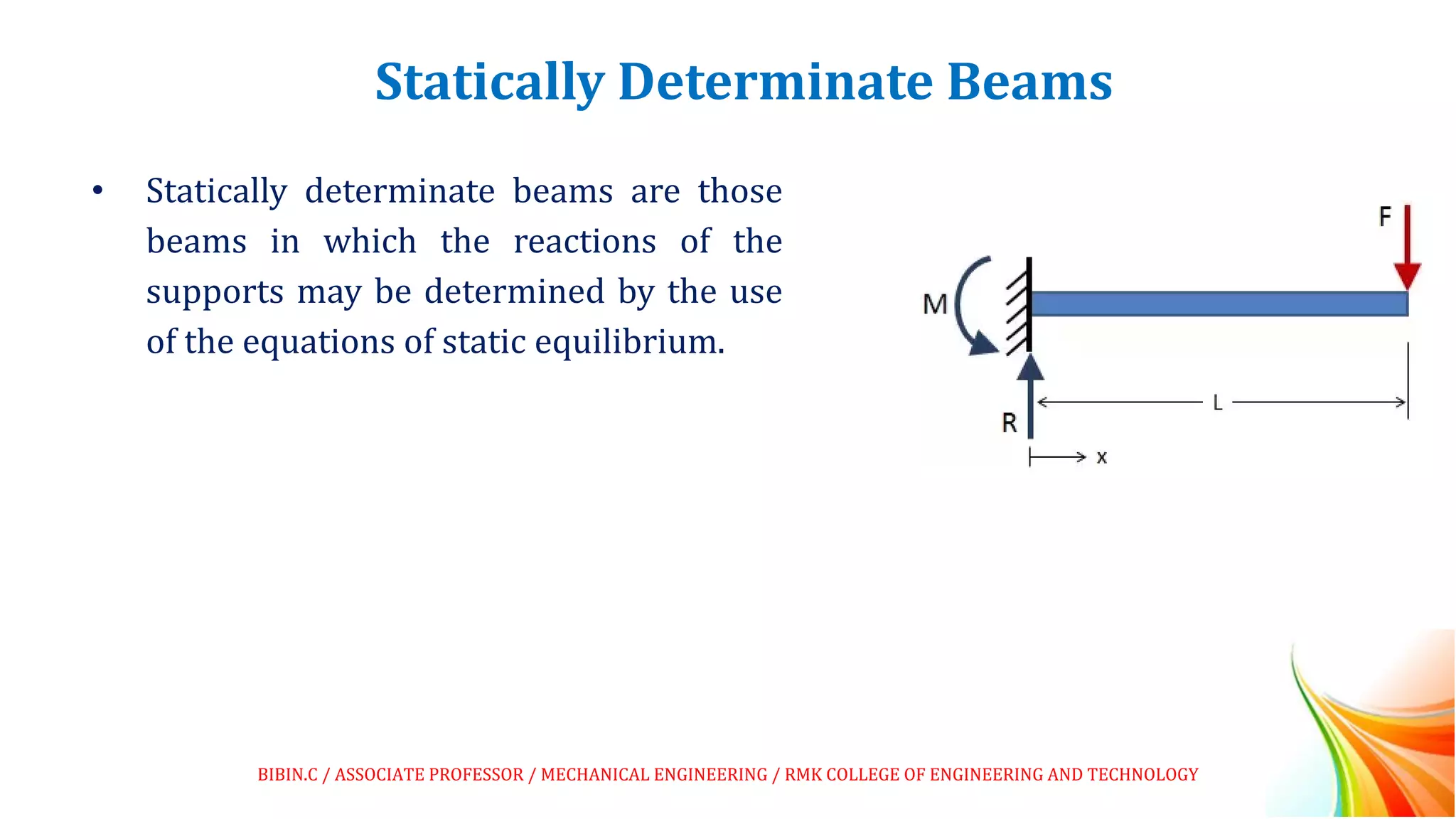
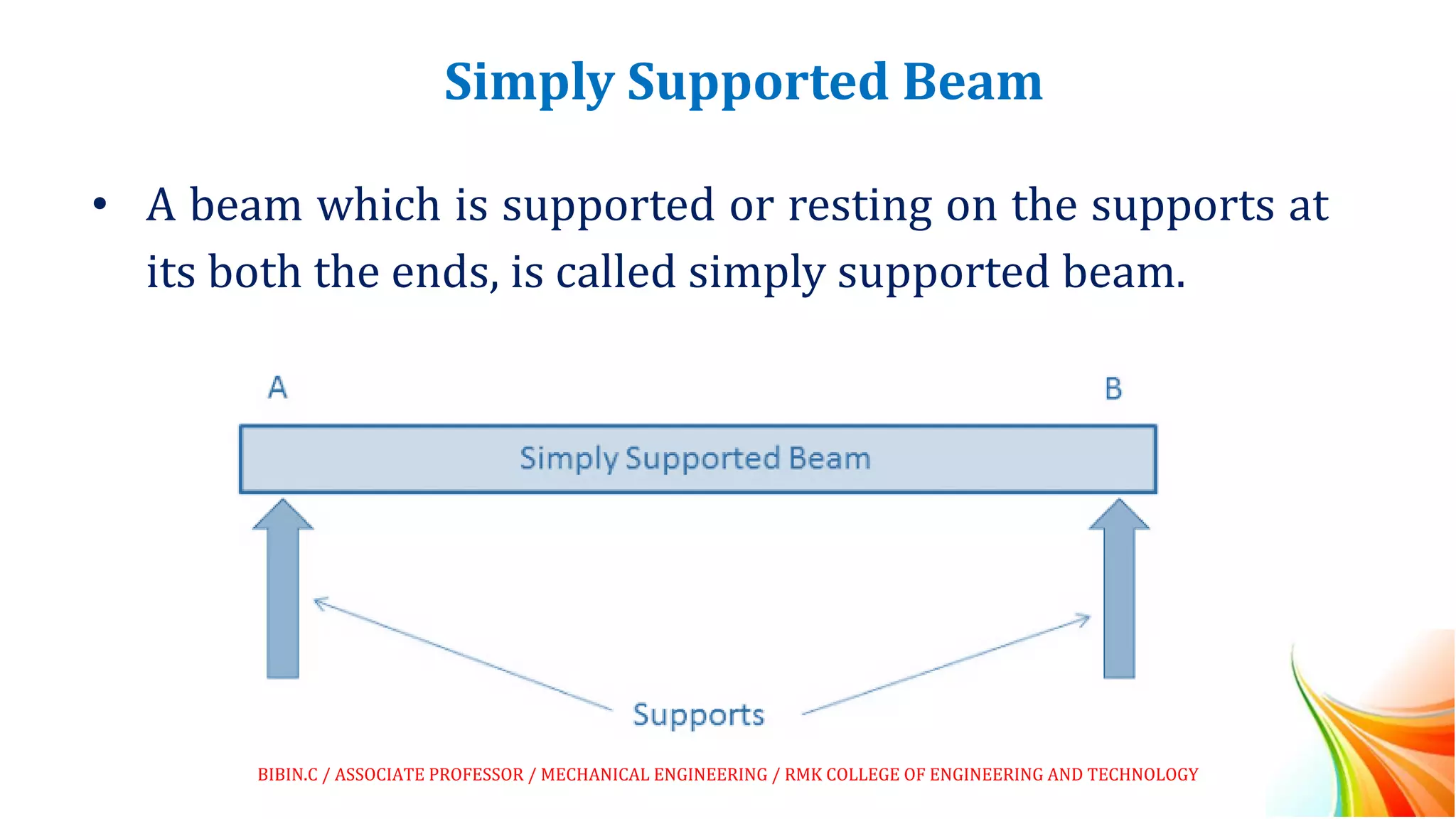
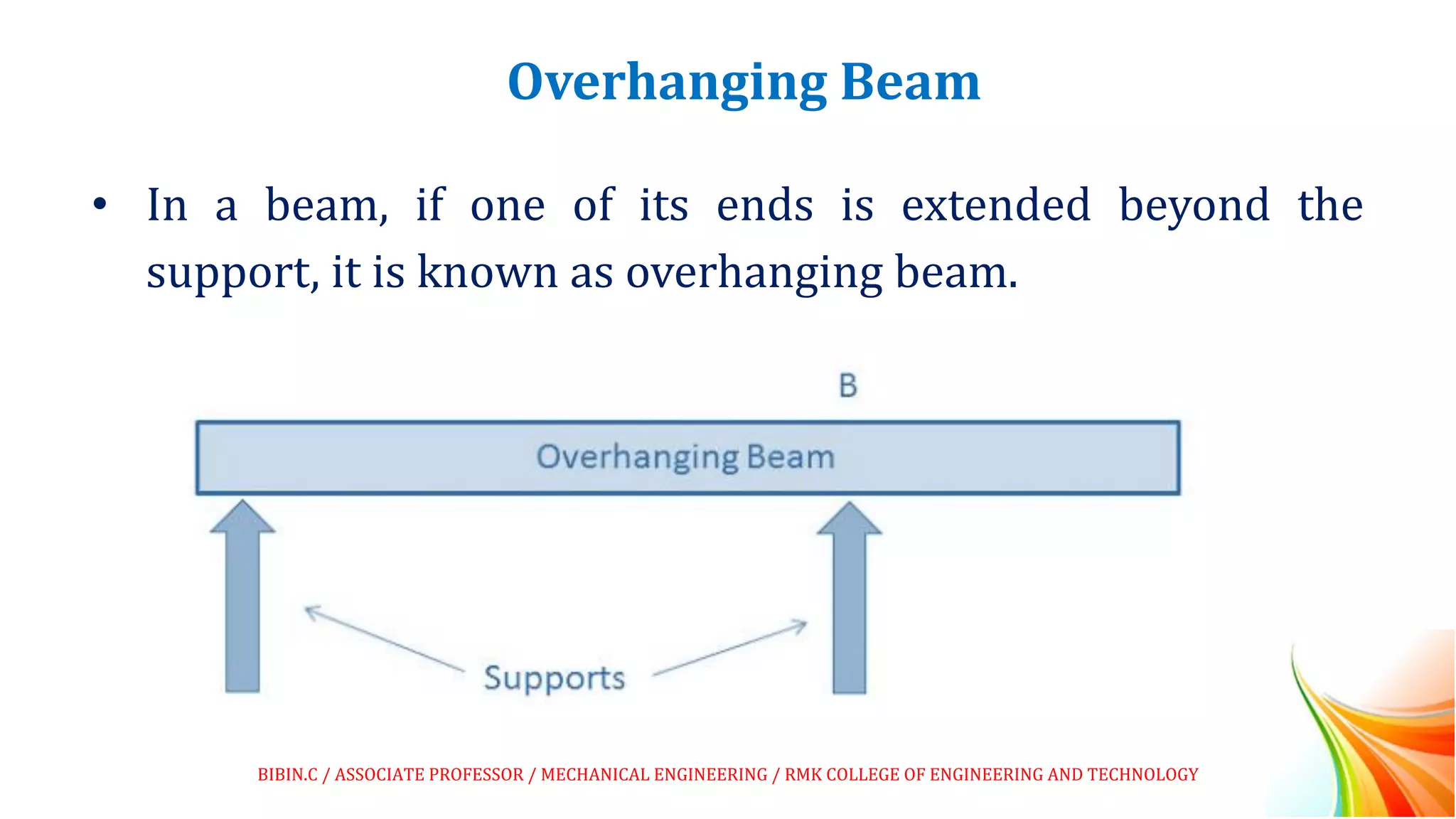
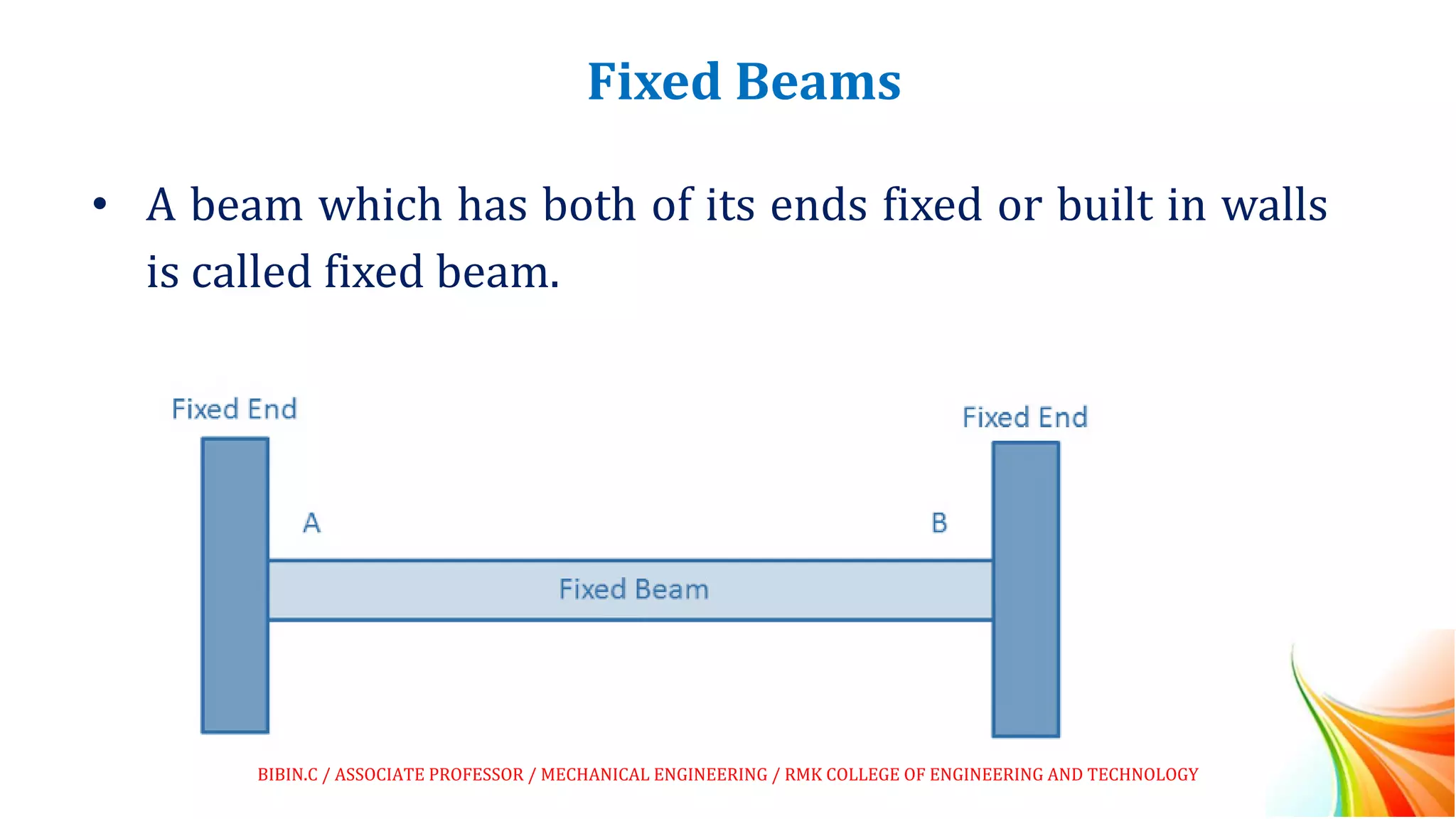
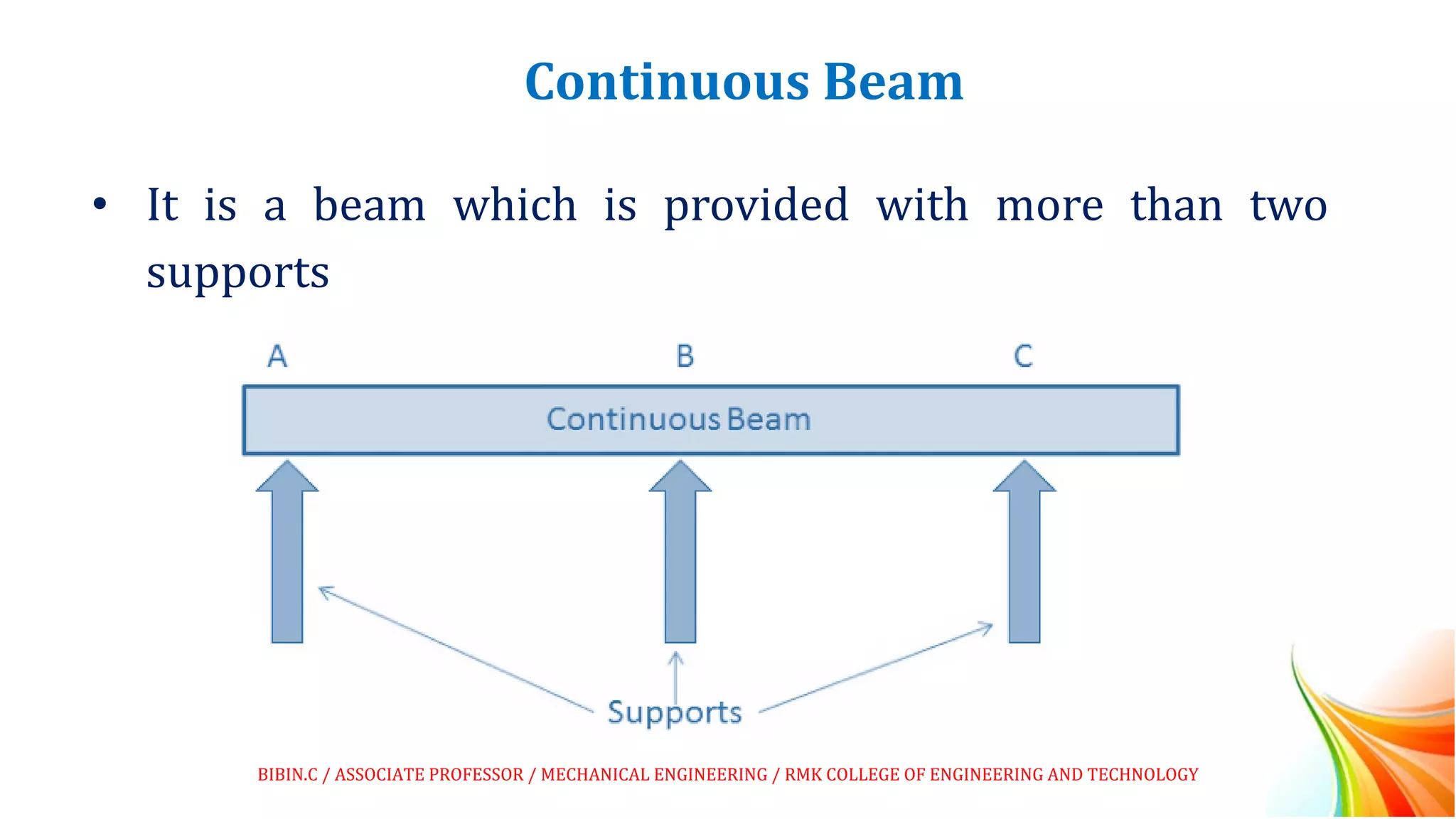
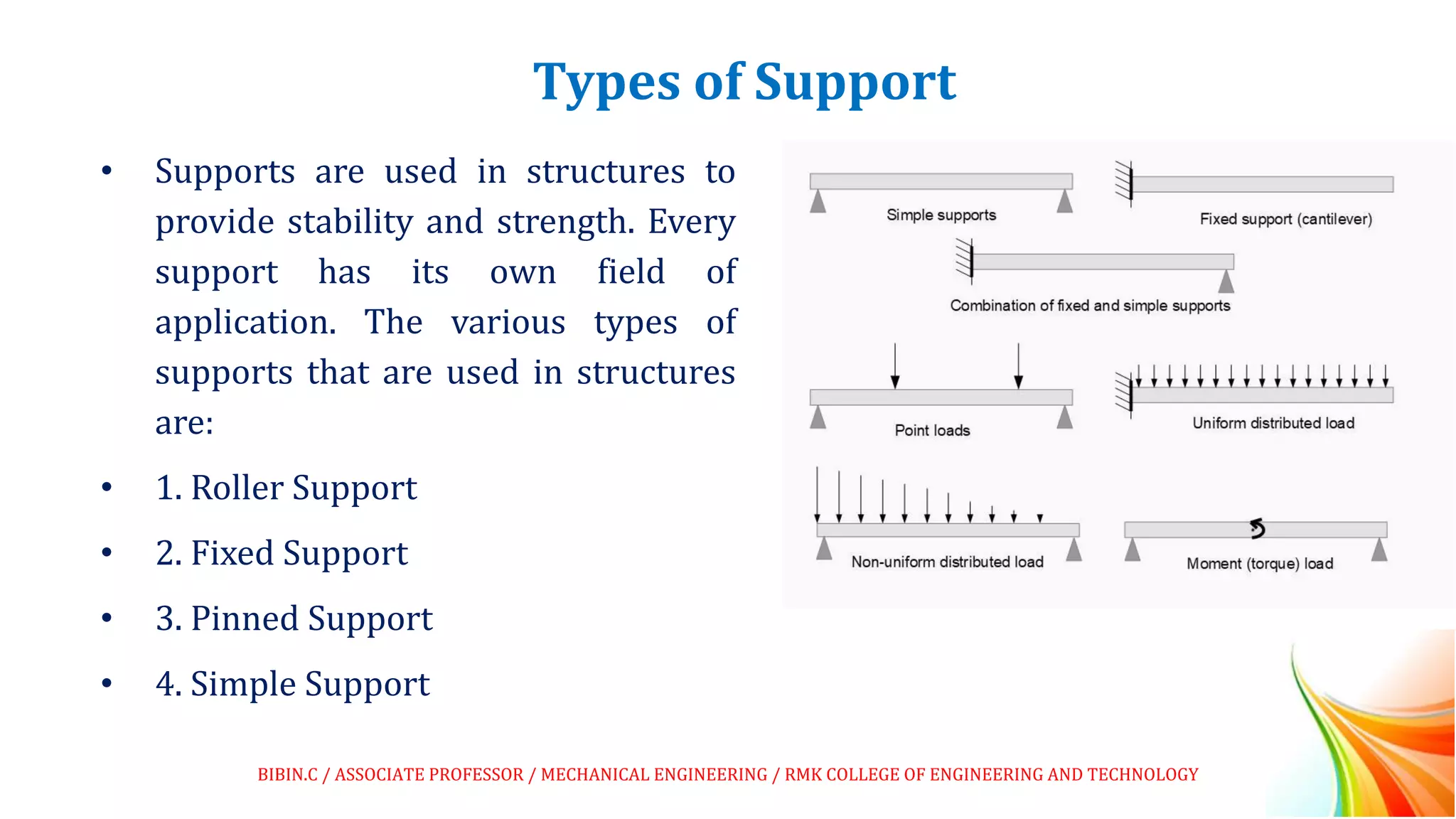
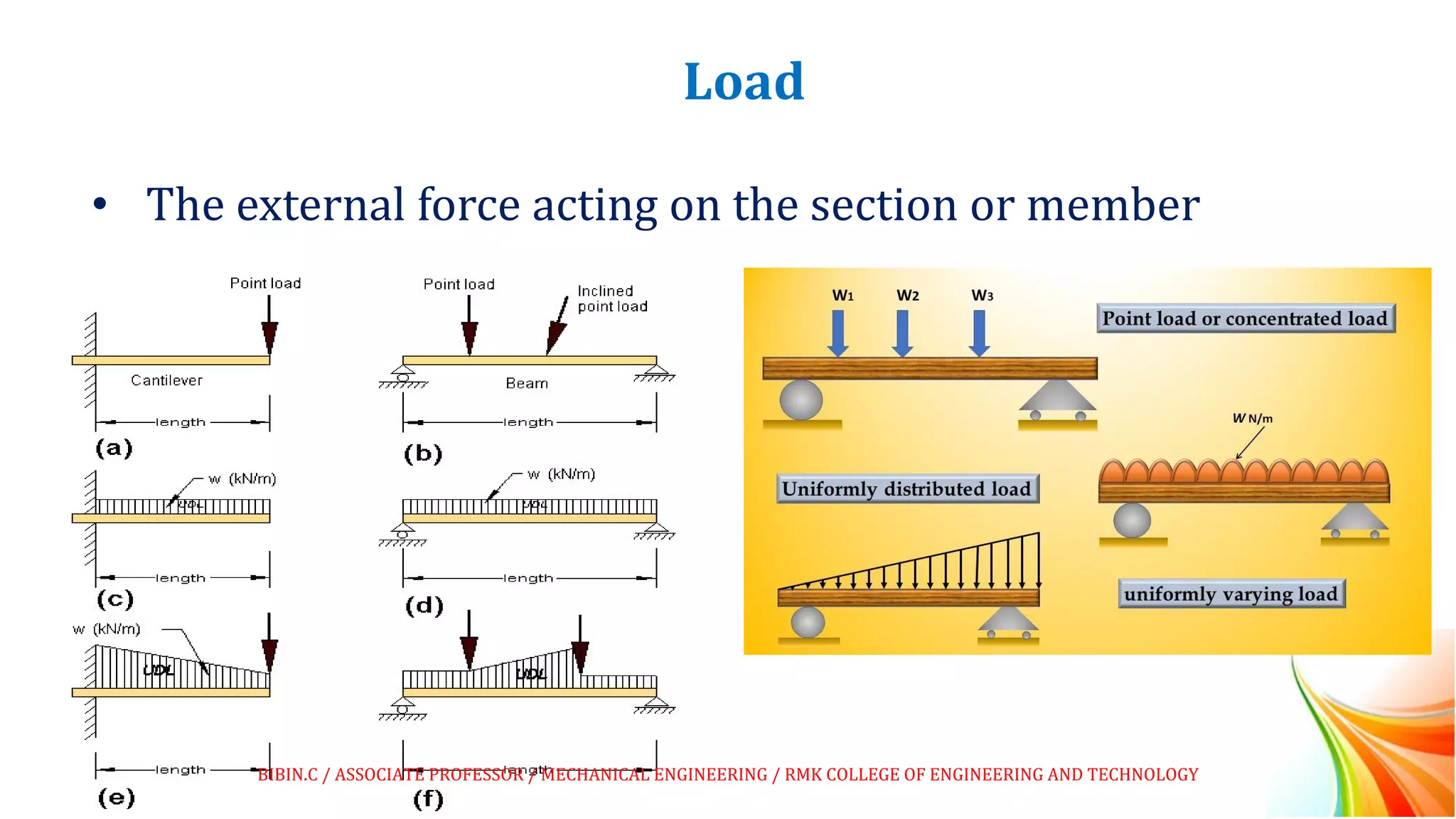
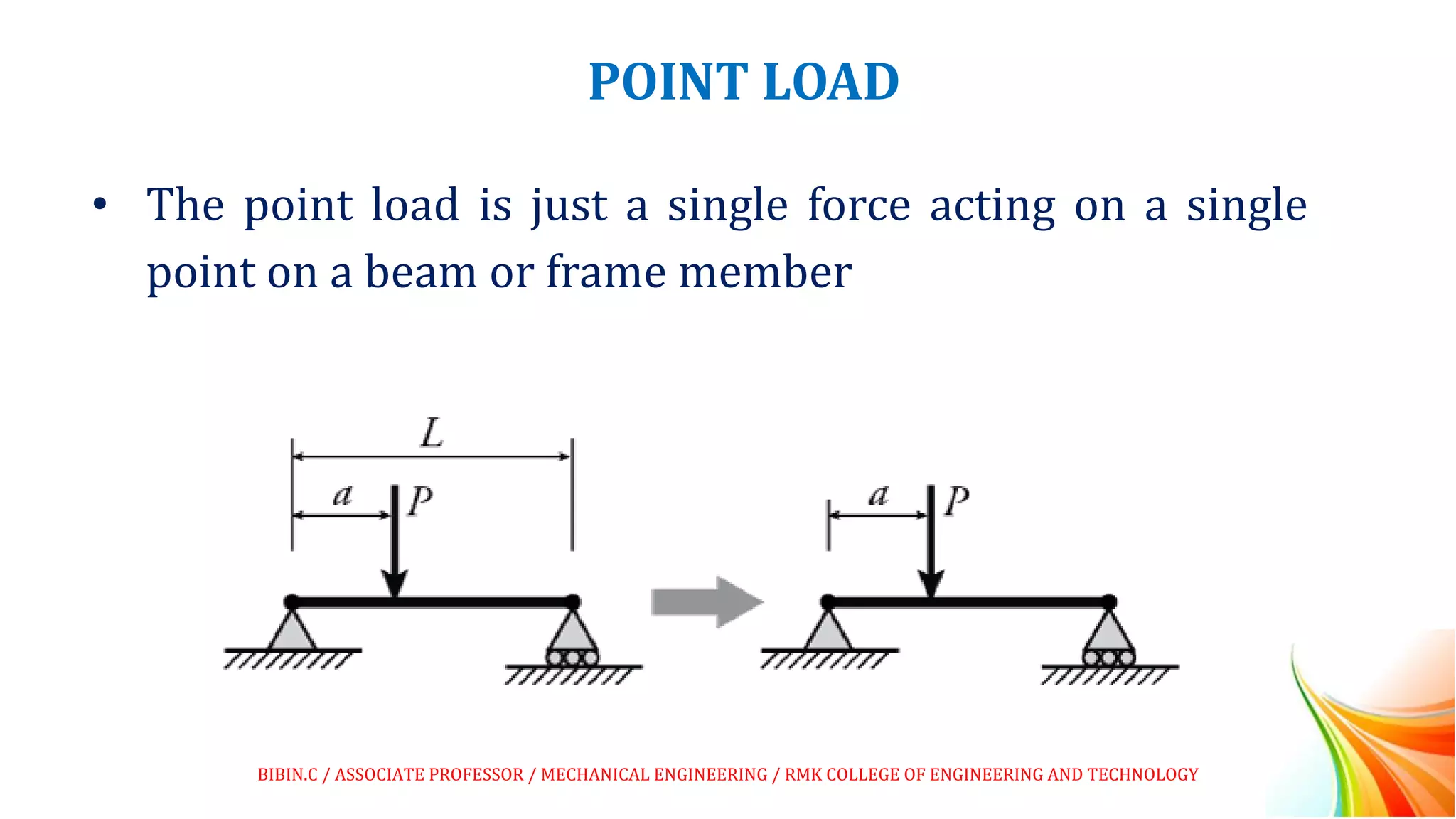
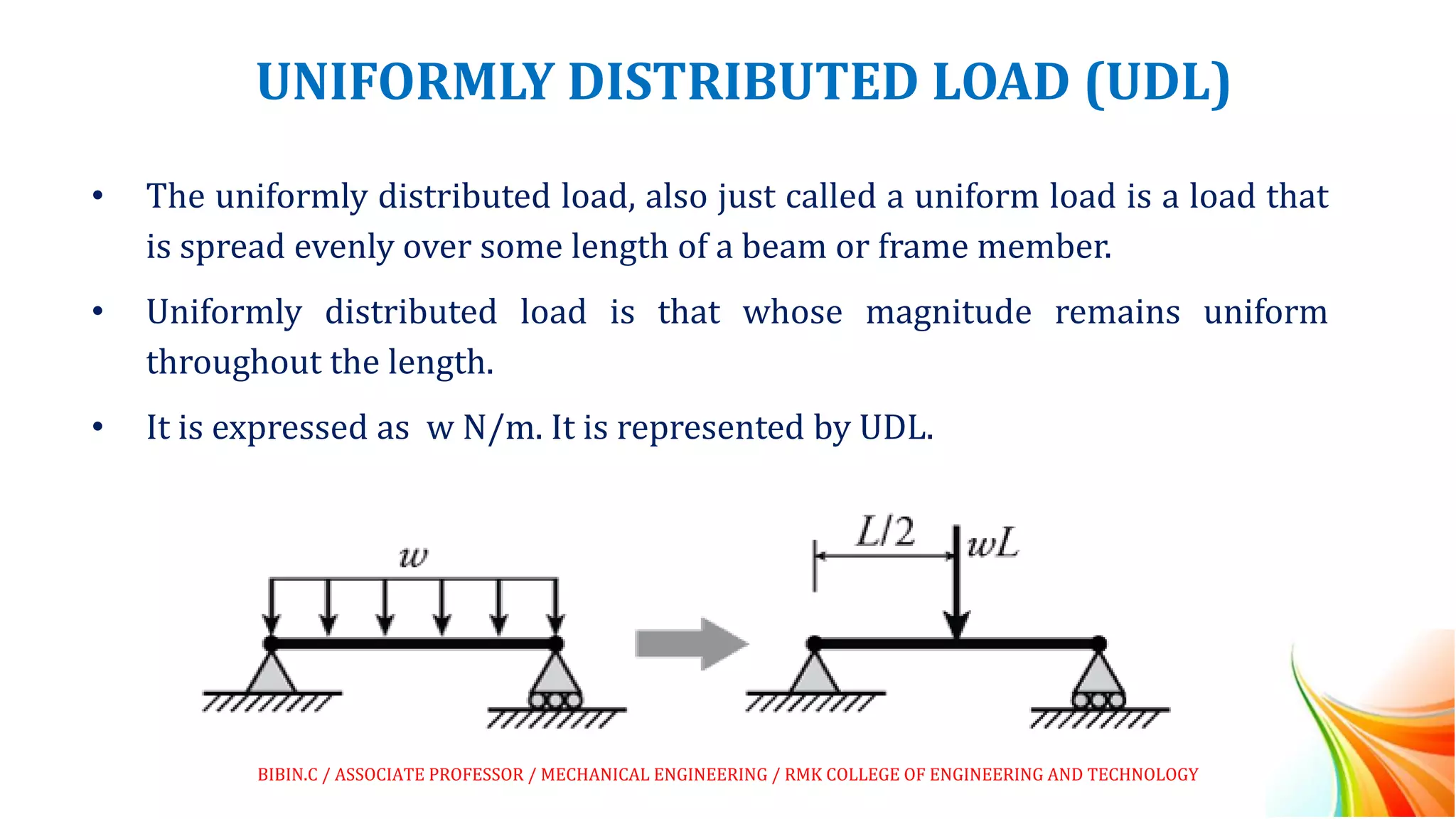
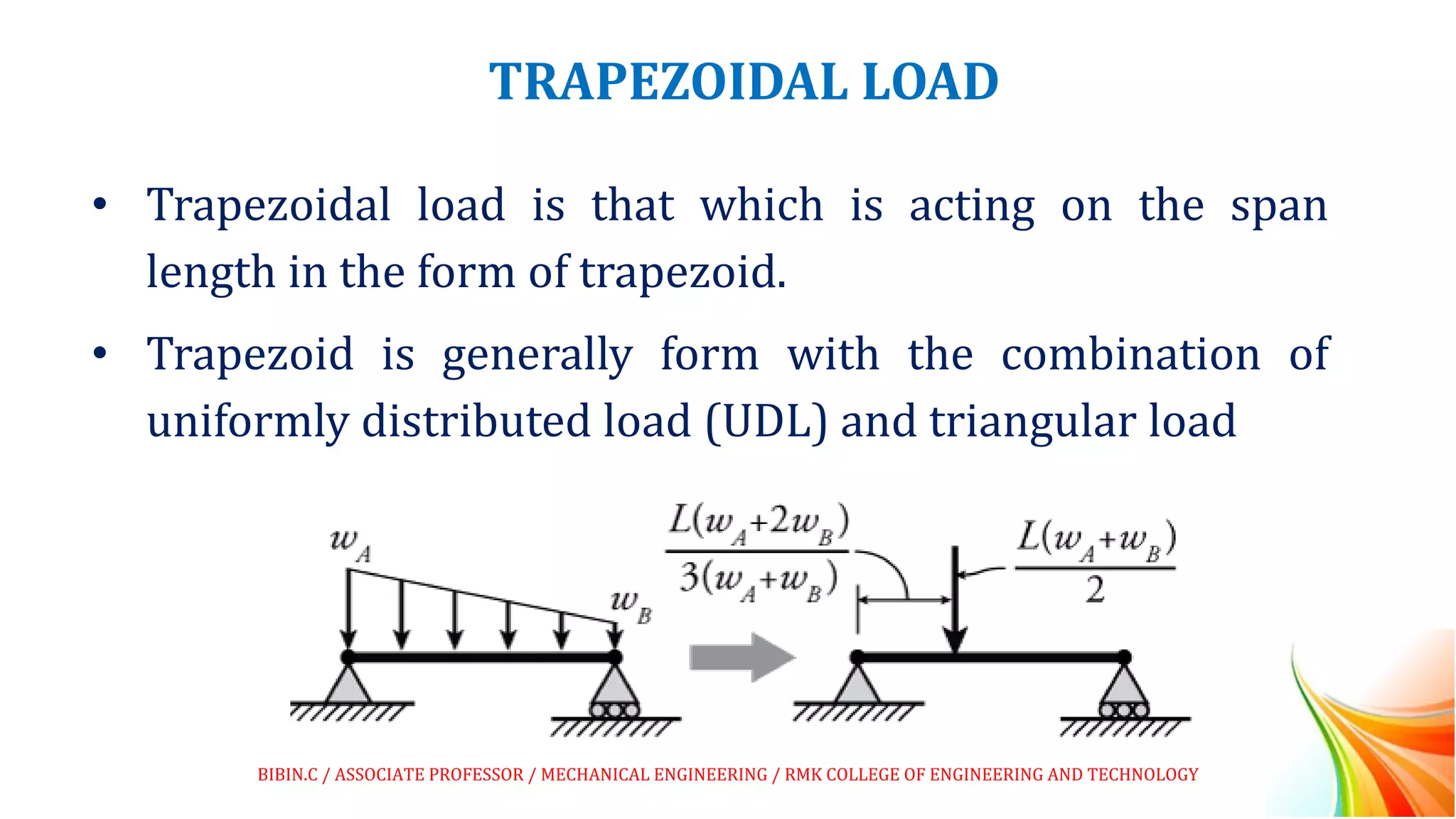
This document discusses beams and beam loading. It defines beams and describes different types of beams including cantilever, simply supported, overhanging, fixed, continuous, and propped cantilever beams. It also discusses beam supports, describing roller, pinned, fixed, and simple supports. Additionally, it covers loads on beams, identifying point loads, distributed loads, and coupled loads. Structures and beams can be either statically determinate or statically indeterminate, and the differences between these two types are explained.

1. BIBIN CHIDAMBARANATHAN
TRANSVERSE
LOADING ON BEAMS
AND STRESSES IN
BEAM
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

2. Structures & Classifications
• Structures are a group of members, such as beams, columns, slabs,
foundations, girders, and trusses, that work as a unit to fulfill a
purpose.
• Structures as classified into either being statically determinate or
statically indeterminate.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

3. Statically determinate structures
• Determinate structures are analysed just by the use of basic
equilibrium equations.
• By this analysis, the unknown reactions are found for the
further determination of stresses.
• Example of determinate structures are: simply supported
beams, cantilever beams, single and double overhanging
beams, three hinged arches, etc.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

4. Redundant or Statically indeterminate structures
• Redundant or indeterminate structures are not capable of being
analysed by mere use of basic equilibrium equations.
• Along with the basic equilibrium equations, some extra conditions
are required to be used like compatibility conditions of
deformations etc to get the unknown reactions for drawing bending
moment and shear force diagrams.
• Examples of indeterminate structures are: fixed beams, continuous
beams, fixed arches, two hinged arches, portals, multistoried
frames, etc.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

5. Difference Between Determinate and Indeterminate Structures
S. No. Determinate Structures Indeterminate Structures
1 Equilibrium conditions are fully adequate to analyze
the structure.
Conditions of equilibrium are not adequate to fully
analyze the structure.
2 Bending moment or shear force at any section is
independent of the material property of the
structure.
Bending moment or shear force at any section depends
upon the material property.
3 The bending moment or shear force at any section is
independent of the cross-section or moment of
inertia.
The bending moment or shear force at any section
depends upon the cross-section or moment of inertia.
4 Temperature variations do not cause stresses. Temperature variations cause stresses.
5 No stresses are caused due to lack of fit. Stresses are caused due to lack of fit.
6 Extra conditions like compatibility of displacements
are not required to analyze the structure.
Extra conditions like compatibility of displacements are
required to analyze the structure along with the
equilibrium equations.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

6. Beam
• The beam is defined as the structural
member which is used to bear different
loads.
• It resists the vertical loads, shear forces
and bending moments.
• A beam is a bar subject to forces or
couples that lie in a plane containing
the longitudinal section of the bar.
• According to determinacy, a beam may
be determinate or indeterminate.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

7. Statically Determinate Beams
• Statically determinate beams are those
beams in which the reactions of the
supports may be determined by the use
of the equations of static equilibrium.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

8. Statically Indeterminate Beams
• If the number of reactions exerted upon a beam exceeds the number of equations in
static equilibrium, the beam is said to be statically indeterminate.
• In order to solve the reactions of the beam, the static equations must be
supplemented by equations based upon the elastic deformations of the beam.
• The degree of indeterminacy is taken as the difference between the number of
reactions to the number of equations in static equilibrium that can be applied.
• In the case of the propped beam shown, there are three reactions RA, RB, and MA
and only two equations (ΣM = 0 and ΣFv = 0) can be applied, thus the beam is
indeterminate to the first degree (3 - 2 = 1).
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

9. Types of Beams
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

10. Cantilever Beam
• A cantilever beam is a beam that is fixed from one end
and free at the other end.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

11. Simply Supported Beam
• A beam which is supported or resting on the supports at
its both the ends, is called simply supported beam.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

12. Overhanging Beam
• In a beam, if one of its ends is extended beyond the
support, it is known as overhanging beam.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

13. Fixed Beams
• A beam which has both of its ends fixed or built in walls
is called fixed beam.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

14. Continuous Beam
• It is a beam which is provided with more than two
supports
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

15. Propped Cantilever Beam
• In propped cantilever beam, the free end of the
cantilever beam is place on a roller support
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

16. Structural support
• A structural support is a part of a building or structure that
provides the necessary stiffness and strength in order to resist
the internal forces (vertical forces of gravity and lateral forces
due to wind and earthquakes) and guide them safely to the
ground.
• External loads (actions of other bodies) that act on buildings
cause internal forces (forces and couples by the rest of the
structure) in building support structures.
• Supports can be either at the end or at any intermediate point
along a structural member.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

17. Types of Support
• Supports are used in structures to
provide stability and strength. Every
support has its own field of
application. The various types of
supports that are used in structures
are:
• 1. Roller Support
• 2. Fixed Support
• 3. Pinned Support
• 4. Simple Support
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

18. Roller Support
• It is a support which is free to rotate and translate along the surface on which
they rest.
• The surface on which the roller supports are installed may be horizontal, vertical,
and inclined to any angle.
• The roller supports has only one reaction, this reaction acts perpendicular to the
surface and away from it.
• The roller supports are unable to resists the lateral loads (the lateral loads are
the live loads whose main components are horizontal forces).
• They resist only vertical loads.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

19. Pinned Support (hinge support)
• It is a types of support which resists the horizontal and vertical loads but is unable to resists
the moment.
• The pinned support has two support reactions and these are vertical and horizontal reactions.
• It allows the structural member to rotate but does not allow translating in any direction.
• The pinned support allows the rotation only in one direction and resists the rotation in any
other direction.
• The best example is the doors and windows of our houses and our knee joint. Here the
rotation happens in one direction but the translation motion is restricted.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

20. Fixed Support (rigid support)
• It is a support which is capable of resisting all types of loads i.e. horizontal, vertical
as well as moments.
• The fixed support does not allow the rotation and translation motion to the
structural members.
• A flagpole fixed in the concrete base is the best example of fixed support.
• The other examples of the fixed support are electric pole in the streets, a bracket on
the wall, and all the riveted and welded joints in the steel etc.
• It provides the greater stability to the structure as compared with all other
supports.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

21. Simple Support
• The simple support is used where the structural member has to rest on the
external structure.
• These types of support are not used widely in daily life. It is similar to the
roller support.
• The simple supports resist only vertical forces or loads but not horizontal
forces.
• A pan of wood resting on two concrete blocks is the best example of a simple
support.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

22. Summary of Different Types of Support
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

23. Load
• The external force acting on the section or member
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

24. Types of Load
• There are three types of load. These are;
• Point load that is also called as concentrated load.
• Distributed load
• Coupled load
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

25. POINT LOAD
• The point load is just a single force acting on a single
point on a beam or frame member
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

26. DISTRIBUTED LOAD
• Distributed load is that acts over a considerable length or “over a
length which is measurable.
• Distributed load is measured as per unit length.
TYPES OF DISTRIBUTED LOAD
• Uniformly Distributed load (UDL)
• Uniformly Varying load (Non-uniformly distributed load).
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

27. UNIFORMLY DISTRIBUTED LOAD (UDL)
• The uniformly distributed load, also just called a uniform load is a load that
is spread evenly over some length of a beam or frame member.
• Uniformly distributed load is that whose magnitude remains uniform
throughout the length.
• It is expressed as w N/m. It is represented by UDL.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

28. Uniformly varying load (triangular load)
• The load which is spread on the section of member such that rate
of loading varies from the point to point in which load at one
section is zero and increase uniformly to the other end.
• For solving the problems the total load is equal to the area of
triangular and this total load is assumed to be acting at centre of
gravity of the triangle i.e. at a distance of 1/3 rd of total length
from the left side.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

29. TRAPEZOIDAL LOAD
• Trapezoidal load is that which is acting on the span
length in the form of trapezoid.
• Trapezoid is generally form with the combination of
uniformly distributed load (UDL) and triangular load
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

30. COUPLED LOAD
• Coupled load is that in which two equal and opposite forces acts on the
same span.
• The lines of action of both the forces are parallel to each other but opposite
in directions. This type of loading creates a couple load.
• Coupled load try to rotate the span in case one load is slightly more than the
2nd load. If force on one end of beam acts upward then same force will acts
downwards on the opposite end of beam.
• Coupled load is expressed as N.m
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

31. Shear Force
• The shear force at any point along a loaded beam may be defined as the
algebraic sum of all vertical forces acting on either side of the point on the
beam.
• The net effect of the shear force is to shear off the beam along with the point at
which it is acting.
• Shear force is taken +𝑖𝑣𝑒 if it produces a clockwise moment and it is taken
− 𝑖𝑣𝑒 when it produces an anticlockwise moment.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

32. Bending Moment
• Bending moment at any point along a loaded beam may be defined as the sum
of the moments due to all vertical forces acting on either side of the point on
the beam.
• The bending moment tries to bend the beam.
• Clockwise moments due to loads acting to the left of the section are assumed
to be +𝑖𝑣𝑒, while anticlockwise moments are taken −𝑖𝑣𝑒.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

33. Sign Convention Used For Shear Force
• Force acting in the right-hand side of the section in the upward direction is
taken −𝑖𝑣𝑒 and force in the right-hand side of the section acting in the
downward direction are taken as +𝑖𝑣𝑒.
• Similarly, a force in the left hand side of the section is taken +𝑖𝑣𝑒 if it is acting
in an upward direction and it is taken as negative if it is acting in a downward
direction.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

34. Sign Convention Used For Bending Moment
• First of all remove all the loads and reaction from any one side of the section.
• Now introduce each load and reaction one at a time and find its effect at the
section.
• A bending moment causes concavity upwards is taken +𝑖𝑣𝑒 and called a
sagging bending moment.
• A bending moment which is causing convexity upwards is taken −𝑖𝑣𝑒 and
called as hogging bending moment.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

35. Shear Force Diagrams
• A shear force diagram which shows the shear force at every
section of the beam due to transverse loading on it.
• Its baseline is equal to the span of the beam, drawn on a suitable
scale.
• For point loads S.F. diagram has a straight horizontal line,
• for UDL ( Uniformly Distributed Load), It has straight inclined lines,
and
• for uniformly varying loads it has a parabolic curve.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

36. Bending Moment Diagrams
• A bending moment diagram is a diagram which shows the bending
moment at every section of the beam due to transverse loading on
it.
• in case of a simply supported beam bending moment is zero at the
ends, and for a cantilever, it is zero at the free end.
• For point loads, B.M. diagram has straight inclined lines, for UDL, it
has a parabolic curve and for the uniformly varying load, it has a
cubic curve.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

37. Important Points Must Be Kept In Mind While Drawing The
Shear Force And Bending Moment Diagram
• First of all, consider either the left or the right-hand side of the section.
• Add the forces (Including Reactions) normal to the beam on one of the side, if the
right-hand side of the section is chosen, a force acting downwards is taken +𝑖𝑣𝑒 while
a force acting upwards is −𝑖𝑣𝑒.
• The +𝑖𝑣𝑒 values of shear force and bending moment are plotted above the baseline,
and −𝑖𝑣𝑒 values below the baseline.
• The shear force diagram will decrease or increase suddenly shown by a vertical
straight line at a section when there is a vertical point load.
• The shear force between any two vertical loads will be constant and hence the shear
force diagram between two vertical loads will be horizontal.
• The bending moment at the two supports of a simply supported beam and also at the
free end of a cantilever will be zero.
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY

38. Thank You
BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY