Download as PDF, PPTX
Uploaded byBIBIN CHIDAMBARANATHAN
Lecture 12 som 10.03.2021
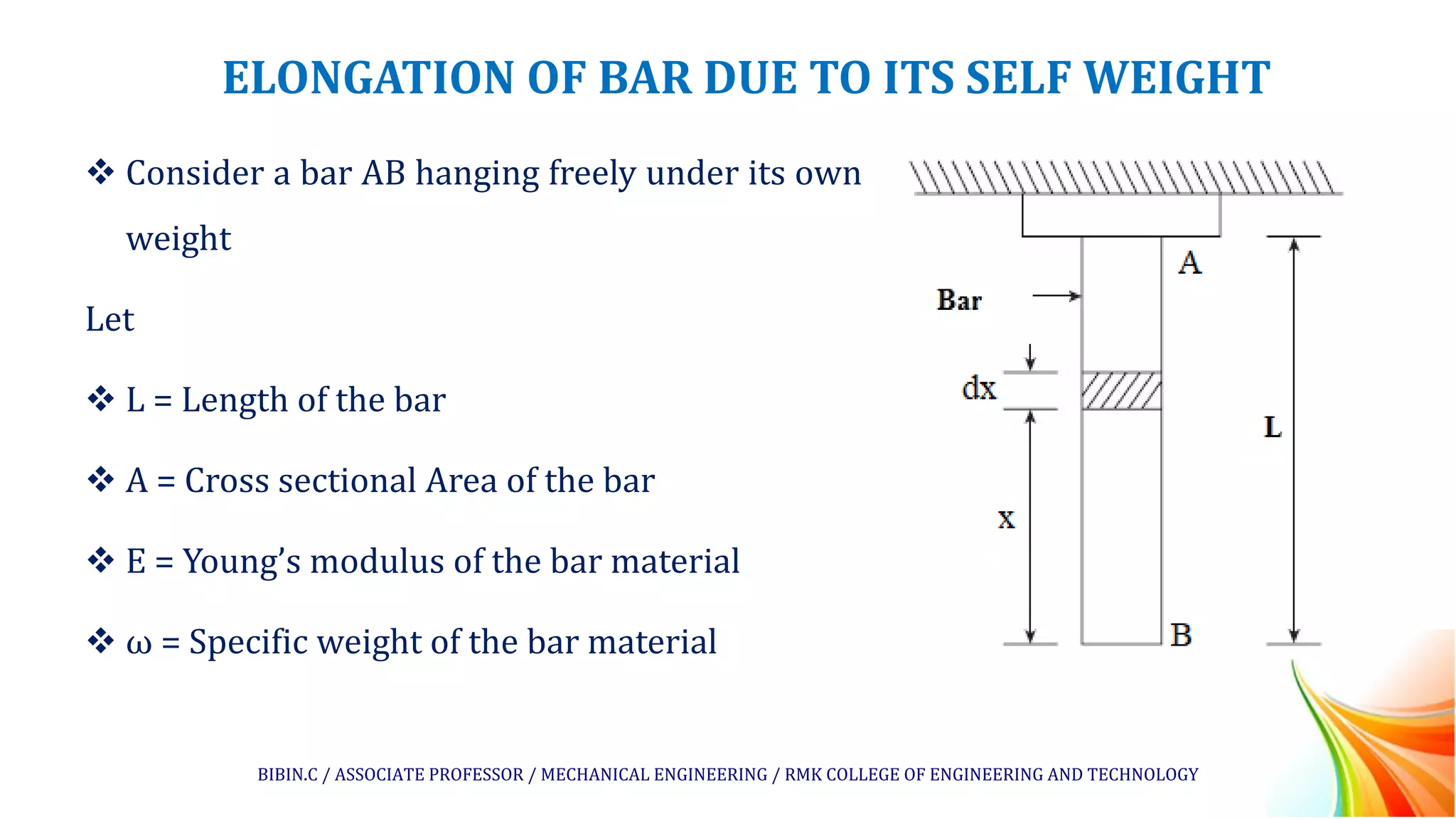
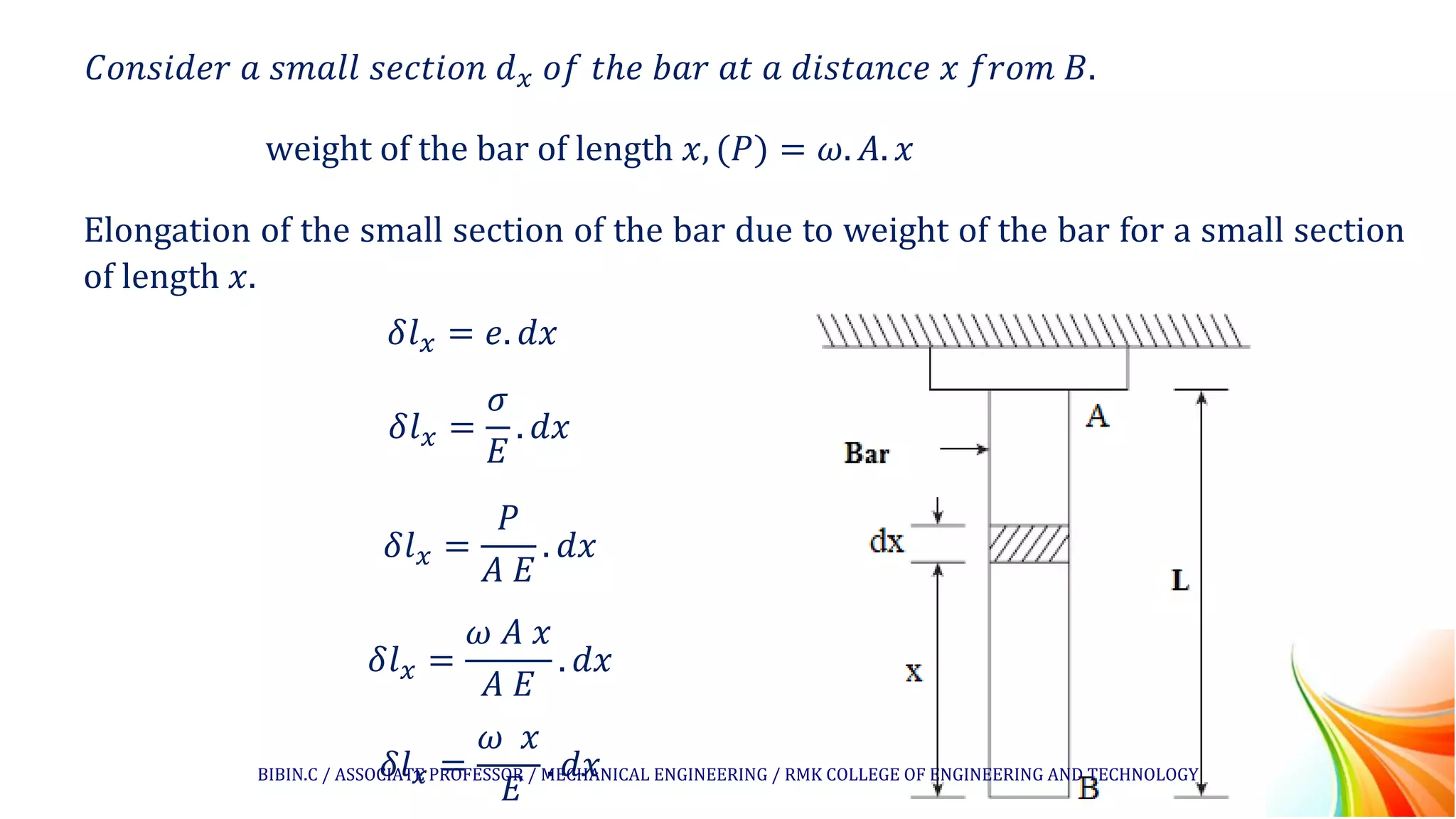
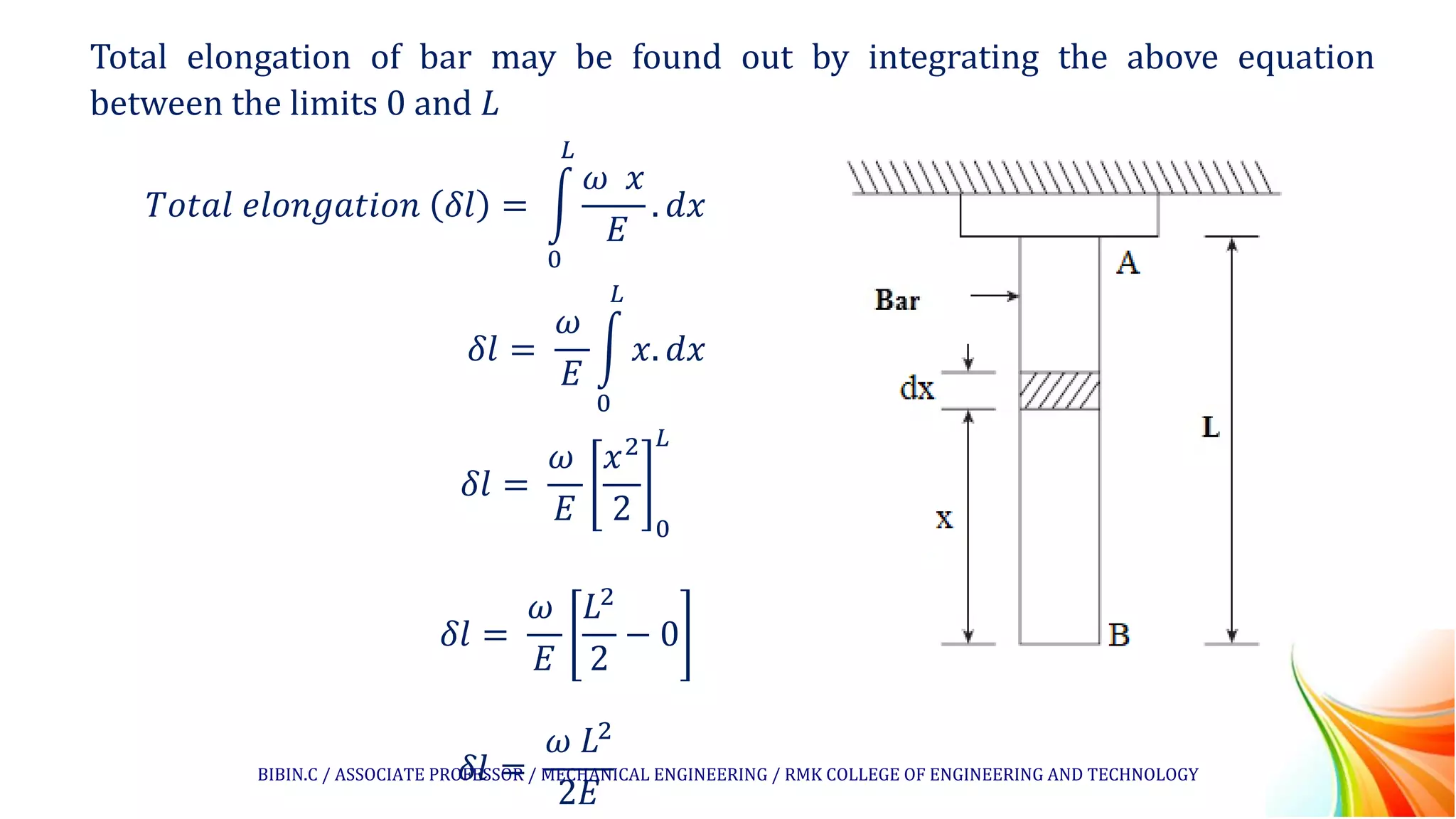
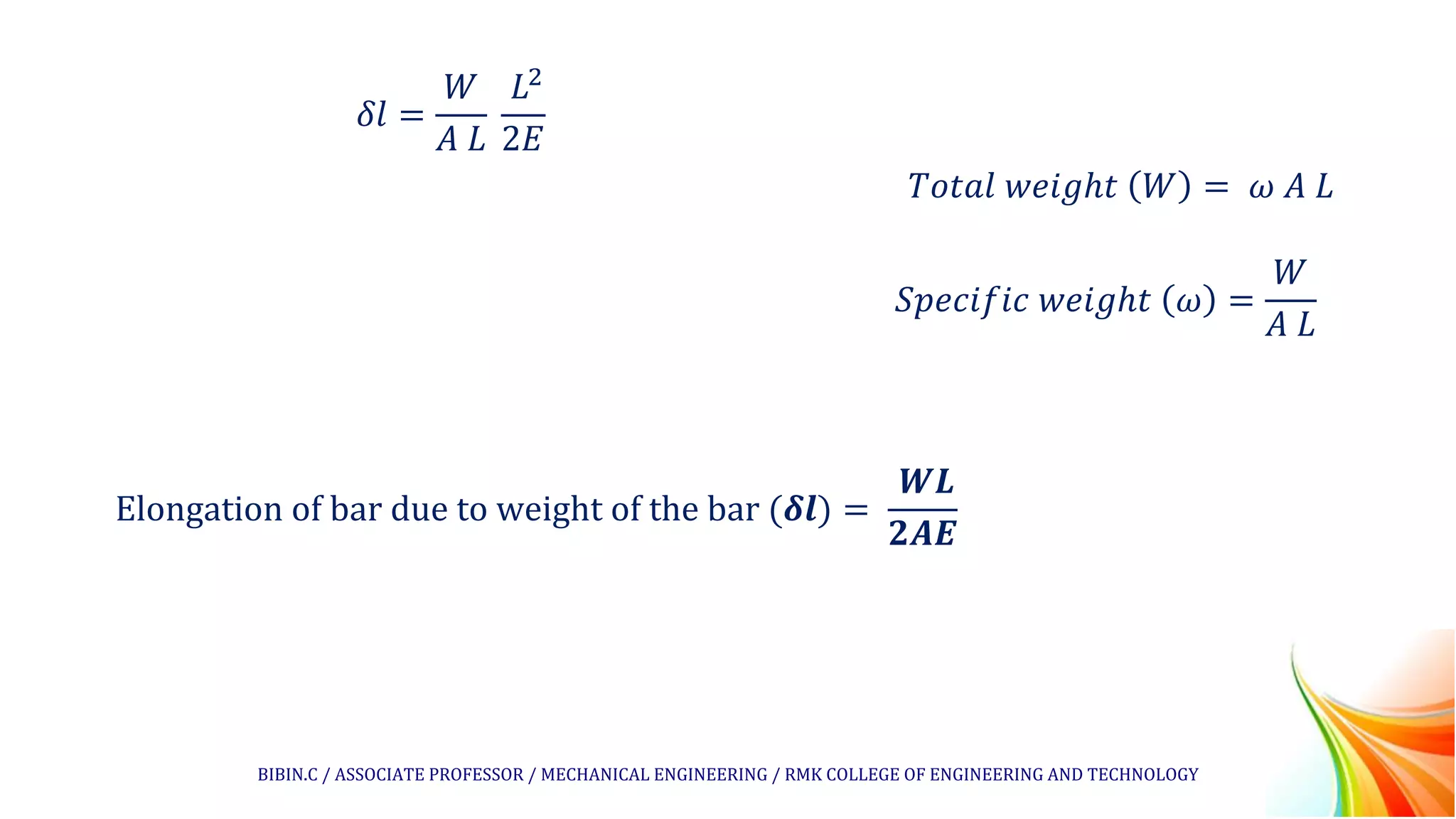
The document discusses the elongation of a bar hanging freely due to its own weight. It defines the key parameters that affect elongation such as the length, cross-sectional area, Young's modulus, and specific weight of the material. An equation is derived to calculate the total elongation of the bar by integrating the elongation of small sections over the length of the bar. Several example problems are then presented and solved using this equation to find the elongation of bars or wires under self-weight loading conditions.
More Related Content
Lecture 12 som 10.03.2021
- 1. BIBIN CHIDAMBARANATHAN ELONGATION OFBAR DUE TO ITS SELF WEIGHT BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY
- 2. ELONGATION OF BARDUE TO ITS SELF WEIGHT ❖ Consider a bar AB hanging freely under its own weight Let ❖ L = Length of the bar ❖ A = Cross sectional Area of the bar ❖ E = Young’s modulus of the bar material ❖ ω = Specific weight of the bar material BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY
- 3. 𝐶𝑜𝑛𝑠𝑖𝑑𝑒𝑟 𝑎 𝑠𝑚𝑎𝑙𝑙𝑠𝑒𝑐𝑡𝑖𝑜𝑛 𝑑𝑥 𝑜𝑓 𝑡ℎ𝑒 𝑏𝑎𝑟 𝑎𝑡 𝑎 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒 𝑥 𝑓𝑟𝑜𝑚 𝐵. weight of the bar of length 𝑥, (𝑃) = 𝜔. 𝐴. 𝑥 Elongation of the small section of the bar due to weight of the bar for a small section of length 𝑥. 𝛿𝑙𝑥 = 𝑒. 𝑑𝑥 𝛿𝑙𝑥 = 𝜎 𝐸 . 𝑑𝑥 𝛿𝑙𝑥 = 𝑃 𝐴 𝐸 . 𝑑𝑥 𝛿𝑙𝑥 = 𝜔 𝐴 𝑥 𝐴 𝐸 . 𝑑𝑥 𝛿𝑙𝑥 = 𝜔 𝑥 𝐸 . 𝑑𝑥 BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY
- 4. Total elongation ofbar may be found out by integrating the above equation between the limits 0 and 𝐿 𝑇𝑜𝑡𝑎𝑙 𝑒𝑙𝑜𝑛𝑔𝑎𝑡𝑖𝑜𝑛 𝛿𝑙 = න 0 𝐿 𝜔 𝑥 𝐸 . 𝑑𝑥 𝛿𝑙 = 𝜔 𝐸 න 0 𝐿 𝑥. 𝑑𝑥 𝛿𝑙 = 𝜔 𝐸 𝑥2 2 0 𝐿 𝛿𝑙 = 𝜔 𝐸 𝐿2 2 − 0 𝛿𝑙 = 𝜔 𝐿2 2𝐸 BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY
- 5. 𝛿𝑙 = 𝑊 𝐴 𝐿 𝐿2 2𝐸 𝑇𝑜𝑡𝑎𝑙𝑤𝑒𝑖𝑔ℎ𝑡 𝑊 = 𝜔 𝐴 𝐿 𝑆𝑝𝑒𝑐𝑖𝑓𝑖𝑐 𝑤𝑒𝑖𝑔ℎ𝑡 𝜔 = 𝑊 𝐴 𝐿 Elongation of bar due to weight of the bar (𝜹𝒍) = 𝑾𝑳 𝟐𝑨𝑬 BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY
- 6. Problem 01 A copperalloy wire of 1.5 𝑚𝑚 diameter and 30 𝑚 long is hanging freely from a tower. What will be its elongation due to self-weight? Take specific weight of copper and its modulus of elasticity as 89.4 𝑘𝑁/𝑚3 and 90 𝐺𝑃𝑎 respectively. 𝑮𝒊𝒗𝒆𝒏 𝒅𝒂𝒕𝒂: 𝑻𝒐 𝒇𝒊𝒏𝒅: Elongation due to self weight (𝛿𝑙)=? 𝑑 = 1.5 𝑚𝑚 𝐿 = 30 𝑚 = 30 × 103 𝑚𝑚 𝜔 = 89.2 𝑘 Τ 𝑁 𝑚3 = 89.2 × 10−6 Τ 𝑁 𝑚 𝑚3 𝑀𝑜𝑑𝑢𝑙𝑢𝑠 𝑜𝑓 𝑒𝑙𝑎𝑠𝑡𝑖𝑐𝑖𝑡𝑦 𝐸 = 90 𝐺𝑃𝑎 = 90 × 103 Τ 𝑁 𝑚 𝑚2 BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY
- 7. 𝐸𝑙𝑜𝑛𝑔𝑎𝑡𝑖𝑜𝑛 𝑑𝑢𝑒 𝑡𝑜𝑠𝑒𝑙𝑓 𝑤𝑒𝑖𝑔ℎ𝑡 𝛿𝑙 = 𝜔 𝐿2 2𝐸 𝑭𝒐𝒓𝒎𝒖𝒍𝒂 ∶ 𝑺𝒐𝒍𝒖𝒕𝒊𝒐𝒏: 𝐸𝑙𝑜𝑛𝑔𝑎𝑡𝑖𝑜𝑛 𝑑𝑢𝑒 𝑡𝑜 𝑠𝑒𝑙𝑓 𝑤𝑒𝑖𝑔ℎ𝑡 𝛿𝑙 = 𝜔 𝐿2 2𝐸 𝛿𝑙 = 89.2 × 10−6 × 30 × 103 2 × 90 × 103 𝑬𝒍𝒐𝒏𝒈𝒂𝒕𝒊𝒐𝒏 𝒅𝒖𝒆 𝒕𝒐 𝒔𝒆𝒍𝒇 𝒘𝒆𝒊𝒈𝒉𝒕 𝜹𝒍 = 𝟎. 𝟒𝟓 𝒎𝒎 𝑑 = 1.5 𝑚𝑚 𝐿 = 30 𝑚 = 30 × 103 𝑚𝑚 𝜔 = 89.2 × 10−6 Τ 𝑁 𝑚 𝑚3 𝐸 = 90 × 103 Τ 𝑁 𝑚 𝑚2 𝛿𝑙 = 0.45 𝑚𝑚 BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY
- 8. Problem 01 An alloywire of 2 𝑚𝑚2 cross sectional area and 12 𝑁 weight hangs freely under its own weight. Find the maximum length of the wire, if its extension is not to exceed 0.6 𝑚𝑚. Take E for wire material as 150 𝐺𝑃𝑎. 𝑮𝒊𝒗𝒆𝒏 𝒅𝒂𝒕𝒂: 𝑻𝒐 𝒇𝒊𝒏𝒅: Maximum length of the wire (L)=? 𝐴 = 2 𝑚𝑚2 𝑊 = 12 𝑁 𝛿𝑙 = 0.6 𝑚𝑚 𝑀𝑜𝑑𝑢𝑙𝑢𝑠 𝑜𝑓 𝑒𝑙𝑎𝑠𝑡𝑖𝑐𝑖𝑡𝑦 𝐸 = 150 𝐺𝑃𝑎 = 150 × 103 Τ 𝑁 𝑚 𝑚2 BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY
- 9. 𝑭𝒐𝒓𝒎𝒖𝒍𝒂 ∶ 𝑺𝒐𝒍𝒖𝒕𝒊𝒐𝒏: 𝐸𝑙𝑜𝑛𝑔𝑎𝑡𝑖𝑜𝑛 𝑑𝑢𝑒𝑡𝑜 𝑠𝑒𝑙𝑓 𝑤𝑒𝑖𝑔ℎ𝑡 𝛿𝑙 = 𝑊𝐿 2𝐴𝐸 0.6 = 12 × 𝐿 2 × 2 × 150 × 103 𝑴𝒂𝒙𝒊𝒎𝒖𝒎 𝒍𝒆𝒏𝒈𝒕𝒉 𝒐𝒇 𝒕𝒉𝒆 𝒘𝒊𝒓𝒆 𝑳 = 𝟑𝟎𝟎𝟎𝟎 𝒎𝒎 = 𝟑𝟎 𝒎 𝐸𝑙𝑜𝑛𝑔𝑎𝑡𝑖𝑜𝑛 𝑑𝑢𝑒 𝑡𝑜 𝑠𝑒𝑙𝑓 𝑤𝑒𝑖𝑔ℎ𝑡 𝛿𝑙 = 𝑊𝐿 2𝐴𝐸 𝐴 = 2 𝑚𝑚2 𝑊 = 12 𝑁 𝛿𝑙 = 0.6 𝑚𝑚 𝐸 = 150 × 103 Τ 𝑁 𝑚 𝑚2 𝐿 = 30000 𝑚𝑚 BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY
- 10. Problem 01 A steelwire ABC 16 𝑚 long having cross sectional area of 4 𝑚𝑚2 weighs 20 𝑁 as shown in fig. If the modulus of elasticity for the wire material is 200𝐺𝑃𝑎, find the deflection at C and B. 𝑮𝒊𝒗𝒆𝒏 𝒅𝒂𝒕𝒂: 𝑻𝒐 𝒇𝒊𝒏𝒅: Deflection at C (𝛿𝑙𝑐 ) and B (𝛿𝑙𝐵 )=? 𝐿 = 16 𝑚 = 16 × 103 𝑚𝑚 𝐴 = 4 𝑚𝑚2 𝑊 = 20 𝑁 𝑀𝑜𝑑𝑢𝑙𝑢𝑠 𝑜𝑓 𝑒𝑙𝑎𝑠𝑡𝑖𝑐𝑖𝑡𝑦 𝐸 = 200 𝐺𝑃𝑎 = 200 × 103 Τ 𝑁 𝑚 𝑚2 𝑩 𝑨 𝑪 𝟖 𝒎 𝟖 𝒎 BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY
- 11. 𝑭𝒐𝒓𝒎𝒖𝒍𝒂 ∶ 𝐷𝑒𝑓𝑙𝑒𝑐𝑡𝑖𝑜𝑛 𝑜𝑓𝑤𝑖𝑟𝑒 𝑎𝑡 𝐶 𝑑𝑢𝑒 𝑡𝑜 𝑠𝑒𝑙𝑓 𝑤𝑒𝑖𝑔ℎ𝑡 𝑜𝑓 𝑤𝑖𝑟𝑒 𝐴𝐶 𝛿𝑙𝑐 = 𝑊𝐿 2𝐴𝐸 𝐷𝑒𝑓𝑙𝑒𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 𝑤𝑖𝑟𝑒 𝑎𝑡 𝐵 𝛿𝑙𝐵 = 𝐷𝑒𝑓𝑙𝑒𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 𝑤𝑖𝑟𝑒 𝐴𝐵 𝑑𝑢𝑒 𝑡𝑜 𝑠𝑒𝑙𝑓 𝑤𝑒𝑖𝑔ℎ𝑡 + 𝐷𝑒𝑓𝑙𝑒𝑐𝑡𝑖𝑜𝑛 𝑑𝑢𝑒 𝑡𝑜 𝑤𝑒𝑖𝑔ℎ𝑡 𝑜𝑓 𝑤𝑖𝑟𝑒 𝐵𝐶 𝐷𝑒𝑓𝑙𝑒𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 𝑤𝑖𝑟𝑒 𝑎𝑡 𝐵 𝛿𝑙𝐵 = 𝛿𝑙1 + 𝛿𝑙2 𝐷𝑒𝑓𝑙𝑒𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 𝑤𝑖𝑟𝑒 𝑎𝑡 𝐵 𝑑𝑢𝑒 𝑡𝑜 𝑠𝑒𝑙𝑓 𝑤𝑒𝑖𝑔ℎ𝑡 𝑜𝑓 𝑤𝑖𝑟𝑒 𝐴𝐵 𝛿𝑙1 = WAB × 𝐿𝐴𝐵 2𝐴𝐸 𝐷𝑒𝑓𝑙𝑒𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 𝑤𝑖𝑟𝑒 𝑎𝑡 𝐵 𝑑𝑢𝑒 𝑡𝑜 𝑤𝑒𝑖𝑔ℎ𝑡 𝑜𝑓 𝑤𝑖𝑟𝑒 𝐵𝐶 𝛿𝑙2 = PBC × 𝐿𝐴𝐵 𝐴𝐸 𝑩 𝑨 𝑪 𝟖 𝒎 𝟖 𝒎 BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY
- 12. 𝑺𝒐𝒍𝒖𝒕𝒊𝒐𝒏: 𝐷𝑒𝑓𝑙𝑒𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 𝑤𝑖𝑟𝑒𝑎𝑡 𝐶 𝑑𝑢𝑒 𝑡𝑜 𝑠𝑒𝑙𝑓 𝑤𝑒𝑖𝑔ℎ𝑡 𝑜𝑓 𝑤𝑖𝑟𝑒 𝐴𝐶 𝛿𝑙𝑐 = 𝑊𝐿 2𝐴𝐸 𝑩 𝑨 𝑪 𝟖 𝒎 𝟖 𝒎 𝛿𝑙𝑐 = 20 × 16 × 103 2 × 4 × 200 × 103 𝑫𝒆𝒇𝒍𝒆𝒄𝒕𝒊𝒐𝒏 𝒐𝒇 𝒘𝒊𝒓𝒆 𝒂𝒕 𝑪 𝒅𝒖𝒆 𝒕𝒐 𝒔𝒆𝒍𝒇 𝒘𝒆𝒊𝒈𝒉𝒕 𝒐𝒇 𝒘𝒊𝒓𝒆 𝑨𝑪 𝜹𝒍𝒄 = 𝟎. 𝟐𝒎𝒎 𝛿𝑙𝑐 = 0.2 𝑚𝑚 𝐿 = 16 × 103 𝑚𝑚 𝐴 = 4 𝑚𝑚2 𝑊 = 20 𝑁 𝐸 = 200 × 103 Τ 𝑁 𝑚 𝑚2 BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY
- 13. 𝐷𝑒𝑓𝑙𝑒𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 𝑤𝑖𝑟𝑒𝑎𝑡 𝐵 𝑑𝑢𝑒 𝑡𝑜 𝑠𝑒𝑙𝑓 𝑤𝑒𝑖𝑔ℎ𝑡 𝑜𝑓 𝑤𝑖𝑟𝑒 𝐴𝐵 𝛿𝑙1 = WAB × 𝐿𝐴𝐵 2𝐴𝐸 𝛿𝑙1 = 10 × 8 × 103 2 × 4 × 200 × 103 𝛿𝑙1 = 0.05 𝑚𝑚 𝑫𝒆𝒇𝒍𝒆𝒄𝒕𝒊𝒐𝒏 𝒐𝒇 𝒘𝒊𝒓𝒆 𝒂𝒕 𝑩 𝒅𝒖𝒆 𝒕𝒐 𝒔𝒆𝒍𝒇 𝒘𝒆𝒊𝒈𝒉𝒕 𝒐𝒇 𝒘𝒊𝒓𝒆 𝑨𝑩 𝜹𝒍𝟏 = 𝟎. 𝟎𝟓 𝒎𝒎 𝑩 𝑨 𝑪 𝟖 𝒎 𝟖 𝒎 𝐿𝐴𝐵 = 8 × 103 𝑚𝑚 𝐴 = 4 𝑚𝑚2 𝑊 = 20 𝑁 𝐸 = 200 × 103 Τ 𝑁 𝑚 𝑚2 𝑊𝐴𝐵 = W 2 = 10 𝑁 BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY
- 14. 𝑩 𝑨 𝑪 𝟖 𝒎 𝟖 𝒎 𝐷𝑒𝑓𝑙𝑒𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 𝑤𝑖𝑟𝑒𝑎𝑡 𝐵 𝑑𝑢𝑒 𝑡𝑜 𝑤𝑒𝑖𝑔ℎ𝑡 𝑜𝑓 𝑤𝑖𝑟𝑒 𝐵𝐶 𝛿𝑙2 = P × 𝐿𝐴𝐵 𝐴𝐸 𝛿𝑙2 = 10 × 8 × 103 4 × 200 × 103 𝛿𝑙2 = 0.1 𝑚𝑚 𝑫𝒆𝒇𝒍𝒆𝒄𝒕𝒊𝒐𝒏 𝒐𝒇 𝒘𝒊𝒓𝒆 𝒂𝒕 𝑩 𝒅𝒖𝒆 𝒕𝒐 𝒘𝒆𝒊𝒈𝒉𝒕 𝒐𝒇 𝒘𝒊𝒓𝒆 𝑩𝑪 𝜹𝒍𝟐 = 𝟎. 𝟏 𝒎𝒎 𝐿AB = 8 × 103 𝑚𝑚 𝐴 = 4 𝑚𝑚2 𝑊 = 20 𝑁 𝐸 = 200 × 103 Τ 𝑁 𝑚 𝑚2 P = W 2 = 10 𝑁 BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY
- 15. 𝑩 𝑨 𝑪 𝟖 𝒎 𝟖 𝒎 𝐷𝑒𝑓𝑙𝑒𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 𝑤𝑖𝑟𝑒𝑎𝑡 𝐵 𝛿𝑙𝐵 = 𝛿𝑙1 + 𝛿𝑙2 𝛿𝑙𝐵 = 0.05 + 0.1 𝑫𝒆𝒇𝒍𝒆𝒄𝒕𝒊𝒐𝒏 𝒐𝒇 𝒘𝒊𝒓𝒆 𝒂𝒕 𝑩 𝜹𝒍𝑩 = 𝟎. 𝟏𝟓 𝒎𝒎 𝛿𝑙1 = 0.05 𝑚𝑚 𝛿𝑙2 = 0.1 𝑚𝑚 BIBIN.C / ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY
- 16. Thank You BIBIN.C /ASSOCIATE PROFESSOR / MECHANICAL ENGINEERING / RMK COLLEGE OF ENGINEERING AND TECHNOLOGY