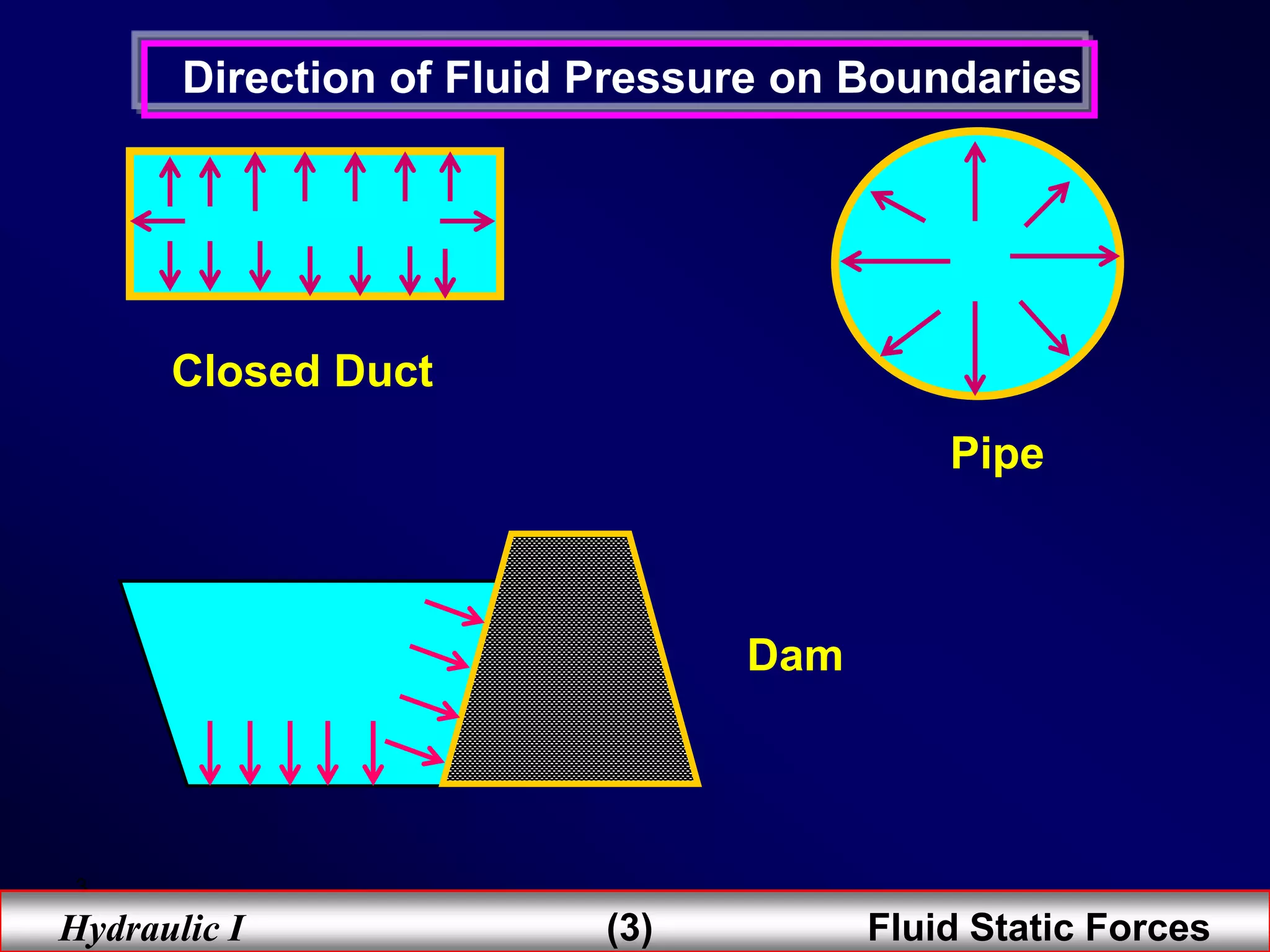
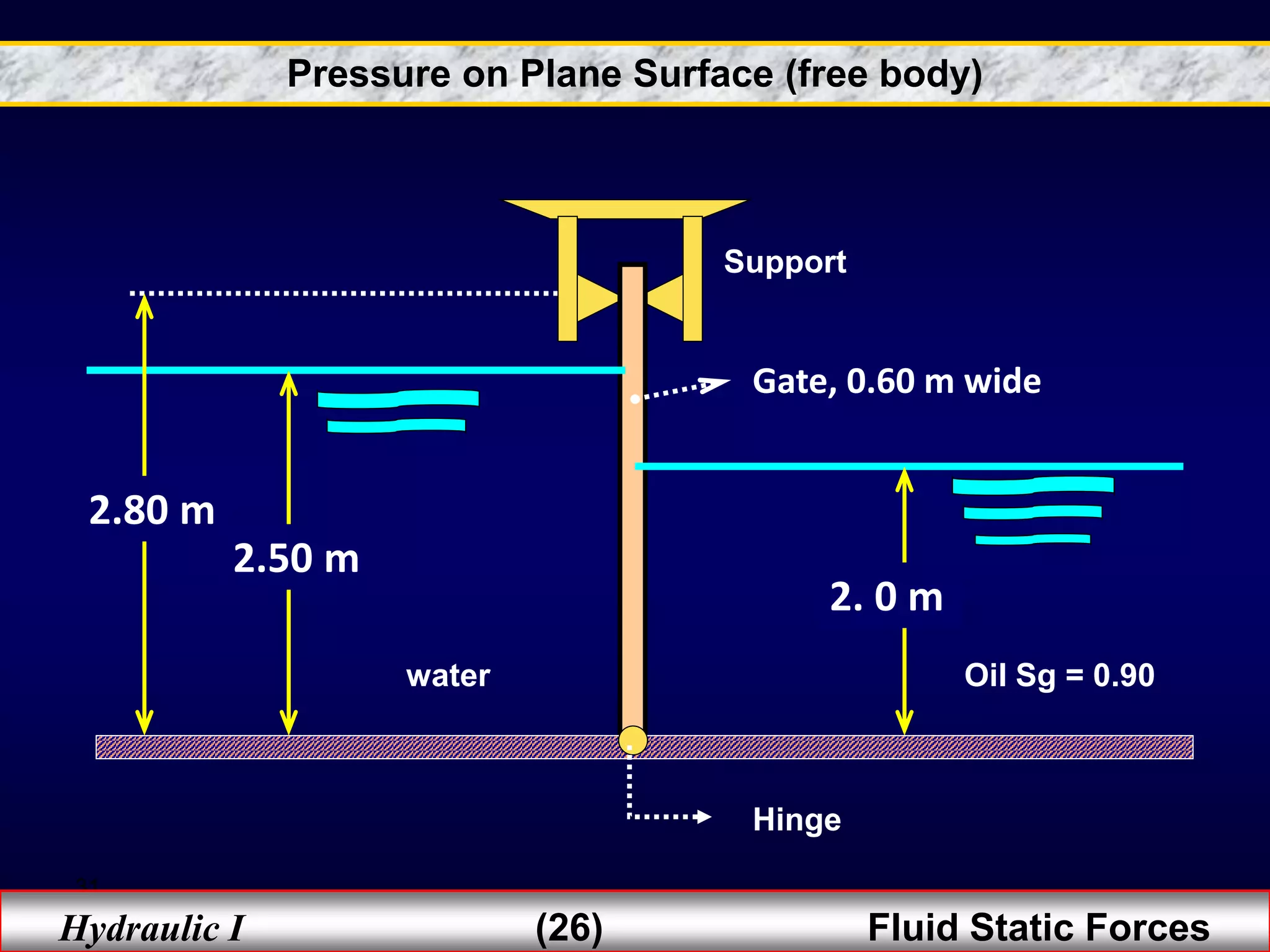
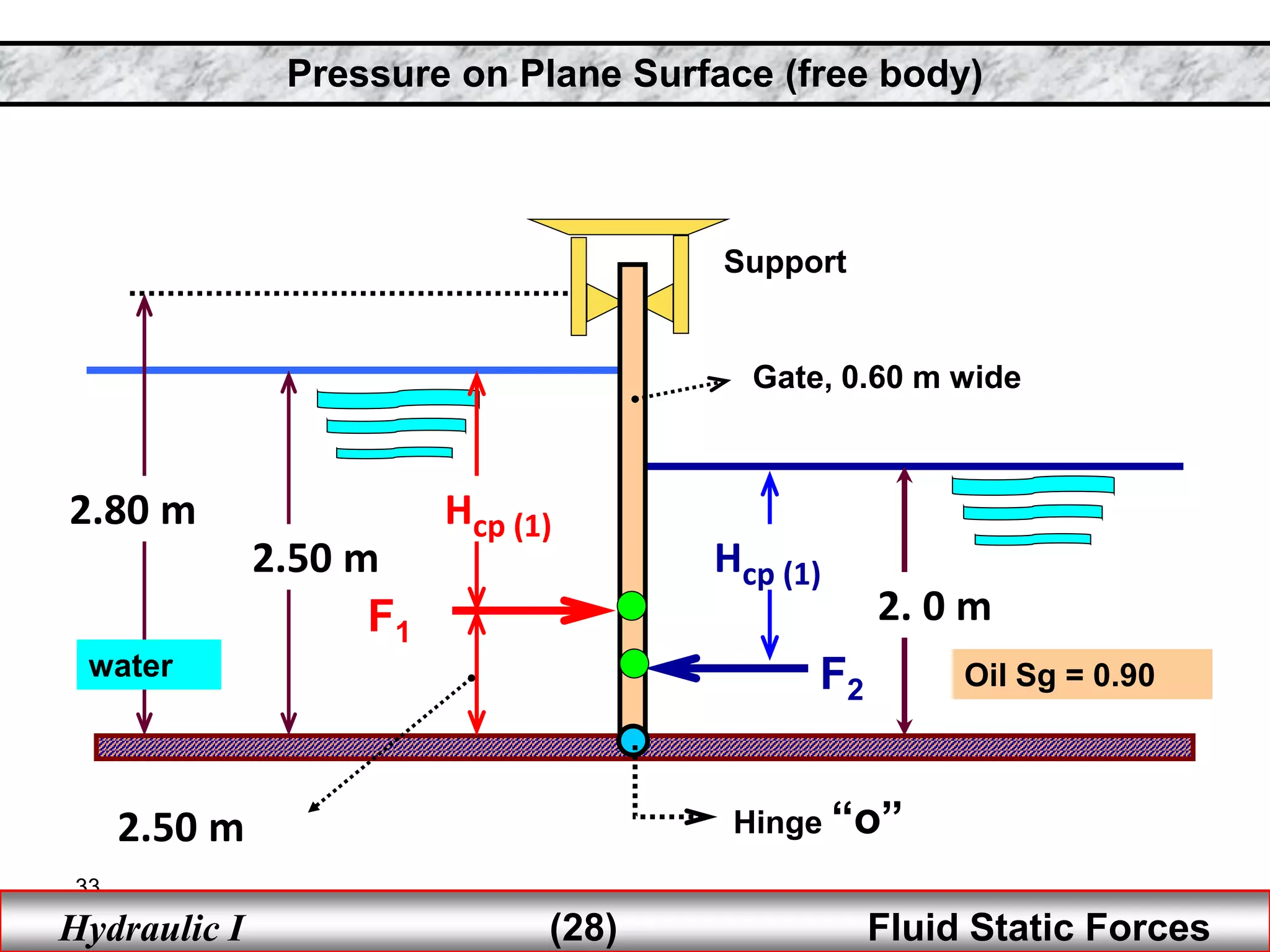
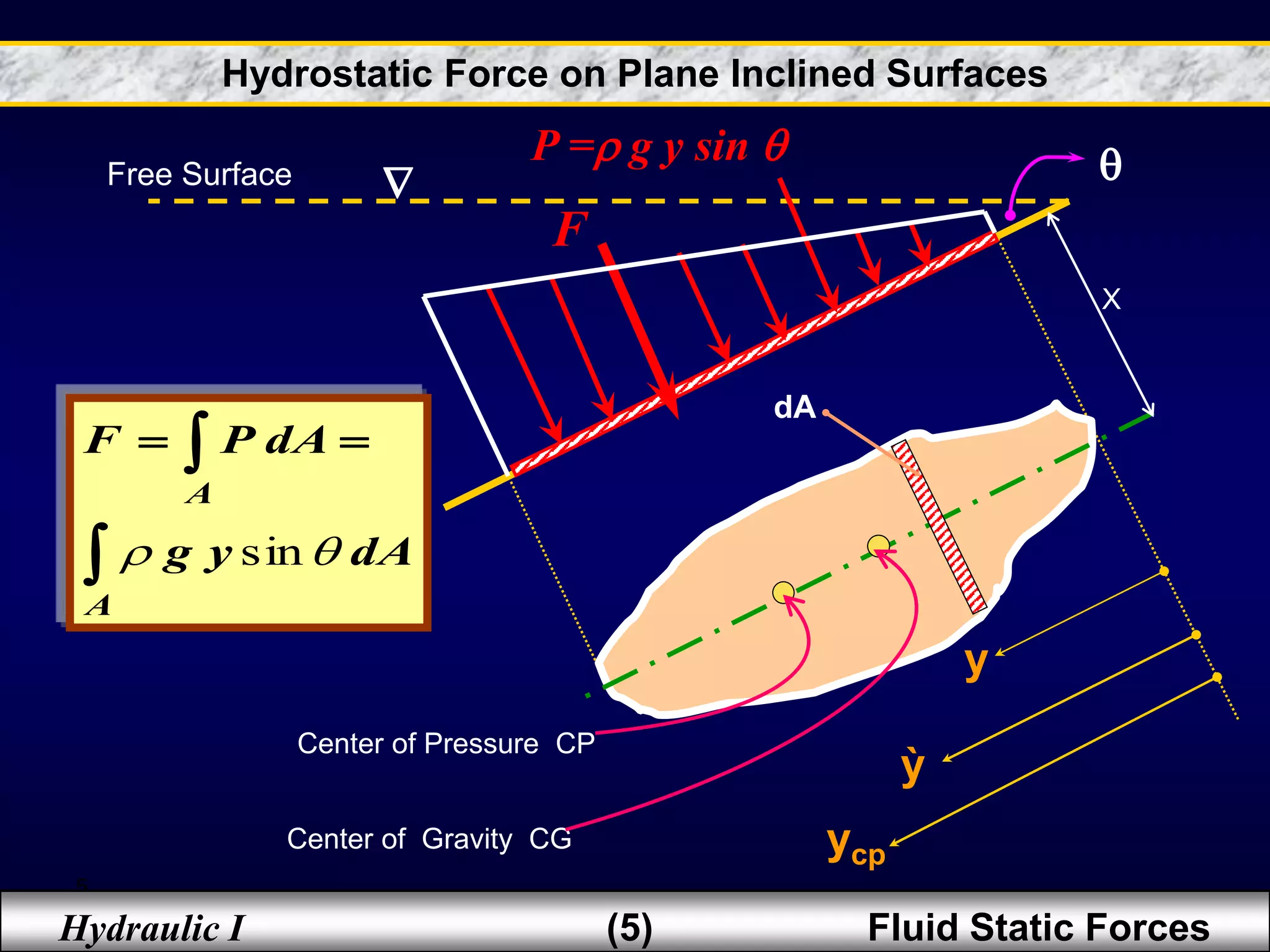
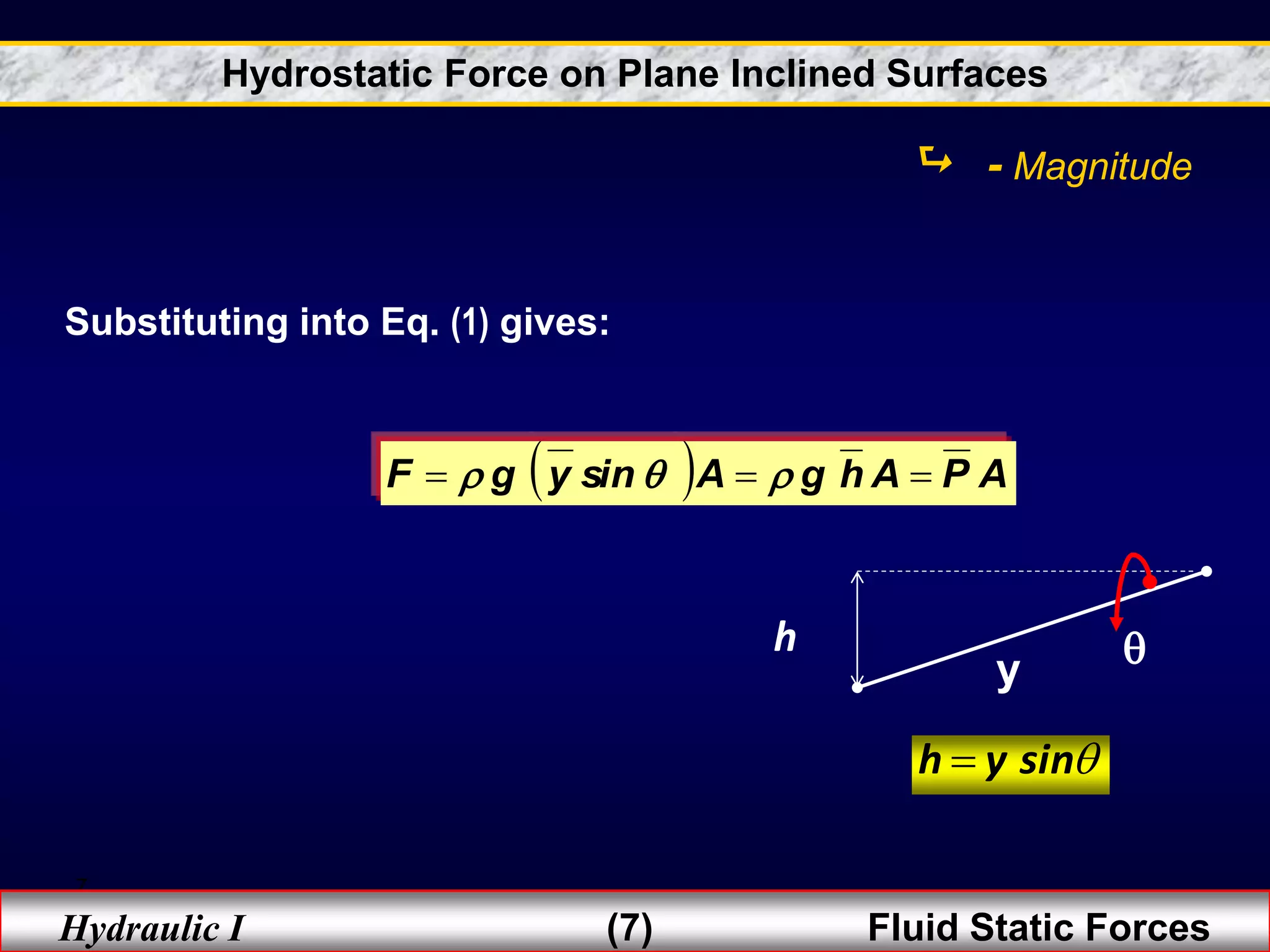
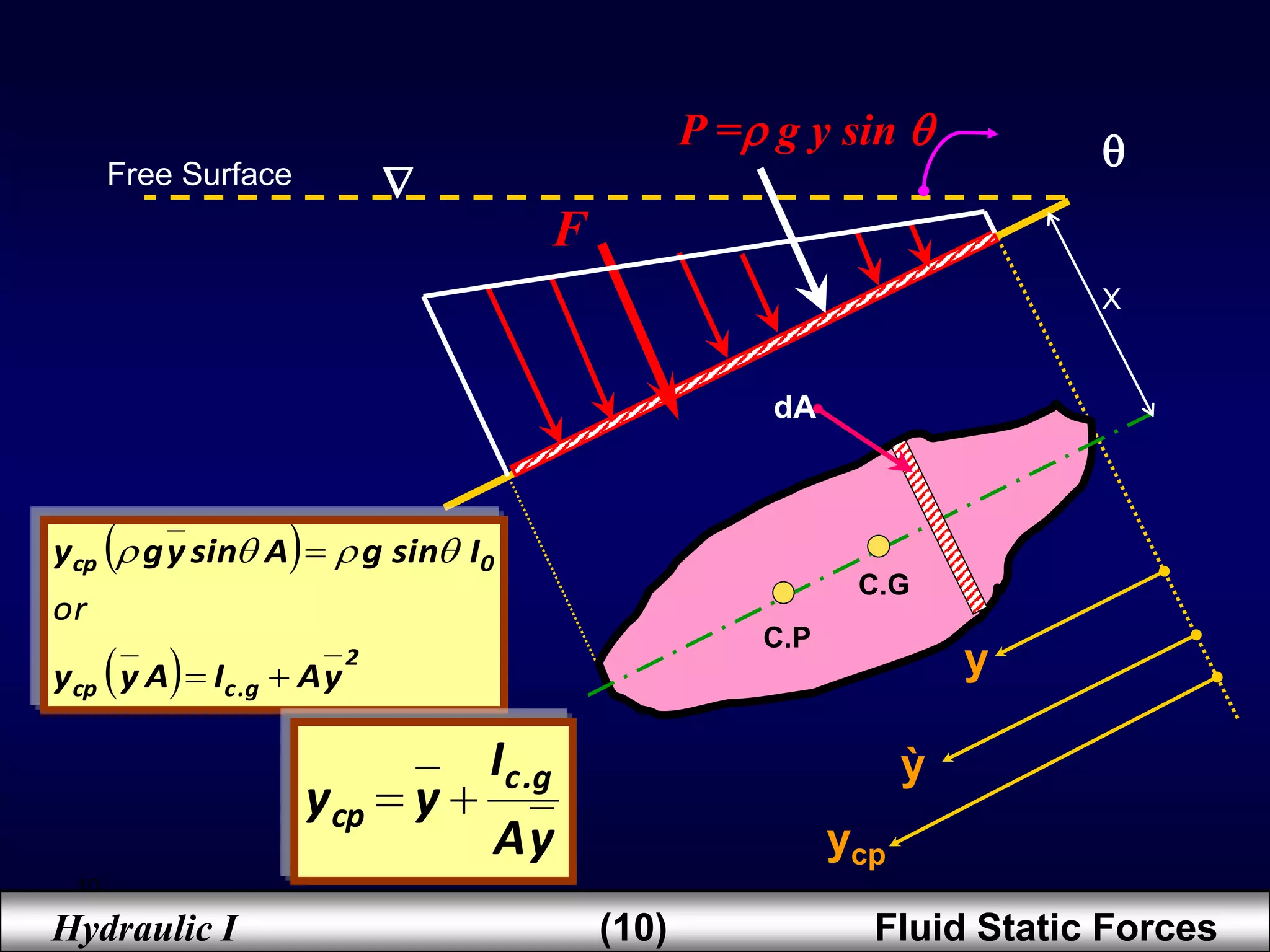
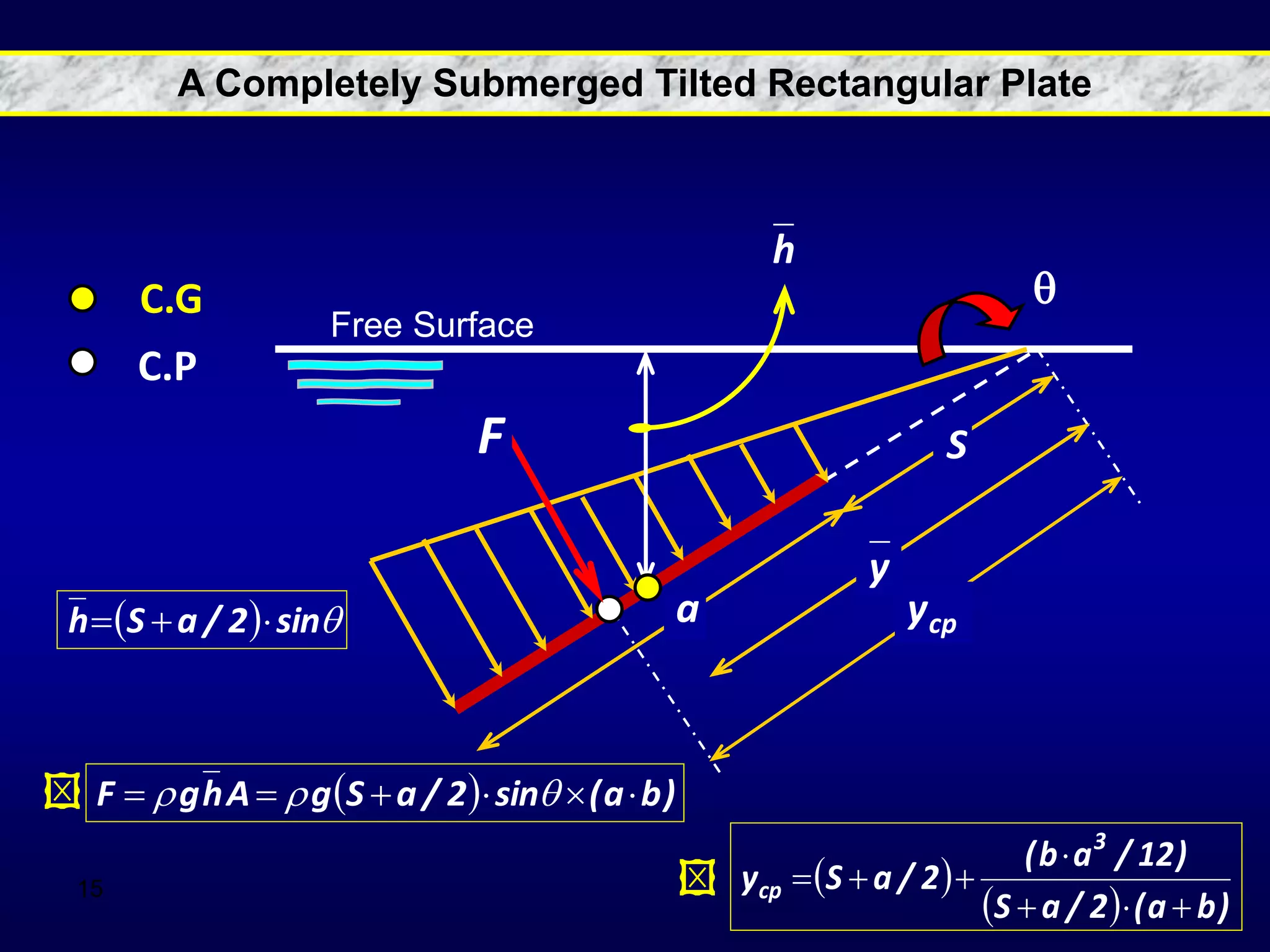
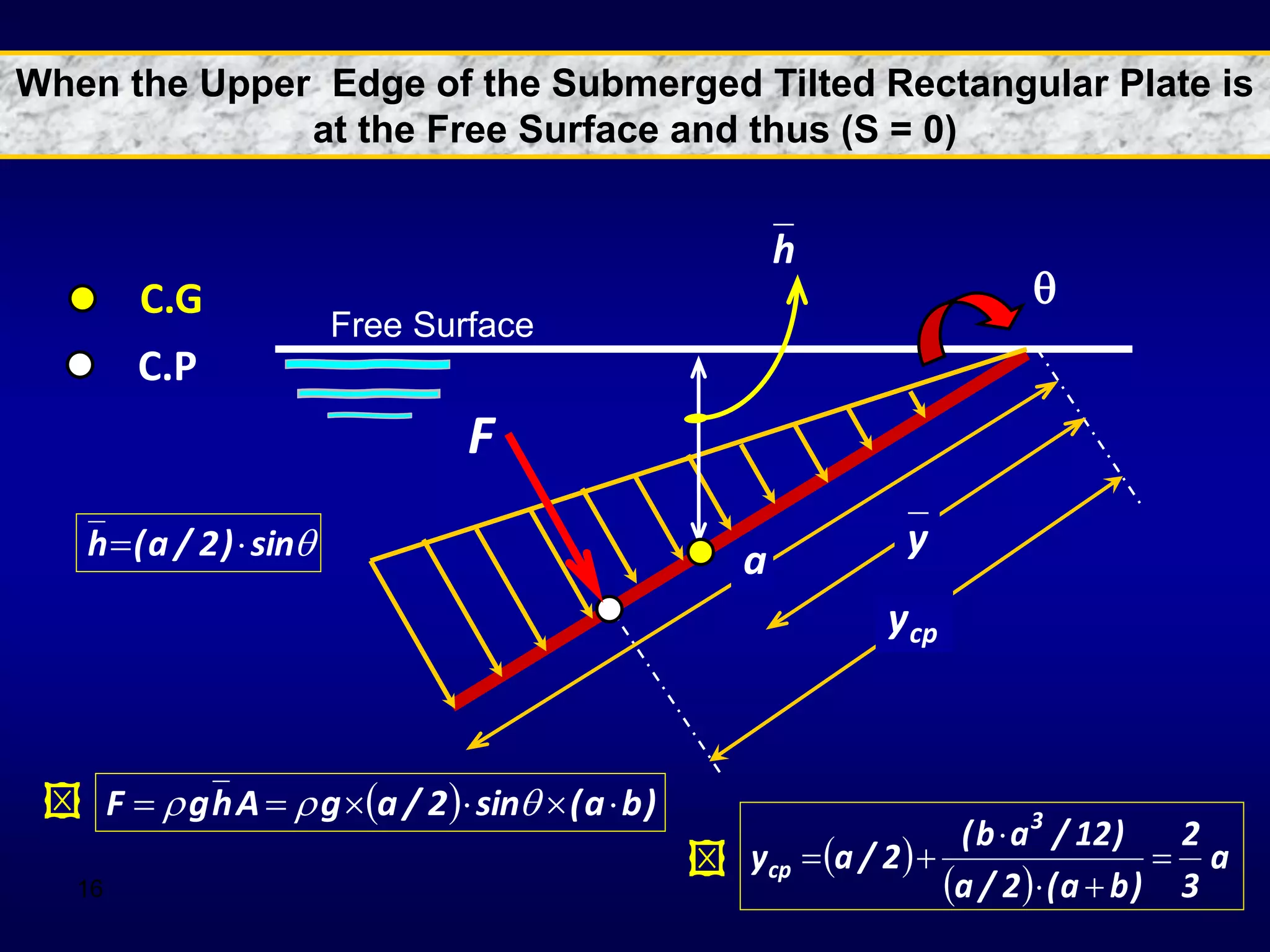
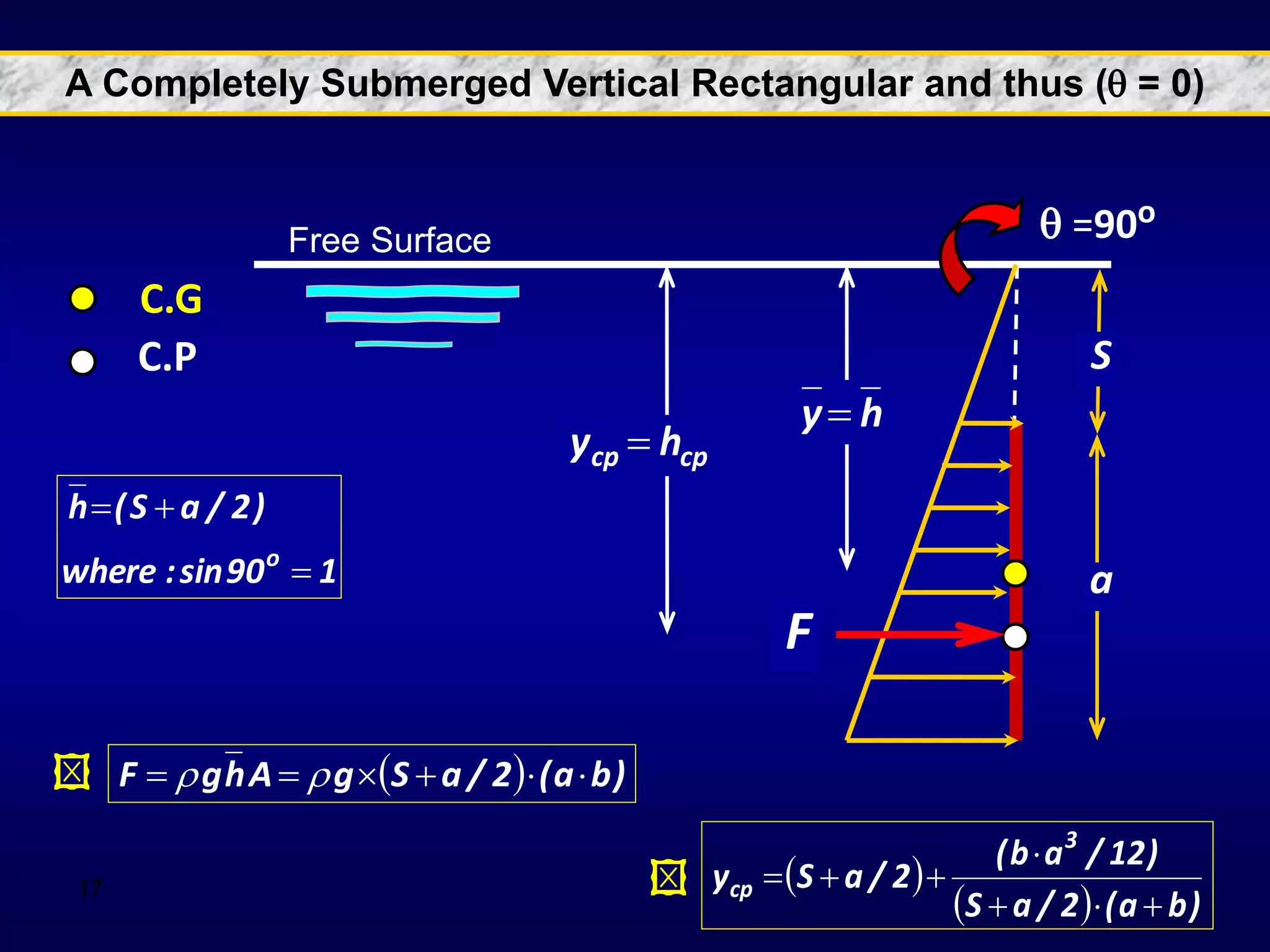
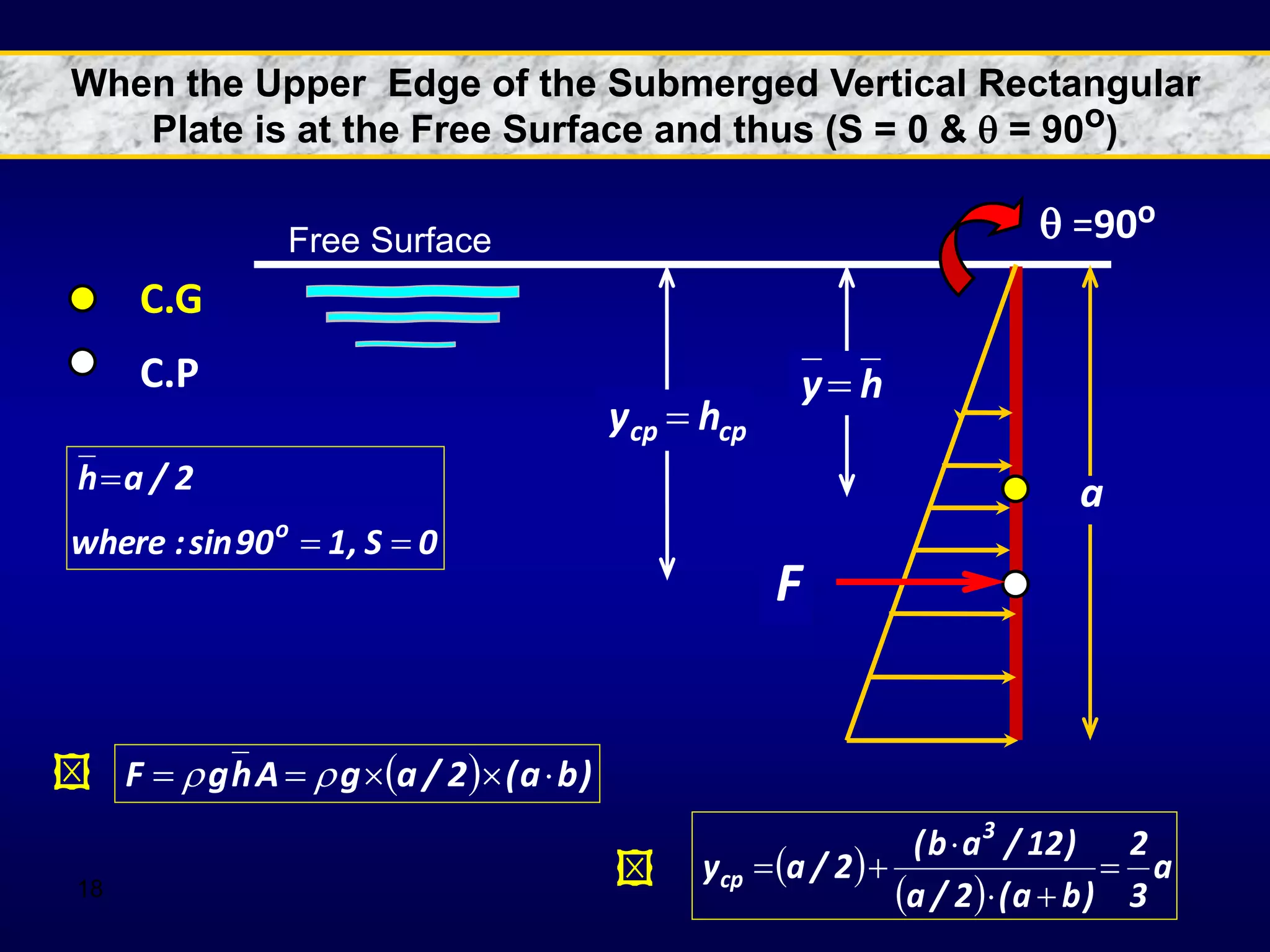
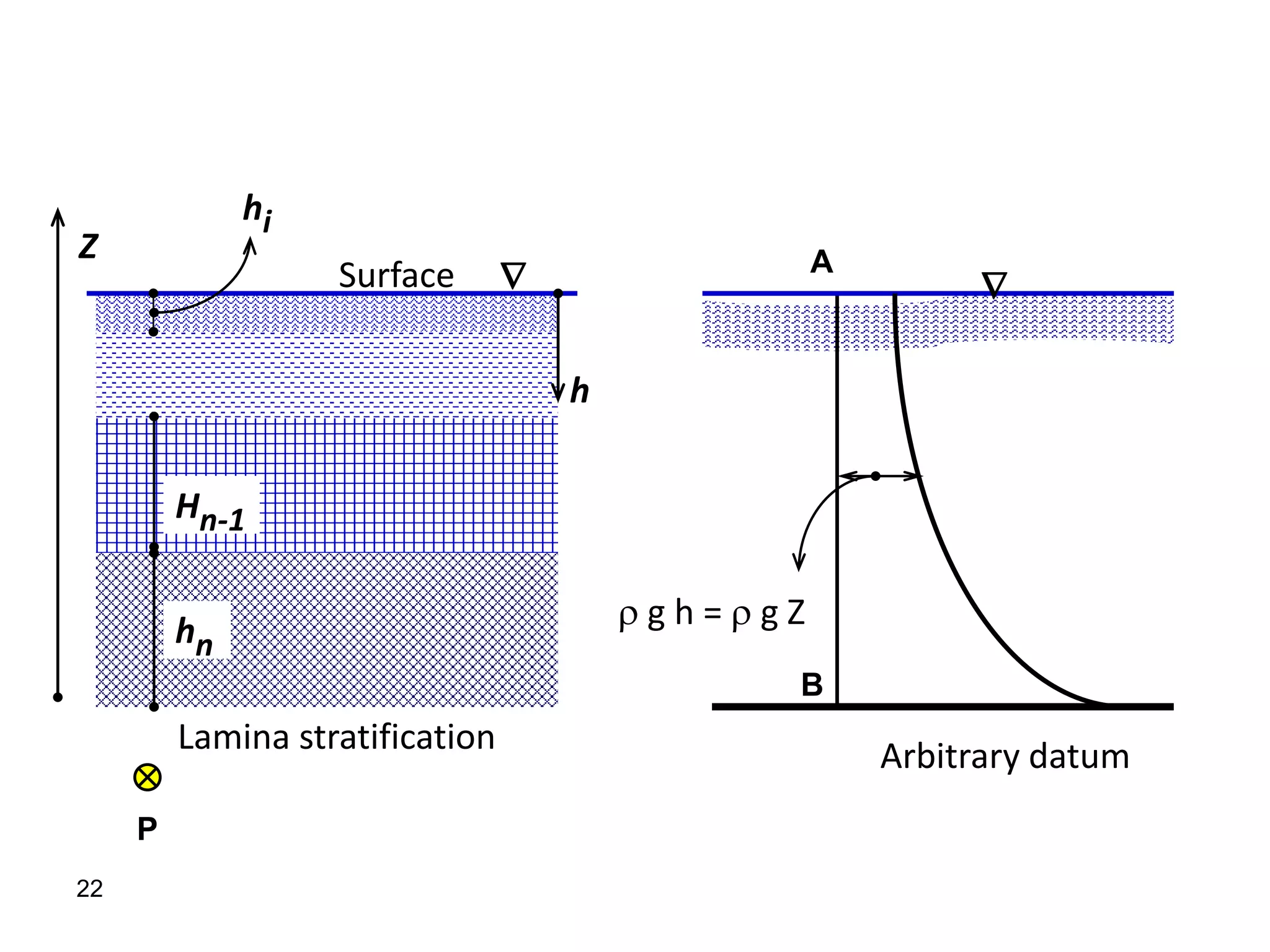
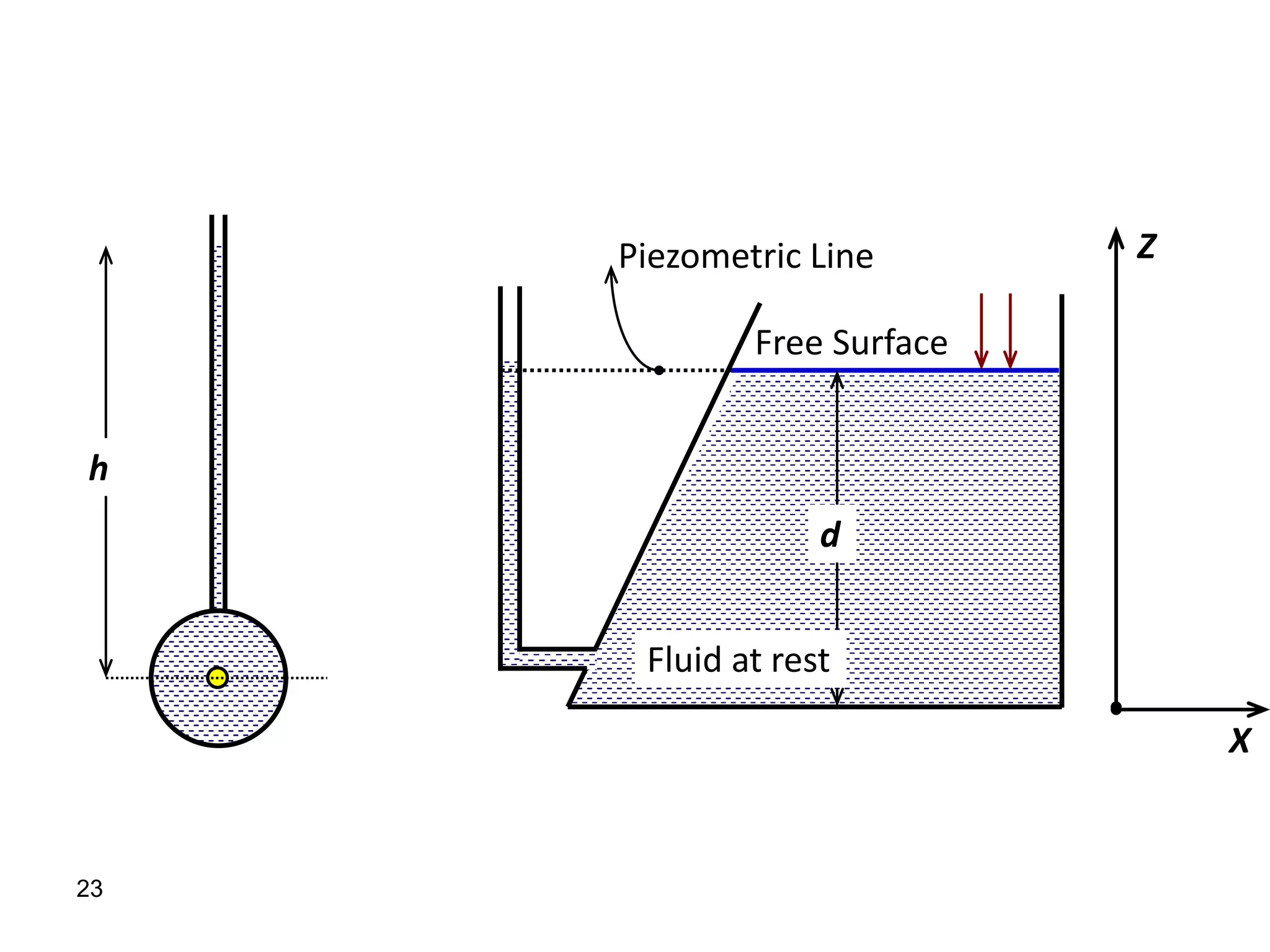
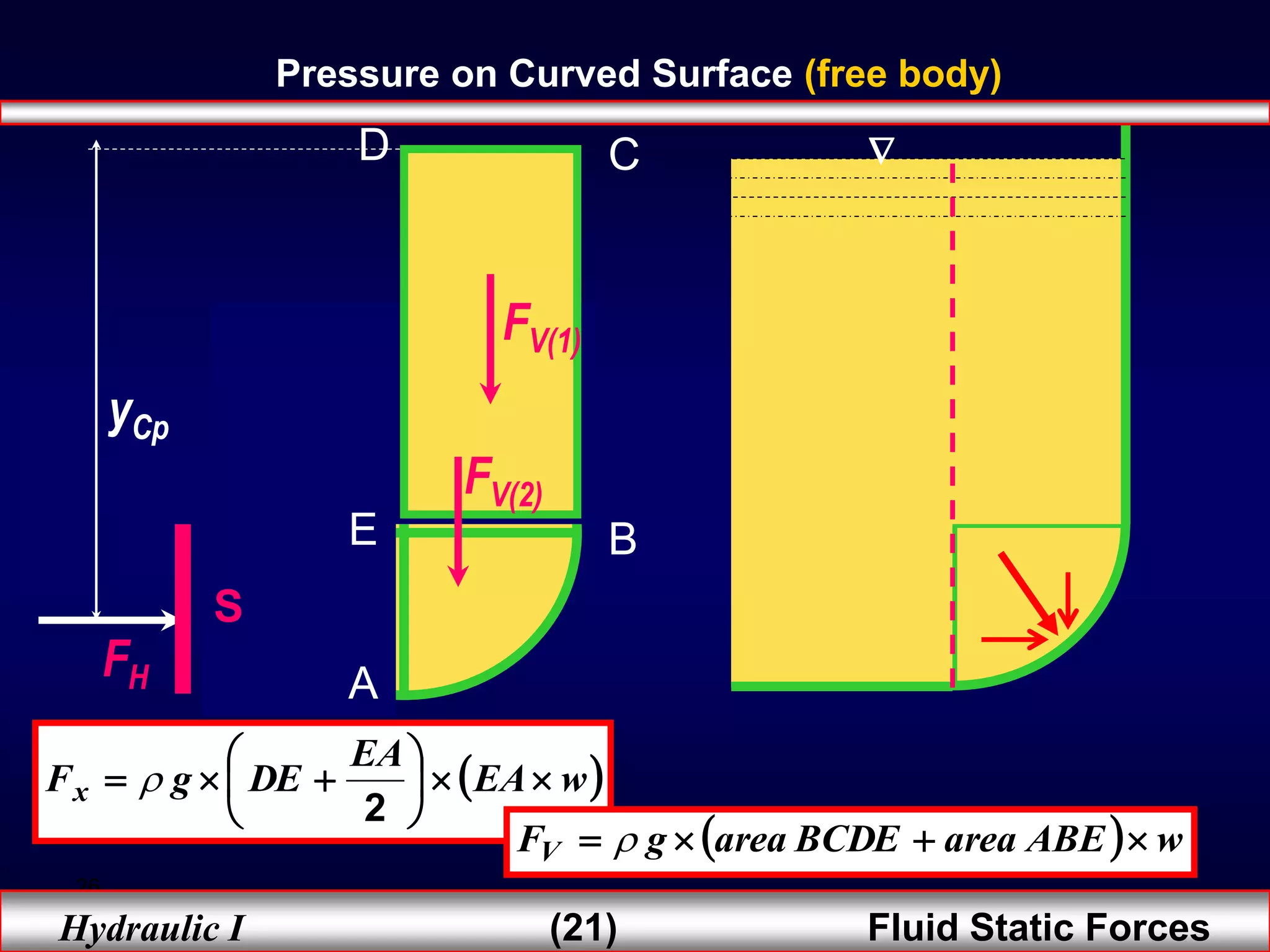
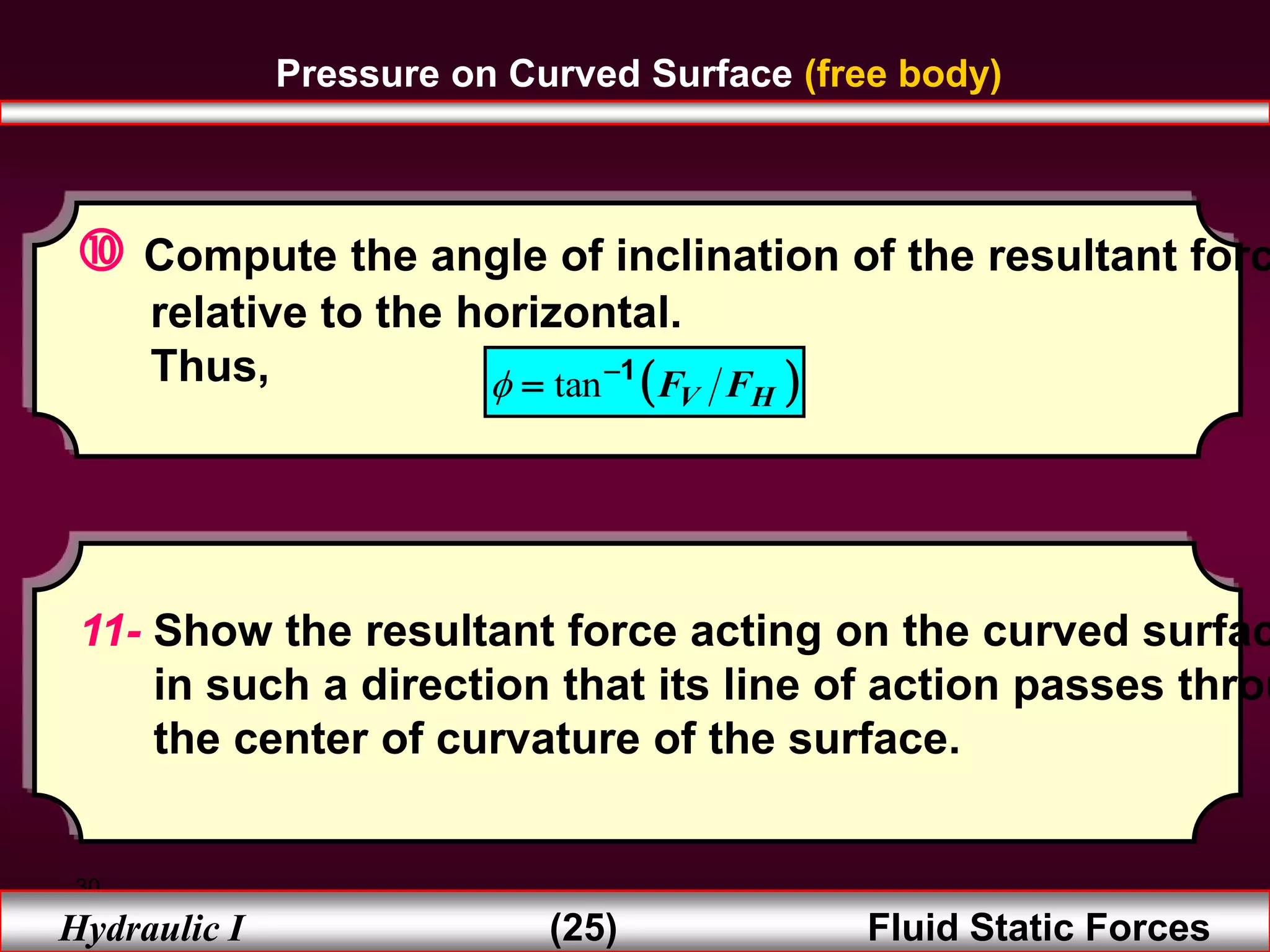
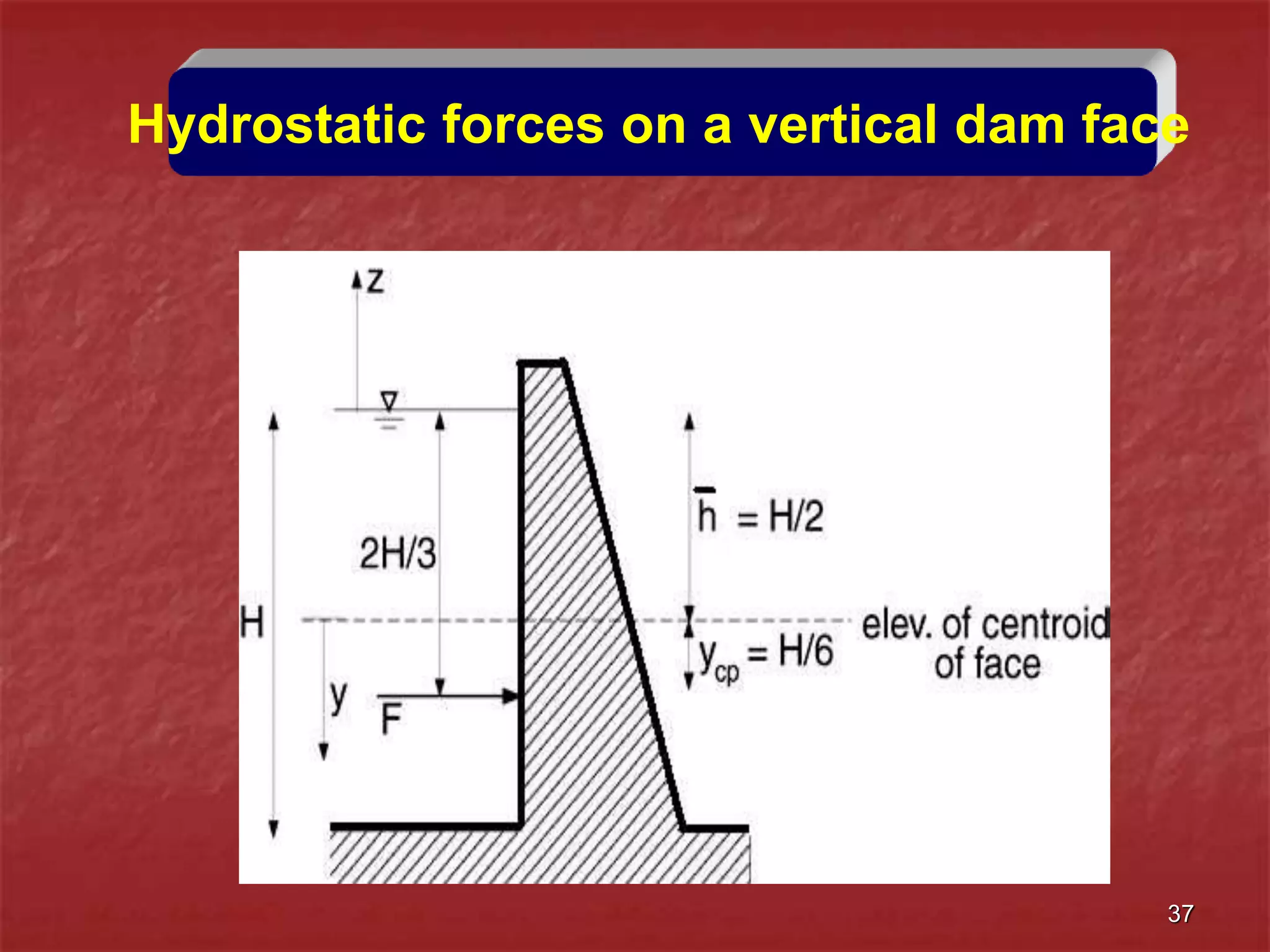
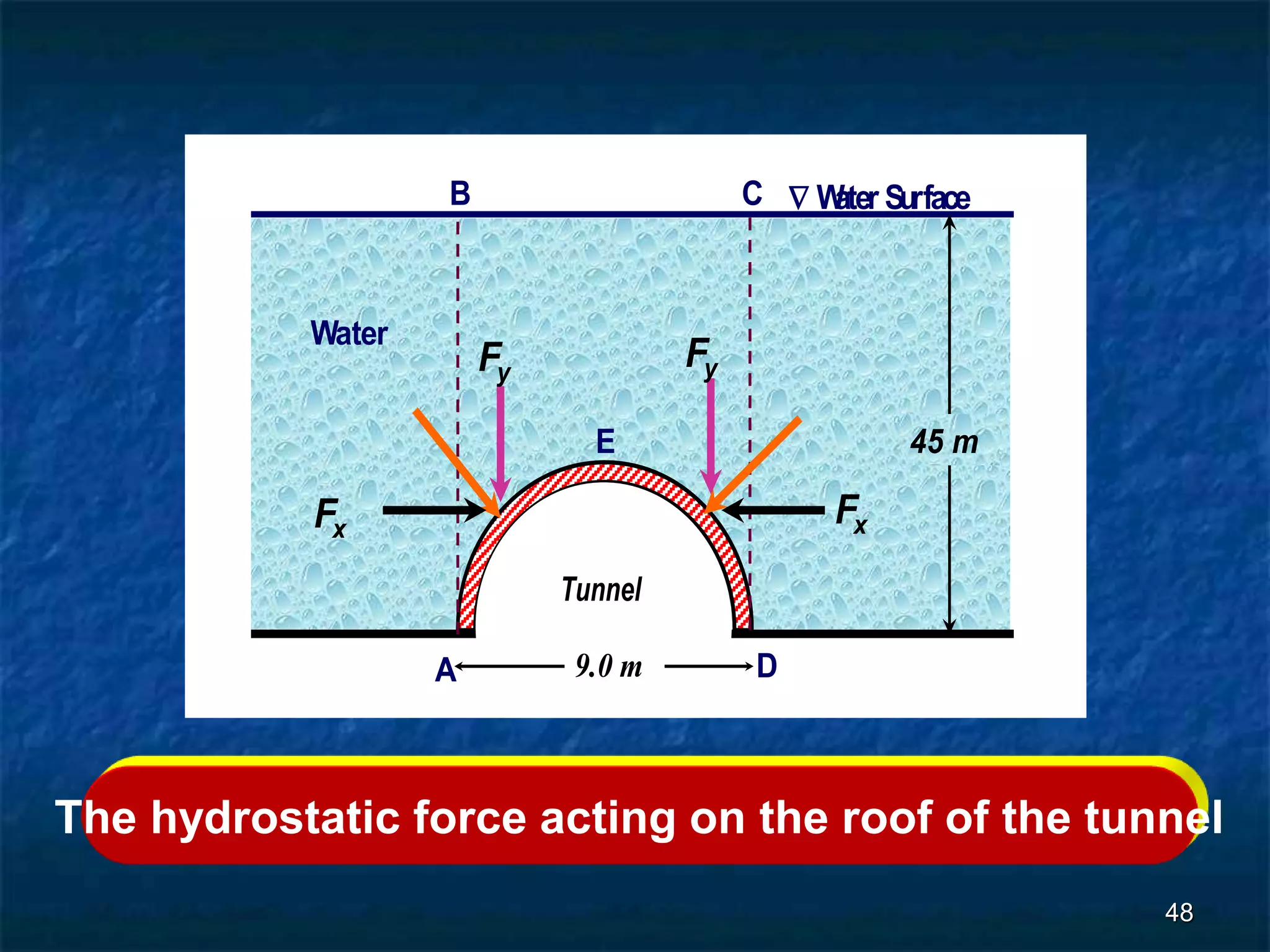
1. Fluid static forces act on surfaces exposed to fluids due to pressure distributions in the fluid. The magnitude and direction of these forces depend on factors like the surface geometry, depth of submergence, and fluid properties. 2. Hydrostatic forces can be resolved into vertical and horizontal components, with the vertical force equal to the weight of the displaced fluid. The location of the center of pressure determines the line of action of the resultant force. 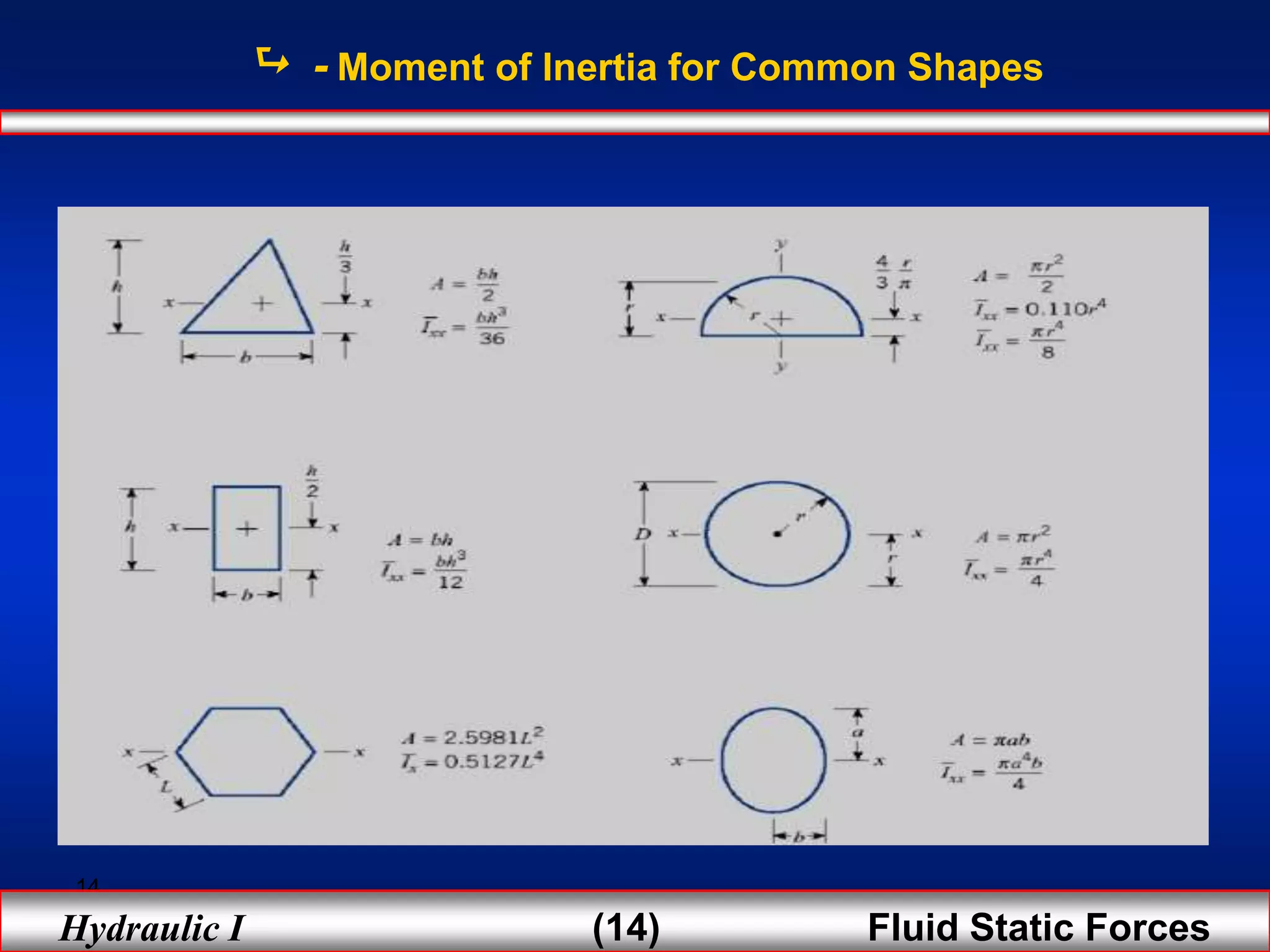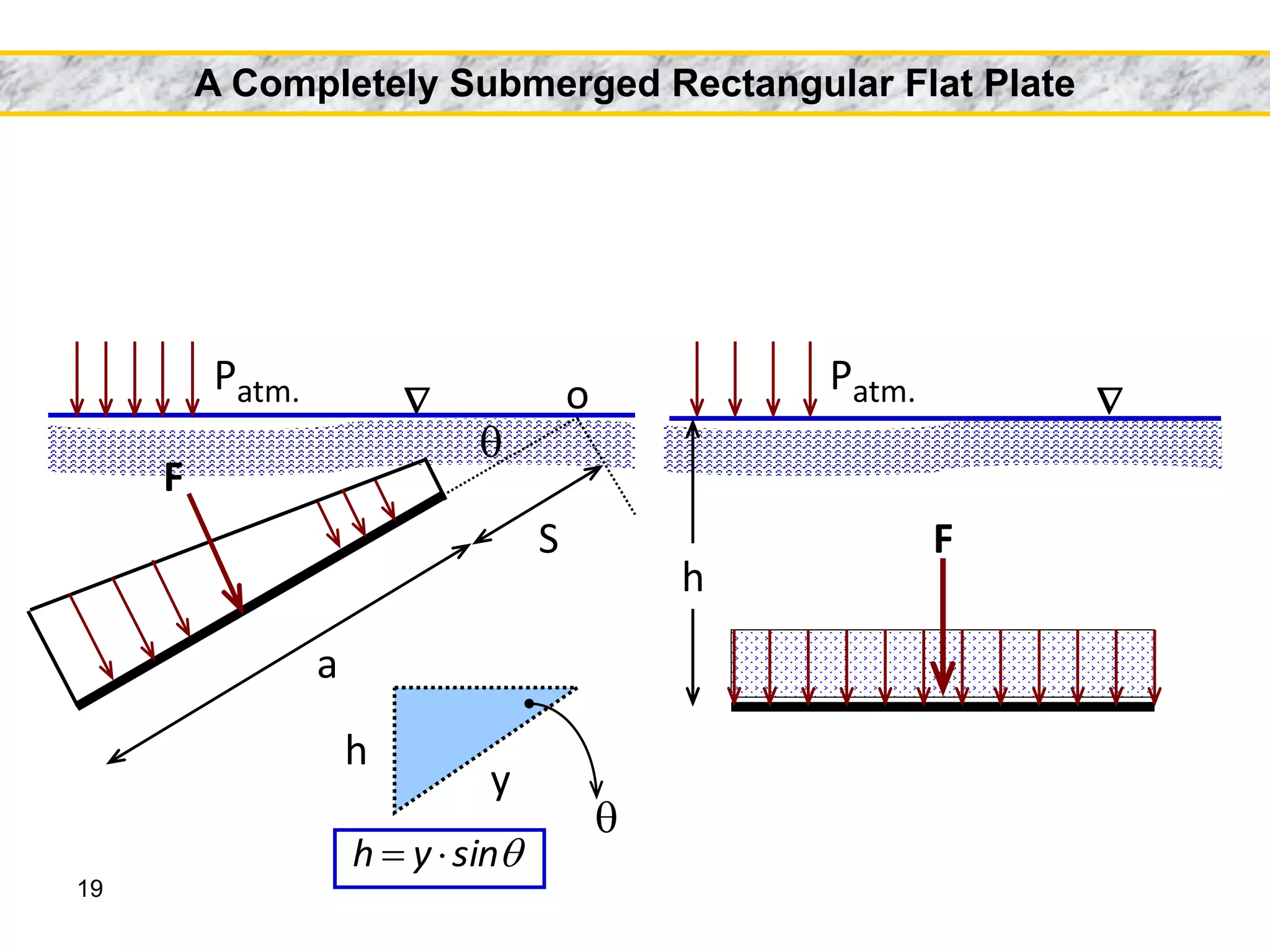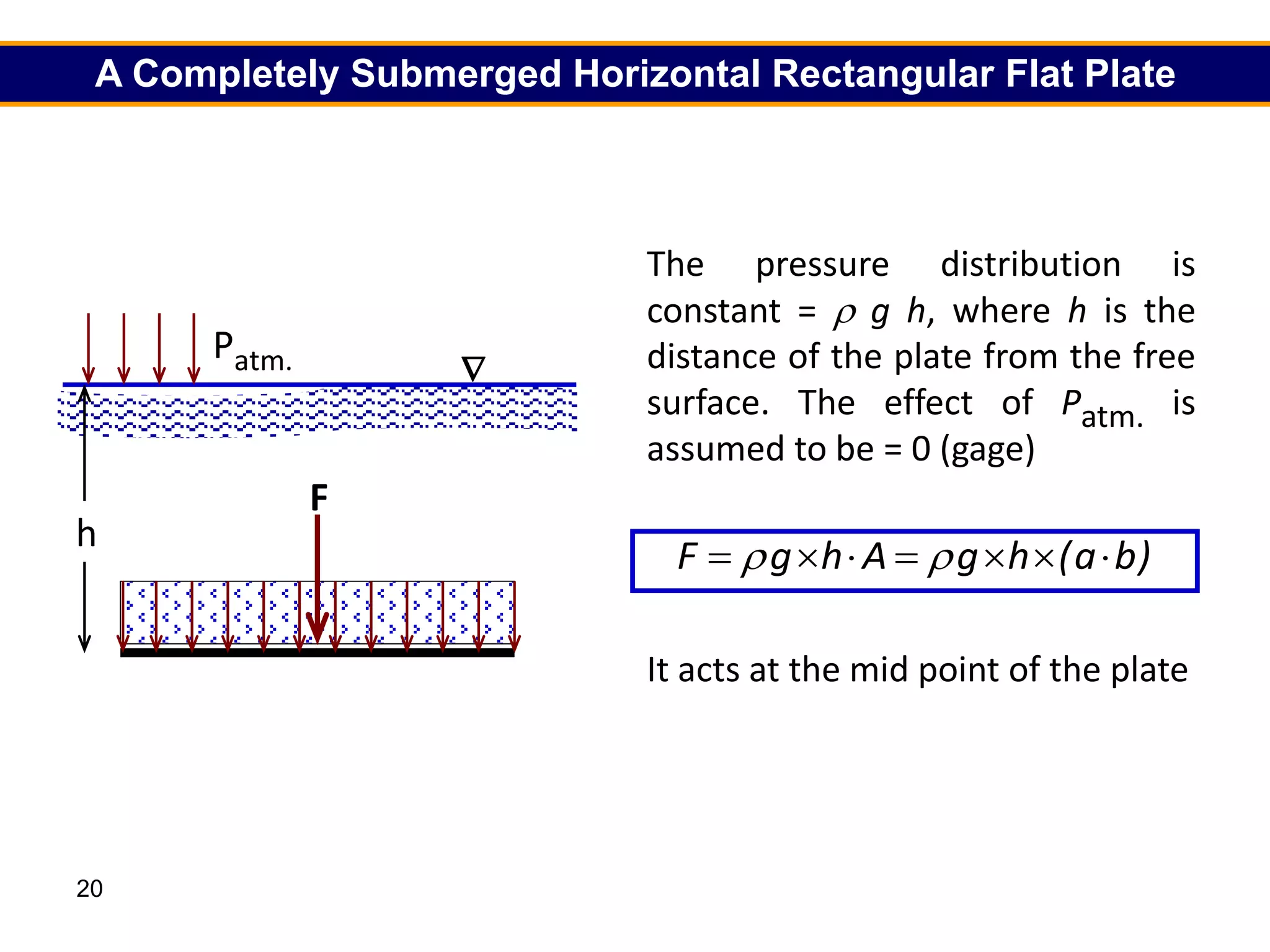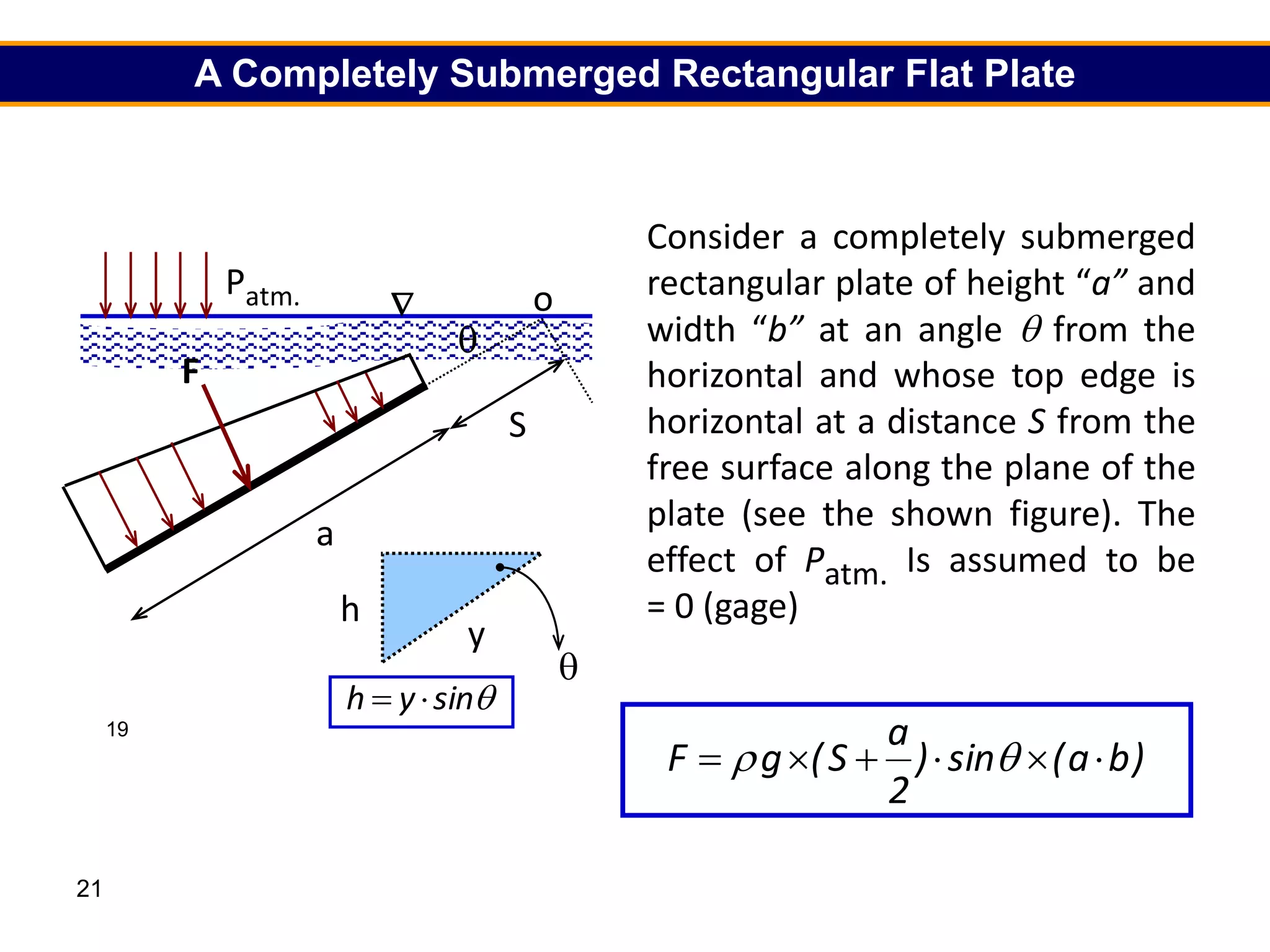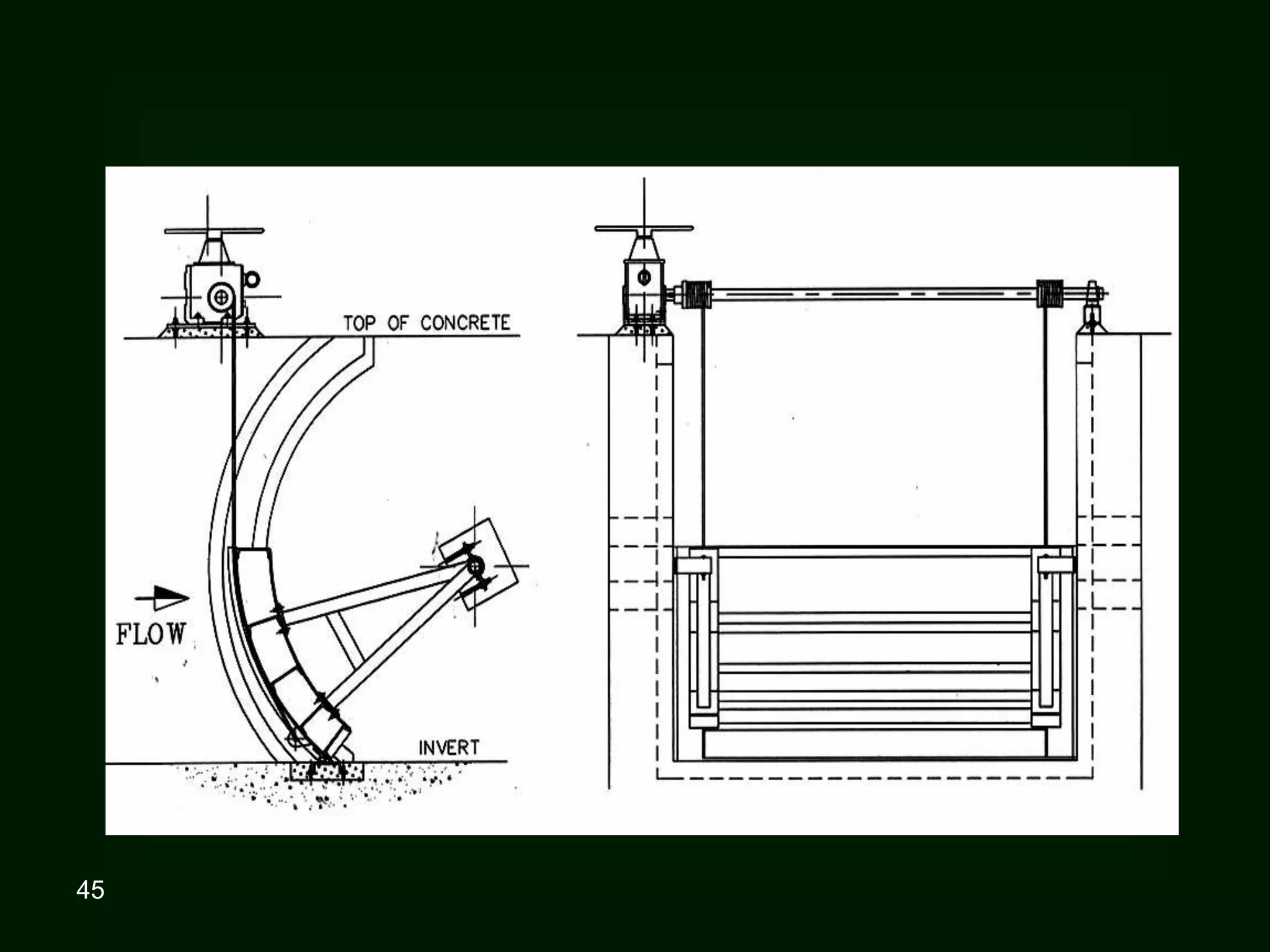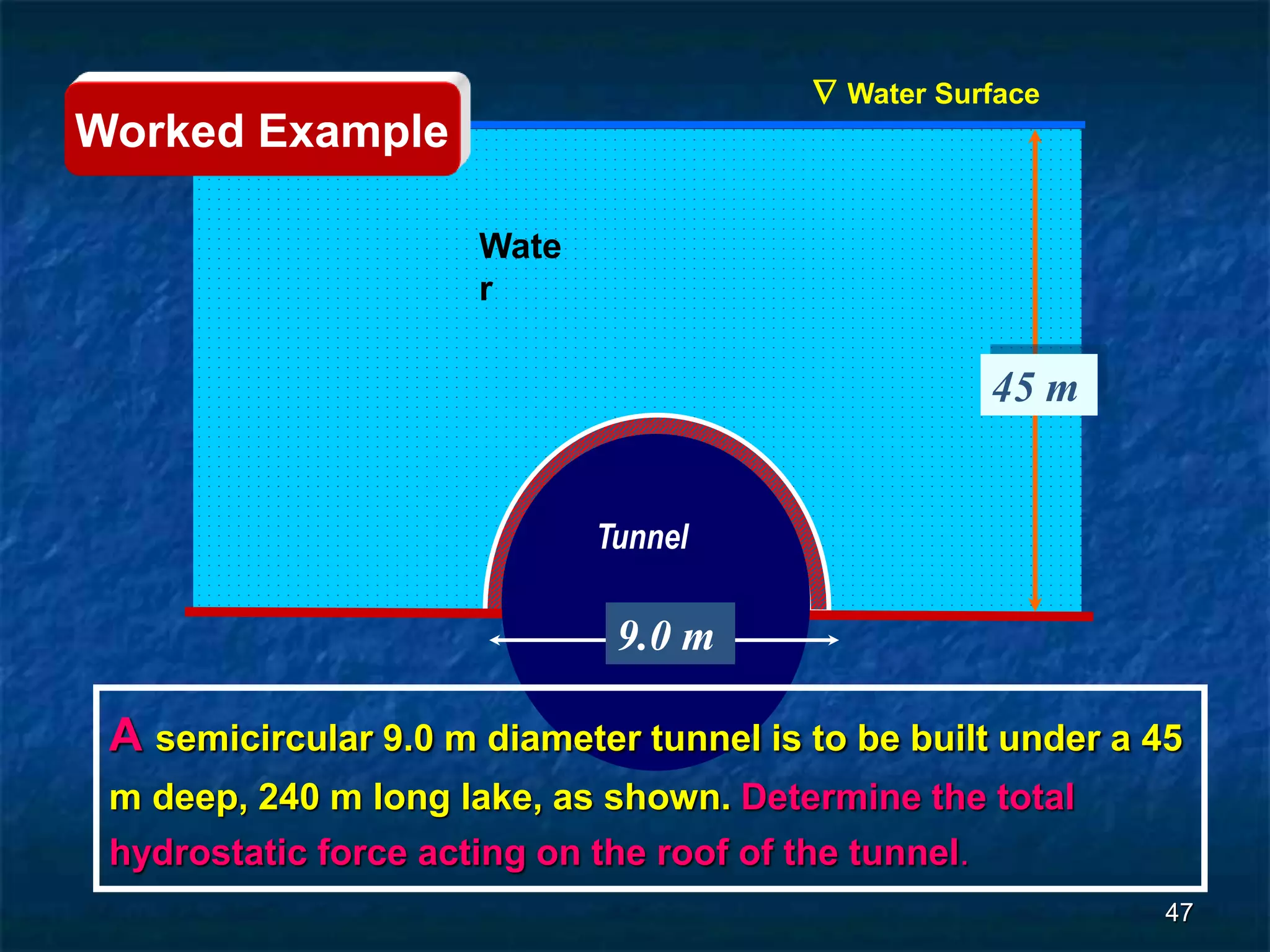3. For regular shapes, equations are provided to calculate the hydrostatic forces and location of the center of pressure based on the surface dimensions and submergence depth. Examples of applying these concepts to dams, gates, and curved surfaces are also presented.

1. 1
Fluid Static Forces
By:
Dr: Ezzat El-sayed Gomaa

2. 2
Hydraulic I (2) Fluid Static Forces
Hydrostatic Forces on Plane Surfaces
- Magnitude,
 - Direction, it is the easiest !
Why ?
 - Line of action
 To define the force, we need:

3. 3
Closed Duct
Pipe
Dam
Hydraulic I (3) Fluid Static Forces
Direction of Fluid Pressure on Boundaries

4. 4
Hydraulic I (4) Fluid Static Forces
Hydrostatic Force on an Inclined Plane
Surfaces
 - Magnitude,
 - Location

5. 5
X
dA
Hydraulic I (5) Fluid Static Forces
Center of Pressure CP
Center of Gravity CG
y
ỳ
ycp


F
P = g y sin 
Free Surface

 

A
A
dA
y
g
dA
P
F

 sin
Hydrostatic Force on Plane Inclined Surfaces

6. 6
Hydraulic I (6) Fluid Static Forces
A
y
sin
g
dA
sin
y
g
dA
P
F
A
A
A


 

 



Surfaces exposed to fluids experience a force due to the
distribution in the fluid
From solid mechanics the location of the center of gravity
(centroid of the area) measured from the surface is
A
y
A
y
A


1
..(1)
 - Magnitude
Hydrostatic Force on Plane Inclined Surfaces

7. 7
Hydraulic I (7) Fluid Static Forces
  A
P
A
h
g
A
sin
y
g
F 

 


Substituting into Eq. (1) gives:
y
h 

sin
y
h 
 - Magnitude
Hydrostatic Force on Plane Inclined Surfaces

8. 8
Hydraulic I (8) Fluid Static Forces
A
P
A
h
g
A
P
A
h
g
A
P
F atm
atm
)
R
(







The net pressure force on the plane, submerged surface is
 - Note
Hydrostatic Force on Plane Surfaces

9. 9
Hydraulic I (9) Fluid Static Forces
Center of Pressure on an Inclined Plane Surface
 - Line of Action of F
Does the resultant force pass thought the center of
gravity ?
 No! lies below the centroid, since pressure
increases with depth
 Moment of the resultant force must equal the
moment of the distributed pressure force
dA
y
g
y
dF
y
F
A
A
cp 
 
 2

 sin

10. 10
X
dA
Hydraulic I (10) Fluid Static Forces
y
ỳ
ycp


F
P = g y sin 
Free Surface
 
  2
g
.
c
cp
0
cp
y
A
I
A
y
y
I
sin
g
A
sin
y
g
y



or




C.G
C.P
y
A
I
y
y g
.
c
cp 


11. 11
Hydraulic I (11) Fluid Static Forces
 - Line of Action of F (center of pressure)
 The location of the center of pressure is
independent of the angle ,
 The center of pressure is always below the
centroid,
 As the depth of immersion increase, the depth of
the center of pressure approaches the centroid.
y
A
I
y
y g
.
c
cp 


12. 12
Hydraulic I (12) Fluid Static Forces
 - Hoover Dam

13. 13
Hydraulic I (13) Fluid Static Forces
 - Hoover Dam

14. 14
Hydraulic I (14) Fluid Static Forces
 - Moment of Inertia for Common Shapes

15. 15

C.G
C.P
Free Surface
A Completely Submerged Tilted Rectangular Plate
  )
b
a
(
sin
2
/
a
S
g
A
h
g
F 




 


 
  )
b
a
(
2
/
a
S
)
12
/
a
b
(
2
/
a
S
y
3
cp







  
sin
2
/
a
S
h 


h
y
cp
y
S
F
a



16. 16

C.G
C.P
Free Surface

sin
)
2
/
a
(
h 
 y
a
cp
y
F
  )
b
a
(
sin
2
/
a
g
A
h
g
F 




 


h
 
 
a
3
2
)
b
a
(
2
/
a
)
12
/
a
b
(
2
/
a
y
3
cp 





When the Upper Edge of the Submerged Tilted Rectangular Plate is
at the Free Surface and thus (S = 0)



17. 17
 =90o
C.G
C.P
Free Surface
A Completely Submerged Vertical Rectangular and thus ( = 0)
a
S
1
90
sin
:
where
)
2
/
a
S
(
h
o



cp
cp h
y 
h
y
F
  )
b
a
(
2
/
a
S
g
A
h
g
F 




 

 
  )
b
a
(
2
/
a
S
)
12
/
a
b
(
2
/
a
S
y
3
cp










18. 18
 =90o
C.G
C.P
Free Surface
h
y
cp
cp h
y 
0
S
,
1
90
sin
:
where
2
/
a
h
o


 a
F
When the Upper Edge of the Submerged Vertical Rectangular
Plate is at the Free Surface and thus (S = 0 &  = 90o)
  )
b
a
(
2
/
a
g
A
h
g
F 



 

 
 
a
3
2
)
b
a
(
2
/
a
)
12
/
a
b
(
2
/
a
y
3
cp 








19. 19
S
a
o

Patm. Patm.
h


F
y
h

F

sin
y
h 

A Completely Submerged Rectangular Flat Plate

20. 20
Patm.
h


F
A Completely Submerged Horizontal Rectangular Flat Plate
The pressure distribution is
constant =  g h, where h is the
distance of the plate from the free
surface. The effect of Patm. is
assumed to be = 0 (gage)
)
b
a
(
h
g
A
h
g
F 





 

It acts at the mid point of the plate

21. 21
19
S
a
o

Patm. Patm.
h


F
y
h

F

sin
y
h 

A Completely Submerged Rectangular Flat Plate
Consider a completely submerged
rectangular plate of height “a” and
width “b” at an angle  from the
horizontal and whose top edge is
horizontal at a distance S from the
free surface along the plane of the
plate (see the shown figure). The
effect of Patm. Is assumed to be
= 0 (gage)
)
b
a
(
sin
)
2
a
S
(
g
F 




 


22. 22
Arbitrary datum
A
B
 g h =  g Z
Surface
Z
h
hn
Hn-1
hi
Lamina stratification
P
 

23. 23
X
h
d
Free Surface
Piezometric Line Z
Fluid at rest

24. 24
 F increases as H increases ?
 decreases as H increases?
 is constant as H increases?
 T increases as H increases?
 T is constant as H increases?
y
ycp 
y
ycp 
True or False???

25. 25
Hydraulic I (20) Fluid Static Forces
Hydrostatic Force on a Curved Surface
D C
E B
A
FH
W1
W2
 Assume Patm=0 (gage) at the free
surface,
 The hydrostatic force on the surface
EA : is Fx
 The net vertical force on the curve
surface AB is: FV=W1+W2
To find the line of action of the
resultant force, balance the
momentum about some convenient
point

26. 26
Hydraulic I (21) Fluid Static Forces
Pressure on Curved Surface (free body)

D
B
C
yCp
FV(1)
FH
FV(2)
E
 
w
EA
EA
DE
g
Fx 










2

A
  w
ABE
area
BCDE
area
g
FV 


 
S

27. 27
Hydraulic I (22) Fluid Static Forces
Pressure on Curved Surface (free body)
 Determine the volume of fluid above the curved surfa
 Compute the weight of the volume above it,
 The magnitude of the vertical component of the resu
force is equal to the weight of the determined volume.
acts in line with the centroid of the volume,
 Draw a projection of the curved surface onto a vertica
plane and determine its height called “S”,

28. 28
Hydraulic I (23) Fluid Static Forces
Pressure on Curved Surface (free body)
 Determine the depth to the centroid of the projected a
=DE+(S/2), where DE is the depth to the top of the projected a
 Compute the magnitude of the horizontal component
the resultant force, FH =  g h- A =  g (DE+S/2)x(Sx w)
 Compute the depth to the line of action of the horizon
force,
h
A
I
h
h
cg
cp 


29. 29
Hydraulic I (24) Fluid Static Forces
Pressure on Curved Surface (free body)
 For regular rectangular cross-section,
Thus,
 Compute the resultant force,
h
A
I
h
h
cg
cp 

 
w
S
h
S
DA
g
A
h
g
FH 













12
2


2
2
V
H
R F
F
F 


30. 30
Hydraulic I (25) Fluid Static Forces
Pressure on Curved Surface (free body)
 Compute the angle of inclination of the resultant forc
relative to the horizontal.
Thus,
11- Show the resultant force acting on the curved surfac
in such a direction that its line of action passes throu
the center of curvature of the surface.
 
H
V F
F
1

 tan


31. 31
Hydraulic I (26) Fluid Static Forces
2.50 m
2.80 m
2. 0 m
water Oil Sg = 0.90
Support
Gate, 0.60 m wide
Hinge
Pressure on Plane Surface (free body)

32. 32
Hydraulic I (27) Fluid Static Forces
The figure shows a gate hinged at its bottom
hinged at its bottom and held by a simple support
at its top. The gate separates two fluids. Compute
 the net force on the gate due to the fluid on each
side, and
 Compute the force on the hinge and on the
support.
Pressure on Plane Surface (free body)

33. 33
Hydraulic I (28) Fluid Static Forces
2.50 m
2.80 m
2. 0 m
water Oil Sg = 0.90
Support
Gate, 0.60 m wide
Hinge “o”
F1
F2
Hcp (1)
Hcp (1)
2.50 m
Pressure on Plane Surface (free body)

34. 34

35. 35
Grand Coulee Dam - Columbia River

36. 36
What are the magnitude and direction of the
force on the vertical rectangular dam (the shown
figure) of height H and width, w, due to
hydrostatic loads, and
 At what elevation is the center of pressure?

37. 37
Hydrostatic forces on a vertical dam face

38. 38
Because the area is (Hxw), the magnitude of the force,
2
H
w
g
2
1
A
h
g
F 
 

The center of pressure is found using, )
h
A
/(
I
h
y cg
p
.
c 
 12
/
H
w
I 3
cg 
Thus, 6
/
H
)
2
/
wH
(
)
12
/
H
w
(
h
y 2
3
p
.
c 


The hydrostatic pressure is , where is the dept
which the centroid of the dam is located.
h
g
P 
 2
H
h 

39. 39
The direction of the force is normal and compressive to the dam face a
shown .
The center of pressure is therefore located at a distance H/6 directly b
the centroid of the dam, or a distance 2H / 3 of below the water surfac

40. 40
 What is the net horizontal force acting on a
constant radius arch-dam face due to
hydrostatic forces?

41. 41

42. 42
The projected area is , while
H
sin
R
2
A projected 
 
The pressure at the centroid of the projected surface is h
g
P 

The magnitude of the horizontal force is thus
and the center of pressure lies below the water surface on the
line of symmetry of the dam face.


 sin
R
H
g
A
h
g
F 2


3
2 /
H
Because the face is assumed vertical, the vertical force on the dam is ze

43. 43
Radial Gate

44. 44

45. 45

46. 46
Worked Example
Hydrostatic Forces
H.I.T May 2010

47. 47
9.0 m
45 m
Wate
r
 Water Surface
9.0 m
A semicircular 9.0 m diameter tunnel is to be built under a 45
m deep, 240 m long lake, as shown. Determine the total
hydrostatic force acting on the roof of the tunnel.
Tunnel
Worked Example

48. 48
9.0 m
45 m
Water
 W
ater Surface
9.0 m
Tunnel
A
B C
D
E
Fx
Fy
Fx
Fy
The hydrostaticforce actingon the roof of the tunnel
The hydrostatic force acting on the roof of the tunnel

49. 49
The vertical force
 It acts vertically downward (see the shown figure below).
0

 x
F
  l
AED
area
ABCD
area
g
Fy 

 
kN
3
2
10
64
874
240
9
8
9
45
81
9
1000 













 .
.
