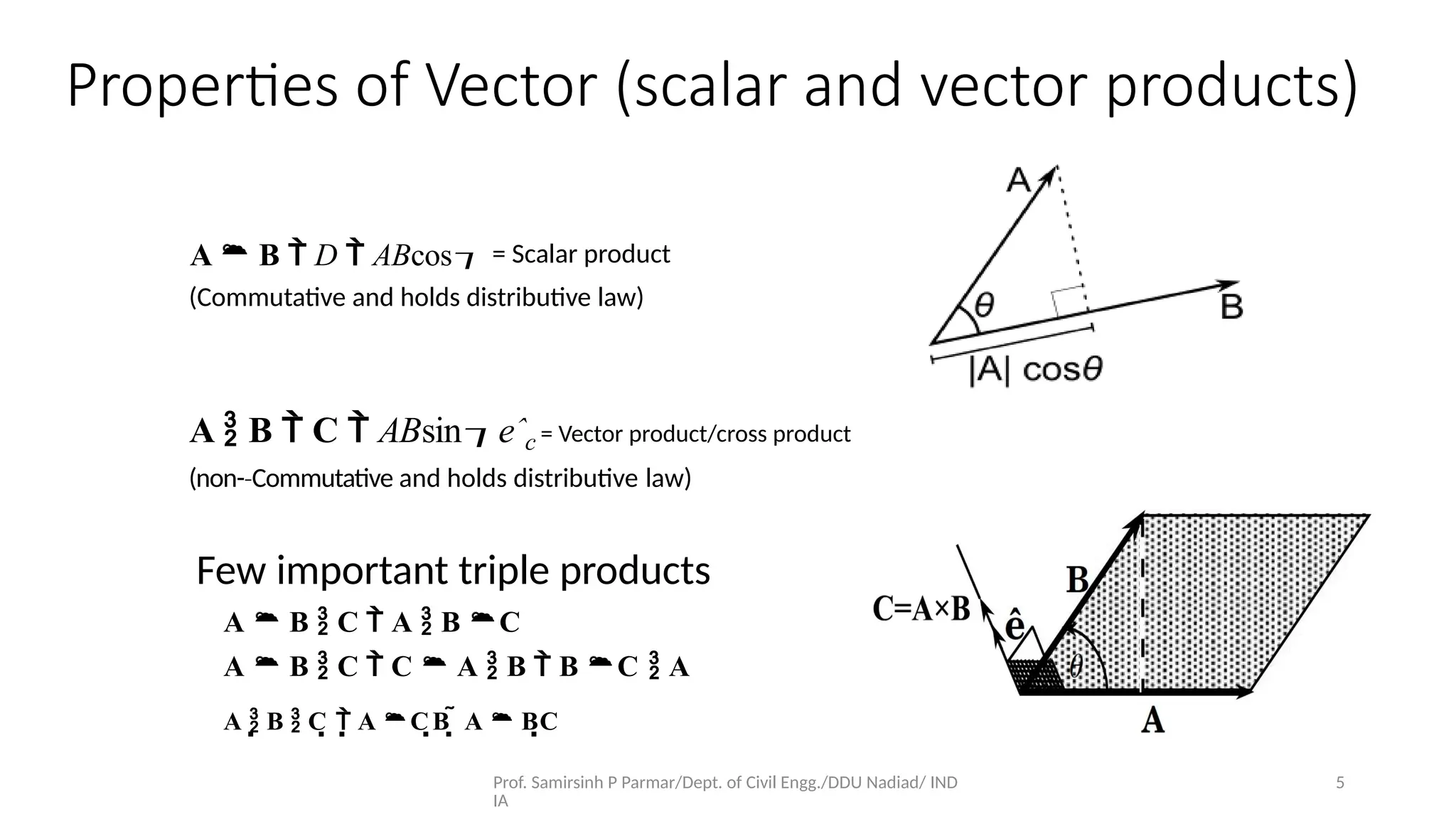
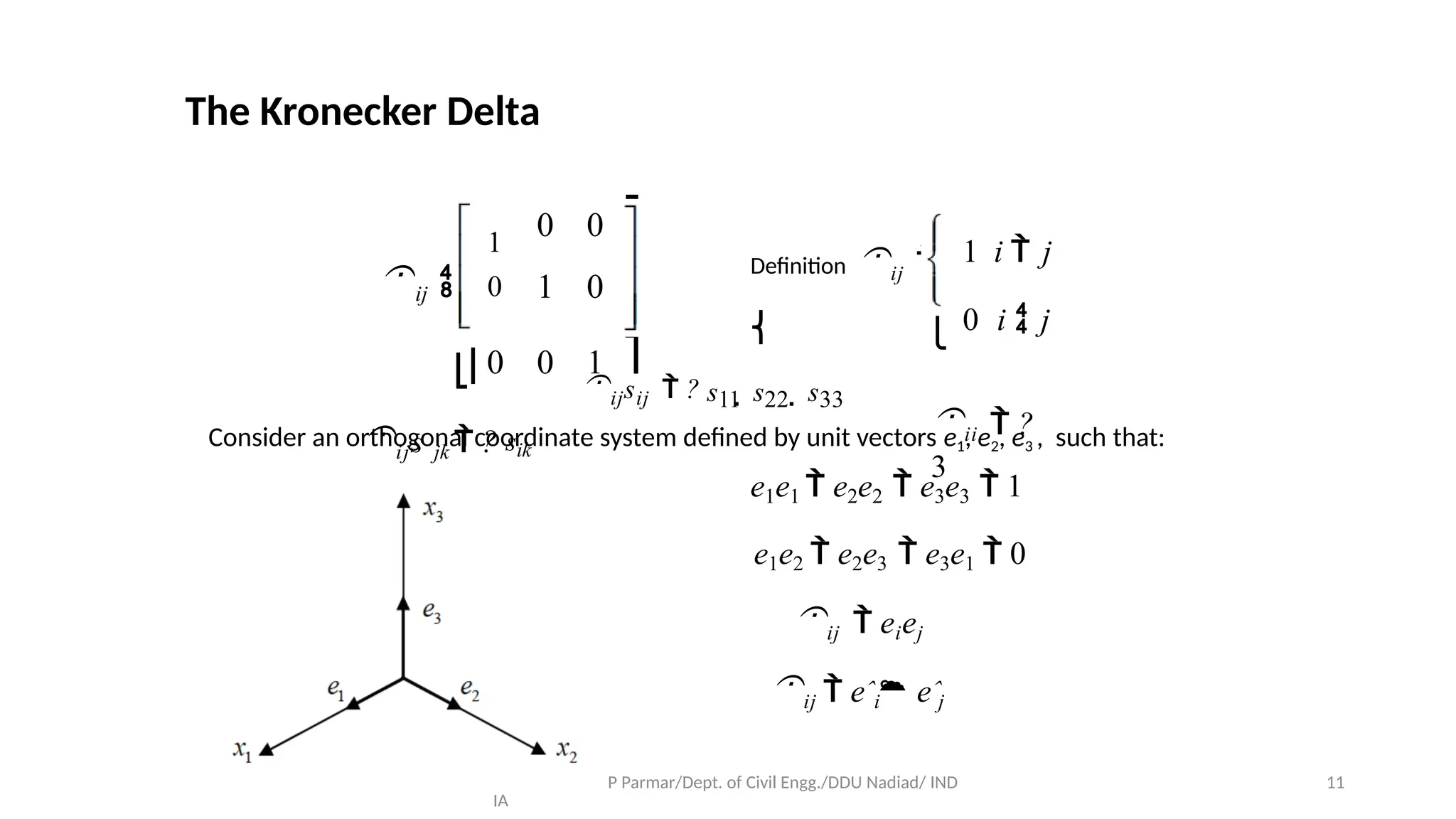
The document discusses tensor algebra and its applications in continuum mechanics, focusing on vector properties, scalar and vector fields, and matrix operations using index notation. It elaborates on the concepts of vectors, tensors, and their mathematical representations, including gradient, divergence, and curl. The content is intended for academic purposes and encourages the free distribution of knowledge.

1. Constitutive Modelling of
Geomaterials
Prof. Samirsinh P Parmar
Mail: samirddu@gmail.com
Asst. Prof. Department of Civil Engineering,
Faculty of Technology,
Dharmasinh Desai University, Nadiad, Gujarat, INDIA
Lecture: 3 : Tensor algebra and its application in continuum mechanics

2. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
2
2. Tensor algebra and its application in
continuum mechanics

3. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
3
Vector: recapitulation
Any quantity which encountered in analytical description of physical
phenomena, have magnitude and direction
and satisfy the parallelogram law of addition known as vector
Where
eˆ1,eˆ2 ,eˆ3
are the independent orthogonal unit vectors (base vectors)
and (A1, A2, A3) are the scalar component of A relative to the
base vectors
unit vector along A
Magnitude of A Cartesian basis
A

4. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
4
Properties of Vector (Addition)
(1)A + B = B + A (commutative).
(2)(A + B) + C = A + (B + C) (associative).
(3)A + 0 = A (existence of zero vector).
(4)A + (−A) = 0 (existence of negative vector).
Properties of Vector (scalar multiplication)
(5)α(βA) = (αβ)A (associative).
(6)(α + β)A = αA + βA (distributive scalar addition).
(7)α(A + B) = αA + αB (distributive vector addition). (4) 1A = A 
 1 = A, 0 
 A = 0.
Properties of Vector (Linear Independence)
(8)β1A1 + β2A2 + …+βnAn = 0 (A1, A2… An) are the linearly dependent
(9)β1A1 + β2A2 + …+βnAn ≠ 0 (A1, A2… An) are the linearly independent
(10)If (A1, A2) are the linearly dependent, they called collinear
(11)If (A1, A2, A3) are the linearly dependent, they called coplanar

5. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
5
Properties of Vector (scalar and vector products)
A  B  D  ABcos = Scalar product
(Commutative and holds distributive law)
A  B  C  ABsineˆc = Vector product/cross product
(non-­Commutative
‐ and holds distributive law)
Few important triple products
A  B  C  A  B C
A  B  C  C  A  B  B C  A
A  B  C  A CB  A  BC

6. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
6
Change of basis

7. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
7
Vector calculus Scalar field
r  x1eˆ1 x2eˆ2  x3eˆ3 denote the position vector of a point in space.
• A scalar field is a scalar valued function of position in space.
• A scalar field is a function of the components of the position vector, and so
may be expressed as φ (x1, x2, x3).
• The value of φ at a particular point in space must be independent of the
choice of basis vectors.
• e.g. temperature distribution throughout space, the pressure distribution in a
fluid
Vector field
• A vector field is a vector valued function of position in space.
• A vector field is a function of the components of the position vector, and so
may be expressed as
• v (x1, x2, x3)
• v = v1( x1, x2 , x3)ˆe1 + v2( x1, x2 , x3)ˆe2 + v3(x1, x2 , x3)ˆe3
• e.g. the speed and direction of a moving fluid throughout space, or the
strength and direction of some force, such as the magnetic or gravitational
force, as it changes from point to point.

8. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
8
Vector calculus
1

 2

3
grad   eˆ1
x
 eˆ2
x
 eˆ3
x

  
  eˆ1
x
 eˆ2
x

 eˆ3
x
1 2 3
Divergence of a vector field
div v 
v1 
v2 
v3
x1 x2 x3
Curl of a vector field
slope of the
tangent of the
graph of the
function
magnitude of a
vector field's
source or sink at a
given point
infinitesimal
rotation of a
3D vector field
Gradient of scalar field

9. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
9
MATRIX
Operations on Cartesian components of vectors and tensors may be expressed very efficiently and
clearly using index notation.
Lower case Latin subscripts (i, j, k…) have the range (1,2,3) Components of the
vector A are, A1, A2, A3
⎧
A1
⎫
⎪
⎪
A  Ai  ⎨ A2
⎬
⎪
S11 S12 S13
S22
S23
S32
S33
⎡
⎣
⎢
S  Sij  ⎢ S21
⎢ S31
⎤
⎥
⎥
⎥
⎦
A coordinate-­free,
‐ or component-­free
‐ , treatment of a scientific theory or mathematical topic
develops its concepts on any form of manifold without reference to any particular coordinate
system… Wikipedia
Indicial notation

10. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
10
i
1
3
L   Ai Bi  A1B1  A2 B2  A3B3  Ai Bi
Dummy and free index
The repeated index is called a dummy index because it can be replaced by any other symbol that has not already
been used in that expression
L  Ai Bi  Aj Bj  Ak Bk
Summation convention (Einstein convention)
If an index is repeated in a product of vectors or tensors, summation is implied over the repeated
index.
i
1
3 S11x1  S21x2  S31x3
⎧
cj   Sij xi  ⎨ S12 x1  S22 x2  S32 x3
⎪
⎪
⎩
 Sij xi
3 3
L    Sij Sij
 ?
i 1 j 1
S13x1  S23x2  S33x3
3
c?   sijt jk  ?
j 1
cik  sijd jk  simdmk  sindnk
The same index
(subscript) may not
appear more than
twice in a product of
two (or more)
vectors or tensors
ii
s  ?

11. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
11
The Kronecker Delta
⎡ 1
ij  ⎢ 0
⎤
⎥
⎥
⎦
⎥
Definition ij 
⎨
⎧ 1 i  j
⎩ 0 i  j
ii  ?
3
0 0
⎢
1 0
⎣⎢0 0 1
ijs jk  ? sik
ijsij  ? s11  s22  s33
Consider an orthogonal coordinate system defined by unit vectors e1, e2, e3 , such that:
e1e1  e2e2  e3e3  1
e1e2  e2e3  e3e1  0
ij  eiej
ij  eˆi eˆj

12. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
12
The Permutation (alternating tensor) Symbol
1 if i, j, k in cyclic order and not repeated
1 if i, j, k not in cyclic order and not
repeated
0 otherwise
⎧
⎪
⎩
eijk  ⎨
⎪
eˆi eˆ
j  eijk eˆk
In an orthonormal basis, the scalar and vector products can be expressed in the
index form using the Kronecker delta and the alternating symbols:
A  B   Aieˆi    Bj eˆj   Ai Bjij  Ai Bi
A  B   Aieˆi    Bj eˆj   Ai Bj eijk eˆk
eijk eimn   jm kn  
jn km
(e-­
‐δ
identity)

13. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
13
Partial differentiation is denoted by a comma followed by the index of differentiation.
Notation for partial differentiation
 f
f,i 
x i
and
x j,i 
xj
xi
Now if f(xi)
f,i 
x
 f  f x1  f x2
i 1 i 2 i 3
 f x3
  
x x x x x
x
i
 f, j x j,i
where i = free index and j = dummy index
xi
x j


ij
Qij
Qkl
 

ik jl

14. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
14
Tensor
A mathematical object analogous to but more general than a vector, represented by an
array of components that are functions of the coordinates of a space… (Wikipedia)
Tensors are a further extension of ideas we already use when defining quantities like
scalars and vectors.
stress =
force Magnitude and direction
area Orientation of plane
Complete definition of Stress must include its type, either tensile/compressive or shear.
Thus, specification of stress at a point requires two vectors, one perpendicular to the
plane on which the force is acting and the other in the direction of the force. Such an
object is known as a dyad, or what we shall call a second-­order
‐ tensor.

15. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
15
Tensor
A linear operator that transforms a vector or a tensor to another vector or tensor.
Change of basis in index notation i  Qij Aj
Qij  i Aj
Q =   
Qij (transformation matrix) is a second order tensor
Creation of a second order tensor from the product of two vectors
also known as dyadic product
Index notation
Tensor notation
Gradient of a vector field another example of dyadic product to create
tensor grad v    v

16. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
16
The rank (or order) of a tensor is defined by the number of directions (and hence the
dimensionality of the array) required to describe it.
Order of tensor

17. Prof. Samirsinh P Parmar/Dept. of Civil Engg./DDU Nadiad/ IND
IA
17
References:
Wikipedia: continuum mechanics/stress/strain…

18. Disclaimer
• The purpose of publishing this “ PPT” is fully academic.
Publisher does not want any credit or copyright on it. You
can download it , modify it, print it, distribute it for academic
purpose.
• Knowledge increases by distributing it, hence please do not
involve yourself in “ Knowledge Blockade” nuisance in
academic industry.
• Before thinking of copyright just think @ the things we use
in routine which we are using freely, without copyright.
• Man may die- does not knowledge.
• Jurisdiction is limited to Godhra, Panchmahals, Gujarat,

19. Any Questions ?
Thank You