vector and tensor

1. Transport Phenomena
Introduction
By
Dr Sourav Poddar
Department of Chemical Engineering
National Institute of Technology, Tiruchirappalli

4. • Vector and Tensor Analysis
• Momentum Transport
• Heat Transfer
• Mass Transport

5. Vector and Tensor Analysis
Introduction
Transport Phenomena is the subject which deals with the movement of different physical quantities in any chemical
or mechanical process and describes the basic principles and laws of transport. It also describes the relations and
similarities among different types of transport that may occur in any system. Transport in a chemical or mechanical
process can be classified into three types:
1. Momentum transport deals with the transport of momentum in fluids and is also known as fluid dynamics.
2. Energy transport deals with the transport of different forms of energy in a system and is also known as heat
transfer.
3.Mass transport deals with the transport of various chemical species themselves.

6. Three different types of physical quantities are used in transport phenomena: scalars
(e.g. temperature, pressure and concentration), vectors (e.g. velocity, momentum and
force) and second order tensors (e.g. stress or momentum flux and velocity gradient). It
is essential to have a primary knowledge of the mathematical operations of scalar,
vector and tensor quantities for solving the problems of transport phenomena. In fact,
the use of the indicial notation in cartesian coordinates will enable us to express the
long formulae encountered in transport phenomena in a concise and compact fashion.
In addition, any equation written in vector tensor form is equally valid in any
coordinate system.

7. In this course, we will be using the following notations for scalar, vector and tensor quantities:
notations:
a, b, c scalar quantities
vector quantities
2nd order tensor quantities
Cartesian coordinates and unit vectors
A xyz cartesian coordinate system may also be conventionally written as shown in Fig.1.1 below.
Fig. 1.1 3-dimensional cartesian coordinate system with unit vector
Here, and are the unit vectors in x, y and z direction respectively.

8. Tensor quantities
Most of us might have already encountered scalars and vectors in the study of high-school physics. It was pointed
out that the vectors also have a direction associated with them along with a magnitude, whereas scalars only have
a magnitude but no direction. Extending this definition, we can loosely define a 2nd order tensor as a physical
quantity which has a magnitude and two different directions associated with it. To better understand, why we
might need two different directions for specifying a particular physical quantity. Let us take the example of the
stresses which may arise in a solid body, or in a fluid. Clearly, the stresses are associated with magnitude of forces,
as well as with an area, whose direction is also need to be specified by the outward normal to the face of the area
on which a particular force acting. Hence, we will require 32, i.e., 9 components to specify a stress completely in a
3 dimensional cartesian coordinate system. In general, an nth order tensor will be specified by 3n components (in a
3-dimensional system). However, the number of components alone cannot determine whether a physical quantity
is a vector or a tensor. The additional requirement is that there should be some transformation rule for obtaining
the corresponding tensors when we rotate the coordinate system about the origin. Thus, the tensor quantities can
be defined by two essential conditions:

9. 1. These quantities should have 3n components. According to this
definition, scalar quantities are zero order tensors and have 30=
1 component. Vector quantities are first order tensors and have 31 =
3 components. Second order tensors have 32 = 9 components and
third order tensors have 33 = 27 components. Third and higher order
tensors are not used in transport phenomena, and are not dealt here.
2. The second necessary requirement of any tensor quantity is that it
should follow some transformation rule.

10. Kronecker delta & Alternating Unit Tensor
There are two quantities which are quite useful in conveniently and concisely expressing several mathematical
operations on tensors. These are the Kronecker delta and the alternating unit tensor.
Kronecker delta
Kronecker delta or Kronecker’s delta is a function of two index variables, usually integer, which is 1 if they
are equal and 0 otherwise.
It is expressed as a symbol δij
δij=1, if i=j
δij=0, if i≠j
Thus, in three dimensions, we may also express the Kronecker delta in matrix form

11. Alternating unit tensor
The alternating unit tensor εijk is useful when expressing certain results in a compact form in index notation. It
may be noted that the alternating unit tensor has three index and therefore 27 possible combinations but it is a
scalar quantity
• εijk= 0 if any two of indices i, j, k are equal. For example ε113,ε131,ε111,ε222=0
• εijk= +1 when the indices i, j, k are different and are in cyclic order (123), For example ε123
 εijk=-1 when the indices i, j, k are different and are in anti-cyclic order. For example ε321

12. Free indices and Dummy indices
Free indices
Free indices are the indices which occur only once in each tensor term. For example, i is the free index in
following expression vij wj
In any tensorial equation, every term should have an equal number of free indices. For example, vij wj =cj dj is not
a valid tensorial expression since the number of free indices (index i) is not equal in both terms.
Any free indices in a tensorial expression can be replaced by any other indices as long as this symbol has not
already occurred in the expression. For example, Aij Bj= CiDjEj is equivalent to Akj Bj= CkDjEj
The number of free indices in an equation gives the actual number of mathematical equations that will arise from
it. For example, in equation Aij Bj= CiDjEj corresponds to 31 = 3 equations since there is only one free
indices i. It may be noted that each indices can take value i=1, 2 or 3.

13. Dummy indices
Dummy indices are the indices that occur twice in a tensor term. For example, j is the dummy
index in Aij Bj.
Any dummy index implies the summation of all components of that tensor term associated with
each coordinate axis. Thus, when we write Aiδi, we actually imply
Any dummy index in a tensor term can be replaced by any other symbol as long as this
symbol has not already occurred in previous terms. For example, Aijkδjδk= Aipqδpδq.
Note: The dummy indices can be renamed in each term separately in a equations but free indices should be
renamed for all terms in a tensor equations. For example, Aij Bj= CiDjEj can be replaced by Akp Bp= CkDjEj.
Here, i is the free index which has been replaced by k in both terms but j is a dummy index and can be replaced
either in one term or both.

14. Summation convention in vector and tensor analysis
According to the summation convention rule, if k is a dummy index
which repeats itself in a term then there should be a summation sign
associated with it. Therefore, we can eliminate the implied summation
sign and can write the expression in a more compact way. For example,
using the summation convention
can be simply written as εijkεljk . Since j and k are repeating, there is no need to
write summation sign over these indices

15. Relation between alternating unit tensor and Kronecker delta
When two indices are common between the two alternating unit tensors, that the following can be shown easily
.......................................................................(2.1)
When one index is common between the two alternating unit tensors, there product may be written as
.......................................................................(2.2)

16. 16
Mathematics Review
A.1 Vectors
A.1.1 Definitions
A.1.2 Products
A.1.2.1 Scalar Products A.1.2.2 Vector Product
V．W = ｜v｜ ｜W｜cos(V,W)
= vxwx + vywy + vzwz
V x W = ｜v｜｜W｜sin(V,W) nvw
V = vx ex + vyey + vzez
ex ey ez
vx vy vz
wx wy wz
=

19. (b) Divergence of vector field
Dot product of the del operator and a vector quantity is called the divergence
of vector field. It is a scalar quantity. If is a vector quantity then
divergence of a vector field is

24. 24
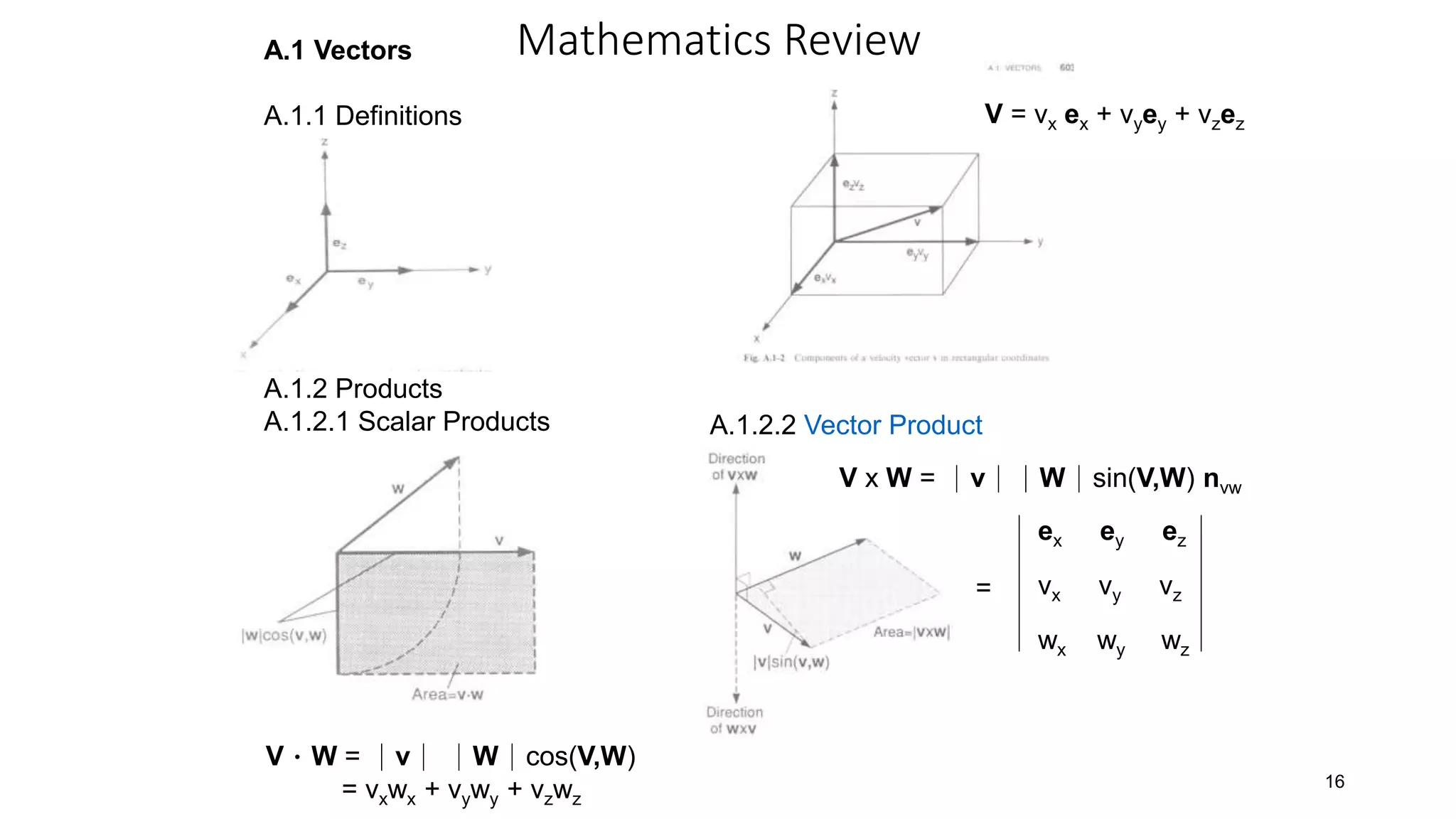
A.2 Tensors
A.2.1 Definitions
A tensor (2nd order) has nine components, for example, a stress tensor
can be expressed in rectangular coordinates listed in the following:
A.2.2 Product
The tensor product of two vectors v and w, denoted as vw, is a tensor defined by
xx xy xz
yx yy yz
zx zy zz
  
  
  
 
 
  
 
 
τ
 
x x x x y x z
y x y z y x y y y z
z x z y z z
z
v v w v w v w
v w w w v w v w v w
v w v w v w
v
   
   
 
   
 
 
 
 
vw
[A.2-1]
[A.2-2]
Explanation (Borisenko, p64)

25. 25
The vector product of a tensor  and a vector v, denoted by ．v is a vector defined by
   
 
x
xx xy xz
yx yy yz y
zx zy zz z
x xx y xy z xz x yx y yy z yz
x zx y zy z zz
x y
z
v
v v
v
v v v v v v
v v v
  
  
  
     
  
 
 
 
 
   
 
   
   
     
  
τ
e e
e
[A.2-3]
   
 
  
 
x
x x x y x z
y x y y y z y
z x z y z z z
x x x x y y x z z y x x y y y y z z
z x x z y y z z z
x y z x x y y z z
x y
z
x y z
n
v v v v v v
v v v v v v n
v v v v v v n
v v n v v n v v n v v n v v n v v n
v v n v v n v v n
v v v v n v n v n
 
 
 
 
   
 
   
   
     
  
    
 
vv n
e e
e
e e e
v v n [A.2-5]
The product between a tensor vv and a vector n is a vector

26. 26
The scalar product of two tensors s and , denoted as s:, is a scalar defined by
: :
xx xy xz xx xy xz
yx yy yz yx yy yz
zx zy zz zx zy zz
xx xx xy yx xz zx yx xy yy yy yz zy
zx xz zy yz zz zz
s s s   
s s s   
s s s   
s  s  s  s  s  s 
s  s  s 
   
   
    
   
   
     
  
σ τ
[A.2-6]
: :
x x x y x z xx xy xz
y x y y y z yx yy yz
z x z y z z zx zy zz
x x xx x y yx x z zx y x xy y y yy y z zy
z x xz z y yz z z zz
v w v w v w
v w v w v w
v w v w v w
v w v w v w v w v w v w
v w v w v w
  
   
  
     
  
   
   
    
   
   
     
  
vw [A.2-7]
The scalar product of two tensors vw and  is
Physical quantity Multiplication sign
Scalar Vector Tensor None X ‧ :
Order 0 1 2 0 -1 -2 -4
Table A.1-1 Orders of physical quantities and their multiplication signs

27. 2
x y z
x y z
  
   
  
e e e
x y z
s s s
s
x y z
  
   
  
e e e
A.3 Differential Operators
A.3.1 Definitions
The vector differential operation , called “del”, has components similar to those
of a vector. However, unlike a vector, it cannot stand alone and must operate on
a scalar, vector, or tensor function. In rectangular coordinates it is defined by
The gradient of a scalar field s, denoted as ▽ s, is a vector defined by
[A.3-1]
[A.3-2]
A.3.2 Products
The divergence of a vector field v, denoted as ▽‧v is a scalar .
[A.3-5]
 
v x y z x x y y z z
x y z
v v v
x y z
v v v
x y z
 
  
      
 
  
 
  
  
  
e e e e e e
Flux is defined as the amount that flows through a unit area per unit time
Flow rate is the volume of fluid which passes through a given surface per unit time

28. 28
   
     
x y z x x y y z z
x y z
x y z
x y z
a av av av
x y z
av av av
x y z
v v v a a a
a v v v
x y z x y z
 
  
      
 
  
 
  
  
  
   
     
     
   
     
   
v e e e e e e
Similarly
[A.3-5]
For the operation of [A.3-7]
   
a a a
    
v v v
For the operation of ▽‧▽s, we have
[A.3-8]
[A.3-9]
2
2
2
2
2
2
)
e
e
e
(
)
e
e
e
(
z
s
y
s
x
s
z
s
y
s
x
s
z
y
x
s z
y
x
z
y
x






























In other words s
s 2





Where the differential operator▽2, called Laplace operator, is defined as
2
2
2
2
2
2
2
z
y
x 








 [A.3-10]
For example: Streamline is defined as a line everywhere tangent to the velocity
vector at a given instant and can be described as a scale function of f.
Lines of constant f are streamlines of the flow for inviscid irrotational flow
in the xy plane ▽2f=0

29. 29
x y z
x y z
e e e
x y z
v v v
  
 
  
v
 
x y z
x y z
x y z
x y z
v v v
x x x x
v v v
v v v
y y y y
v v v
z z z z
   
   
   
   
   
   
   
  
   
   
   
   
   
   
   
   
v
The curl of a vector field v, denoted by ▽ x v, is a vector like the vector product
of two vectors.
[A.3-11]
[A.3-12]
Like the tensor product of two vectors, ▽v is a tensor as shown:
x y x z y x
x y z
v v v v v v
e e e
y z z x x y
   
     
 
     
   
 
     
 
   
When the flow is irrotational, v = 0


30. 30
[A.3-13]
Like the vector product of a vector and a tensor, ▽‧ is a vector.
xx xy xz
yx yy yz
zx zy zz
yx xy yy zy
xx zx
yz
xz zz
x y
z
x y z
x y z x y z
x y z
  
  
  
   
 

 
 
 
    
  
   
  
   
 
   
   
 
     
   
     
   

 
 
  
 
  
 
τ
e e
e
 
     
     
     
x x x y x z
y x y y y z
z x z y z z
x x x y x z x
y x y y y z y
z x z y z z z
v v v v v v
v v v v v v
x y z
v v v v v v
v v v v v v
x y z
v v v v v v
x y z
v v v v v v
x y z
  
   
  
  
  
  
 
 
    
  
   
  
   
 
 
  
  
 
  
 
 
  
  
 
  
 
 
  
  
 
  
 
vv
e
e
e
[A.3-14]
From Eq. [A.2-2]
[A.3-15]
It can be shown that    
  
    
vv v v v v

63. Second order tensor
Analogous to a vector, second order tensor must also follow some transformation rules. Firstly,
they should contain 32
= 9 components and secondly, they should also follow the following
transformation rule as follows.
if m=1 and n=1 then, and from Equation (4.1), we have
,
For a second order tensor, are the normal components of the tensor and this
second order tensor is symmetric, if

64. 2nd order tensor as dyadic product of two vectors
As we have discussed earlier, the dyadic product of two vectors is a 2nd
order tensor quantity.
For example, if and are two vectors, then
From Equation 4.6, we can see that on the right hand side nine terms have been added together
and if we omit the product of unit vectors, the nine components may written as shown below
Thus,

65. Mathematical operations for 2nd order tensors
The following mathematical operations are possible for 2nd order tensor quantities
Addition of 2nd order tensors
Tensors of the same order can be added or subtracted as follows
Similarly,

66. Multiplication of tensors
Various multiplication operations are possible between two different order tensors. Some of
these are shown below
Multiplication of a 2nd order tensor by a scalar
A scalar and a 2nd
order tensor quantity can be multiplied as follows
Multiplication of a 2nd order tensor by a vector
A vector and a 2nd
order tensor can be multiplied in various ways:

67. 1. Dyadic product of a vector and 2nd order tensor
Dyadic product of vector and tensor is a third order tensor. Though, it is not required in
transport phenomena, may still be computed as shown below
2. Dot product of a vector and a 2nd order tensor
Dot operation reduces the order of resulting quantity by two. Hence, the dot product of a vector
and a tensor is a vector quantity. For example, if is a 2nd tensor and is a vector
quantity, then

68. Next, we perform the dot operation between two the nearest unit vectors as shown below
replace j by k or k by j
thus
For example, if i = 1, then

70. Dyadic Product of two tensors Dyadic product of two second order tensors is a fourth order
tensor quantity. It is not discussed here as this is not required in transport phenomena. Cross
product of two tensors Cross product of two second order tensors is a third order tensor
quantity and is not discussed here for the same reason as above.

71. Dot product of tensors (tensor product) Dot reduces the order of resultant quantity by two.
Thus, the dot product of two second order tensors is a second order tensor quantity.
If and are two second order tensors, then
While performing the dot product between two-unit vectors, the order in which indices
appear above, should not be changed and the dot product should be performed between the
two nearest unit vectors. Replace k by j (or you may also replace j by k) (compaction
operation)

72. Double dot product or Scalar product of two second order tensors Double dot operation
reduces the order of resultant quantity by four. Thus, the double dot product of two second
order tensors is a scalar quantity. If and are two second order tensors, then. First
dot operation should take place between the two nearer vectors and the next dot operation
should take place between two remaining unit vectors.
Hence, (Replace k by j)
(Replace l by i)
which is a scalar quantity.

73. 73
A.4 Divergence Theorem
A.4.1 Vectors
Let Ω be a closed region in space surrounded by a surface A and n the outward-
directed unit vector normal to the surface. For a vector v
A
d dA

   
 
v v n [A.4-1]
This equation , called the gauss divergence theorem, is useful for converting from a
surface integral to a volume integral.
A.4.2 Scalars
A.4.3 Tensors
For a scale s
For a tensor  or vv
A
sd s dA

  
  n
   
A
d dA
 

   
  n
   
A
d dA

   
 
vv vv n
[A.4-2]
[A.4-3]
[A.4-4]

80. Time derivatives in transport phenomena Many times, we are interested to know how fast any
physical quantity or property is changing with time. However, the property might be also the
function of space coordinates, makes more complicated to measure. In this section, three
different types of time derivatives are discussed.
1. Partial derivative, denoted as
2. Total derivative, denoted as
3. Substantial derivative, denoted as

81. To understand the differences between these time derivatives, let us consider a hypothetical
case. A chimney produces flue gases containing SO2 and we want to study the change in
SO2 concentration with time.
Fig 6.1 Partial derivative with constant observer at point C

82. Partial derivative If the observer remains fixed at a particular position and determines the
change in the concentration of SO2. It is being the partial derivative that is measured. At
time t=t, let the concentration of SO2 be C1 and at time t+Δt, let it be C1+ΔC1. Thus, the time
derivative, which is the measure of change in SO2 concentration is given by
While calculating the partial derivative it is assumed other space coordinates remain
constant. Total derivative If, however, the observer also changes his position with time. It is
the total derivative which is measured. Suppose at any time t = t, the observer is situated at
the point A and measures concentration of SO2 as C1. At time t= t+Δt, the observer has move
and reaches a different location at point B. Let this measured concentration of of SO2 be C2 .
In this case, the time derivative
is
This may be called a total derivative as the change in concentration with respect to both time
and space is being considered. Therefore, it should also include the effects of the velocity of
observer. Mathematically this time derivative may be expressed
as,

83. Here, ux, uy and uz are the components of the velocity of the observer in
the x, y and z directions respectively. Substantial derivative It is a special case of the total
derivative where the observer floats in a balloon with the speed of the air around it. Thus, the
velocity of fluid is same as the velocity of the observer. In this
case,
where vx, vy and vz are the components of the velocity of the fluid. To understand the
differences between partial and substantial derivatives, let us take a simple one dimensional
problem. Let the point A be at the position ‘x’, and point B be at the position ‘x+ Δx’. The
concentration of SO2 is a function of both time t as well as spatial coordinate x. As shown in
Figure 6.2, the concentration profile (plot of C vs. x) changes with time. Let the concentration
of SO2 at the point A be recorded at time t=t as C1 and at time t+Δt as C2. In the same way,
the concentration of SO2 is recorded at point B at time t=t as C3 and at time t=t+Δt as C4 as
shown in Fig. 6.2

84. Fig 6.2 Position of observer A ( C1 & C2 ) and B ( C3 and C4 )
The observer, starting from point A, reaches the point B in time Δt . If the velocity of the
observer is ux , the distance traversed in time Δt will be Δx=ux Δt The partial derivatives can
thus be computed
as
The substantial derivative, is however computed
as

85. Equation (6.7) shows the difference between the partial and the substantial derivative. In
order to relate the two mathematically, we may proceed as follows. From the Fig. 6.2, C3 may
be written
as
Furthermore, C4 can be written in terms of C3 as
Therefore,
Dividing the equation by Δt and taking the limit as Δt → 0, we have

86. Generalizing the Equation (6.4) and making it independent of the coordinate system, we may
write it in vector and tensor form
as
The above definition of substantial derivative may also apply to a quantity which is vector or
second order tensor,
i.e.,

87. 87
A.5 Curvilinear Coordinates
For many problems in transport phenomena, the curvilinear coordinates such as
cylindrical and spherical coordinates are more natural than rectangular coordinates.
A point P in space, as shown in Fig. A.5.1, can be represented by P(x,y,z) in
rectangular coordinates, P(r, θ,z) in cylindrical coordinates, or P(r, θ,ψ) in
spherical coordinates.
Fig. A.5-1(a)
A.5.1 Cartesian Coordinates
For Cartesian coordinates, as shown
in A.5-1(a), the differential increments
of a control unit in x, y and z axis are
dx, dy , and dz, respectively.
x
y
z
dx
dy
dz
P(x,y,z) ex
ey
ez

88. 88
Fig. A.5-1(b)
A.5.1 Cylindrical Coordinates
For cylindrical coordinates, as shown in A.5-1(b), the variables r, θ, and z are
related to x, y, and z.
x = r cosθ [A.5-1] y = r sinθ [A.5-2] z = z [A.5-3]
Fig. A.5-1(b)*
v = er vr + eθvθ + ezvz
rr r rz
r z
zr z zz

  

  
  
  
 
 
  
 
 
τ
and
The differential increments of a control unit, as shown in Fig. A.5-1(b)*, in r, ,
and z axis are dr, rd , and dz, respectively. A vector v and a tensor τcan be
expressed as follows:

89. 89
Fig. A.5-1(c)
A.5.2 Spherical Coordinates
For spherical coordinates, as shown in A.5-1(c), the variables r, θ, and ψ are
related to x, y, and z as follows
x= r sin cosf A.5-6
y = r sin sinf [A.5-7]
z = r cos A.5-8
[A.5-9]
rr r rz
r z
zr z zz

  

  
  
  
 
 
  
 
 
τ [A.5-10]
The differential increments of a control
unit, as shown in Fig. A.5-1(c)*, in r, θ,
and φ axis are dr, rdθ , and rsinθdφ ,
respectively. A vector v and a tensor τ
can be expressed as follows:
f
f

 v
v
vr
r e
e
e
v 


Fig. A.5-1(c)*
θ
φ φ
θ
θ φ
θ
θ

90. 90
A.5.3 Differential Operators
1
0
0
rz
r z
zr z zz
r zr
rr r
r
r rr z
  




  
  
  
  
   
   
  
   
   
   
  
τ e
e e e
1
0
0
r
r
r
r r
rr r
r
r rr

  
  
 

 
  
  
  
  
   
   
  
   
 
 
 
 
  
τ e
e e e
1
r z
s s s
s
r r z


  
   
  
e e e
1 1
sin
r
s s s
s
r r r
 f
  f
  
   
  
e e e
Vectors, tensors, and their products in curvilinear coordinates are similar in form
to those in curvilinear coordinates. For example, if v = er in cylindrical coordinates,
the operation of τ．er can be expressed in [A.5-11], and it can be expressed in
[A.5-12] when in spherical coordinates
[A.5-11] [A.5-12]
In curvilinear coordinates, ▽ assumes different forms depending on the orders of
the physical quantities and the multiplication sign involved. For example, in cylindrical
coordinates
Whereas in spherical coordinates,
[A.5-13]
[A.5-14]

95. OR

97. Transfer processes

98. Transfer processes

99. Transfer processes

100. Transfer processes

101. Summary of transfer processes

104. Ratios of transport diffusivities

105. Ratios of transport diffusivities

106. Rapid and brief introduction to mass transfer

113. Turbulent mass diffusivities

114. Convective mass transfer

116. Convective mass transfer

118. Convective mass transfer correlations

119. Interphase mass transfer: Two film theory

120. Two-film theory: Overall mass transfer coefficient

121. Diffusion coefficient or mass diffusivity

122. Ranges of mass diffusivities

123. Diffusion coefficient or mass diffusivity

124. Experimental diffusion coefficients

125. Diffusion coefficient for gases at low pressure

126. Diffusion coefficient for gases at low pressure:
Estimation

129. Diffusion coefficient for gases at low pressure:
Estimation

131. Diffusion coefficient for gases at low pressure: Estimation

132. Lennard-Jones potential

133. Diffusion coefficient for gases at low pressure:
Estimation

134. Diffusion coefficient for gases at low
pressure: Estimation

137. Fuller’s equation

138. Diffusion volumes to be used with Fuller’s equation

140. Diffusion coefficient for gases at high density

141. Diffusion coefficient for gases at high density:
Takahashi method

143. Diffusion coefficient for gas mixtures

144. Diffusion coefficient for gas mixtures

145. Diffusion coefficient for gas mixtures

146. Diffusion coefficient for liquid mixtures

147. Diffusion coefficient for liquid mixtures

148. Selected molar volumes at normal boiling points

149. Atomic volumes for calculating molar volumes and corrections

150. Diffusion coefficient for liquid mixtures

151. Why do we need shell (small
control element ) mass
balance?

152. We need, because, we desire to know what
is happening inside. In other words, we
want to know the differential or point to
point molar flux and concentration
distributions with in a system, i.e., we will
represent the system in terms of
differential equations. Macro or bulk
balances such as that applied in material
balance calculations only give input and
output information and do not tell what
happens inside the system.

155. Coordinate systems

157. Diffusion through a
stagnant gas film

158. Diffusion through a stagnant gas film

159. Diffusion through a stagnant gas film

163. Diffusion through a stagnant gas film:
Concentration profile

164. Diffusion through a stagnant gas film:
Molar flux

165. Diffusion through a stagnant gas film

166. Pseudosteady state diffusion through a stagnant
gas film

167. Diffusion through a stagnant gas film:
Applications

168. Diffusion through a stagnant gas film: Defects

169. Diffusion of A through stagnant gas film in spherical
coordinates

170. Diffusion of A through stagnant gas film in
spherical coordinates

172. Diffusion of A through stagnant gas film in cylindrical
coordinates

174. Diffusion of A through Pyrex glass tube

176. Diffusion with a heterogeneous chemical reaction

193. Significance of dimensionless numbers
It is convenient to write the above mentioned differential
equations and their boundary conditions in terms of
dimensionless groups. Dimensionless groups may have smaller
numerical values which may facilitate a numerical solution. Also
analysis of the system may be described in a more convenient
manner.
The above equations are usually written in terms of Peclet
number

195. Solution of partial differential equations

199. Liquid pulsed extraction column

200. Mathematical modeling of a differential
extraction column

201. Mathematical modeling of a differential
extraction column

202. Differential equation for mass transfer

204. Differential equations for mass transfer in terms of NA
(molar units)

205. Differential equation for mass transfer in rectangular
coordinates (mass units)

206. Differential equations for mass transfer in terms of jAz

207. Differential equations for mass transfer in terms of ωA

211. THANK YOU