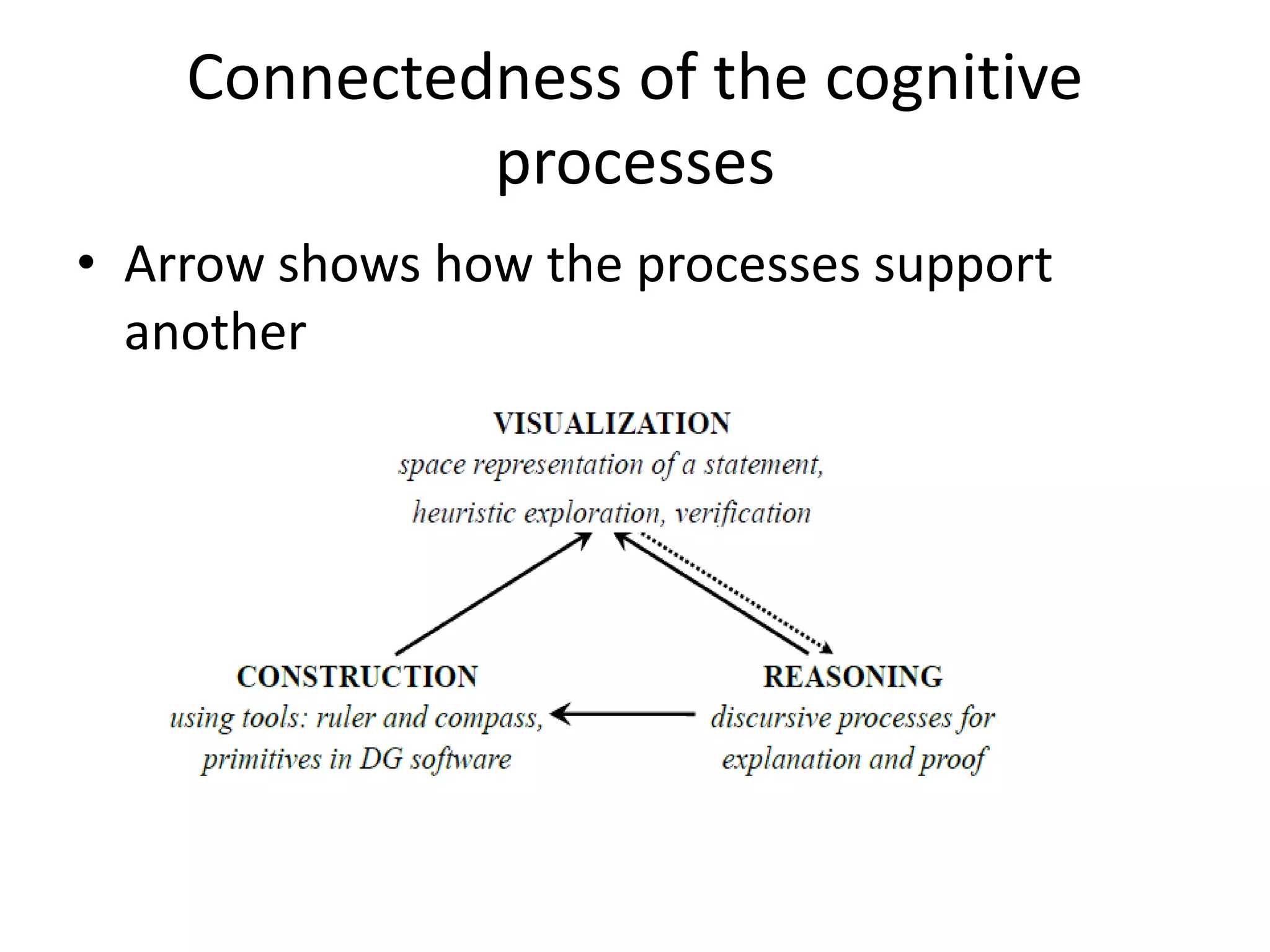
The document discusses the rationale for teaching geometry in schools. It outlines several key reasons: geometry teaches deductive reasoning skills, helps students develop spatial reasoning abilities, and provides a context for quantifying measurements of real-world objects. The document also reviews Duval's cognitive model of geometric reasoning, which identifies three processes - visualization, construction, and reasoning - that students use to understand geometric concepts. Duval's model examines how students apprehend geometric figures through perceptual, sequential, discursive, and operative processes in order to solve problems.

1. Teaching geometry

2. Rationale for teaching geometry
• geometry has been an integral part of mathematics and a common
vehicle for teaching the critical skill of deductive reasoning.
• It offers a physical context in which students can develop and refine
intuition, leading to the formulation and testing of hypotheses and
ultimately resulting in the justification of arguments, both formally
and informally. Geometry also describes changes in objects under
such transformations as translation, rotation, reflection, and dilation.
• It helps students understand the structure of space and the nature of
spatial relations.
• The measurement aspect of geometry provides a basis by which we
quantify the world.
• Solving practical problems relies to some extent on approximate
physical measurements but also rests on geometric properties that
are exact in nature.
• Grounded in such certainty, geometry provides an excellent medium
for the development of students’ ability to reason and produce
thoughtful, logical arguments

3. example
• -Concepts involved in FET Euclidean Geometry
• -Difficulties & limitations connected with
teaching Euclidean Geometry
• -Specific strategies and procedures for
teaching Euclidean Geometry)
• -barriers to understanding Euclidean
Geometry
• -teaching FET Euclidean Geometry with
technology (DGE)

4. • Several frameworks for geometrical reasoning were proposed by
research studies in the 1990’s that aimed at understanding the
processes of teaching and learning geometry.
1. Jones (1998) suggests the van Hiele’s (1986) model of thinking in
geometry,
2. Fischbein’s (1993) theory of figural concepts, and
3. Duval (1995) cognitive apprehensions for geometrical reasoning.
The van Hiele (1986) model is prominent among studies on geometry
knowledge in South Africa. For example van der Sandt (2007), van der
Sandt and Nieuwoudt (2005), Atebe (2008) and Luneta (2014) employed
the van Hiele model of geometry thinking to study geometry knowledge
at primary, secondary and tertiary education.
The Duval model is of particular interest as it is more concerned with
understanding the development of cognitive processes as revealed when
solving geometry problems (Duval, 1998, 2007). Duval (1995) suggests an
analytic theory for analysing thinking processes involved in a geometric
activity.

5. Learning and Teaching of Geometry:
three cognitive processes to identify reasons for why and how geometry
should be taught in school (Duval, 1995)
Visualization process : refers to the use of
representations (e.g figures, images, diagrams,
symbols) for illustration, exploration or
verification of different geometric situations;
Construction process: related to actions for
constructing a configuration according to
restricted tools and geometrical requirements;
Reasoning process: related to discursive
processes for proof and explanation.

6. Connectedness of the cognitive
processes
• Arrow shows how the processes support
another

7. Example of visualization and reasoning
Mathematical objects and meaning/interpretation
Geometric registers: symbolic, figural
⊥;∥ perpendicular; parallel
∞ infinity
8 number
∀ for all/for every
A point/letter
∃ there exists
E point/letter

8. Duval’s cognitive model of geometrical reasoning:
the role of a figure
• a figure gives us a figural representation of a
geometrical situation which is shorter and easier to be
understood than a representation with linguist speech.
• cognitive apprehensions of figures:
Seeing, constructing and describing a geometrical
figure and its properties
1. Perceptual apprehension
2. Sequential apprehension
3. Discursive apprehension
4. Operative apprehension

9. • It is about physical recognition (shape,
representation, size, brightness, etc.) of a
perceived figure. We should also discriminate
and recognize sub-figures within the perceived
figures since a relevant discrimination or
recognition of these sub-figure units may help
and give cues for problem solving in
geometrical situations.
perceptual apprehension

10. sequential apprehension
• It is about construction of a figure or
description of its construction. Such
construction depends on technical constraints
and also mathematical properties since
construction of a figure may merge different
figural units. It is believed that construction
can help recognition of relationships between
mathematical properties and technical
constraints.

11. discursive apprehension:
• It is about (a) the ability to connect
configuration(s) with geometric principles, (b)
the ability to provide good description,
explanation, argumentation, deduction, use of
symbols, reasoning depending on statements
made on perceptual apprehension, and (c) the
ability to describe figures through geometric
language/narrative texts

12. operative apprehension:
• It is about making modification of a given figure
in various ways to investigate others
configurations:
• the mereological way: dividing the whole given
figure into parts of various shapes and combine
these parts in another figure or sub-figures;
• the optic way: varying the size of the figures; you
can make a shape larger or narrower, or slant, the
shapes can appear differently
• the place way: varying the position or its
orientation.

13. Task
Study your question and showcase your
understanding of
• The critical components of the question
• The actions required to complete the question
basing on Duval’s cognitive model of
geometrical reasoning