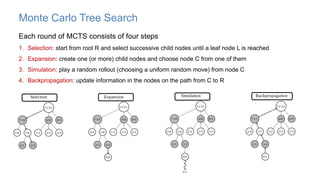
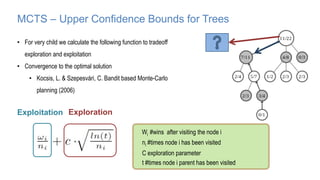
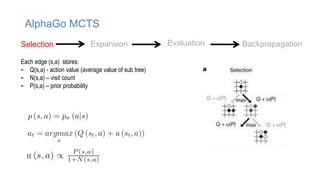
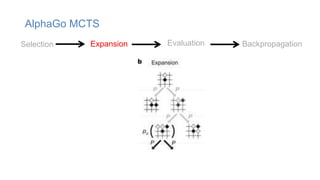
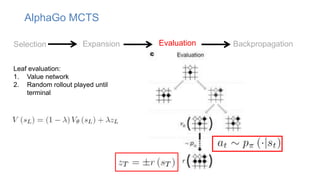
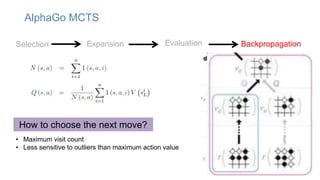
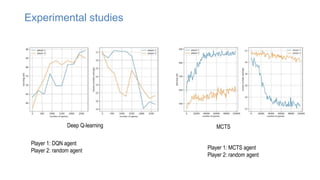
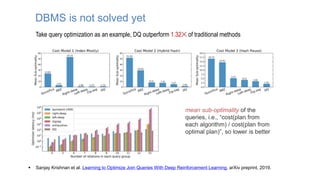
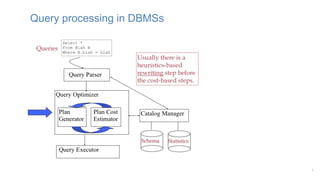
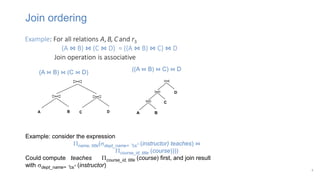
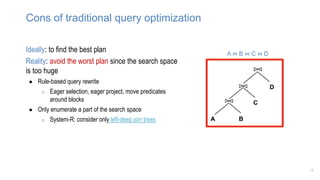
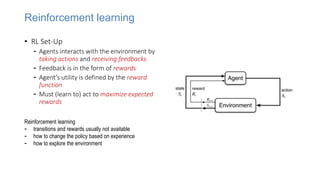
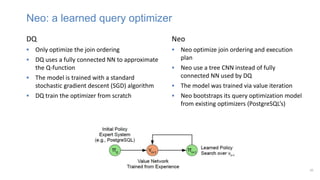
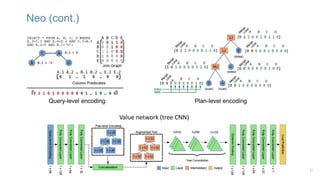
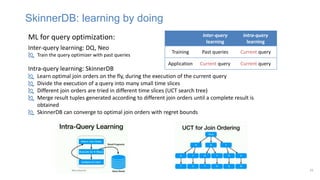
The document discusses using machine learning techniques like reinforcement learning and generative adversarial networks to improve query optimization in databases. Specifically, it summarizes work using deep Q-learning (DQ) and a neural optimizer (Neo) to learn join ordering, as well as using intra-query learning with SkinnerDB. It proposes using generative adversarial networks and Monte Carlo tree search to address shortcomings in existing approaches like lack of training data and balancing exploration vs exploitation. Generative adversarial networks could generate additional training data while Monte Carlo tree search would help optimize join ordering on a per-query basis.

1. Learning to optimize query processing
Learning to Optimize Query
Processing
Qingsong Guo, UDBMS Group, 2020.07.12

2. OUTLINE
1. Is database a solved problem?
2. Introduction to query optimization
3. Query optimization with RL
4. Train the optimizer with GANs

3. 1. Guy Lohman. Is query optimization a “solved” problem. ACM Blog, 2014.
2. Jens Dittrich. Deep Learning (m)eats Databases. VLDB 2017 Keynote.
01 Is database a solved problem?

4. • > 40 years of DB research
• We developed
– fantastic algorithms
– great systems
– clever query processing and storage strategies
– a lot of brilliant stuff
• DBMSs have become fast
– when you look at TPC-C: we are currently able to execute ~half a million transactions per second
– to simple index-lookups, e.g., in a hash table, we are currently at 20 million operations per second
DBMS is a solved problem

5. Take query optimization as an example, DQ outperform 1.32✕ of traditional methods
DBMS is not solved yet
mean sub-optimality of the
queries, i.e., “cost(plan from
each algorithm) / cost(plan from
optimal plan)”, so lower is better
 Sanjay Krishnan et al. Learning to Optimize Join Queries With Deep Reinforcement Learning. arXiv preprint, 2019.

6. 02 Introduction to query optimization
1. Chaudhuri, Surajit. 1998. An overview of query optimization in relational systems. PODS’
98. ACM, NY, USA, 34-43.
2. Yannis E. Ioannidis. 1996. Query optimization. ACM Computing Survey. ACM, NY, USA,
121–123.
3. Ron Avnur and Joseph M. Hellerstein. 2000. Eddies: continuously adaptive query
processing. SIGMOD '00. ACM, New York, NY, USA, 261-272.
4. Viktor Leis, Andrey Gubichev, Atanas Mirchev, Peter Boncz, Alfons Kemper, and
Thomas Neumann. 2015. How good are query optimizers, really?. Proc. VLDB Endow.
9, 3 (November 2015), 204-215.

7. Query processing in DBMSs
7

8. Join ordering
8
Example: For all relations A, B, C and r3
(A ⋈ B) ⋈ (C ⋈ D) = ((A ⋈ B) ⋈ C) ⋈ D
Join operation is associative
(A ⋈ B) ⋈ (C ⋈ D)
((A ⋈ B) ⋈ C) ⋈ D
Example: consider the expression
name, title(dept_name= “cs” (instructor) teaches) ⋈
course_id, title (course))))
Could compute teaches course_id, title (course) first, and join result
with dept_name= “cs” (instructor)

9. Query optimization
● Search space for a given query
○ Query rewrite that transform from one query to another with relational
algebra equivalence
■ σc1∧…∧cn(R) ≡ σc1(…(σcn(R))…) ≡ σcn(…(σc1(R))…)
○ Join order enumeration
■ R ⋈ (S ⋈ T) ≡ (R ⋈ S) ⋈ T
● Cost estimation
○ Assign a cost to each plan in the search space with the statistics on the
database
● Enumeration algorithm
○ Search the best execution plan from the space
9

10. Search space for join-ordering
• Consider finding the best join-order for r1 ⋈ r2 ⋈ . .
. ⋈ rn.
• There are (2(n – 1))!/(n – 1)! different join orders for
above expression. With n = 7, the number is
665280, with n = 10, the number is greater than 176
billion!
• No need to generate all the join orders. Using
dynamic programming, the least-cost join order for
any subset of {r1, r2, . . . rn} is computed only once
and stored for future use.
Join tree structure number
Left-deep tree n!
Right-deep tree n!
Zig-zag n!2n-2
Bushy (2n-2)!/(n-1)!

11. Left-deep join with DP
Left-deep join order tree
 Dynamic programming
11
SELECT SUM(S.salary * T.rate)
FROM Employees as E, Salaries as S,
Taxes as T
WHERE E.position = S.position AND
T.country = S.country AND
E.position = ‘Manager 1’
If join {E,S}, it looks up the the relevant, previously
computed results as follows:
 Best({E, S}) = Best({E}) + Best({S}) + J({E}, S)
Remaining
Relations
Joined
Relations
Best
{E, S} {T} J(T), i.e., scan cost of T
{E, T} {S} J(S)
{T, S} {E} J(E)
Remaining
Relations
Joined
Relations
Best
{ } {E, S, T}
min {Best({E,T})+J(S)+J({E,T}, S),
Best({E,S}) + J(T) + J({E,S}, T),
Best({T,S}) + J(E) + J({T,S}, E) }
Remaining
Relations
Joined
Relations
Best
{T} {E, S} Best({E}) + Best({S}) + J({E}, S)

12. Cons of traditional query optimization
12
Ideally: to find the best plan
Reality: avoid the worst plan since the search space
is too huge
● Rule-based query rewrite
○ Eager selection, eager project, move predicates
around blocks
● Only enumerate a part of the search space
○ System-R: consider only left-deep join trees
A ⋈ B ⋈ C ⋈ D

13. Cost of optimization
• With dynamic programming time complexity of optimization with bushy trees is O(3n).
– With n = 10, this number is 59000 instead of 176 billion!
• Space complexity is O(2n)
• To find best left-deep join tree for a set of n relations:
– Consider n alternatives with one relation as right-hand side input and the other relations as left-hand
side input.
– Modify optimization algorithm:
• Replace “for each non-empty subset S1 of S such that S1  S”
• By: for each relation r in S
let S1 = S – r .
• If only left-deep trees are considered, time complexity of finding best join order is O(n 2n)
– Space complexity remains at O(2n)
• Cost-based optimization is expensive, but worthwhile for queries on large datasets (typical
queries have small n, generally < 10)

14. 1. DQ: S. Krishnan, Z. Yang, K. Goldberg, J. Hellerstein, and I. Stoica. Learning to Optimize Join
Queries With Deep Reinforcement Learning. arXiv:1808.03196v2, Jan 2019.
2. Neo: Ryan Marcus, Parimarjan Negi, Hongzi Mao, Chi Zhang, Mohammad Alizadeh, Tim
Kraska, Olga Papaemmanouil, Nesime Tatbul. Neo: A Learned Query Optimizer. PVLDB, 12(11):
1705-1718, 2019.
3. SkinnerDB: I. Trummer, S. Moseley, D. Maram, S. Jo, and J. Antonakakis. SkinnerDB: Regret-
bounded Query Evaluation via Reinforcement Learning. PVLDB, 11(12):2074–2077, 2018.
4. Xiang Yu, Guoliang Li, Chengliang Chai, Nan Tang. Reinforcement Learning with Tree-LSTM for
Join Order Selection. ICDE 2020.
03 Query optimization with RL

15. Automatic query optimization
● Traditional query optimization
- Relational algebraic equivalence
- Join order enumeration
● Adaptive query processing
- Traditional optimize-then-execute paradigm
- Data is changing over time
● Learning to optimize with deep reinforcement learning
- DQ (Deep Q-learning)
- Neo (Neural Optimizer)
- SkinnerDB
15

16. Reinforcement learning
• RL Set-Up
- Agents interacts with the environment by
taking actions and receiving feedbacks
- Feedback is in the form of rewards
- Agent’s utility is defined by the reward
function
- Must (learn to) act to maximize expected
rewards
Reinforcement learning
- transitions and rewards usually not available
- how to change the policy based on experience
- how to explore the environment

17. Markov Decision Process (MDP)
• Set of states S, set of actions A, initial state S0
• Transition model P(s,a,s’)
- P( [1,1], up, [1,2] ) = 0.8
• Reward function r(s)
- r( [4,3] ) = +1
• Goal: maximize cumulative reward in the long
run
• Policy: mapping from S to A
- (s) or (s,a) (deterministic vs. stochastic)
+1
-1
START
actions: UP, DOWN, LEFT, RIGHT
80% move UP
10% move LEFT
10% move RIGHT
1 2 3 4
1
2
3
• reward +1 at [4,3], -1 at [4,2]
• reward -0.04 for each step
• what’s the strategy to achieve max reward?
MDP solvers
- Dynamic programming
- Monte Carlo methods
- Deep Q-lerning

18. DQ: optimize join with deep Q-learning
RL can be modeled as a Markov Decision Process (MDP)
Formulate join ordering as an MDP (G, c, G’, J)
● States G: the remaining relations to be joined.
● Actions c: a valid join out of the remaining relations.
● Next states G’: naturally, this is the old “remaining
relations” set with two relations removed and their
resultant join added.
● Reward J: estimated cost of the new join.
Apply Q-learning to solve the join-ordering MDP
● Q-function: Q(G, c) = J(c) + minc’ Q(G’, c’)
● describes the long-term cost of each join: the
cumulative cost if we act optimally for all
subsequent joins after the current join decision.
18
Learning algorithm:
(1)Start with the initial query graph,
(2)Find the join with the lowest Q(G, c),
(3)Update the query graph and repeat.

19. 19
To learn the Q-function (Training the model)
1. Training data: To learn the Q-function we first need to observe past execution data. DQ can
accept a list of (G, c, G’, J) from any underlying optimizer (run a classical left-deep dynamic
program).
 For example: (G, c, G’, J) = ({E, S, T}, join(S, T), {E, ST}, 110) means that we start with the initial query graph
(state) and joining S and T together (action).
2. Featurization of states and actions
 Feed states G and actions c into the network as fixed-length feature vectors
 1-hot vectors to encode: (1) the set of all attributes AG present in the query graph, out of all attributes in
the schema, (2) the participating attributes AL from left side of the join, and (3) those AR from right side of
the join
Training the optimizer in DQ

20. 20
DQ
 Only optimize the join ordering
 DQ uses a fully connected NN to approximate
the Q-function
 The model is trained with a standard
stochastic gradient descent (SGD) algorithm
 DQ train the optimizer from scratch
Neo: a learned query optimizer
Neo
 Neo optimize join ordering and execution
plan
 Neo use a tree CNN instead of fully
connected NN used by DQ
 The model was trained via value iteration
 Neo bootstraps its query optimization model
from existing optimizers (PostgreSQL’s)

21. 21
Neo (cont.)
Plan-level encoding
Query-level encoding
Value network (tree CNN)

22. 22
ML for query optimization:
Inter-query learning: DQ, Neo
 Train the query optimizer with past queries
Intra-query learning: SkinnerDB
 Learn optimal join orders on the fly, during the execution of the current query
 Divide the execution of a query into many small time slices
 Different join orders are tried in different time slices (UCT search tree)
 Merge result tuples generated according to different join orders until a complete result is
obtained
 SkinnerDB can converge to optimal join orders with regret bounds
SkinnerDB: learning by doing
Inter-query
learning
Intra-query
learning
Training Past queries Current query
Application Current query Current query

23. 1. Generative adversarial networks
2. Monte Carlo tree search.
3. AlphaGo : D. Silver, et al. Mastering the game of go with deep neural networks and tree
search. In Nature. Nature Research, 2016.
04 Adversarial training for query optimizer

24. Shortcomings of the existing methods
• Shortcoming 1: lack of training data
– DQ learns from scratch and takes very long time for training
– Neo relies on the exiting knowledge but with limited improvement
– SkinnerDB tries to learn an adaptive execution by dividing the data into many small
execution plan
• Shortcoming 2: Lack of capability to tradeoff exploitation and exploration
– DQ relies on deep Q-learning tries to exhaust all enumerations which is
– Neo relies on value iteration which takes a long time to converge
• Our solution
– Generative adversarial neural network (GAN) for the shortcoming 1
– Monte Carlo search tree (MCTS) to address the shortcoming 2

25. Generative adversarial network (GAN)
MinMax Game (Zero-sum gaming)
• Generator tries to fool discriminator (i.e. generate realistic samples)
• Discriminator tries to distinguish fake from real samples
• Each tries to minimize the objective function maximized by the other
Training set
𝑥1, ⋯ , 𝑥𝑛 ~𝑝𝑑𝑎𝑡𝑎
Discriminator 𝐷
(Binary classifier)
Generator 𝐺
min
𝐺
max
𝐷
𝑉 𝐷, 𝐺 = 𝔼𝑥~𝑝𝑑𝑎𝑡𝑎(𝑥)[log 𝐷 𝑥 ] + 𝔼𝑧~𝑝𝑧(𝑧)[log(1 − 𝐷(𝐺 𝑧 ))]
[Goodfellow et al., 2014]
1/0
𝐺𝑧
𝑥
noise 𝑧

26. Query optimization via adversarial training
MinMax Game
• The discriminator D a cascaded joins of value network connecting all tables together
• The generator G is a cascaded series of the MCTS improved policy (i.e. generate realistic
samples)
• Each tries to minimize the objective function maximized by the other
Training set:
𝑒𝑥𝑒𝑐𝑢𝑡𝑖𝑜𝑛 𝑝𝑙𝑎𝑛𝑠: 𝑥1, ⋯ , 𝑥𝑛
Discriminator 𝐷
(Binary classifier)
Generator 𝐺
min
𝐺
max
𝐷
(𝐷, 𝐺) = 𝔼𝑥[log 𝐷 𝑥 ] + 𝔼𝑧[log(1 − 𝐷(𝐺 𝑧 ))]
1/0
𝐺𝑧
𝑥
Random plan 𝑧

27. Monte Carlo Tree Search (MCTS)
• Monte Carlo Experiments : repeated random sampling to obtain
numerical results
• Search method
• Method for making optimal decisions in artificial
intelligence (AI) problems
• The strongest Go AIs (Fuego, Pachi, Zen, and Crazy
Stone) all rely on MCTS

28. Monte Carlo Tree Search
Each round of MCTS consists of four steps
1. Selection: start from root R and select successive child nodes until a leaf node L is reached
2. Expansion: create one (or more) child nodes and choose node C from one of them
3. Simulation: play a random rollout (choosing a uniform random move) from node C
4. Backpropagation: update information in the nodes on the path from C to R

29. MCTS – Upper Confidence Bounds for Trees
• For very child we calculate the following function to tradeoff
exploration and exploitation
• Convergence to the optimal solution
• Kocsis, L. & Szepesvári, C. Bandit based Monte-Carlo
planning (2006)
Exploration
Exploitation
Wi #wins after visiting the node i
ni #times node i has been visited
C exploration parameter
t #times node i parent has been visited

30. AlphaGo MCTS
Selection Expansion Evaluation Backpropagation
Each edge (s,a) stores:
- Q(s,a) - action value (average value of sub tree)
- N(s,a) – visit count
- P(s,a) – prior probability

31. AlphaGo MCTS
Selection Expansion Evaluation Backpropagation

32. AlphaGo MCTS
Selection Expansion Evaluation Backpropagation
Leaf evaluation:
1. Value network
2. Random rollout played until
terminal

33. AlphaGo MCTS
Selection Expansion Evaluation Backpropagation
How to choose the next move?
• Maximum visit count
• Less sensitive to outliers than maximum action value

34. Experimental studies
Learning process of Deep Q-Learning:
1. Offline learning with planning, where batches of
state-action pairs were stored and the network was
trained on these batches
2. The playing policy was an 𝜺-greedy policy which
means that an exploration factor 𝜺 was chosen
3. Take ReLu function as an activation function
4. The agent played 300 episodes against random
player and measured the winning rate
Learning process of MCTS:
1. The agent takes 1M episodes, but the learning is a lot faster (a
few hours)
2. To store a tree of 1M episodes it takes around 800MB and it is
growing when the agent continues learning. So it is a lot more
than the CNN which stayed constant through all the learning
process.
3. The graph below shows the winning rate of the MCTS agent
against random player as the learning progresses.
A tik-tac-toe game with 10 columns and 10 rows
 The training stops when agent win over 80%

35. Experimental studies
Deep Q-learning MCTS
Player 1: DQN agent
Player 2: random agent Player 1: MCTS agent
Player 2: random agent

36. THANKS
Does anyone have any questions?

37. Reference
• Noseong Park et al.. Data Synthesis based on Generative Adversarial Networks. PVLDB, 11 (10): 1071-1083, 2018.
• Tim Kraska et al.. The Case for Learned Index Structures. InSIGMOD’18, June 10–15, 2018.
• Guy Lohman. Is query optimization a “solved” problem. ACM Blog, 2014.
• Jens Dittrich. Deep Learning (m)eats Databases. VLDB 2017 Keynote.
• Alec Radford et al.. Unsupervised representation learning with Deep convolutional generative adversarial networks.
ICLR 2016.
• Sanjay Krishnan et al.. Learning to Optimize Join Queries With Deep Reinforcement Learning. arXiv preprint, 2019.
• Tim Kraska et al.. SageDB: A Learned Database System. CIDR 2019.
• Viktor Leis et al.. How good are query optimizers, really? PVLDB 2015.
• Wei Wang et al.. Database Meets Deep Learning: Challenges and Opportunities. SIGMOD Record 2016.
• Ian J. Goodfellow et al. Generative Adversarial Nets. NIPS 2014.
• Kai Arulkumaran et al. A Brief Survey of Deep Reinforcement Learning. IEEE Signal Processing Magazine 2017.
• Manasi Vartak. MODELDB: Opportunities and Challenges in Managing MachineLearning Models. CIDR 2017.
• Mu Li et al.. Scaling Distributed Machine Learning with the Parameter Server. OSDI 2014.
• Prediction Serving. https://ucbrise.github.io/cs294-rise-fa16/prediction_serving.html
• Daniel Crankshaw et al.. Clipper: A Low-Latency Online Prediction Serving System. NSDI 2017.
• DQN source code: sites.google.com/a/ deepmind.com/dqn/