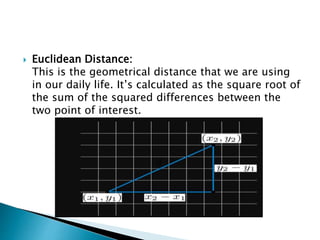
The document discusses machine learning algorithms with a focus on k-nearest neighbors (KNN), a non-parametric and lazy supervised algorithm that classifies data points based on the majority voting from their nearest neighbors. It explains the principles of KNN, how to determine the value of k, the importance of distance metrics, and the algorithm's applications in various fields such as banking and politics. KNN is noted for its high accuracy for small datasets but has challenges related to computational expense and sensitivity to data scale.

3.  Most of the machine learning
algorithms are parametric. What do we mean by
parametric? Let’s say if we are trying to model an linear
regression model with one dependent variable and one
independent variable. The best fit we are looking is the
line equations with optimized parameters.
 The parameters could be the intercept and coefficient. For
any classification algorithm, we will try to get a boundary.
Which successfully separates different target classes.
 Let’s say for support vector machine we will try to find
the margins and the support vectors. In this case, also we
will have some set of parameters. Which needs to be
optimized to get decent accuracy.

4.  But today we are going to learn a different
kind of algorithm which is non-
parametric classification algorithm.
 Let’s walk through to get know how we can
do that. Just to give you one line summary.
“The algorithm uses the neighbour points
information to predict the target class”.

5. KNN is a supervised algorithm (which means
that the training data is labeled, it is non-
parametric and lazy (instance based).
 The simple version of the K-nearest
neighbour classifier algorithms is to predict
the target label by finding the nearest
neighbour class. The closest class will be
identified using the distance measures like
Euclidean distance.

6.  We often judge people by their vicinity to the
group of people they live with. People who
belong to a particular group are usually
considered similar based on the
characteristics they possess. This is the
simple principle on which the KNN algorithm
works – “Birds of the same feather flock
together.”

7. Let us consider the simple example of Game of Thrones to
understand the KNN algorithm.
Imagine you have to design a classification algorithm to identify
whether a stranger is a Westerosi or a Dothraki. There are
different features that can be used to classify which group the
stranger belongs to. For instance, if the person is a Dothraki he
is likely to have greater muscle mass whereas if he is a
Westerosi, he is likely to be wealthy. In this case, wealth and
muscle mass are the independent variables and features. When
you place the stranger among the bulk of Westerosi and Dothraki
clan, you can classify the person as a Dothraki or Westerosi
based on majority voting i.e. based on whether the maximum
number of nearest neighbors belong to Westerosi clan or the
Dothraki clan.

8.  Let m be the number of training data samples. Let p
be an unknown point.
 Store the training samples in an array of data points
arr[]. This means each element of this array
represents a tuple (x, y).
 for i=0 to m: Calculate Euclidean distance d(arr[i], p).
 Make set S of K smallest distances obtained. Each of
these distances correspond to an already classified
data point.
 Return the majority label among S.

9.  Let m be the number of training data
samples. Let p be an unknown point.
 Store the training samples in an array of data
points arr[]. This means each element of this
array represents a tuple (x, y).
 for i=0 to m: Calculate Euclidean distance
d(arr[i], p).
 Make set S of K smallest distances obtained.
Each of these distances corresponds to an
already classified data point.
 Return the majority label among S.

12.  Because it does not explicitly learns the model, but
it saves all the training data and uses the whole
training set for classification or prediction. This is in
contrast to other techniques like SVM, where you can
discard all non support vectors without any problem.
 This means that the training process is very fast, it
just saves all the values from the data set. The real
problem is the huge memory consumption (because
we have to store all the data) and time complexity at
testing time (since classifying a given observation
requires a run down of the whole data set) . But in
general it’s a very useful algorithm in case of small
data sets (or if you have lots of time and memory) or
for educational purposes.

13.  The KNN classification consist of some cases
which are k=1 and k=K.where k=K it is quite
obvious that the accuracy *might* increase when
you increase k but the computation cost also
increases.
 An interesting idea is to find the distance metrics
using machine learning (mainly by converting the
data to vector space, represent the differences
between objects as distances between vectors
and learn those differences, but this is another
topic, we will talk about this later).

14.  1. Standardization
When independent variables in training data are measured
in different units, it is important to standardize variables
before calculating distance. For example, if one variable is
based on height in cms, and the other is based on weight
in kgs then height will influence more on the distance
calculation. In order to make them comparable we need to
standardize.
 2. Outlier
Low k-value is sensitive to outliers and a higher K-value is
more resilient to outliers as it considers more voters to
decide prediction.

15.  At this point, you’re probably wondering how to pick the variable
K and what its effects are on your classifier. Well, like most
machine learning algorithms, the K in KNN is a hyperparameter
that you, as a designer, must pick in order to get the best
possible fit for the data set. Intuitively, you can think of K as
controlling the shape of the decision boundary we talked about
earlier.
 When K is small, we are restraining the region of a given
prediction and forcing our classifier to be “more blind” to the
overall distribution. A small value for K provides the most
flexible fit, which will have low bias but high variance.
Graphically, our decision boundary will be more jagged. On the
other hand, a higher K averages more voters in each prediction
and hence is more resilient to outliers. Larger values of K will
have smoother decision boundaries which means lower variance
but increased bias.

17.  Euclidean Distance
 Manhattan Distance
 Chebyshev Distance

18.  Euclidean Distance:
This is the geometrical distance that we are using
in our daily life. It’s calculated as the square root of
the sum of the squared differences between the
two point of interest.

21.  Chebyshev distance is a distance metric
which is the maximum absolute distance in
one dimension of two N dimensional points.
It has real world applications in Chess,
Warehouse logistics and many other fields.
 It is, also, known as Tchebychev distance,
maximum metric, chessboard distance and
L∞ metric.
 Chebyshev distance = MAXIMUM (|xi - yi|)
where i is 1 to N

22.  In chess, all the three distances are used as
follows:
 The distance between squares on the chessboard
for rooks is measured in Manhattan distance
 Kings and queens use Chebyshev distance
 bishops use the Manhattan distance (between
squares of the same color) on the chessboard
rotated 45 degrees, i.e., with its diagonals as
coordinate axes.
 To reach from one square to another, only kings
require the number of moves equal to the distance
(euclidean distance) rooks, queens and bishops
require one or two moves

23.  Let (Xi, Ci) where i = 1, 2……., n be data
points. Xi denotes feature values & Ci denotes
labels for Xi for each i.
Assuming the number of classes as ‘c’
Ci ∈ {1, 2, 3, ……, c} for all values of i
 Let x be a point for which label is not known,
and we would like to find the label class using
k-nearest neighbour algorithms.

25.  It is very simple algorithm to understand and
interpret.
 It is very useful for nonlinear data because
there is no assumption about data in this
algorithm.
 It is a versatile algorithm as we can use it for
classification as well as regression.
 It has relatively high accuracy but there are
much better supervised learning models than
KNN.

26.  It is computationally a bit expensive
algorithm because it stores all the training
data.
 High memory storage required as compared
to other supervised learning algorithms.
 Prediction is slow in case of big N.
 It is very sensitive to the scale of data as well
as irrelevant features.

27. The following are some of the areas in which KNN can be applied
successfully −
 Banking System
KNN can be used in banking system to predict weather an
individual is fit for loan approval? Does that individual have the
characteristics similar to t he defaulters one?
Calculating Credit Ratings
 KNN algorithms can be used to find an individual’s credit rating
by comparing with the persons having similar traits.
Politics
 With the help of KNN algorithms, we can classify a potential voter
into various classes like “Will Vote”, “Will not Vote”, “Will Vote to
Party ‘Congress’, “Will Vote to Party ‘BJP’.