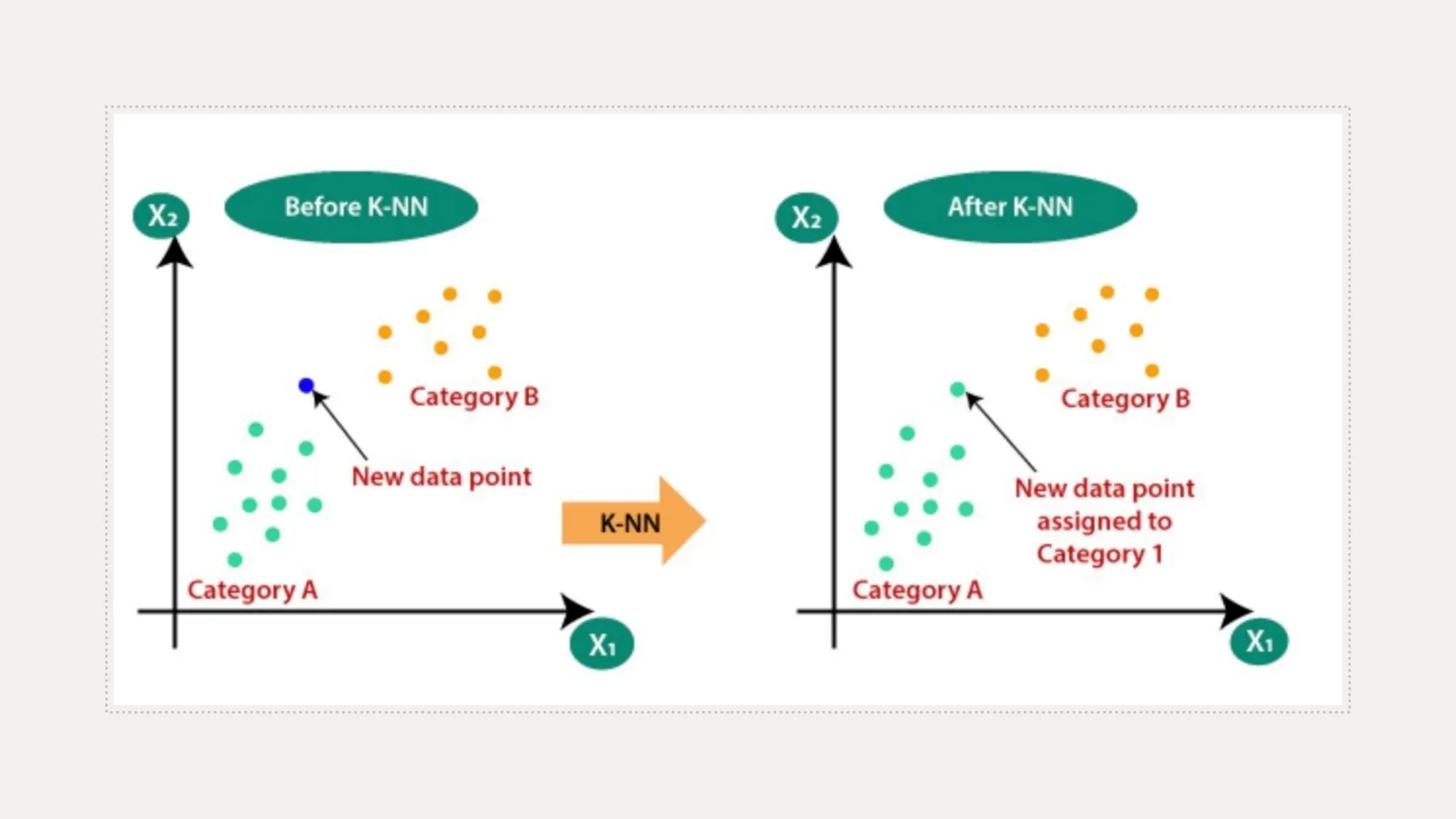
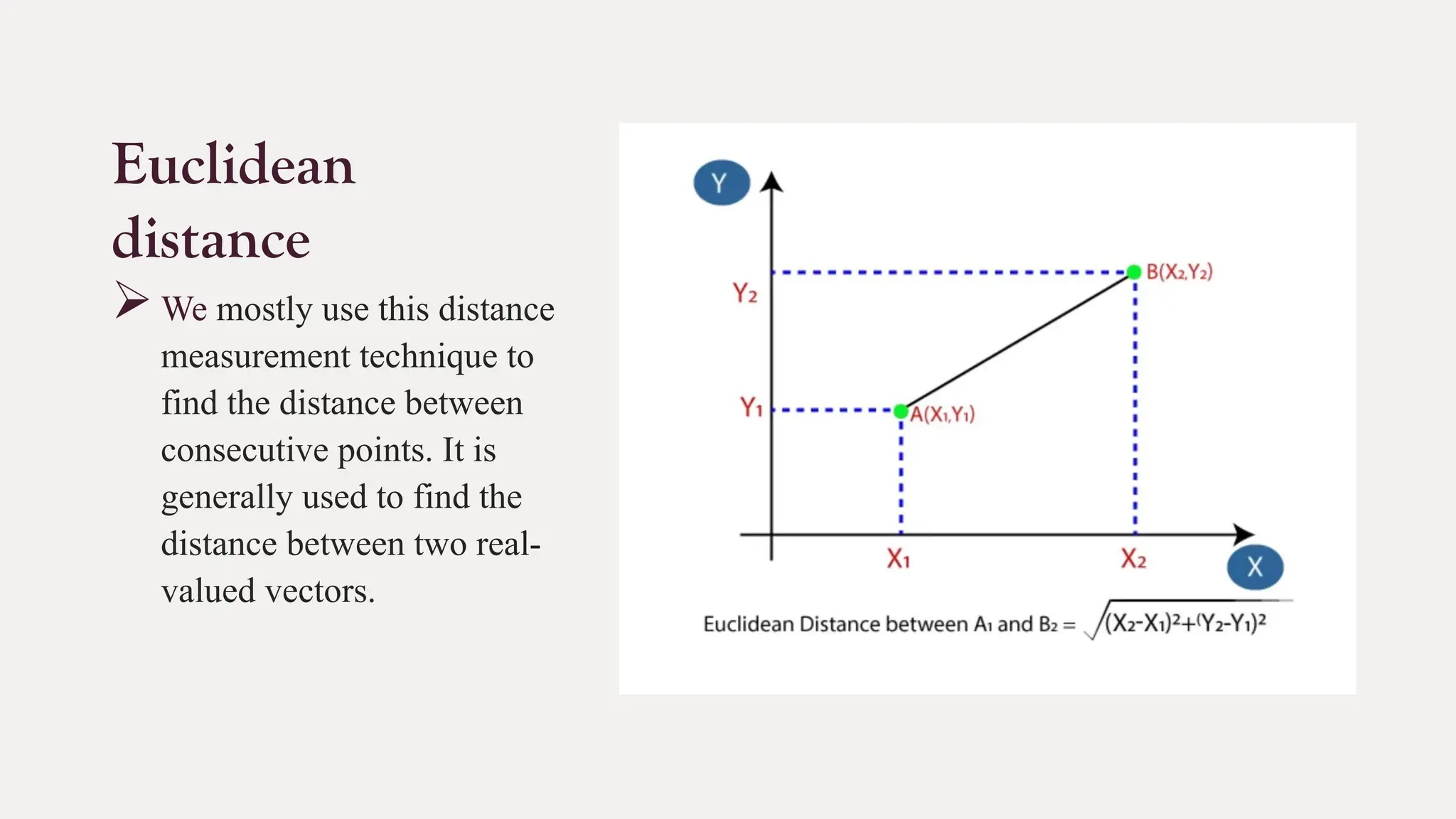
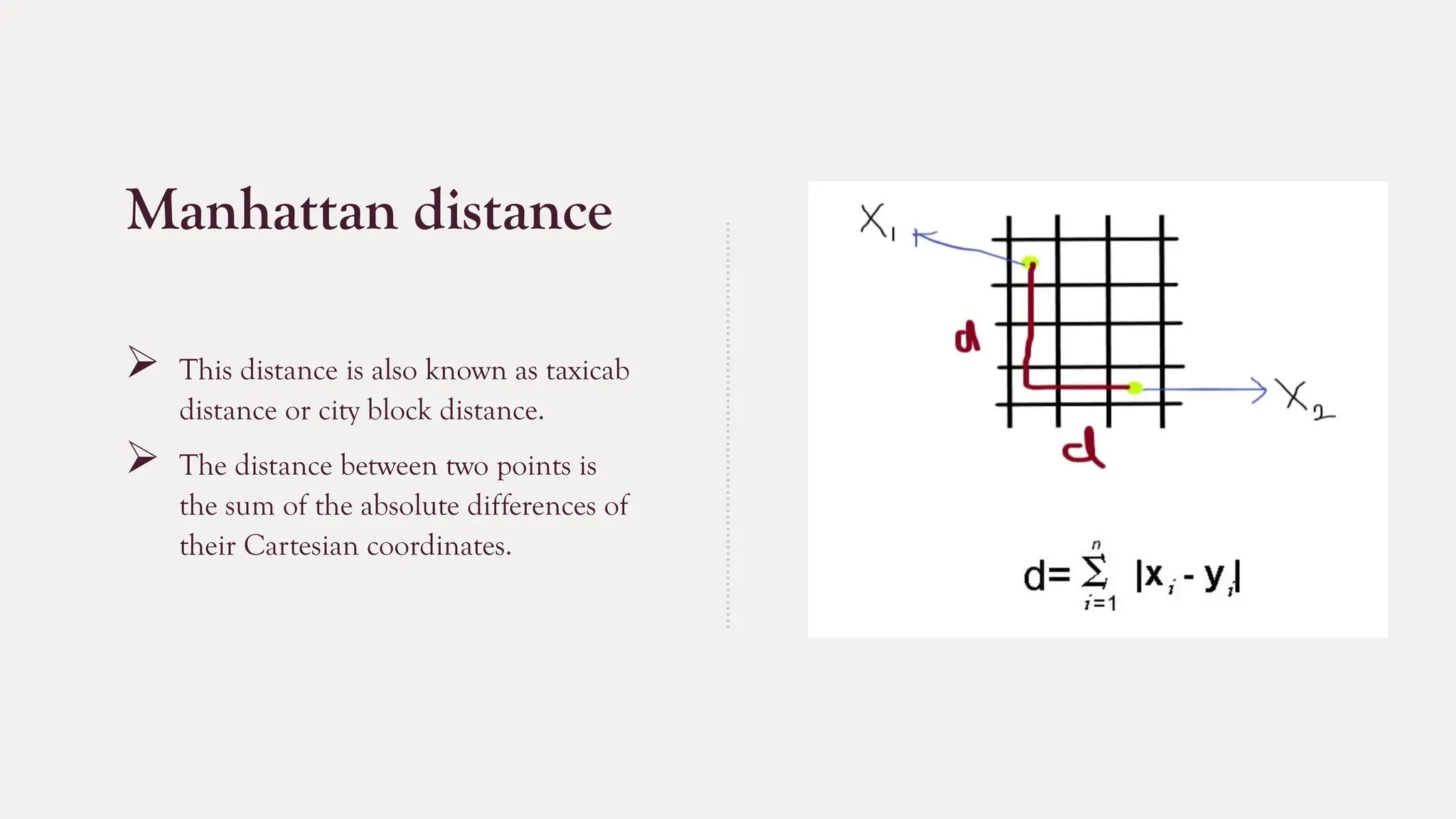
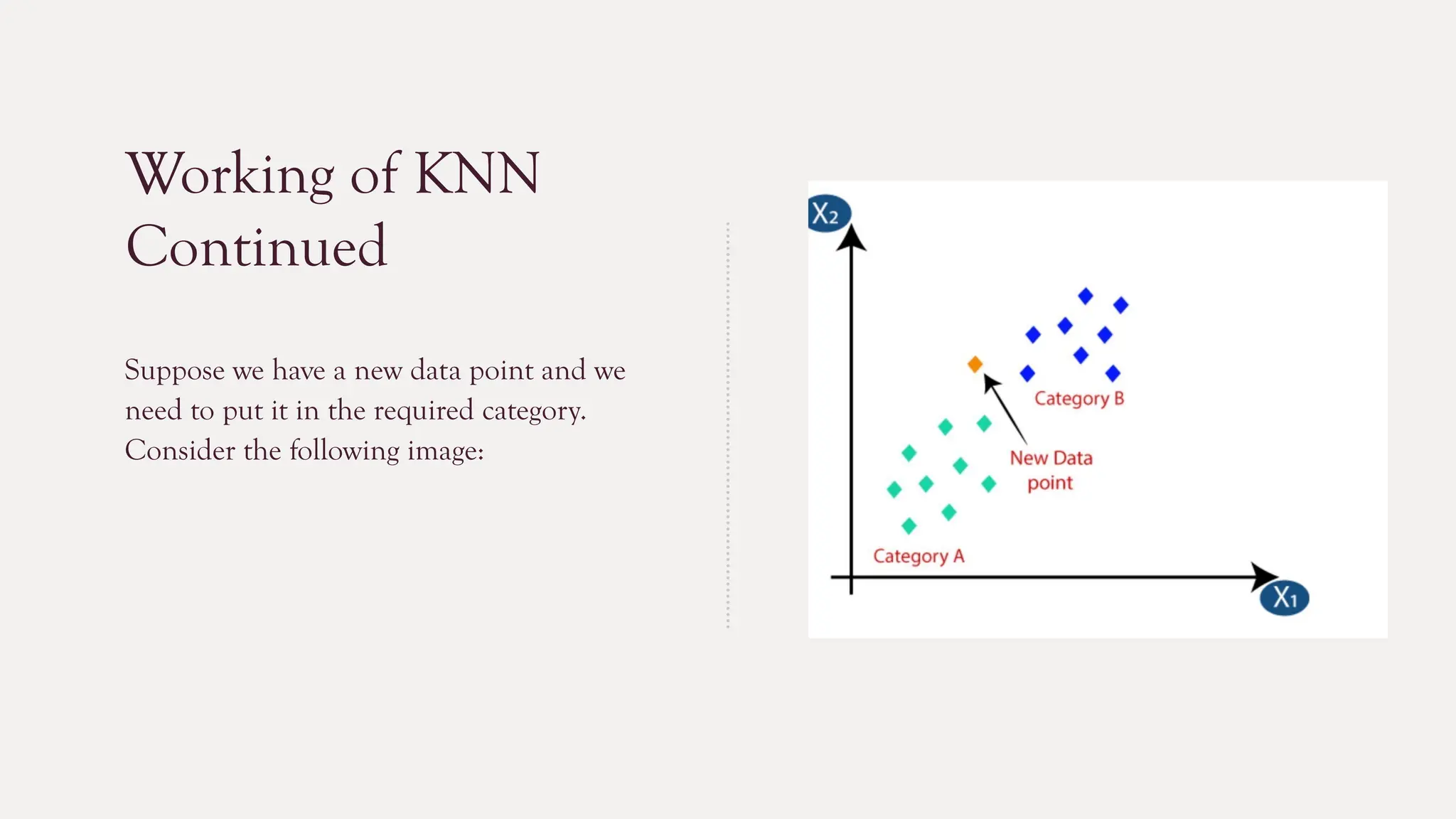
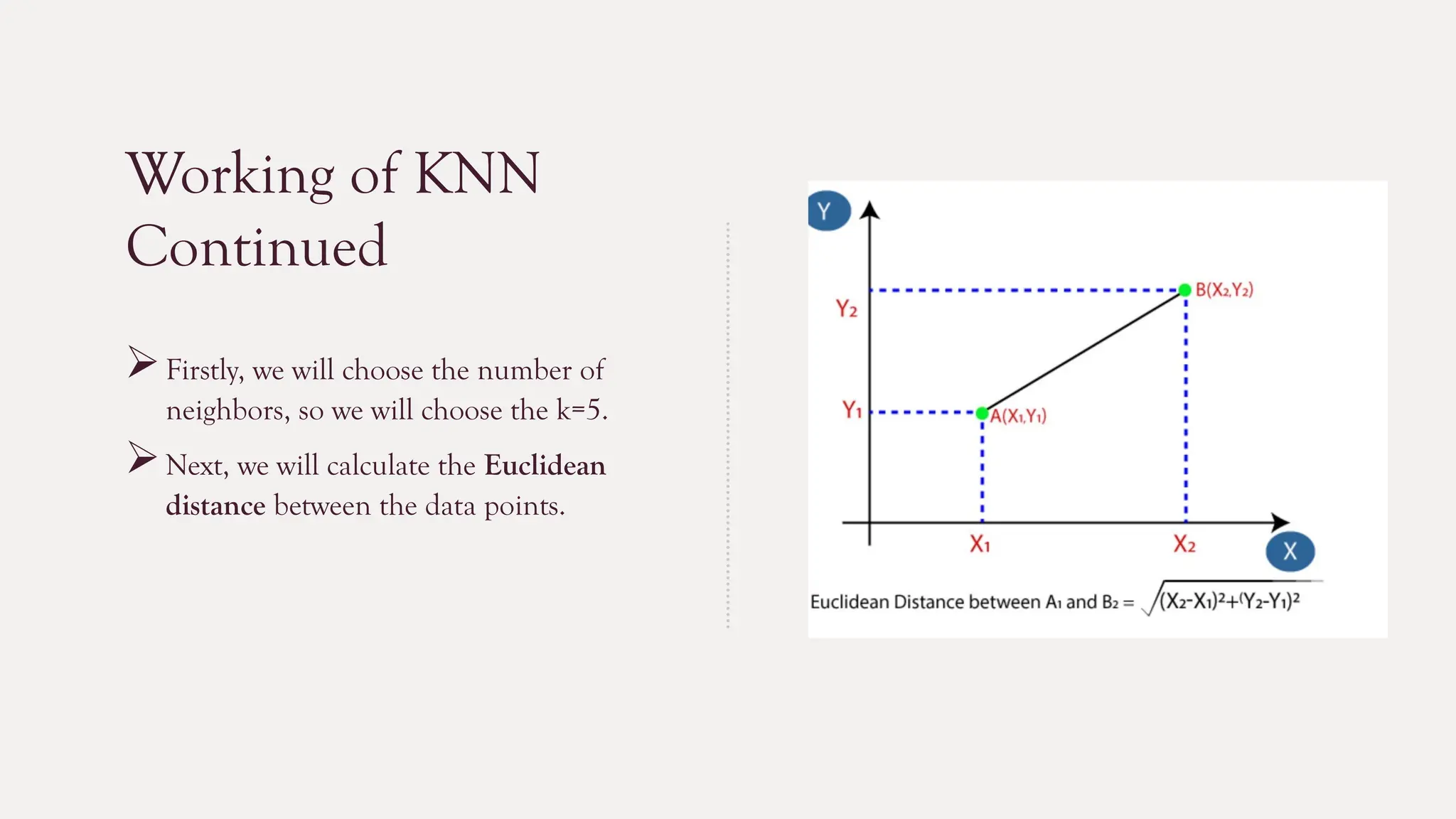
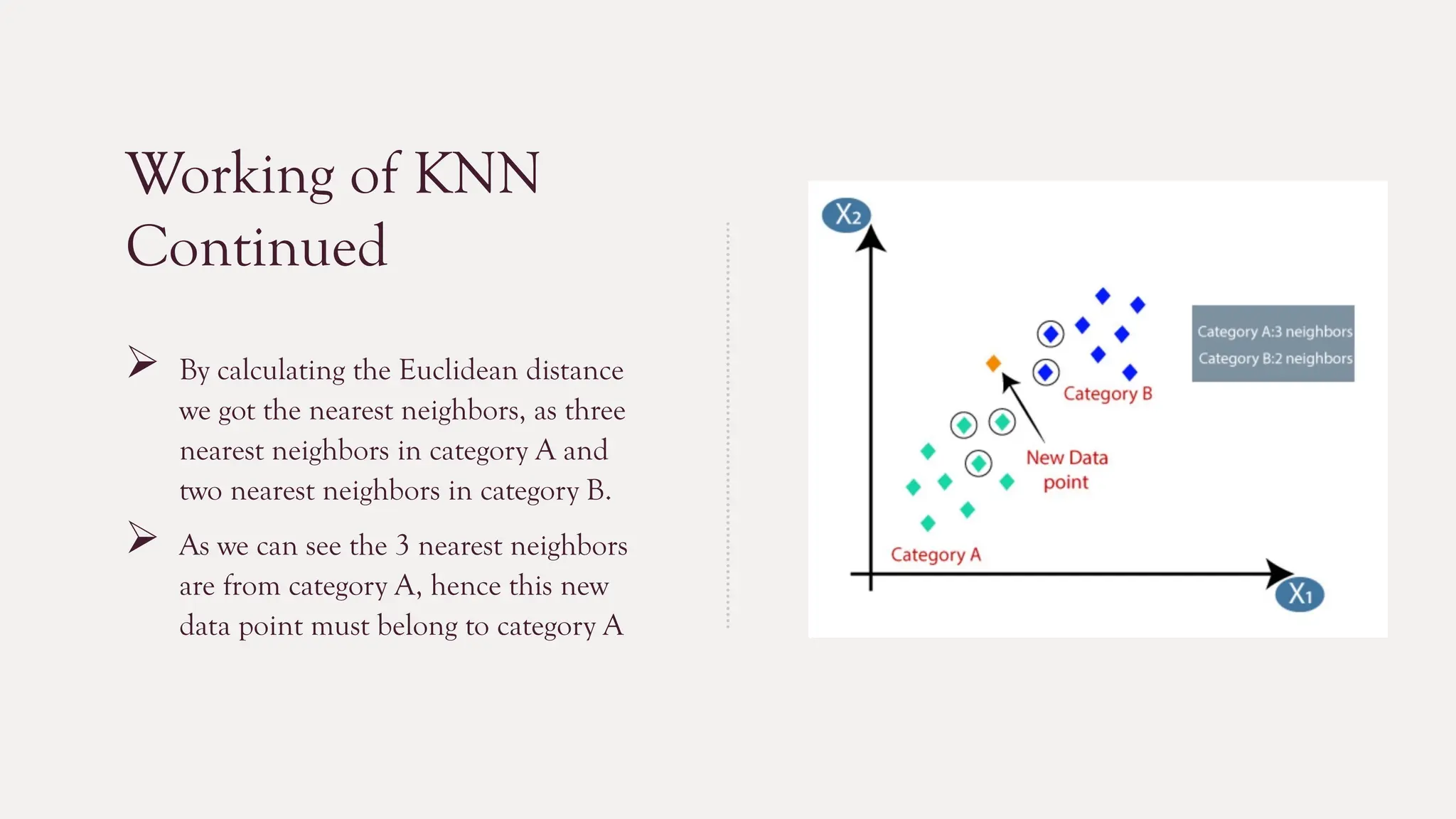
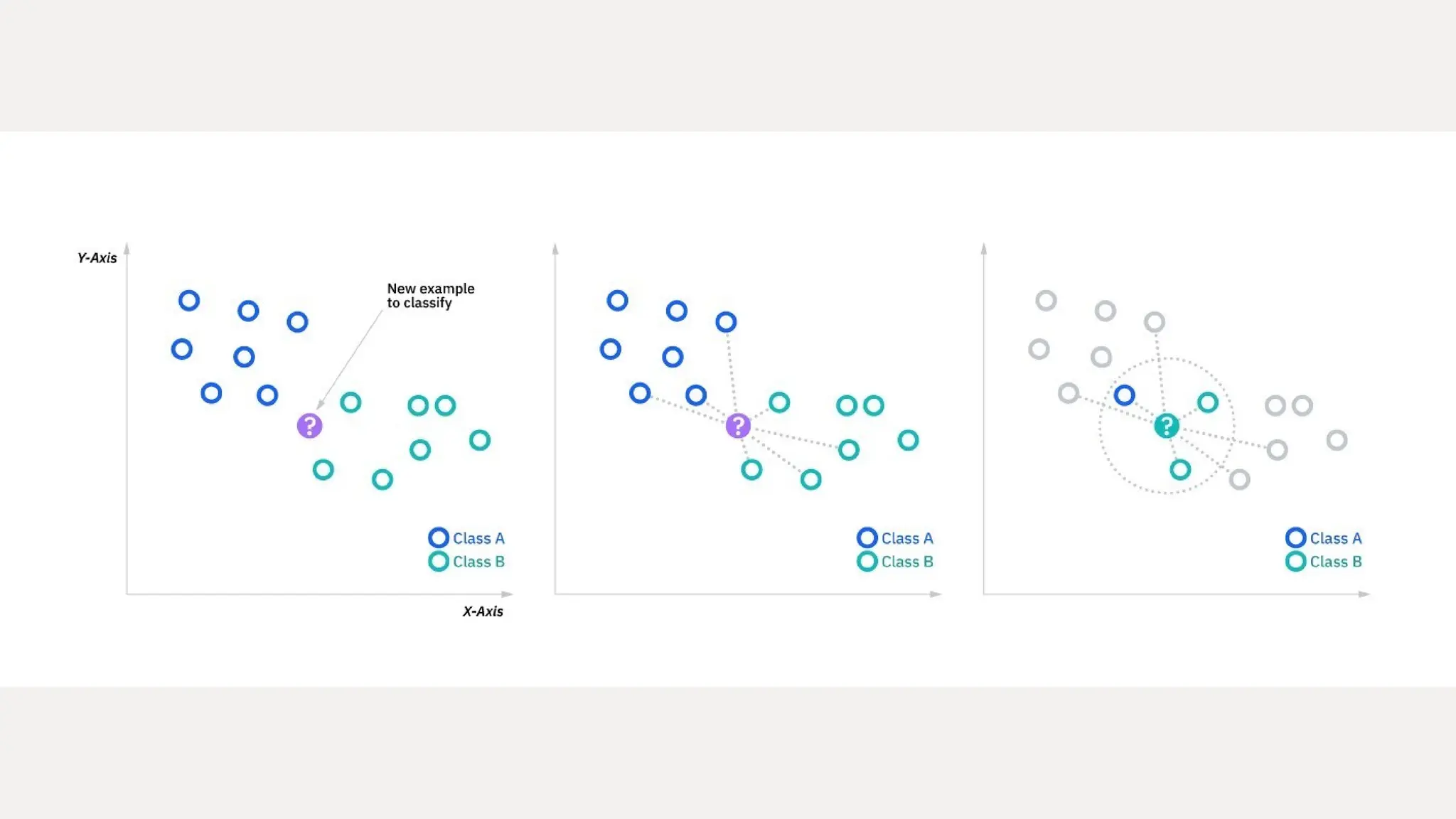
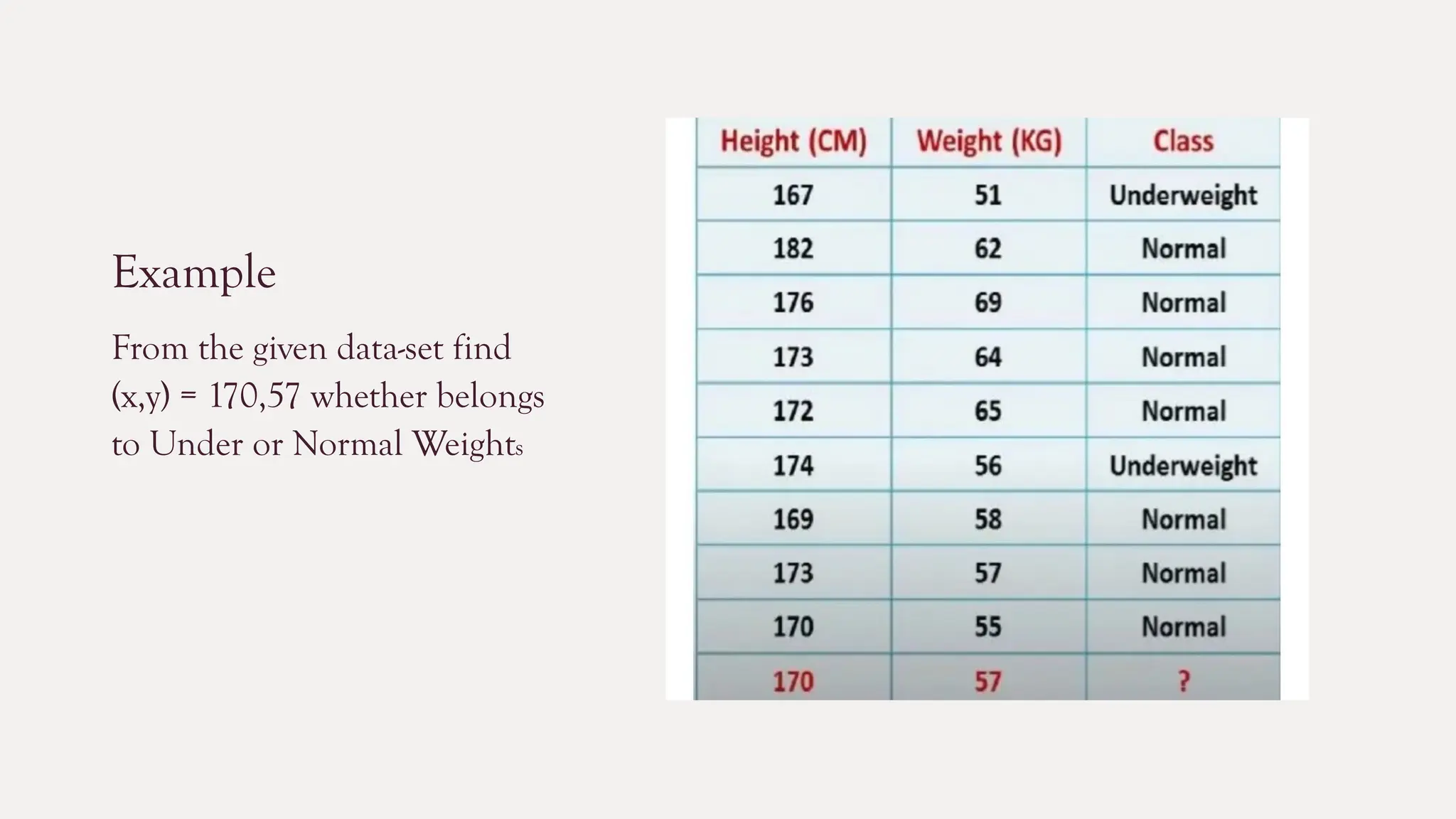
The k-nearest neighbors (k-NN) algorithm is a straightforward machine learning method primarily used for classification tasks, relying on similarity measures to classify data points based on their nearest neighbors. It is a lazy and non-parametric learning algorithm that does not require a training phase but instead uses all training instances during testing, making it efficient for certain tasks but computationally expensive with large datasets. While k-NN has advantages like simplicity and versatility, it also has drawbacks such as high memory requirements and sensitivity to high dimensionality.

1. K-Nearest Neighbors
(KNN)

2. KNN introduction
K-Nearest Neighbour is one of the simplest Machine Learning algorithms based on
Supervised Learning technique.
K-NN algorithm can be used for Regression as well as for Classification but mostly
it is used for the Classification problems.
KNN works on the principal of similarity measure.
In KNN classification, the output is a class membership. The given data point is
classified based on the majority of type of its neighbors.

3. Properties of KNN
Lazy learning algorithm − KNN is a lazy learning algorithm because it does not
require any training data points for model generation. All training data will be used
in the testing phase. This makes training faster and testing slower. So, the testing
phase requires more time and memory resources.
Non-parametric learning algorithm − The KNN algorithm does not make any
assumptions about the underlying data distribution, so it is well-suited for problems
where the boundary is non-linear.

4. Need of KNN
Suppose there are two categories, i.e., Category A and Category B, and we have a
new data point x1, so this data point will lie in which of these categories.
To solve this type of problem, we need a K-NN algorithm. With the help of K-NN,
we can easily identify the category or class of a particular dataset.

6. Distance Measurement
ØEuclidean distance
ØManhattan distance
ØMinkowski distance
ØHamming distance
ØNote: We Mostly use Euclidean Distance in KNN

7. Euclidean
distance
We mostly use this distance
measurement technique to
find the distance between
consecutive points. It is
generally used to find the
distance between two real-
valued vectors.

8. Manhattan distance
 This distance is also known as taxicab
distance or city block distance.
 The distance between two points is
the sum of the absolute differences of
their Cartesian coordinates.

9. Working of KNN
 The K-NN working can be explained on the basis of the below algorithm:
 Step-1: Select the number K of the neighbors
 Step-2: Calculate the Euclidean distance of K number of neighbors
 Step-3: Take the K nearest neighbors as per the calculated Euclidean distance.
 Step-4: Among these k neighbors, count the number of the data points in each category.
 Step-5: Assign the new data points to that category for which the number of the neighbor is
maximum.
 Step-6: Our model is ready.

10. Working of KNN
Continued
Suppose we have a new data point and we
need to put it in the required category.
Consider the following image:

11. Working of KNN
Continued
Firstly, we will choose the number of
neighbors, so we will choose the k=5.
Next, we will calculate the Euclidean
distance between the data points.

12. Working of KNN
Continued
 By calculating the Euclidean distance
we got the nearest neighbors, as three
nearest neighbors in category A and
two nearest neighbors in category B.
 As we can see the 3 nearest neighbors
are from category A, hence this new
data point must belong to category A

14. How to select the value of K in KNN
 Square Root of N rule: This rule offers a quick and practical way to
determine an initial k value for your KNN model.
Here, N represents the total number of data points in the dataset.
 Cross Validation Technique: we train different KNN models for different
values of K.
 Note: Normally we use the standard value of K=5

15. Overfitting and underfitting in KNN
A small value of K (number of nearest neighbors) could lead to
overfitting as well as a big value of k can lead to underfitting.
So choose the best value of K using Square Root of N rule.

16. Example
From the given data-set find
(x,y) = 170,57 whether belongs
to Under or Normal Weights

17. Solution
In this approach we are going to use
Euclidean distance formulae, n(no of
records)=9 and assuming K value as 3
d1 = sqrt ((x2-x1)² + (y2-y1)²)
x1=167,y1=51 and x2=170,y2=57
d1 = sqrt ((170–167)² + (57–51)²)
d1 = 6.7
d2 = sqrt ((x2-x1)² + (y2-y1)²)
x1=183,y1=56 and x2=170,y2=57
d2 = sqrt ((170–183)² + (57–56)²)
d2 = 13
d3 = sqrt ((x2-x1)² + (y2-y1)²)
x1=176,y1=69 and x2=170,y2=57
d3 = sqrt ((170–176)² + (57–69)²)
d3 = 13.04

18. • d4 = sqrt ((x2-x1)² + (y2-y1)²)
• x1=173,y1=64 and x2=170,y2=57
• d4 = sqrt ((170–173)² + (57–64)²)
• d4 = 7.6 • d5 = sqrt ((x2-x1)² + (y2-y1)²)
• x1=172,y1=65 and x2=170,y2=57
• d5 = sqrt ((170–172)² + (57–65)²)
• d5 = 8.2

19. • d6 = sqrt ((x2-x1)² + (y2-y1)²)
• x1=173,y1=64 and x2=170,y2=57
• d6 = sqrt ((170–173)² + (57–64)²)
• d6 = 7.61
• d7 = sqrt ((x2-x1)² + (y2-y1)²)
• x1=169,y1=58 and x2=170,y2=57
• d7 = sqrt ((170–169)² + (57–58)²)
• d7 = 1.414

20.  d8 = sqrt ((x2-x1)² + (y2-y1)²)
 x1=173,y1=57 and x2=170,y2=57
 d8 = sqrt ((170–173)² + (57–57)²)
 d8 = 3
 d9 = sqrt ((x2-x1)² + (y2-y1)²)
 x1=170,y1=55 and x2=170,y2=57
 d9 = sqrt ((170–170)² + (57–55)²)
 d9 = 2

21. Result
from above results D7, D8, D9 have minimum distance
(55,170) Normal-Weight, (57,173) Normal-Weight,(58,169) Normal-Weight.
→ → →
Hence out of three points three points are Normal-Weight.
Final Conclusion is given point is Normal-Weight

22. Advantages of KNN Algorithm
Simple to implement: KNN is a simple and easy-to implement
classification algorithm that requires no training.
Few Hyperparameters – The only parameters which are required in the training of a
KNN algorithm are the value of k and the choice of the distance metric which we
would like to choose from our evaluation metric.
Versatility: KNN can be used for both classification and regression problems.
Whether you need to perform binary classification or multi-class classification, the K-
nearest neighbor algorithm works well.

23. Advantages of KNN Algorithm con.
Non-parametric: The KNN algorithm does not make any assumptions about the
underlying data distribution, so it is well-suited for problems where the decision
boundary is non-linear.
 Handling missing values: KNN is less sensitive to missing values because the missing
values can simply be ignored when calculating the distance.
Handling outliers: KNN can be robust to outliers since the decision is based on the
majority class among k-nearest neighbors.

24. Disadvantages of the KNN Algorithm
Computationally expensive: KNN has a high computation cost during the prediction stage, especially
when dealing with large datasets. The algorithm needs to calculate the distance between the new data
point and all stored data points for each classification task. This can be slow and resource-intensive.
Memory-intensive: KNN stores all the training instances. This can require a large amount of memory
while dealing with large datasets.
High dimensionality: KNN may not work well when the number of features is high.
Not good with categorical variable: KNN is not good when the categorical variable is involved. It
works well when the variable is numerical.
Slow prediction: KNN is slow in prediction as it needs to calculate the distance of the new point from
each stored point. This is a slow process and computationally expensive

25. Applications of the KNN Classification Algorithm
Image recognition: We can use KNN classification to classify images based on their
content, such as recognizing handwritten digits or identifying objects in an image.
Medical diagnosis: We can use the KNN algorithm in medical diagnosis to classify
patients based on their symptoms or medical history.
Recommender systems: The recommender systems primarily use KNN classification
to make recommendations based on the similarity between users or items

26. Applications of the KNN Classification Algorithm cont.
Credit scoring: Banking applications can use the KNN classification algorithm to
classify loan applicants based on their credit history.
Speech recognition: You can use the KNN algorithm to classify speech sounds.
Quality control: You can use the KNN classification algorithm to classify items as
defective or non-defective based on their features.
Natural Language Processing (NLP): You can use the KNN algorithm for text
classification, such as sentiment analysis, spam detection, and topic classification