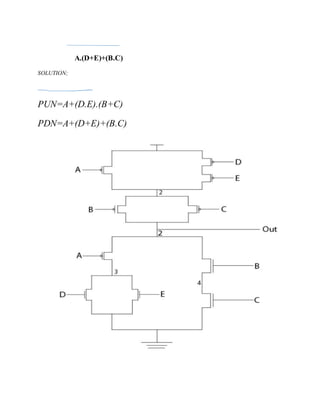
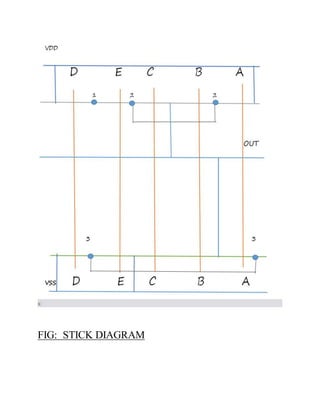
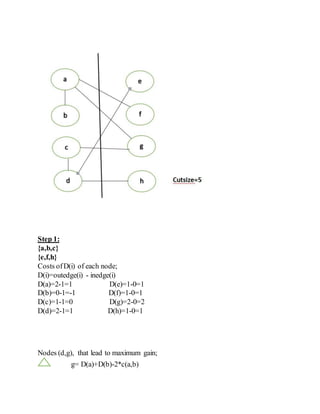
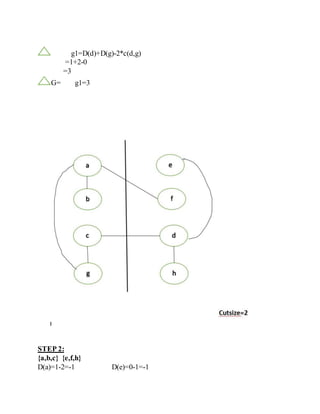
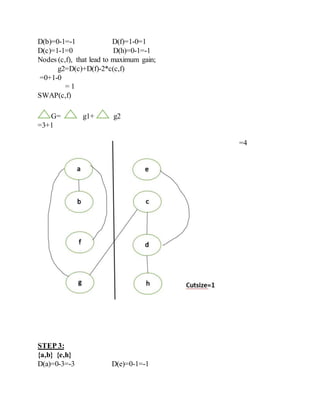
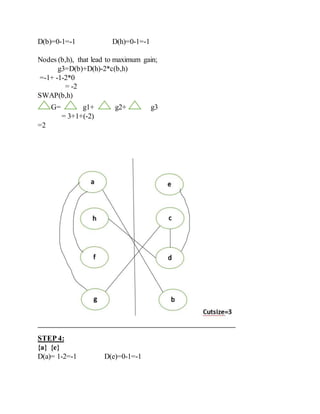
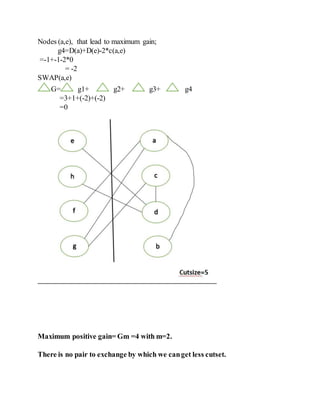
This document contains an assignment submission for a course on VLSI Design. It includes: 1) An explanation of stick diagrams and how they are constructed to visualize transistor placement and routing for a logic circuit. 2) An overview of the Kernighan-Lin algorithm for iterative partitioning of graphs to minimize cut size through pairwise exchange of nodes between partitions. 3) An example application of a single pass of the Kernighan-Lin algorithm on a sample circuit to demonstrate the process.

1. Ranada Prasad Shaha University
Department of Computer Science and Engineering
Date of Submission: 10/04/2018
Assignment No : 01
Assignment On : Stick diagram and KL algorithm
Course Name: VLSI Design.
Submitted By Submitted To
Name: Rubaiyyat Abir
ID: 15100002
Semester: 10
Dept of CSE, RPSU
MD. Mizanur Rahman
Lecturer
Dept of CSE, PRSU

2. Stick diagram
A stick diagram is a cartoon of a layout. Stick diagram are a means for the designer or engineers
to visualize the cell routing and transistor placement. The stick diagram reflects the relative
positions of components, but not their absolute positions or their sizes. Placement: Which
positions components will take. Routing: How runs wires between the components.
Method: Stick diagrams are constructed in few steps:
 The first step is to construct a logic graph of schematic diagram.
 Identify each transistor by a unique name of its gate signal (A, B, C, D, and
E).
 Then identify each connection to the transistor by a unique name (1, 2, 3
and 4).
 The second step is to construct one Euler path for both the Pull up and Pull down network.
 Euler paths are defined by a path the traverses each node in the path,
such that each edge is visited only once.
 The path is defined by the order of each transistor name. If the path
traverses transistor A then B then C. Then the path name is {A, B,
C}.
 The Euler path of the Pull up network must be the same as the path
of the Pull down network.
Q. Draw the stick diagram for the following network:

3. A.(D+E)+(B.C)
SOLUTION;
PUN=A+(D.E).(B+C)
PDN=A+(D+E)+(B.C)

4. FIG: STICK DIAGRAM

5. Kernighan-Lin Algorithm
Kernighan and Lin, “An efficient heuristic procedure for partitioning graphs".
It performs pair-wise exchange of nodes to reduce the cutsize.
An iterative, 2-way, balanced partitioning (bi-sectioning) heuristic.
Pair-wise interchange;
 Start with a placement: either generated at random or by some other algorithm.
 Repeatedly swap components to improve the placement. At each iteration select a pair of
components for consideration, if swapping their positions improves the costs , they are
swapped.
 Stop the iteration if there is no improvement.
Example:

6. Cost D(i) of moving nodes;
D(i)=outedge(i) - inedge(i)
Where,
Outedge(i)=number of lines that are cut by the cutline.
Inedge(i)=number of lines that are not cut by the cutline.
D(i)=amount by which the cutsize decreases if vertex I changes over other partition.
Gain of swapping a pair of nodes a,b
g= D(a)+D(b)-2*c(a,b)
 D(a),D(b) are the respective costs ofnodes a,b
 C(a,b) is the number of edges connected between a and b
Gm is compound as the sum of g values over the first m swaps of the
pass,mchosen suchthat Gm is maximum.
m
Gm=∑ g
i=1
Q. Perform a single KL pass on the following circuit:

7. Step 1:
{a,b,c}
{e,f,h}
Costs ofD(i) of each node;
D(i)=outedge(i) - inedge(i)
D(a)=2-1=1 D(e)=1-0=1
D(b)=0-1=-1 D(f)=1-0=1
D(c)=1-1=0 D(g)=2-0=2
D(d)=2-1=1 D(h)=1-0=1
Nodes (d,g), that lead to maximum gain;
g= D(a)+D(b)-2*c(a,b)

8. g1=D(d)+D(g)-2*c(d,g)
=1+2-0
=3
G= g1=3
STEP 2:
{a,b,c} {e,f,h}
D(a)=1-2=-1 D(e)=0-1=-1

9. D(b)=0-1=-1 D(f)=1-0=1
D(c)=1-1=0 D(h)=0-1=-1
Nodes (c,f), that lead to maximum gain;
g2=D(c)+D(f)-2*c(c,f)
=0+1-0
= 1
SWAP(c,f)
G= g1+ g2
=3+1
=4
STEP 3:
{a,b} {e,h}
D(a)=0-3=-3 D(e)=0-1=-1

10. D(b)=0-1=-1 D(h)=0-1=-1
Nodes (b,h), that lead to maximum gain;
g3=D(b)+D(h)-2*c(b,h)
=-1+ -1-2*0
= -2
SWAP(b,h)
G= g1+ g2+ g3
= 3+1+(-2)
=2
STEP 4:
{a} {e}
D(a)= 1-2=-1 D(e)=0-1=-1

11. Nodes (a,e), that lead to maximum gain;
g4=D(a)+D(e)-2*c(a,e)
=-1+-1-2*0
= -2
SWAP(a,e)
G= g1+ g2+ g3+ g4
=3+1+(-2)+(-2)
=0
Maximum positive gain= Gm =4 with m=2.
There is no pair to exchange by which we canget less cutset.