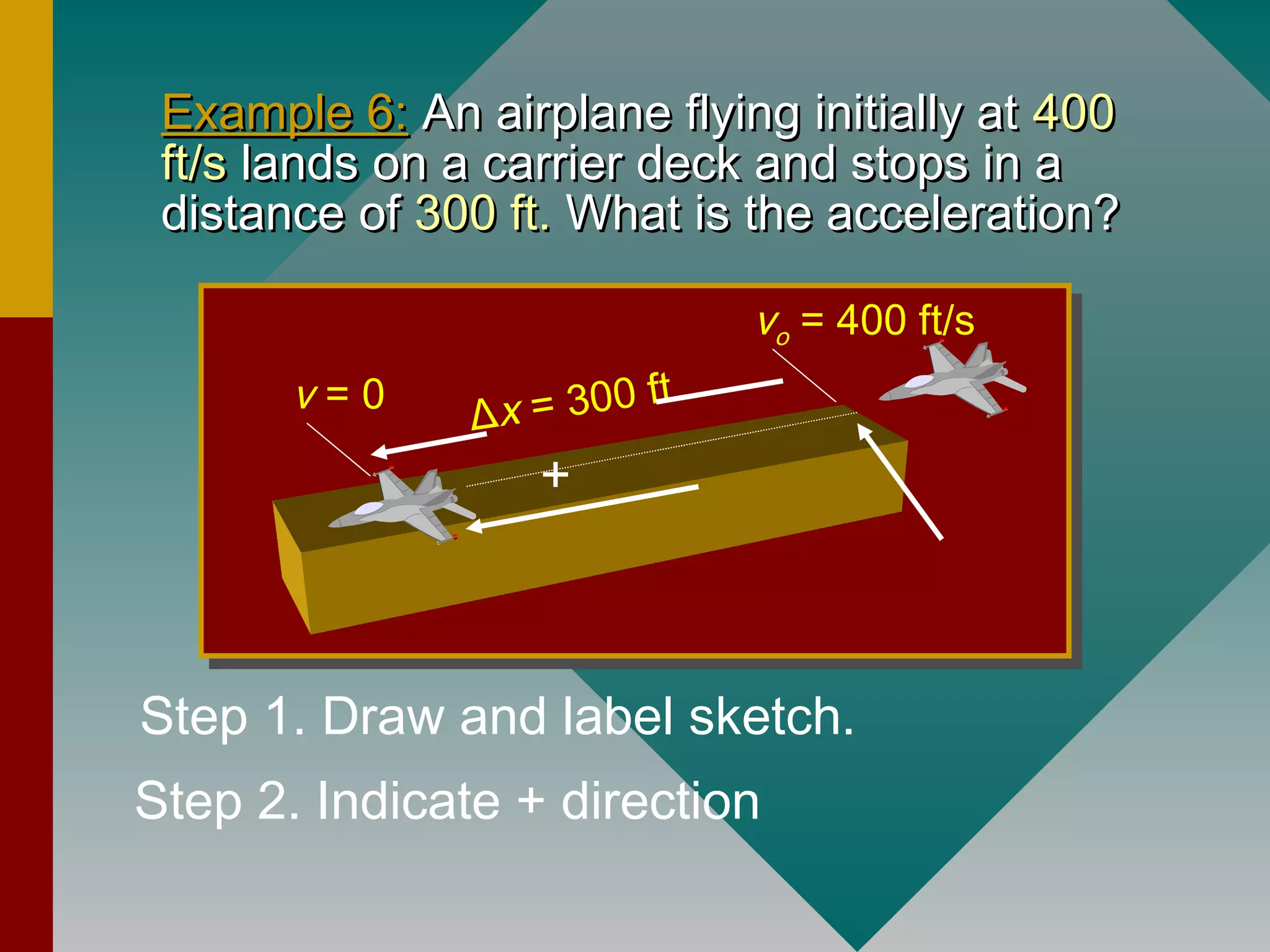
The document discusses kinematics concepts including distance, displacement, speed, velocity, and acceleration. It defines distance as the total length of a path traveled and displacement as the straight-line distance between initial and final positions. Speed is the distance traveled per unit time and is a scalar quantity, while velocity is displacement per unit time and has both magnitude and direction. Acceleration is the rate of change of velocity with respect to time and occurs when a force acts on an object. Formulas for average and instantaneous velocity and acceleration are presented for motion with constant acceleration. Examples apply these concepts to problems involving cars, runners, airplanes, and balls on inclines.

1. Kinematics in OneKinematics in One
DimensionDimension

2. The CheetahThe Cheetah: A cat that is built for speed. Its strength and: A cat that is built for speed. Its strength and
agility allow it to sustain a top speed of over 100 km/h. Suchagility allow it to sustain a top speed of over 100 km/h. Such
speeds can only be maintained for about ten seconds.speeds can only be maintained for about ten seconds.

3. Distance and DisplacementDistance and Displacement
Distance is the length of the actual path
taken by an object. Consider travel from
point A to point B in diagram below:
Distance is the length of the actual path
taken by an object. Consider travel from
point A to point B in diagram below:
A
B
d = 20 m
DistanceDistance dd is ais a scalarscalar
quantity (no direction):quantity (no direction):
ContainsContains magnitudemagnitude onlyonly
and consists of aand consists of a
numbernumber and aand a unit.unit.

4. Distance and DisplacementDistance and Displacement
DisplacementDisplacement is the straight-line separationis the straight-line separation
of two points in a specified direction.of two points in a specified direction.
DisplacementDisplacement is the straight-line separationis the straight-line separation
of two points in a specified direction.of two points in a specified direction.
A vector quantity:
Contains magnitude
AND direction, a
number, unit & angle.
A
BΔs = 12 m, 20o
θ

5. Distance and DisplacementDistance and Displacement
• For motion along x or y axis, theFor motion along x or y axis, the displacementdisplacement isis
determined by the x or y coordinate of its final position.determined by the x or y coordinate of its final position.
Example: Consider a car that travels 8 m, E then 12Example: Consider a car that travels 8 m, E then 12
m, W.m, W.
• For motion along x or y axis, theFor motion along x or y axis, the displacementdisplacement isis
determined by the x or y coordinate of its final position.determined by the x or y coordinate of its final position.
Example: Consider a car that travels 8 m, E then 12Example: Consider a car that travels 8 m, E then 12
m, W.m, W.
Net displacementNet displacement ΔxΔx
is from the origin tois from the origin to
the final position:the final position:
What is theWhat is the distancedistance
traveled?traveled? d = 20 m !!
12 m,W
Δ
x
Δx = 4 m, WΔx = 4 m, W
x
8 m,E
x = +8x = -4

6. Definition of SpeedDefinition of Speed
• SpeedSpeed is the distance traveled per unit ofis the distance traveled per unit of
time (a scalar quantity).time (a scalar quantity).
• SpeedSpeed is the distance traveled per unit ofis the distance traveled per unit of
time (a scalar quantity).time (a scalar quantity).
vs = =
d
t
20 m
4 s
vs = 5 m/svs = 5 m/s
Not direction dependent!
A
Bd = 20 m
Time t = 4 s

7. Definition of VelocityDefinition of Velocity
• VelocityVelocity is the displacement peris the displacement per
unit of time. (A vector quantity.)unit of time. (A vector quantity.)
• VelocityVelocity is the displacement peris the displacement per
unit of time. (A vector quantity.)unit of time. (A vector quantity.)
Direction required!
A
Bs = 20 m
Time t = 4 s
Δx=12 m
20o
= 3 m/s at 200
N of E= 3 m/s at 200
N of E

8. Average Speed andAverage Speed and
Instantaneous VelocityInstantaneous Velocity
The instantaneous
velocity is the magn-
itude and direction of
the velocity at a par-
ticular instant. (v at
point C)
The instantaneous
velocity is the magn-
itude and direction of
the velocity at a par-
ticular instant. (v at
point C)
 TheThe averageaverage speedspeed dependsdepends ONLYONLY onon
the distance traveled and the timethe distance traveled and the time
required.required.
 TheThe averageaverage speedspeed dependsdepends ONLYONLY onon
the distance traveled and the timethe distance traveled and the time
required.required.
A
Bs = 20 m
Time t = 4 s
C

9. Example 1.Example 1. A runner runsA runner runs 200 m, east,200 m, east, thenthen
changes direction and runschanges direction and runs 300 m, west300 m, west. If the. If the
entire trip takesentire trip takes 60 s60 s, what is the average, what is the average
speed and what is the average velocity?speed and what is the average velocity?
Recall thatRecall that averageaverage
speedspeed is a functionis a function
onlyonly ofof total distancetotal distance
andand total timetotal time::
Total distance:Total distance: ss = 200 m + 300 m = 500 m= 200 m + 300 m = 500 m
500 m
60 s
total path
Average speed
time
= =
Avg. speed= 8 m/s Direction does not matter!Direction does not matter!
startstart
ss11 = 200 m= 200 mss22 = 300 m= 300 m

10. Example 1 (Cont.)Example 1 (Cont.) Now we find the averageNow we find the average
velocity, which is thevelocity, which is the net displacementnet displacement divideddivided
byby timetime. In this case, the direction matters.. In this case, the direction matters.
xxoo = 0= 0
tt = 60 s= 60 s
xx11 = +200 m= +200 mxx = -100 m= -100 m
xxoo = 0 m;= 0 m; xx = -100 m= -100 m
Direction of finalDirection of final
displacement is todisplacement is to
the left as shown.the left as shown.
Average velocity:
Note: Average velocity is directed to the west.Note: Average velocity is directed to the west.

11. Definition of AccelerationDefinition of Acceleration
 AnAn accelerationacceleration is the change in velocityis the change in velocity
per unit of time. (Aper unit of time. (A vectorvector quantity.)quantity.)
 AA changechange inin velocityvelocity requires therequires the
application of a push or pull (application of a push or pull (forceforce).).
A formal treatment of force and acceleration willA formal treatment of force and acceleration will
be given later. For now, you should know that:be given later. For now, you should know that:
• The direction of accel-
eration is same as
direction of force.
• The acceleration is
proportional to the
magnitude of the force.

12. Pulling the wagon with twice the forcePulling the wagon with twice the force
produces twice the acceleration andproduces twice the acceleration and
acceleration is in direction of force.acceleration is in direction of force.
Pulling the wagon with twice the forcePulling the wagon with twice the force
produces twice the acceleration andproduces twice the acceleration and
acceleration is in direction of force.acceleration is in direction of force.
Acceleration and ForceAcceleration and Force
F
a
2F 2a

13. Example 3 (No change in direction):Example 3 (No change in direction): A constantA constant
force changes the speed of a car fromforce changes the speed of a car from 8 m/s8 m/s toto
20 m/s20 m/s inin 4 s4 s. What is average acceleration?. What is average acceleration?
Step 1. Draw a rough sketch.Step 1. Draw a rough sketch.
Step 2. Choose a positive direction (right).Step 2. Choose a positive direction (right).
Step 3. Label given info with + and - signs.Step 3. Label given info with + and - signs.
Step 4. Indicate direction of force F.Step 4. Indicate direction of force F.
+
vo = +8 m/s
t = 4 s
v = +20 m/s
Force

14. Example 3 (Continued):Example 3 (Continued): What is averageWhat is average
acceleration of car?acceleration of car?
Step 5. Recall definitionStep 5. Recall definition
of average acceleration.of average acceleration.
+
vo = +8 m/s
t = 4 s
v = +20 m/s
Force

15. Graphical AnalysisGraphical Analysis
slope:slope:
velocity:velocity:
acceleration:acceleration:

16. x, (m)x, (m)
Position vs time graph (velocity)Position vs time graph (velocity)

17. v, (m/s)v, (m/s)
velocity vs time graph (acceleration)velocity vs time graph (acceleration)

18. Graphical AnalysisGraphical Analysis
∆x
∆∆tt
xx22
xx11
tt22tt11
2 1
2 1
avg
x x x
v
t t t
∆ −
= =
∆ −
( 0)inst
x
v t
t
∆
= ∆ →
∆
∆x
∆t
Time
slope
Displacement,x
Average Velocity:Average Velocity: Instantaneous Velocity:Instantaneous Velocity:

19. Uniform AccelerationUniform Acceleration
in One Dimension:in One Dimension:
• Motion is along a straight line (horizontal,Motion is along a straight line (horizontal,
vertical or slanted).vertical or slanted).
• Changes in motion result from aChanges in motion result from a
CONSTANT force producing uniformCONSTANT force producing uniform
acceleration.acceleration.
• The velocity of an object is changing by aThe velocity of an object is changing by a
constant amount in a given time interval.constant amount in a given time interval.
• The moving object is treated as though itThe moving object is treated as though it
were a point particle.were a point particle.

20. Average velocity for constant a:
setting to = 0
combining both equations:
For constant acceleration:

21. Formulas based on definitionsFormulas based on definitions::
DerivedDerived formulasformulas:
For constant acceleration onlyFor constant acceleration only

22. Example 6:Example 6: An airplane flying initially atAn airplane flying initially at 400400
ft/sft/s lands on a carrier deck and stops in alands on a carrier deck and stops in a
distance ofdistance of 300 ft.300 ft. What is the acceleration?What is the acceleration?
Δx = 300 ft
vo = 400 ft/s
v = 0
+
Step 1. Draw and label sketch.
Step 2. Indicate + direction

23. Example: (Cont.)Example: (Cont.)
+
Step 3.Step 3. List given; find information with signs.
Given:Given: vvoo = 400 ft/s= 400 ft/s - initial velocity of airplane- initial velocity of airplane
vv = 0= 0 - final velocity after- final velocity after
travelingtraveling ΔΔxx = +300 ft= +300 ft
Find:Find: aa = ?= ? - acceleration of airplane- acceleration of airplane
Δx = 300 ft
vo = 400 ft/s
v = 0

24. Step 4.Step 4. Select equation
that contains aa and not tt.
v 2 - vo
2 = 2aΔx
0
a = =
-vo
2
2x
-(400 ft/s)2
2(300 ft)
aa = - 300 ft/s= - 300 ft/s22aa = - 300 ft/s= - 300 ft/s22
Why is the acceleration negative?Why is the acceleration negative?Because Force is in a negative direction whichBecause Force is in a negative direction which
means that the airplane slows downmeans that the airplane slows down
Given:Given: vvoo = +400 ft/s= +400 ft/s
vv = 0= 0
ΔΔxx = +300 ft= +300 ft

25. Example 5:Example 5: A ballA ball 5.0 m5.0 m from the bottom of anfrom the bottom of an
incline is traveling initially atincline is traveling initially at 8.0 m/s8.0 m/s. Four. Four
secondsseconds (4.0 s)(4.0 s) later, it is traveling down thelater, it is traveling down the
incline atincline at 2.0 m/s2.0 m/s. How far is it from the bottom at. How far is it from the bottom at
that instant?that instant?
5.0 m
Δx
8.0 m/s
-2.0 m/s
t = 4.0 s
+
Given:Given: dd = 5.0 m= 5.0 m - distance from initial position of the ball
vvoo = 8.0 m/s= 8.0 m/s - initial velocityvelocity
vv = -2.0 m/s= -2.0 m/s - final velocity after- final velocity after tt = 4.0 s= 4.0 s
Find:Find: xx = ?= ? -- distance from the bottom of the inclinedistance from the bottom of the incline

26. x = 17.0 mx = 17.0 m
Given:Given: dd = 5.0 m= 5.0 m
vvoo = 8.0 m/s= 8.0 m/s - initial velocityvelocity
vv = -2.0 m/s= -2.0 m/s - final velocity after- final velocity after tt = 4.0 s= 4.0 s
Find:Find: xx = ?= ? -- distance from the bottom of the inclinedistance from the bottom of the incline
Solution:Solution: wherewhere

27. Acceleration Due to GravityAcceleration Due to Gravity
• Every object on the earthEvery object on the earth
experiences a common force:experiences a common force:
the force due to gravity.the force due to gravity.
• This force is always directedThis force is always directed
toward the center of the earthtoward the center of the earth
(downward).(downward).
• The acceleration due to gravity isThe acceleration due to gravity is
relatively constant near therelatively constant near the
Earth’s surface.Earth’s surface.
• Every object on the earthEvery object on the earth
experiences a common force:experiences a common force:
the force due to gravity.the force due to gravity.
• This force is always directedThis force is always directed
toward the center of the earthtoward the center of the earth
(downward).(downward).
• The acceleration due to gravity isThe acceleration due to gravity is
relatively constant near therelatively constant near the
Earth’s surface.Earth’s surface.
Earth
Wg

28. Gravitational AccelerationGravitational Acceleration
• In a vacuum, all objects fallIn a vacuum, all objects fall
with same acceleration.with same acceleration.
• Equations for constantEquations for constant
acceleration apply as usual.acceleration apply as usual.
• Near the Earth’s surface:Near the Earth’s surface:
• In a vacuum, all objects fallIn a vacuum, all objects fall
with same acceleration.with same acceleration.
• Equations for constantEquations for constant
acceleration apply as usual.acceleration apply as usual.
• Near the Earth’s surface:Near the Earth’s surface:
aa = g = -= g = -9.80 m/s9.80 m/s22
or -32 ft/sor -32 ft/s22
Directed downward (usually negative).Directed downward (usually negative).

29. Sign Convention:Sign Convention:
A Ball ThrownA Ball Thrown
Vertically UpwardVertically Upward
• Velocity is positive (+) orVelocity is positive (+) or
negative (-) based onnegative (-) based on
direction of motiondirection of motion..
• Velocity is positive (+) orVelocity is positive (+) or
negative (-) based onnegative (-) based on
direction of motiondirection of motion..
• Displacement is positive (+)Displacement is positive (+)
or negative (-) based onor negative (-) based on
LOCATIONLOCATION..
• Displacement is positive (+)Displacement is positive (+)
or negative (-) based onor negative (-) based on
LOCATIONLOCATION..
Release
Point
UP = +
• Acceleration is (+) or (-)Acceleration is (+) or (-)
based on direction ofbased on direction of forceforce
(weight).(weight).
y = 0
y = +
y = +
y = +
y = 0
y =
-NegativeNegative
v = +
v = 0
v = -
v = -
v=
-NegativeNegative
a = -
a = -
a = -
a = -
a = -a = -

30. Example 7:Example 7: A ball is thrown vertically upward withA ball is thrown vertically upward with
an initial velocity ofan initial velocity of 30.0 m/s30.0 m/s. What are its position. What are its position
and velocity afterand velocity after 2.00 s2.00 s,, 4.00 s4.00 s, and, and 7.00 s7.00 s? Find? Find
also the maximum height attainedalso the maximum height attained
a = g
+
vo = +30.0 m/s
Given:Given: aa = -= -ΔΔ9.8 m/s9.8 m/s22
vvoo = 30.0 m/s= 30.0 m/s
tt = 2.00 s; 4.00 s; 7.00 s= 2.00 s; 4.00 s; 7.00 s
Find:Find:
ΔΔyy = ? – displacement= ? – displacement
vv = ? - final velocity= ? - final velocity
After those three “times”After those three “times”
ΔΔyy = ? – maximum height= ? – maximum height

31. Given:Given: aa = -9.8 m/s= -9.8 m/s22
;; vvoo = 30.0 m/s= 30.0 m/s
tt = 2.00 s; 4.00 s; 7.00 s= 2.00 s; 4.00 s; 7.00 s
Solutions:Solutions:
ForFor tt = 2.00 s:= 2.00 s:
ForFor tt = 4.00 s:= 4.00 s:
ForFor tt = 7.00 s:= 7.00 s:

32. Given:Given: aa = -9.8 m/s= -9.8 m/s22
;; vvoo = 30.0 m/s= 30.0 m/s
tt = 2.00 s; 4.00 s; 7.00 s= 2.00 s; 4.00 s; 7.00 s
Solutions:Solutions:
ForFor tt = 2.00 s:= 2.00 s:
ForFor tt = 4.00 s:= 4.00 s:
ForFor tt = 7.00 s:= 7.00 s:

33. Given:Given: aa = -9.8 m/s= -9.8 m/s22
;; vvoo = 30.0 m/s= 30.0 m/s
tt = 2.00 s; 4.00 s; 7.00 s= 2.00 s; 4.00 s; 7.00 s
Solutions:Solutions:
For maximum height,For maximum height, vv = 0 (the ball stops at= 0 (the ball stops at
maximum height):maximum height):

34. Experiment 10Experiment 10
Uniformly Accelerated MotionUniformly Accelerated Motion
(Acceleration due to Gravity) 39(Acceleration due to Gravity) 39
(06A)(06A)