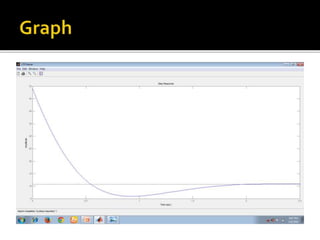
This document discusses open loop control systems and their transfer functions. It defines open loop systems as those without feedback, and describes their basic elements and properties. The document then defines the transfer function as the ratio of the Laplace transforms of the output and input quantities. It explains that the transfer function provides information about the system's gain and converts differential equations to algebraic equations. The transfer function depends on system parameters but not inputs. Zeros and poles are also defined as the roots of the numerator and denominator polynomials. System stability depends on the location of poles in the complex plane. Examples of transfer function calculations and analyses are provided.

1. CAREER POINT
UNIVERSITY
MAJOR ASSIGNMENT
ON
Design and analysis of
open loop transfer function

2.  In modern era , control system play a vital role
in human life.A control system is an
interconnection of component forming a
system configuration in which any quantity of
interest or altered in accordance with a desired
manner.The basic control system are :
 Input
 Control system
 output

3.  Definition
 Without feedback or non feed back control
system is known as open loop control system.
 The element of an open loop control system
can usually be divided into two parts:
The actuating device
The controlled process

4.  Open loop control systems are simple in
construction.
 Open loop control system in cheap.
 Generally the open loop systems are stable.
 The maintenance required for open loop
system is less.
 Calibration of open loop control system is
easily.

5.  Open loop system are inaccurate.The
accuracy is depend up on the calibration of
input.
 The open loop systems are not reliable, the
operation of these is affected due to the
presence of non linearties in its element.
 Optimization of open loop system is not
possible.

6.  “The transfer function is define as the ratio of
the Laplace transform of the output quantity
to the Laplace transform of the input
quantity, with all initial condition assumed to
the zero.”
Then the transfer function is
Transfer function=output/input
G(s)=Y(s)/R(s)

7. G(S)=Y(S)/R(S)
R(S) G(s) Y(s)

8.  Its provide the gain of the system.
 Integral and differential equation are
converted to algebraic equation.
 The transfer function is dependent on the
parameters of the system and independent of
the system.
 If transfer function G(s) is known than any
output for any given input , can be known.

9.  Transfer function can be calculated only for
linear and time invariant system.
 Consider only when initial condition are zero.
 Its does not give any information about
physical structure of the system.

10.  Zeros are defined as the root of the
polynomial of the numerator of the transfer
function.
 Poles are the defined as the root of the
polynomial of the denominator of the
transfer function.

11.  The value of s which are substitued in the
denominator of the transfer function after
substituting the value of y the transfer
function becomes “infinite “, these values are
called poles of the transfer function.
Like P1,P2,------Pn are those value which
makes the transfer function infinite when
substitute in previous equation.

12.  The value of s which are substituted in the
numerator of the transfer function, after
substituting the value, the transfer function
becomes “Zeros” these values are the called
zeros of the transfer function.
Like Z1,Z2,--------Zn are those value which
makes the transfer function zero.

13.  When the value of poles and zeros are not
repeated , such poles and zeros are called
simple poles and zeros . If repeated such
poles and zeros are called multiple poles and
zeros .
 The order of repeated pole and zeros is equal
to the number of times they are repeated.

14.  If all the poles of the system lie in left half
plane the system is said to be Stable.
 If any of the poles lie in right half plane the
system is said to be unstable.
 If pole(s) lie on imaginary axis the system is
said to be marginally stable.

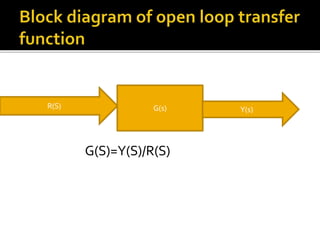
15.  P1=[8 56 96];
 Q1=[1 4 9 10];
 Sys=tf(P1,Q1)
 Roots(P1);
 Roots(Q1);
 pzMAP(sys);

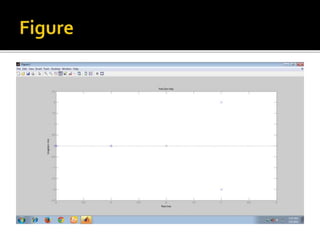
17.  Num=[49];
 Den=[ 1 4 9 ];
 Sys=tf(num,den);
 load ltiexamples
 ltiview

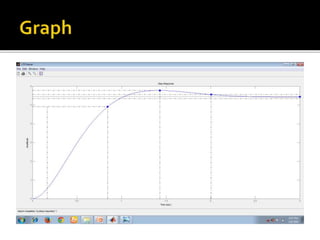
19.  Num=[49 89 96];
 Den=[1 4 9];
 Sys=tf[Num,Den];
 Load ltiexamples
 ltiview