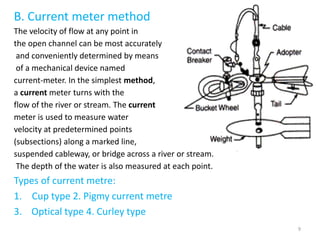
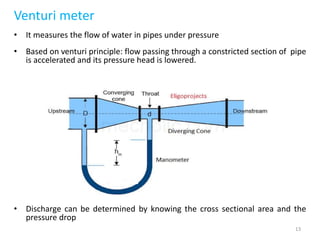
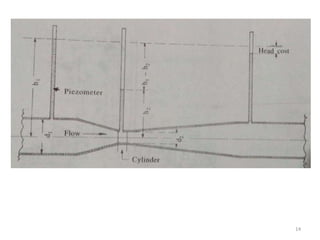
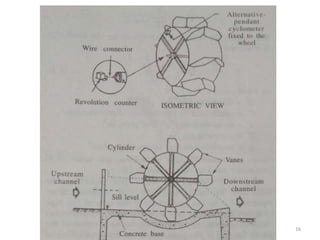
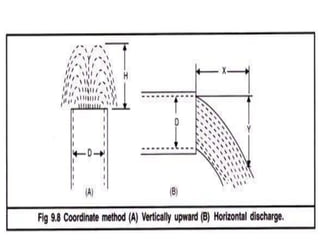
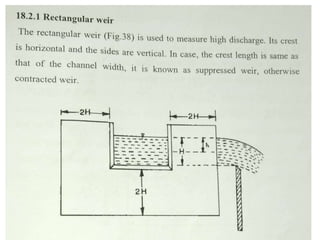
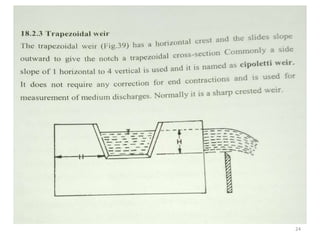
Irrigation water measurement is essential for determining how much water to apply to crops and for field experiments. Water can be measured by volume per unit of time for flowing water, or by total volume for stationary water. Common units include cubic meters per second. Accurate measurement requires choosing an appropriate technique depending on the volume of water, desired accuracy, and financial resources. Methods include the direct volumetric method, velocity-area method using floats or current meters, water meters, venturi meters, and tracer techniques.

1. 1
Irrigation Water Measurement
Speaker
Dr. Jitendra Sinha, Associate Professor
Department of Soil and Water Engineering,
SVCAETRS, FAE, IGKV, Raipur
jsvenusmars@gmail.com, 7000633581

2. • Irrigation water management begins with knowing how
much water is available for irrigation
Why water measurement is required?
• To determine the amount of water to be applied to
the crops.
• Accurate measurement of irrigation water is necessary
in field experiments on soil-water-plant relationship.
• Required in testing wells for their yield
What is the unit of measurement of water?
• Water in motion; i.e., flowing in streams, canals, pipe-
lines, and ditches, is measured in units of volume per
unit of time— cubic metre per second (cumec), cubic
feet per second (cusec), litres per second (lps) etc.
• Water at rest: measured in volume; like capacity of
pond, capacity of a tank, capacity of dam etc. 2

3. 1. A Persian wheel discharges at the rate of 11,000 litres per
hour and works for eight hours each day. Estimate the area
commanded by the water lift if the average depth of
irrigation is 8 cm and irrigation interval is 15 days.
Solution:
• The discharge of Persian wheel in 15 days
• =
11,000 × 8 × 15
1000
= 1320 m3
• Water required to cover one hectare to a depth of 8 cm
• = 10,000 ×
8
100
= 800 m3
• Area commanded by Persian wheel
• =
Water available
Water required per unit area
• =
1320
800
= 1.65 hectares.
3

4. 2. Compute the efficiency of an irrigation system based on
the following data: 1800 litres / min of water is diverted to
the farm each day of 24 hrs. Each day 0.8 ha of maize and 1
ha wheat are irrigated. The irrigation requirement of maize is
8 cm and that of wheat 12 cm.
Solution: S = 1800 litres / min =
(1800 × 60 ×24)
1000
= 2592 cubic meters
Volume of water required to irrigate maize
= (
8
100
) × 0.8 × 1000 = 640 cubic meters
Volume of water required to irrigate wheat
= (
12
100
) × 1 × 1000 = 1200 cubic meters
Total water use by maize and wheat
= 640 + 1200 = 1840 cubic meters
• Ei = (
1840
2592
) × 100 = 70.99%, say 71%.
4

5. • Methods of measuring irrigation water can be
grouped into four basic categories—
1. Direct or volumetric method
2. Velocity-area method
3. Constricted flow
4. Tracer technique
• Choice of method to use will be determined by
the volume of water to be measured, the
degree of accuracy desired, whether the
installation is permanent or temporary, and the
financial investment required.
5

6. • Direct or Volumetric Measurement Methods
(1) Measuring the period of time required to fill a container of a
known volume can be used to measure small rates of flow such as
from individual siphon tubes, sprinkler nozzles, or from individual
outlets in gated pipe. Ordinarily 20 to 200 litres containers will be
adequate. It is recommended that the measurement be repeated at
least three times and preferably five times to arrive at a reliable rate
of flow per unit of time.
6Source: Irrigation Theory and Practice, AM Michael

7. 2. Velocity-area method : The rate of flow passing
a point in pipe or open channel is determined by
multiplying the cross sectional area of the flow
section at right angles to the direction of flow by
the average velocity of water
Q = A x V
Q = Discharge rate, m3s-1
A = Area of cross section of channel or pipe, m2
V = Velocity of flow, ms-1
7

8. A. Float method
The float method can be used to obtain an approximate measure of the
rate of flow occurring in an open ditch. It is especially useful where more
expensive installations are not justified or high degree accuracy is not
required.
Select a straight section of ditch from 20 to 30 m long with fairly uniform
cross-sections. Make several measurements of the width and depth of
the test cross-section so as to arrive at an average cross-sectional area.
Using a tape, measure the length of the test section of the ditch. Place a
small floating object in the ditch a few metres above the starting point of
the test section and time the number of seconds for this object to travel
the length of the test section. This time measurement should be made
several times to arrive at a reliable average value. By dividing the length
of the test section (metres) by the average time required (seconds), one
can estimate velocity in metre per second. Since the velocity of water at
the surface is greater than the average velocity of the stream, multiply
the estimated surface velocity by a correction factor (0.80 for smooth
lined ditches, and 0.60 for rough ditches) to obtain the average stream
velocity. To obtain the rate of flow, multiply the average cross sectional
area of the ditch (square metre) times the stream velocity (metres per
second) and the answer is the rate of flow in cubic metres per second.
8

9. B. Current meter method
The velocity of flow at any point in
the open channel can be most accurately
and conveniently determined by means
of a mechanical device named
current-meter. In the simplest method,
a current meter turns with the
flow of the river or stream. The current
meter is used to measure water
velocity at predetermined points
(subsections) along a marked line,
suspended cableway, or bridge across a river or stream.
The depth of the water is also measured at each point.
Types of current metre:
1. Cup type 2. Pigmy current metre
3. Optical type 4. Curley type
9

10. 1. Cup type current meter
• Also called rotating type
• Flow velocity is proportional to the revolution of the wheel
• No. of revolutions re recorded by an electrical circuit
2. Pigmy type
• Miniature type current metre
• Design and construction similar to curley type current meter
• Most suitable when velocity (< 1 ms-1) and depth of flow are less.
3. Optical current meter
• It is a stroboscopic device used for measuring flow velocity
without immersing into water
• Consists of light weight battery, low power telescope, rotating
mirror, motor and tachometer
4. Curley current meter
• Price current meter
• It consists of head, tail, hanger, recorder and suspended device
10

11. Rating of current meter:
• Development of a relationship between the number of
revolutions per minute and the flow velocity
• The equation is called rating equation
• Rating equation is provided by the manufacturer
• V = aN + b
V = Velocity of flow (ms-1)
N = Revolutions per second
‘a’ and ‘b’ are constants provided in the rating equation
• Mean velocity is taken as average value associated with 0.2 and
0.8 depth of flow
11

12. Water meter: These water meters are used to measure the
total flow of water passing
through pipeline in mining,
waterworks and industrial
enterprises.
• It utilises multi blade
Conical propeller made of metal,
Plastic or rubber, rotating in a
Vertical plane and geared to a
totalizer in such manner that a
Numerical counter can
totalise the flow in any desired
volumetric units.
12

13. Venturi meter
• It measures the flow of water in pipes under pressure
• Based on venturi principle: flow passing through a constricted section of pipe
is accelerated and its pressure head is lowered.
• Discharge can be determined by knowing the cross sectional area and the
pressure drop
13

14. 14

15. 15

16. 16

17. 17

18. Coordinate Method:
• It measures the jet or water issuing from the end of the pipe
for calculating rate of discharge. Flow from pipes may be
measured whether the pipe is discharging vertically upward,
horizontally or at some angle with the horizontal. Coordinate
methods are used to measure the flow from small pumping
plants discharging horizontally and from flowing wells
discharging vertically. These methods have limited accuracy
owing to problems in making accurate measurements of
coordinate of the jet.
• To measure the flow from pipes discharging vertically upward,
it is necessary to measure inside dia D of the pipe and the
height H of the jet above the pipe outlet .
• To measure the flow from pipes discharging horizontally, it is
necessary to measure both horizontal and vertical distance
from the point on the jet.
• For instance, coordinates are measured from the top of the
inside of the pipe to a point on the top of the jet. These
horizontal and vertical distances are called X and Y ordinates,
respectively. 18

19. 19

20. • The formula used is obtained by combining the
following equations:
• Q = A × V
• X = V × t or V = X/t
• Y = ½ × gt2 or t = √2Y/g
• Introducing C, the coefficient of discharge, we
have
• Q = C × A × X × √g/2Y
• The above equation can be written as
• where, Q is in lps, X and Y measured in cm, A in
cm2 and g taken as 980 cm s-1. Discharge can be
obtained from standard tables. 20

21. 21The Tracer Technique

22. 22

23. 23

24. 24

25. 25

26. 26

27. 27

28. 28

29. 29

30. 30

31. 31

32. 32

33. 33

34. 34

35. 35

36. REFERENCES
• Irrigation:
Theory and Practice: AM Michael
• Reference notes: Course no. AENG 151,
Fundamentals of Soil and Water Conservation
Engineering, ANGRAU
• http://www.agricultureinindia.net/wp-content

37. Be Indian
Buy Indian

38. 38
?
THANK YOU