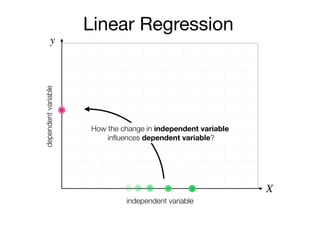
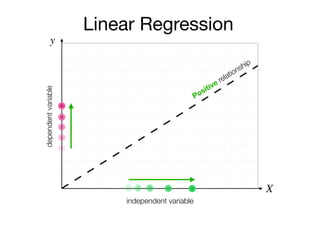
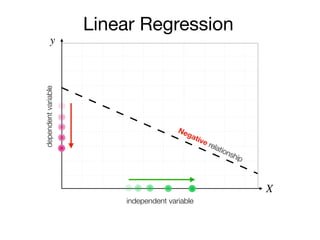
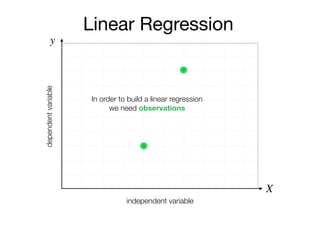
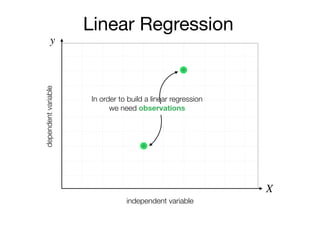
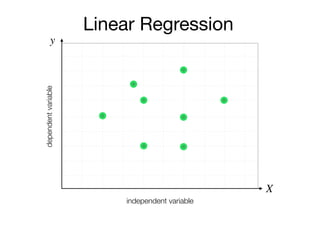
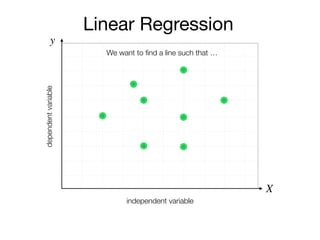
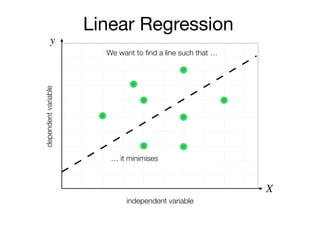
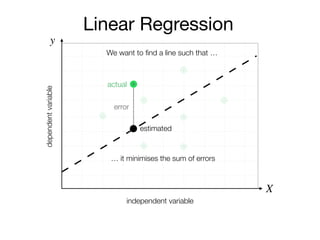
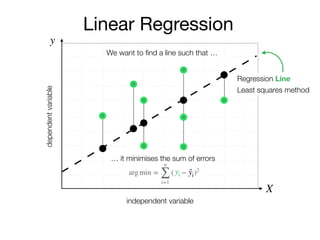
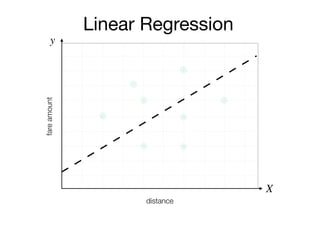
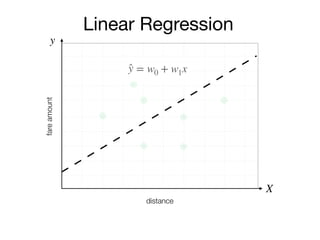
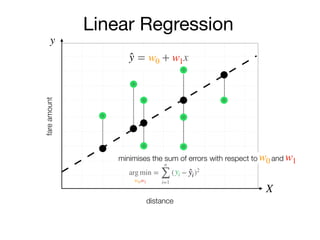
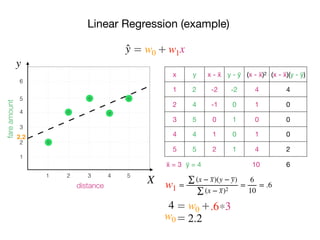
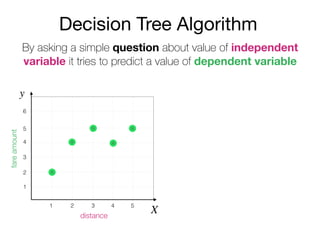
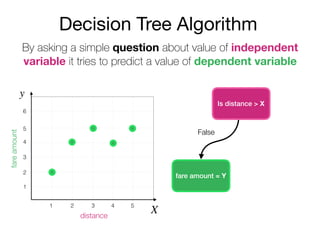
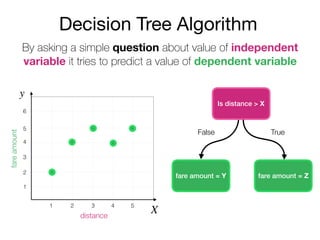
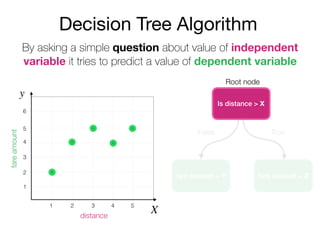
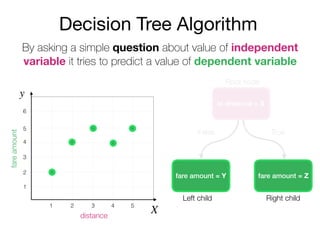
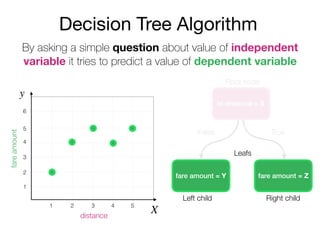
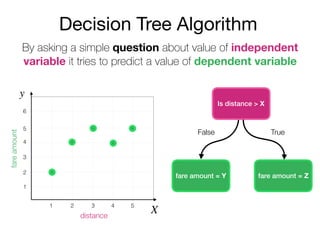
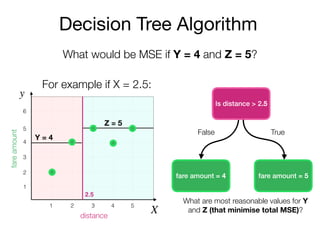
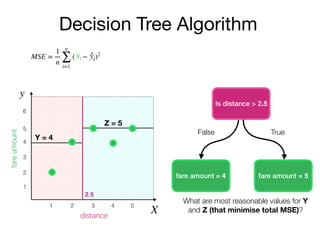
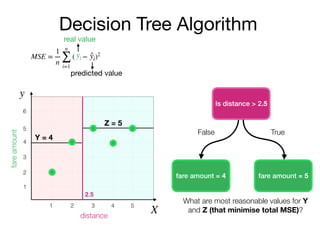
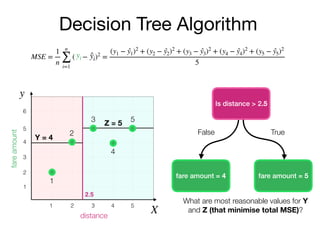
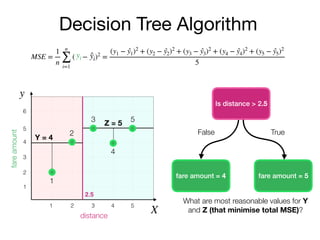
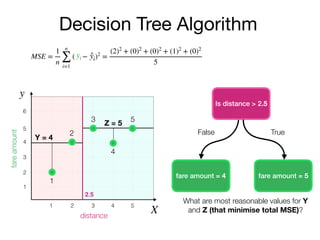
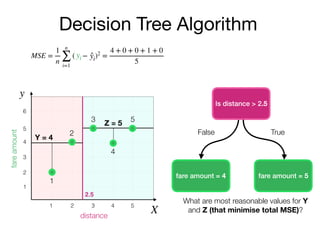
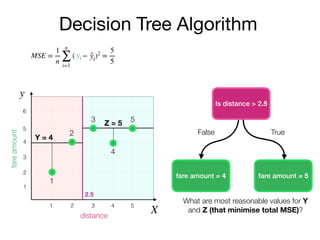
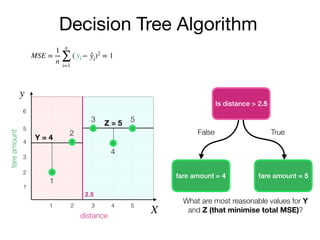
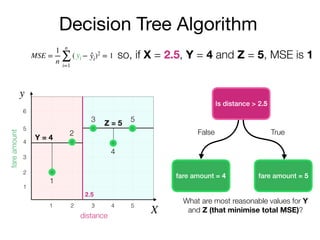
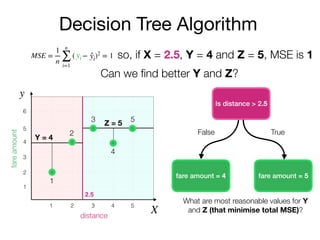
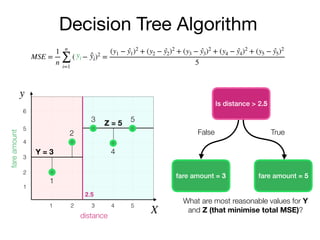
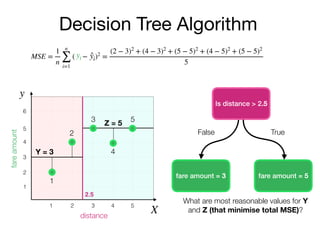
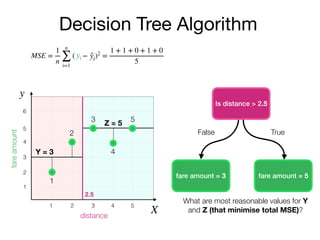
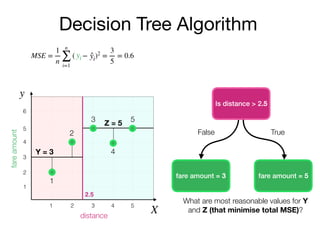
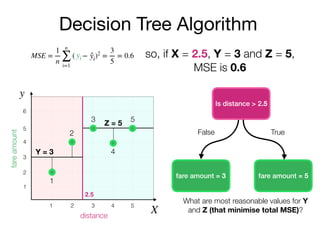
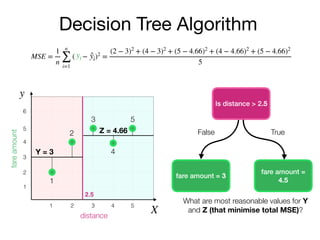
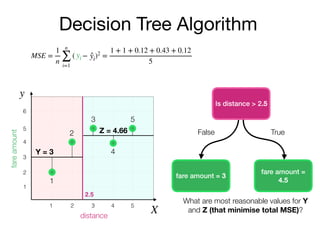
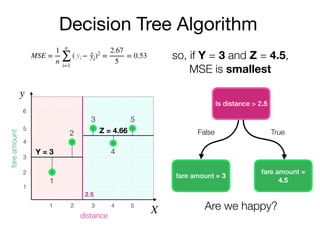
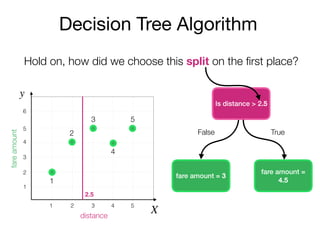
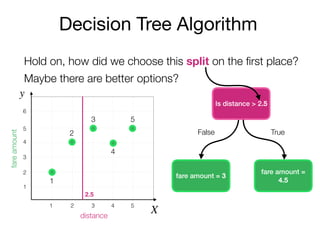
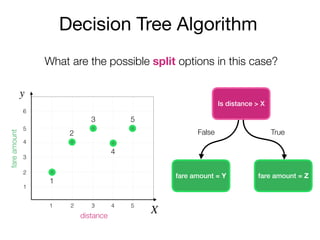
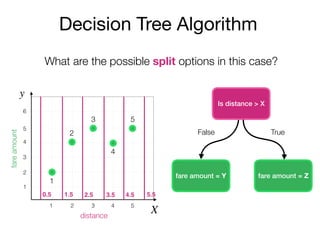
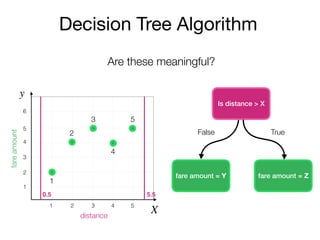
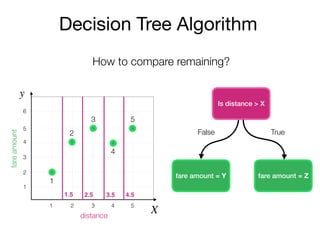
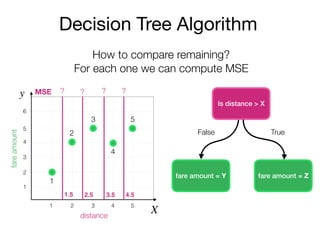
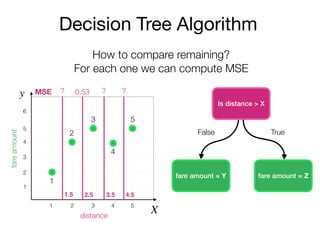
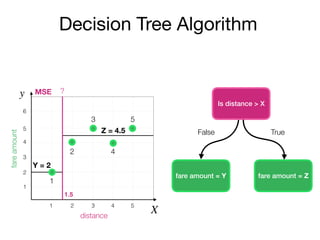
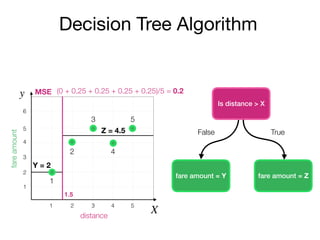
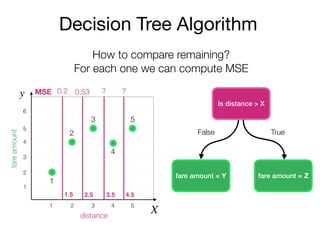
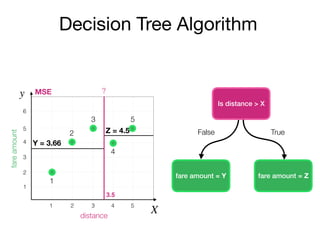
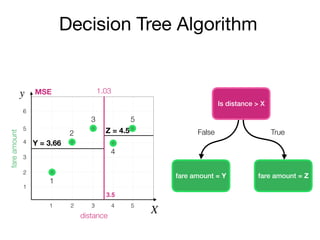
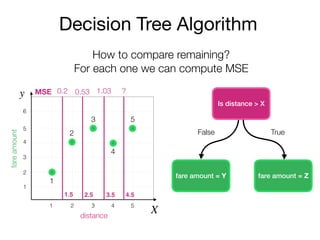
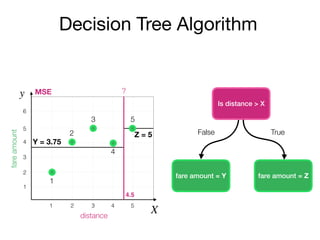
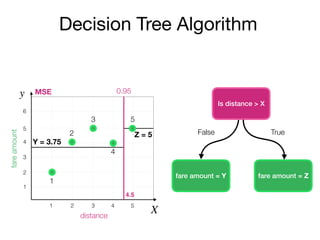
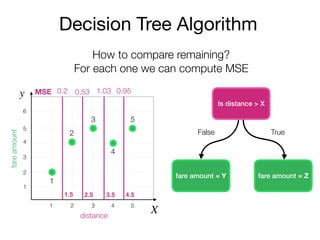
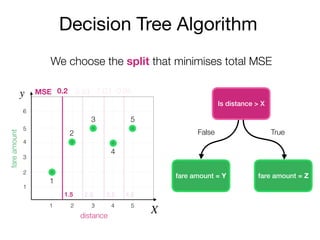
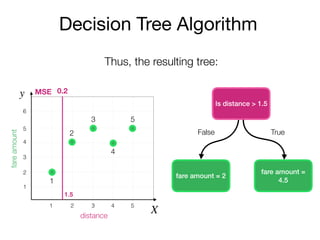
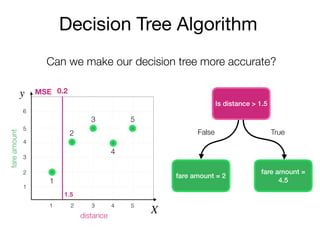
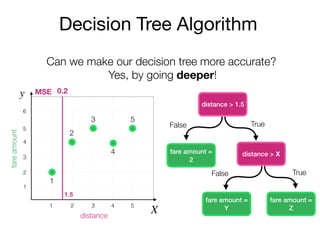
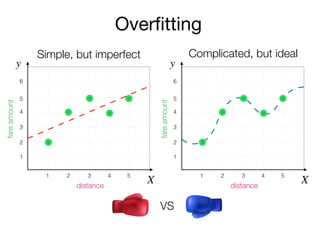
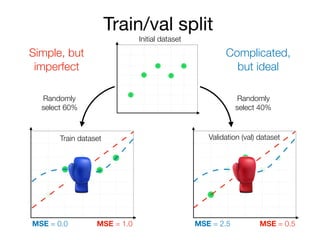
The document outlines a lecture on machine learning focused on predicting New York City taxi fares using linear regression and decision trees. It discusses the importance of independent and dependent variables and the minimization of errors using methods like least squares. Additionally, it explains the functioning of decision tree algorithms and how they can be applied to regression problems in predicting fare amounts based on distance.

1. INTRO TO MACHINE LEARNING
150
MIN
5.0
DMYTRO FISHMAN
UNIVERSITY OF TARTU
INSTITUTE OF COMPUTER SCIENCE

2. New York City Taxi
Fare Prediction
https://www.kaggle.com/c/new-york-city-taxi-fare-prediction

3. x
y
-0.8
0.2
-0.6
-0.4
-0.2
0.0
0.4
0.6
-0.75 -0.50 -0.25 0.00 0.25 0.50 0.75 1.00
type in your browser:
tinyurl.com/yxb5k5jl
(save a copy to your drive)

4. The following slides are inspired by
“An Introduction to Linear Regression Analysis” video
https://youtu.be/zPG4NjIkCjc

5. y
X
independent variable
dependentvariable
Linear Regression

6. y
X
independent variable
dependentvariable
Linear Regression
How the change in independent variable
influences dependent variable?

7. y
X
independent variable
dependentvariable
Positive relationship
Linear Regression

8. y
X
independent variable
dependentvariable
Negative relationship
Linear Regression

9. y
X
independent variable
dependentvariable
Linear Regression
In order to build a linear regression
we need observations

10. y
X
independent variable
dependentvariable
In order to build a linear regression
we need observations
Linear Regression

11. y
X
independent variable
dependentvariable
Linear Regression

12. y
X
independent variable
dependentvariable We want to find a line such that …
Linear Regression

13. y
X
independent variable
dependentvariable We want to find a line such that …
… it minimises the sum of errors
Linear Regression

14. y
X
independent variable
dependentvariable
actual
estimated
error
We want to find a line such that …
… it minimises the sum of errors
Linear Regression

15. y
X
independent variable
dependentvariable
arg min =
n
∑
i=1
( − )2yi ̂yi
Regression Line
Least squares method
We want to find a line such that …
… it minimises the sum of errors
Linear Regression

16. y
X
independent variable
dependentvariable
Linear Regression

17. y
X
fareamount
distance
Linear Regression

18. y
X
fareamount
̂y xw0 w1+=
distance
Linear Regression

19. y
X
fareamount
xw0 w1+=
arg min
,
=
n
∑
i=1
( − )2yi ̂yi
w0 w1
distance
̂y
Linear Regression
minimises the sum of errors with respect to w0 and w1w0 w1

20. y
X
fareamount
Linear Regression (example)
distance
2
3
4
5
6
1
1 2 3 4 5
x y x - x̄ y - ȳ (x - x̄ )2 (x - x̄ )(y - ȳ)
1 2 -2 -2 4 4
2 4 -1 0 1 0
3 5 0 1 0 0
4 4 1 0 1 0
5 5 2 1 4 2
x̄ = 3 ȳ = 4 10 6
xw0 w1+=̂y
w1
3w0 .6+=4 *
w0 = 2.2
2.2
=
∑ (x − x)(y − y)
∑ (x − x)2
=
6
10
= .6

21. =
∑ (x − x)(y − y)
∑ (x − x)2
=
6
10
= .6
y
X
fareamount
Linear Regression (example)
distance
2
3
4
5
6
1
1 2 3 4 5
x y x - x̄ y - ȳ (x - x̄ )2 (x - x̄ )(y - ȳ)
1 2 -2 -2 4 4
2 4 -1 0 1 0
3 5 0 1 0 0
4 4 1 0 1 0
5 5 2 1 4 2
x̄ = 3 ȳ = 4 10 6
xw0 w1+=̂y
w1
3w0 .6+=4 *
w0 = 2.2
2.2
Let’s return to our Colabs

22. Decision Tree Algorithm
By asking a simple question about value of independent
variable it tries to predict a value of dependent variable

23. Decision Tree Algorithm
By asking a simple question about value of independent
variable it tries to predict a value of dependent variable
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5

24. Decision Tree Algorithm
By asking a simple question about value of independent
variable it tries to predict a value of dependent variable
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5

25. Decision Tree Algorithm
By asking a simple question about value of independent
variable it tries to predict a value of dependent variable
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y
False

26. Decision Tree Algorithm
By asking a simple question about value of independent
variable it tries to predict a value of dependent variable
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True

27. Decision Tree Algorithm
By asking a simple question about value of independent
variable it tries to predict a value of dependent variable
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
Root node

28. Decision Tree Algorithm
By asking a simple question about value of independent
variable it tries to predict a value of dependent variable
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
Root node
Left child Right child

29. Decision Tree Algorithm
By asking a simple question about value of independent
variable it tries to predict a value of dependent variable
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
Root node
Left child Right child
Leafs

30. Decision Tree Algorithm
By asking a simple question about value of independent
variable it tries to predict a value of dependent variable
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True

31. Decision Tree Algorithm
Here, X may correspond to any vertical line.
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
For example if X = 2.5:
2.5

32. Decision Tree Algorithm
Here, X may correspond to any vertical line.
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
For example if X = 2.5:
2.5
What are most reasonable values
for Y and Z?

33. Decision Tree Algorithm
Here, X may correspond to any vertical line.
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
For example if X = 2.5:
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?

34. Decision Tree Algorithm
What would be MSE if Y = 4 and Z = 5?
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 4 fare amount = 5
False True
For example if X = 2.5:
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 4
Z = 5

35. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 4 fare amount = 5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 4
Z = 5
yi ̂yiMSE =
1
n
n
∑
i=1
( − )2

36. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 4 fare amount = 5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 4
Z = 5
yi ̂yiMSE =
1
n
n
∑
i=1
( − )2
real value
predicted value

37. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 4 fare amount = 5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 4
Z = 5
MSE =
1
n
n
∑
i=1
( − )2
=
(y1 − ̂y1)2
+ (y2 − ̂y2)2
+ (y3 − ̂y3)2
+ (y4 − ̂y4)2
+ (y5 − ̂y5)2
5
yi ̂yi
1
2
3
4
5

38. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 4 fare amount = 5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 4
Z = 5
MSE =
1
n
n
∑
i=1
( − )2
=
(y1 − ̂y1)2
+ (y2 − ̂y2)2
+ (y3 − ̂y3)2
+ (y4 − ̂y4)2
+ (y5 − ̂y5)2
5
yi ̂yi
1
2
3
4
5

39. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 4 fare amount = 5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 4
Z = 5
MSE =
1
n
n
∑
i=1
( − )2
=
(2)2
+ (0)2
+ (0)2
+ (1)2
+ (0)2
5
yi ̂yi
1
2
3
4
5

40. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 4 fare amount = 5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 4
Z = 5
MSE =
1
n
n
∑
i=1
( − )2
=
4 + 0 + 0 + 1 + 0
5
yi ̂yi
1
2
3
4
5

41. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 4 fare amount = 5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 4
Z = 5
MSE =
1
n
n
∑
i=1
( − )2
=
5
5
yi ̂yi
1
2
3
4
5

42. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 4 fare amount = 5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 4
Z = 5
MSE =
1
n
n
∑
i=1
( − )2
= 1yi ̂yi
1
2
3
4
5

43. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 4 fare amount = 5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 4
Z = 5
MSE =
1
n
n
∑
i=1
( − )2
= 1yi ̂yi
1
2
3
4
5
so, if X = 2.5, Y = 4 and Z = 5, MSE is 1

44. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 4 fare amount = 5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 4
Z = 5
MSE =
1
n
n
∑
i=1
( − )2
= 1yi ̂yi
1
2
3
4
5
Can we find better Y and Z?
so, if X = 2.5, Y = 4 and Z = 5, MSE is 1

45. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 3 fare amount = 5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 3
Z = 5
1
2
3
4
5
MSE =
1
n
n
∑
i=1
( − )2
=
(y1 − ̂y1)2
+ (y2 − ̂y2)2
+ (y3 − ̂y3)2
+ (y4 − ̂y4)2
+ (y5 − ̂y5)2
5
yi ̂yi

46. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 3 fare amount = 5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 3
Z = 5
1
2
3
4
5
MSE =
1
n
n
∑
i=1
( − )2
=
(2 − 3)2
+ (4 − 3)2
+ (5 − 5)2
+ (4 − 5)2
+ (5 − 5)2
5
yi ̂yi

47. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 3 fare amount = 5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 3
Z = 5
1
2
3
4
5
MSE =
1
n
n
∑
i=1
( − )2
=
1 + 1 + 0 + 1 + 0
5
yi ̂yi

48. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 3 fare amount = 5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 3
Z = 5
1
2
3
4
5
MSE =
1
n
n
∑
i=1
( − )2
=
3
5
= 0.6yi ̂yi

49. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 3 fare amount = 5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 3
Z = 5
1
2
3
4
5
MSE =
1
n
n
∑
i=1
( − )2
=
3
5
= 0.6yi ̂yi
so, if X = 2.5, Y = 3 and Z = 5,
MSE is 0.6

50. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 3
fare amount =
4.5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 3
Z = 4.66
1
2
3
4
5
MSE =
1
n
n
∑
i=1
( − )2
=
(2 − 3)2
+ (4 − 3)2
+ (5 − 4.66)2
+ (4 − 4.66)2
+ (5 − 4.66)2
5
yi ̂yi

51. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 3
fare amount =
4.5
False True
2.5
What are most reasonable values for Y
and Z (that minimise total MSE)?
Y = 3
1
2
3
4
5
MSE =
1
n
n
∑
i=1
( − )2
=
1 + 1 + 0.12 + 0.43 + 0.12
5
yi ̂yi
Z = 4.66

52. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 3
fare amount =
4.5
False True
2.5
Y = 3
1
2
3
4
5
MSE =
1
n
n
∑
i=1
( − )2
=
2.67
5
= 0.53yi ̂yi so, if Y = 3 and Z = 4.5,
MSE is smallest
Are we happy?
Z = 4.66

53. Decision Tree Algorithm
Is distance > 2.5
fare amount = 3
fare amount =
4.5
False True
Hold on, how did we choose this split on the first place?
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
2.5
1
2
3
4
5

54. Decision Tree Algorithm
Is distance > 2.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 3
fare amount =
4.5
False True
2.5
1
2
3
4
5
Hold on, how did we choose this split on the first place?
Maybe there are better options?

55. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
What are the possible split options in this case?

56. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
What are the possible split options in this case?
0.5 1.5 2.5 3.5 4.5 5.5

57. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
Are these meaningful?
0.5 5.5

58. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
How to compare remaining?
1.5 2.5 3.5 4.5

59. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
How to compare remaining?
For each one we can compute MSE
?? ? ?MSE
1.5 2.5 3.5 4.5

60. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
How to compare remaining?
For each one we can compute MSE
0.53? ? ?
1.5 2.5 3.5 4.5
MSE

61. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
?
Y = 2
Z = 4.5
1.5
MSE

62. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
(0 + 0.25 + 0.25 + 0.25 + 0.25)/5 = 0.2
Y = 2
Z = 4.5
1.5
MSE

63. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
How to compare remaining?
For each one we can compute MSE
0.2 ? ?
1.5 2.5 3.5 4.5
MSE 0.53

64. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
?
3.5
MSE
Y = 3.66
Z = 4.5

65. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
1.03
3.5
MSE
Y = 3.66
Z = 4.5

66. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
How to compare remaining?
For each one we can compute MSE
0.2 1.03 ?
1.5 2.5 3.5 4.5
MSE 0.53

67. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
?
4.5
MSE
Y = 3.75
Z = 5

68. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
0.95
4.5
MSE
Y = 3.75
Z = 5

69. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
How to compare remaining?
For each one we can compute MSE
0.2 1.03 0.95
1.5 2.5 3.5 4.5
MSE 0.53

70. Decision Tree Algorithm
Is distance > X
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = Y fare amount = Z
False True
1
2
3
4
5
We choose the split that minimises total MSE
0.2 1.03 0.95
1.5 2.5 3.5 4.5
MSE 0.53

71. Decision Tree Algorithm
Is distance > 1.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 2
fare amount =
4.5
False True
1
2
3
4
5
Thus, the resulting tree:
0.2
1.5
MSE

72. Decision Tree Algorithm
Is distance > 1.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
fare amount = 2
fare amount =
4.5
False True
1
2
3
4
5
Can we make our decision tree more accurate?
0.2
1.5
MSE

73. Decision Tree Algorithm
distance > 1.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
False True
1
2
3
4
5
Can we make our decision tree more accurate?
0.2
1.5
MSE
Yes, by going deeper!
fare amount =
2
distance > X
fare amount =
Y
fare amount =
Z
False True

74. Decision Tree Algorithm
distance > 1.5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
False True
1
2
3
4
5
Can we make our decision tree more accurate?
0.2
1.5
MSE
Yes, by going deeper!
fare amount =
2
distance > X
fare amount =
Y
fare amount =
Z
False True
Let’s return to our Colabs

75. Overfitting
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
y
X
fareamount
distance
2
3
4
5
6
1
1 2 3 4 5
Simple, but imperfect Complicated, but ideal
VS

76. Train/val split
Initial dataset
MSE = 1.0
Train dataset
Randomly
select 60%
MSE = 0.0
Simple, but
imperfect
Complicated,
but ideal
Validation (val) dataset
Randomly
select 40%
MSE = 2.5 MSE = 0.5

77. POINTS

78. POINTS
1. MACHINE LEARNING
MODEL IS NOT MAGIC
2. YOU CAN SAVE AND
LOAD ML MODELS
3. EVALUATING MODEL
PERFORMANCE IS
IMPORTANT
4. YOU MAY NEED TO
RETRAIN YOUR
MODELS

79. THANK YOU