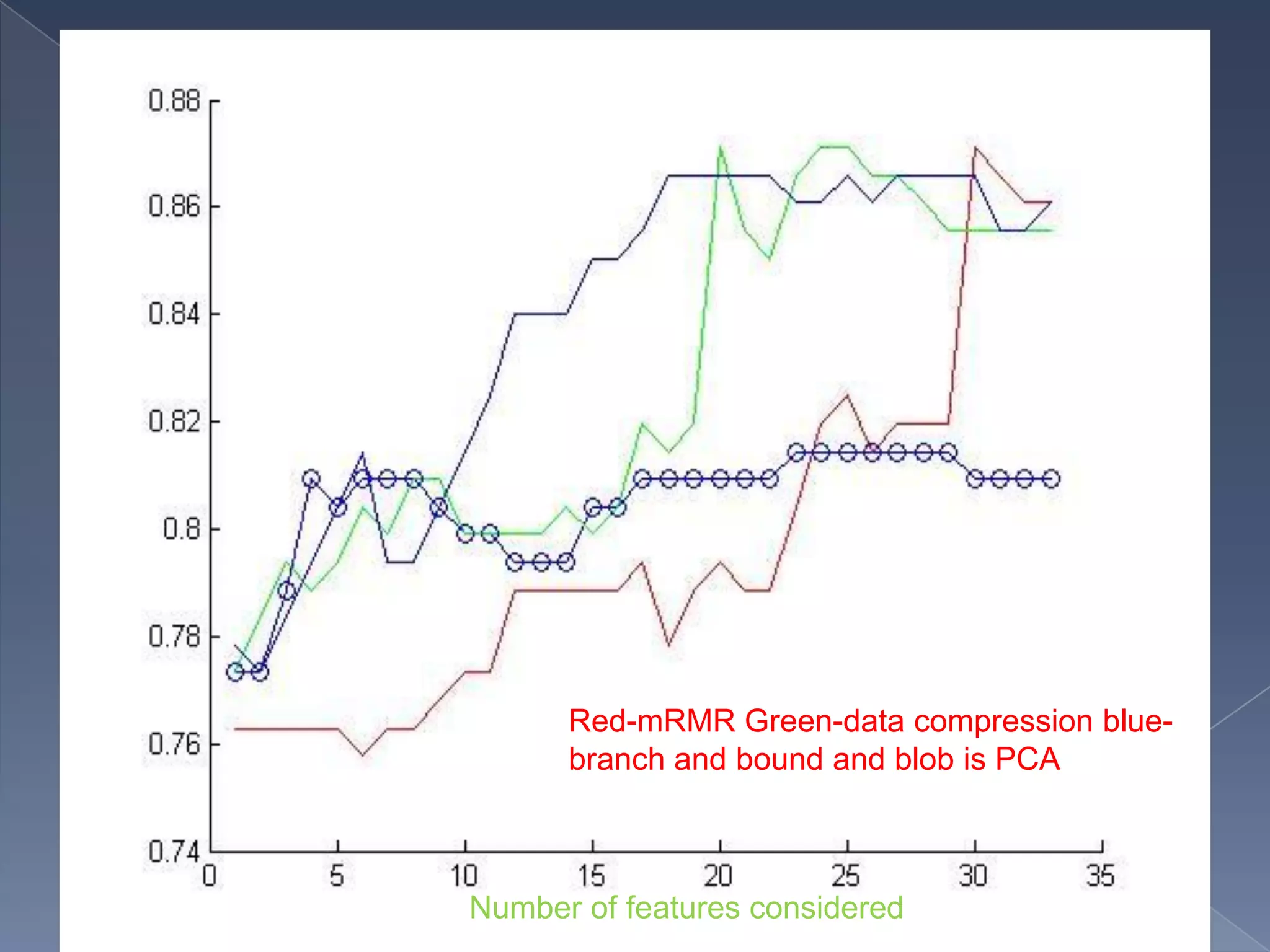
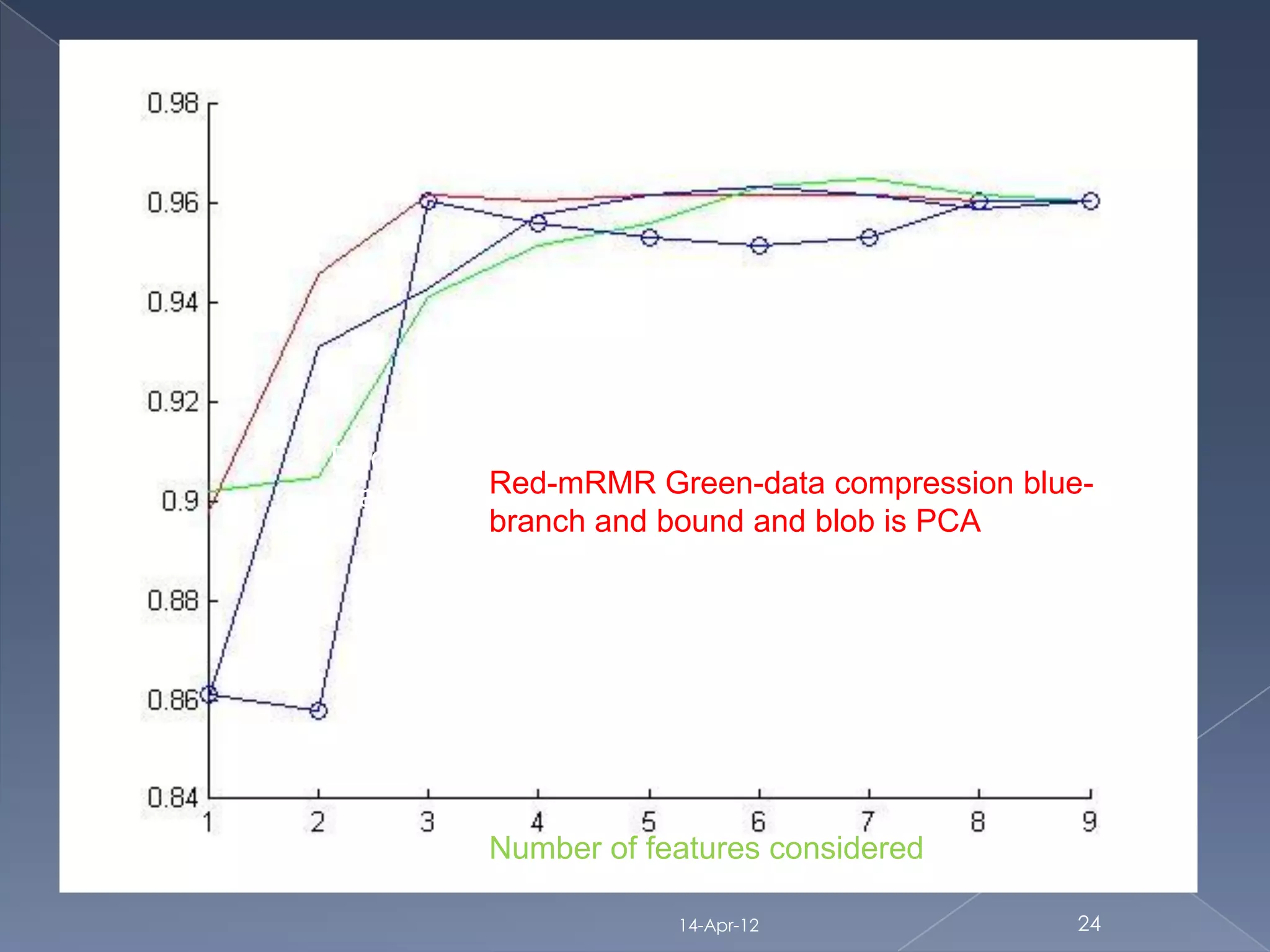
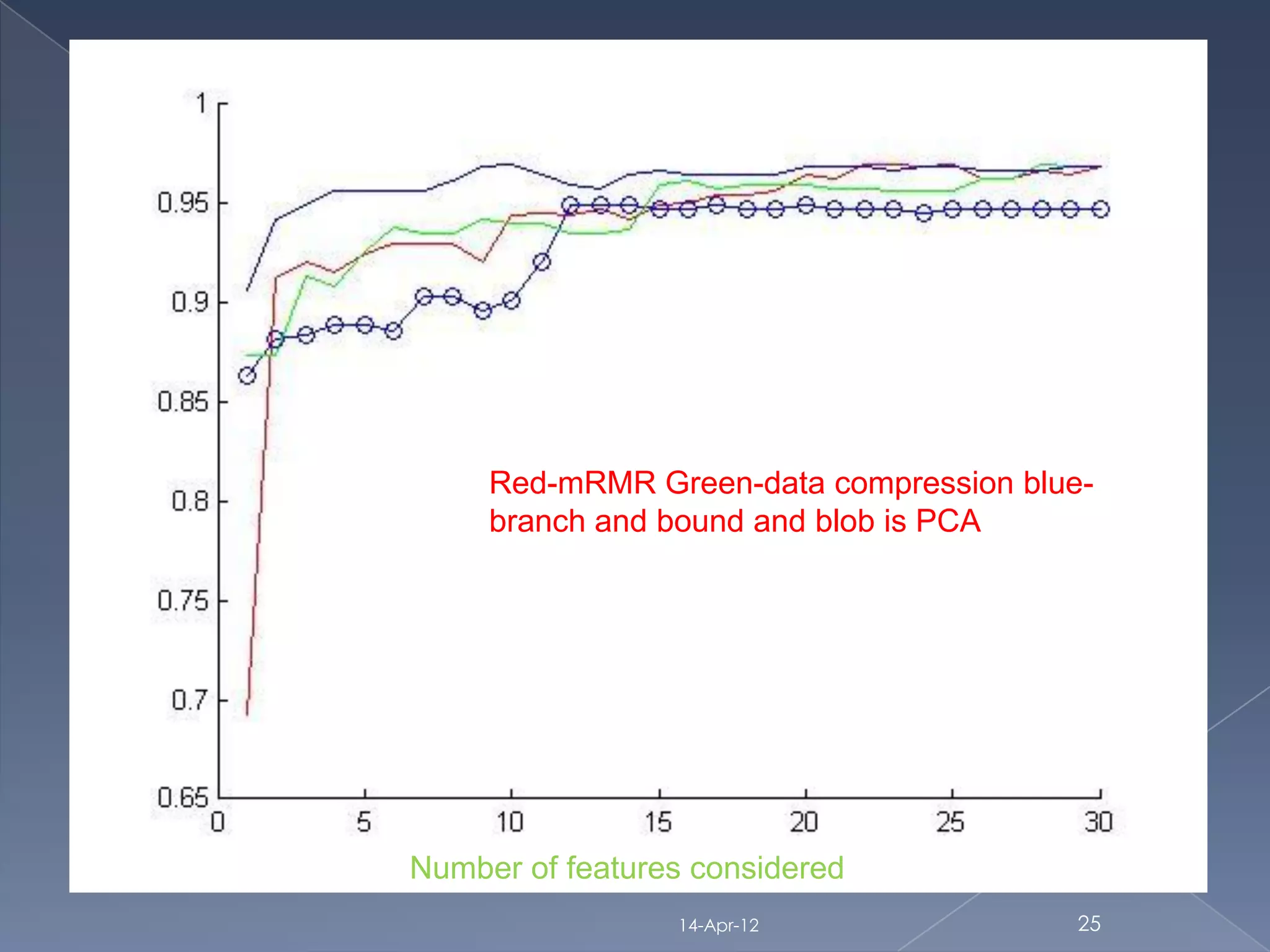
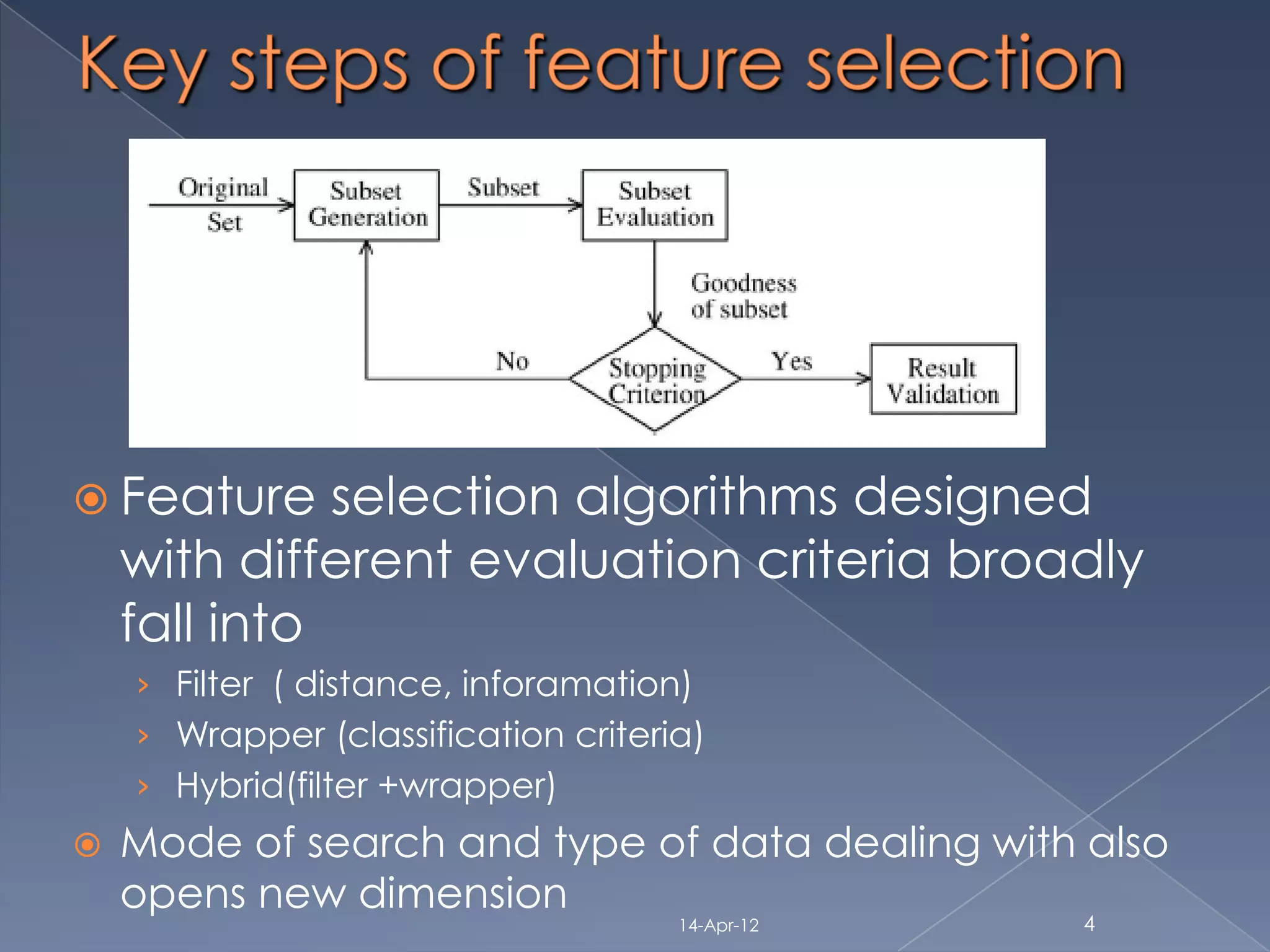
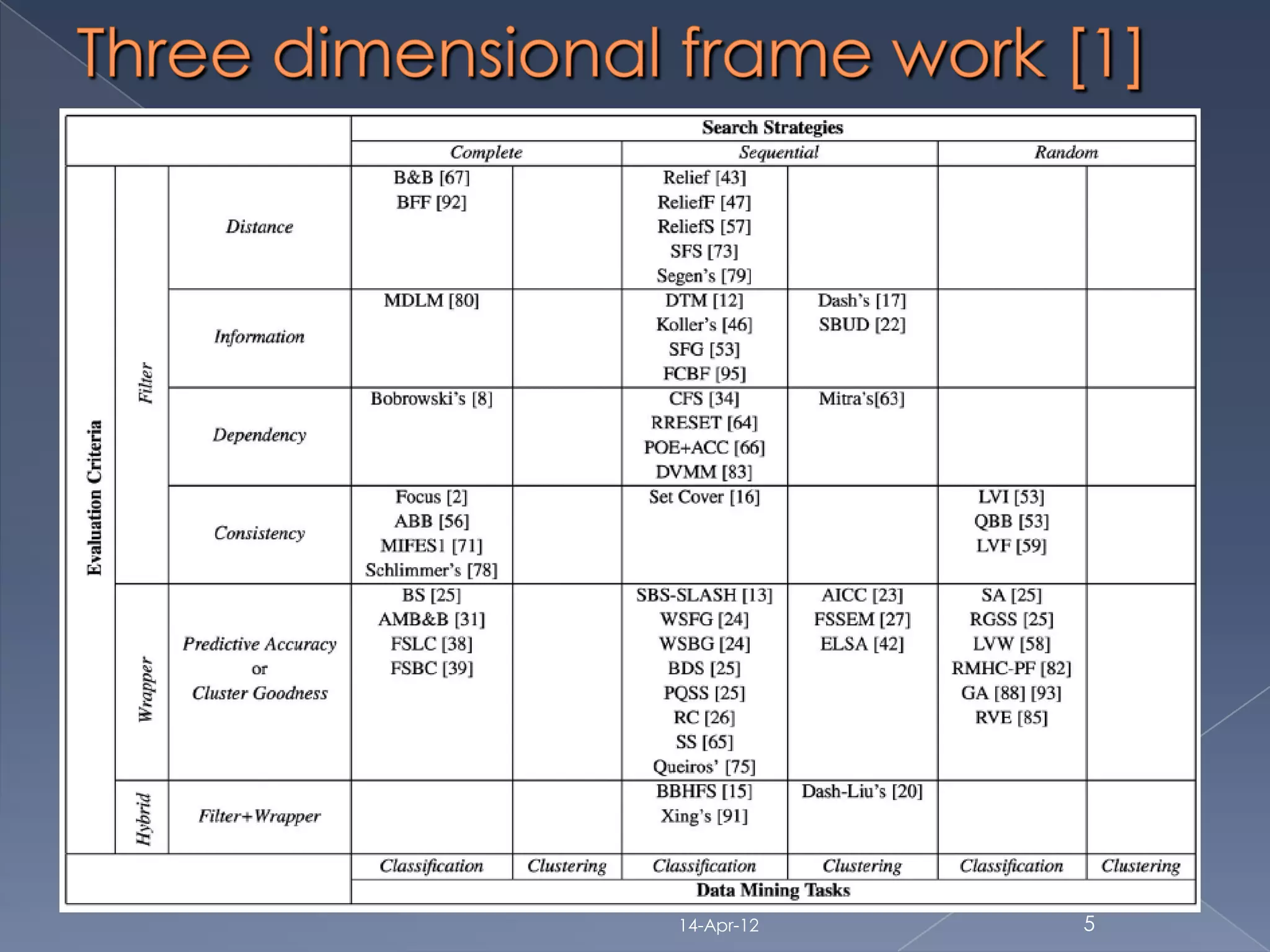
The document discusses dimensionality reduction techniques for reducing high-dimensional data to fewer dimensions. It categorizes dimensionality reduction into feature extraction and feature selection. Feature extraction transforms features to generate new ones, while feature selection selects the best original features. The document then discusses several feature selection algorithms from different categories (filter, wrapper, hybrid) and evaluates their performance on cancer datasets. It finds that linear support vector machines using mRMR feature selection provided the best results.

1. K.S .Phani krishna
11MM91R05
1
14-Apr-12

2.  Dimensionality Reduction(DR)
› Reduction of data with „D‟ dimensions to „d‟ dimensions
 Based
on resulting features DR is
categorized to
› DR by Feature extraction
› DR by Feature selection
 Feature extraction
› Linear/non-linear transformation of current features to
generate new features
 Feature selection
› No transformation but to select the best ones from original set
of features
› Reduction of computation and discussion with domain experts
14-Apr-12 2

3.  In present days for accurate analysis
data from different modules are taken
and fused
 This rapidly increases the features
dimensionality
 Dimensionality reduction is required with
out changing the toplogy of features for
future discussions with domain
experts(doctors)

14-Apr-12 3

4.  Feature selection algorithms designed
with different evaluation criteria broadly
fall into
› Filter ( distance, inforamation)
› Wrapper (classification criteria)
› Hybrid(filter +wrapper)
 Mode of search and type of data dealing with also
opens new dimension
14-Apr-12 4

5. 14-Apr-12 5

6. algorithms from various categories are considered for
understandability of various domains
 Unsupervised feature selection using
feature similarity [P.Mitra 2002](covers
filter: dependancy search: sequential and clustering )
 Feature selection based on mutual
information [H.Peng 2005](covers wrapper: {filter:
information+ classifier bayesian}search: sequential and classification)
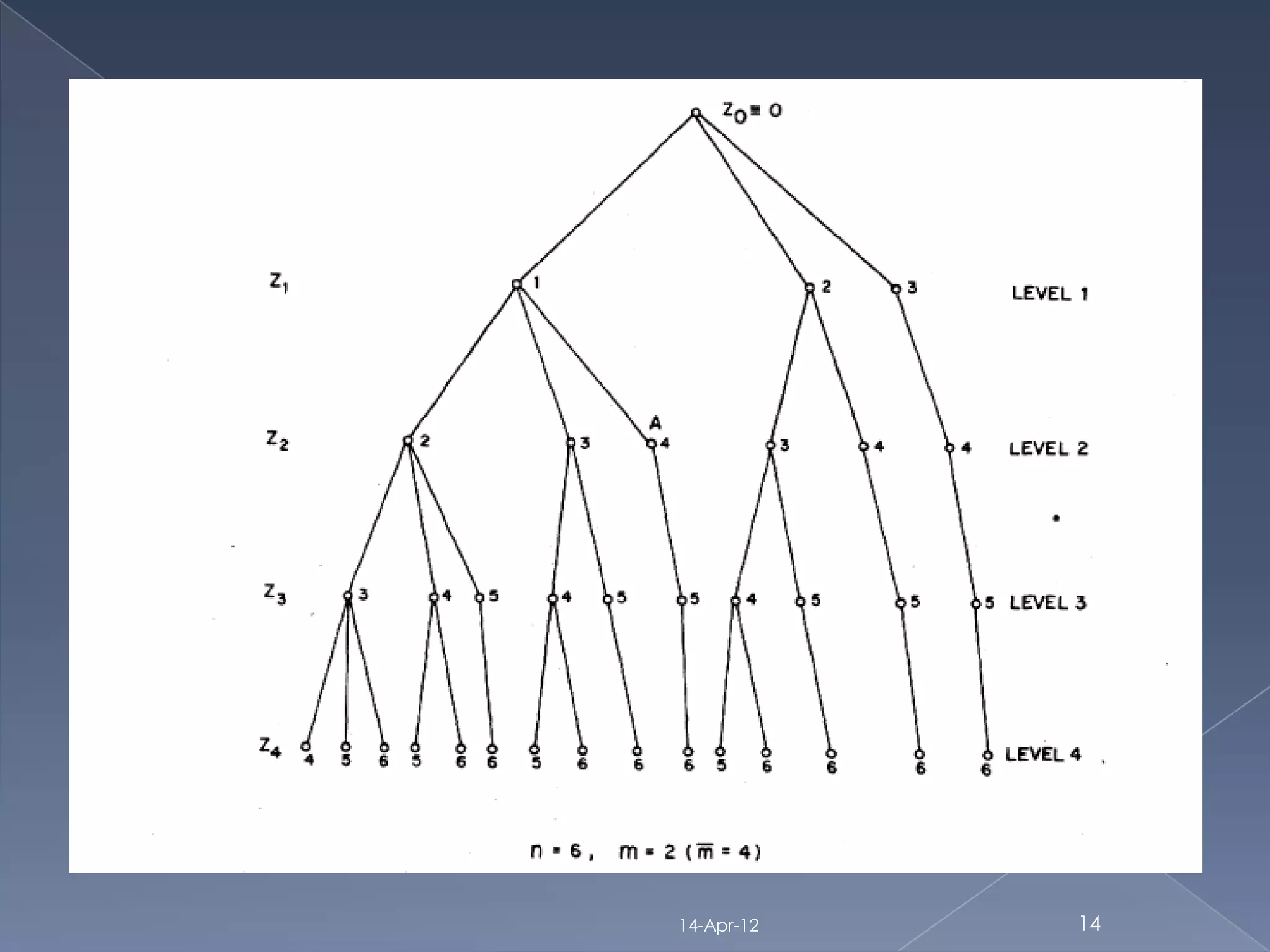
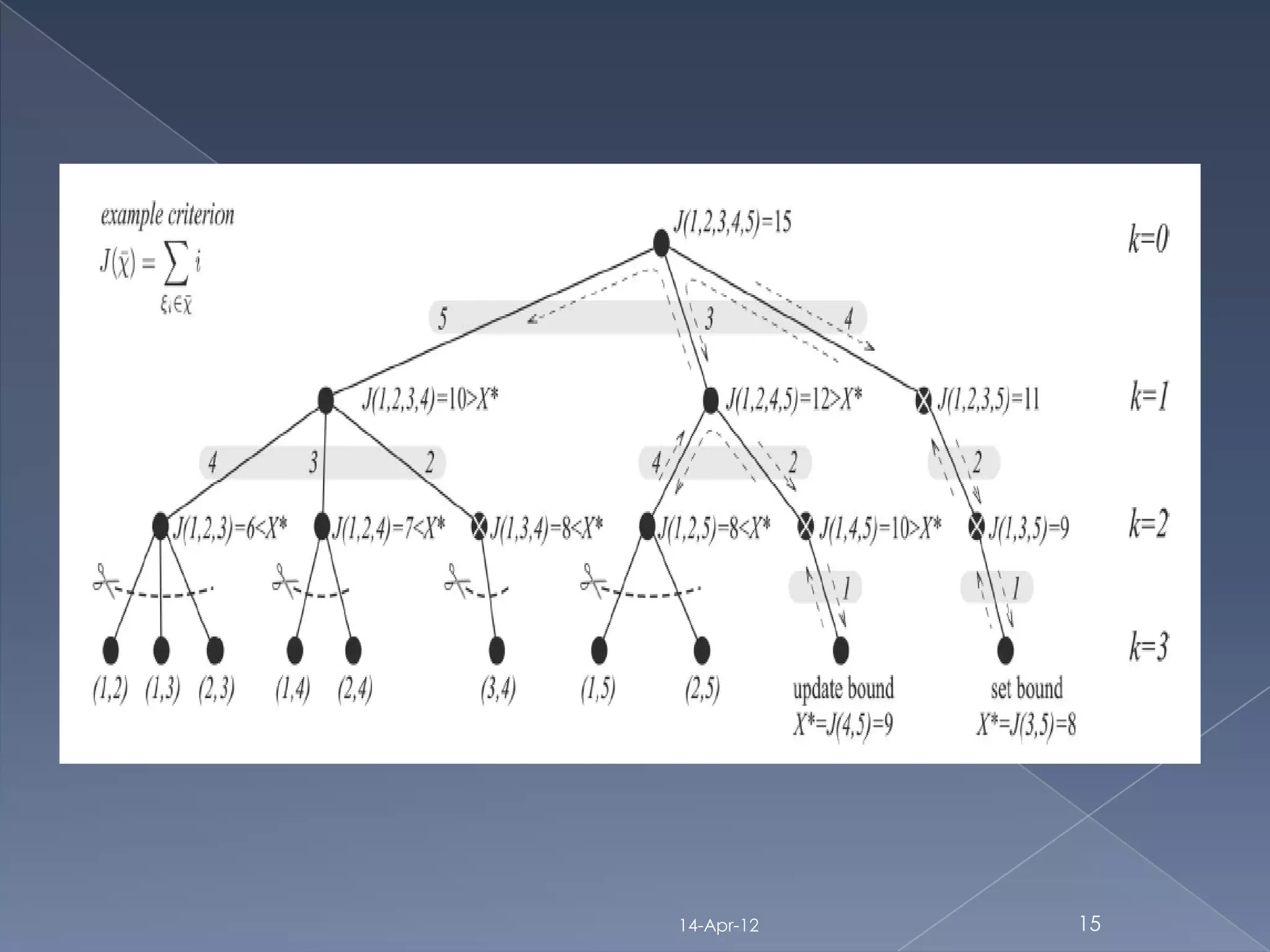
A branch and bound algorithm for
feature subset selection[P.M.Narendra
1977] (covers filter: distance search: complete and classification)
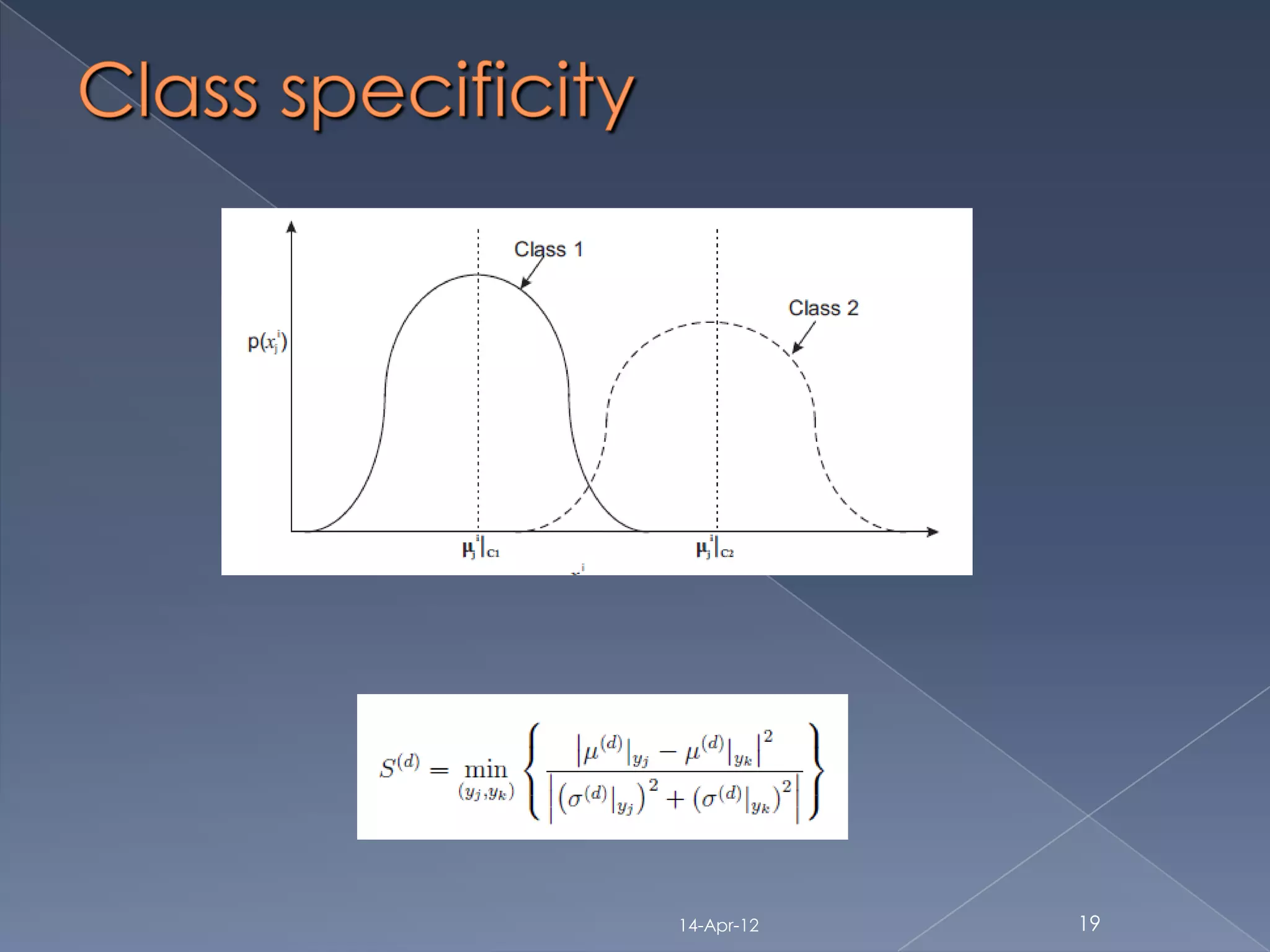
 Feature usability Index [D.Sheet 2010]
14-Apr-12 6

7.  Sequential search using Dependency
criteria on a unlabelled data
 removal of redundant features
› Redundant feature is this context is a “feature which caries
little or no additional information beyond that subsumed
by remaining features”
 Introduced a similarity measure
› Minimization of information loss in process of feature
elimination
› Zero when features are linearly dependent
› Symmetry
› Sensitivity to scaling
› Invariance to rotation
› Can compute in less time O(D2)
14-Apr-12 7

8. Maximal information compression
Index(MICI)
MICI is eigen value for the direction normal to
prinicipal component direction of feature pair(X,Y)
Maximum information is achieved if multivariate data
is projected along principle component direction
14-Apr-12 8

9. MICI(X,Y)=MIN(eig(cov(X,Y))))
= 0.5*(var(X)+var(Y)-4*sqrt((var(X)+var(Y))^2-4*var(X)*var(Y)*(1-
corr(X,Y)^2)))
 Selection method:-
› Partitioning of original data into
homogeneous clusters based on k-NN
principle using MICI
› From each set most compact features are
selected and remaining k candidates are
discarded
› Set threshold=min(MICI in first iteration)
› For successive iteration if MICI > threshold
K=k-1;
14-Apr-12 9

10.  Sequential search using Dependency
criteria on a labelled data
 Generally known as Max-relevance and
Min-redundancy
› Sprouted out from maximal dependacy
 For the first order incremental search mRMR is
equalent to max dependancy
 selection of optimalfeatures
› optimal feature is this context is a “feature which has more
information regarding(Relevance) target class and least
correlated (Redundancy) to other features ”
14-Apr-12 11

11. Using mRMR criteria select n sequential features from the input X.
14-Apr-12 12

12.  complete search using Distance criteria
on a labelled data
 Sequential search
› given D feature, need d fetures
› No. of subsets toevaluate= D!/(d!*(D-d)!)
 Evaluating
criteria „J‟should satisfy
monotonicity
14-Apr-12 13

13. 14-Apr-12 14

14. 14-Apr-12 15

15.  Ranking of individual feature based on
› Homogeneity
› Class specificity
› Error in decision making
Homogeneity:-
one oulier scatter ratio
14-Apr-12 18

16. 14-Apr-12 19

17. 14-Apr-12 20

18.  UCI machine learning repository
 3 data sets on breast cancer
 Data1:- 194 samples 33 features
 Data2:- 683 samples 9 features
 Data3:- 569 samples 30 features
14-Apr-12 21

19.  Acquired data is k-fold processed
 Classifiers used are lin-SVM, kmeans and
bayesian but linear SVM has given
presentable results
 Plotted the accuracy on y axis and
number os features selected on x axis
 In plots Red -mRMR Green-data
compression blue- branch and bound
and blbo is PCA
14-Apr-12 22

20. Red-mRMR Green-data compression blue-
branch and bound and blob is PCA
Number of features considered
14-Apr-12 23

21. Red-mRMR Green-data compression blue-
branch andRed-mRMRblbo is PCA compression blue-
bound and Green-data
branch and bound and blob is PCA
Number of features considered
14-Apr-12 24

22. Red-mRMR Green-data compression blue-
branch and bound and blob is PCA
Number of features considered
14-Apr-12 25

23. Narendra, P. and Fukunaga, K. (1977). A branch and bound algorithm for
feature subset selection, Computers, IEEE Transactions on C- 26(9): 917–
922.
somel, (20ering10).efficient feature subset selection
p.mitra(2002).unsupervised feature selection using feature similarity
Huan.l (2005) towards integrating feature selection algorithm for classification
and clus
Debdoot sheet (2010); Feature usability index and optimal feature subset
selection, International journal of computer applications
14-Apr-12 26