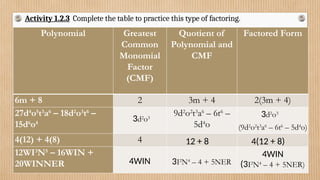
Factoring involves finding the factors of an expression, reversing the process of multiplication. Key techniques include identifying the greatest common factor (GCF), factoring by grouping, and using properties of polynomials. The document emphasizes step-by-step methods for factoring various polynomial expressions and distinguishing factorable from non-factorable polynomials.

1. Factoring

2. The process of finding the factors of an expression is called
factoring, which is the reverse process of multiplication.
Factoring the Greatest Common Monomial Factor
Factoring Quadratic Trinomials
Factoring the Difference of Two Squares and Sum or
Difference of Two Cubes
Factoring by Grouping

3. Factoring by Common Monomial Factor
Review: Find the GCF (Greatest Common Factor)
1. 4, 8, 12
GCF = 4
Listing Method
4
8
12
The highest number that divides exactly into two or more numbers.

4. Review: Find the GCF (Greatest Common Factor)
1. 4, 8, 12 GCF = 4
Factor Tree Method
4 8 12

5. Review: Find the GCF (Greatest Common Factor)
1. 4, 8, 12 GCF = 4
Synthetic Division
4 8 12

6. Factoring by Common Monomial Factor
Review: Find the GCF (Greatest Common Factor)
2. 3, 24, 12 = 3
3. 16, 12, 28

7. Factoring by Common Monomial Factor
Review: Find the GCF (Greatest Common Factor)
4. 30, 40, 50
5. 18, 36, 54
6. 33, 44, 121
7. 49, 21, 63
8. 22, 18, 84
9. 34, 72, 343

8. Factoring by Common Monomial Factor
Review: Find the GCF (Greatest Common Factor)
10. 12

9. Factoring by Common Monomial Factor
Review: Find the GCF (Greatest Common Factor)
11. 20

10. Factoring by Common Monomial Factor
The Distribution Property is used to factor out the GCF
of the terms in a polynomial and to write the polynomial
in factored form.
Recall that the Distributive Property states that
The expression is the factored form of is the common
factor of the terms.

11. Factoring by Common Monomial Factor
Factoring is the reverse of multiplication.
In factoring polynomials, we use the following steps:
1. Find the greatest common factor of the numerical coefficients.
Find the factor of 12x3
y5
– 20x5
y2
z
The GCF of 12 and 20 is 4.
2. Find the variable with the least exponent that appears in each term of
the polynomial. x and y are both common to all terms
3 is the smallest exponent for x 2 is the smallest exponent of y
thus, x3
y2
is the GCF of the variables.

12. Factoring by Common Monomial Factor
In factoring polynomials, we use the following steps:
3. The product of the greatest common factor in (1) and (2) is the GCF of the
polynomial.
Find the factor of 12x3
y5
– 20x5
y2
z
The GCF of 12 and 20 is 4 and x3
y2
is the GCF of the variables.
Hence, 4x3
y2
is the GCF of 12x3
y5
– 20x5
y2
z.

13. Factoring by Common Monomial Factor
In factoring polynomials, we use the following steps:
4. To completely factor the given polynomial, divide the polynomial by its
GCF, the resulting quotient is the other factor.
Find the factor of 12x3
y5
– 20x5
y2
z
12x3
y5
– 20x5
y2
z divided by 4x3
y2
4x3
y2
(3y3
– 5x2
z)

14. Factor each polynomial:
1. 9
1. 9
2. 5
= 3x (3x + 5)
= 5 (1 - 5)
3. 12y(x+y) + 32(x+y) = (x+y)(12y + 32)
4(3y + 8)
= 4(x+y) (3y + 8)

15. Polynomial Greatest
Common
Monomial
Factor
(CMF)
Quotient of
Polynomial and
CMF
Factored Form
6m + 8 2 3m + 4 2(3m + 4)
27d4
o5
t3
a6
– 18d2
o3
t6
–
15d6
o4
9d2
o2
t3
a6
– 6t6
–
5d4
o
4(12) + 4(8) 4
12WI3
N5
– 16WIN +
20WINNER
Activity 1.2.3 Complete the table to practice this type of factoring.
12 + 8 4(12 + 8)
4WIN 3I2
N4
– 4 + 5NER
4WIN
(3I2
N4
– 4 + 5NER)
3d2
o3 3d2
o3
(9d2
o2
t3
a6
– 6t6
– 5d4
o)

16. Question: Are all polynomials factorable?
No, if a polynomial is not factorable, then we classify it
as a prime or irreducible polynomial.

17. a
b
a
c
e
d

18. Factor each polynomial. Check your answer.
1.10m2
– m3
6. 9a2
+ 27a + 18
2.49pm2
– 7pm4
7. 13b2
– 11a2
b – 12 ab
3.42k2
– 7k5
8. 12x3
y – 6x2
y –
3xy
4.-27m4
+ 3m2
– 9mnk 9. 10r3
s2
+ 25r2
s2
– 15r2
s3
5.48k2
– 8k6
– 6 10. 8p6
– 40p4
+ 24p3
–

19. Factor each polynomial. Check your answer.
1.10m2
– m3
2.49pm2
– 7pm4
3.42k2
– 7k5
= m2
(10 –m)
= 7pm2
(7 - m2
)
= 7k2
(6 – k3
)

20. Factor each polynomial. Check your answer.
= 3m (-9m3
+ m – 3nk)
= 2(24k2
- 4k6
– 3)

21. Factor each polynomial. Check your answer.
= 9 (a2
+ 3a + 2)
= b(13b – 11a2
– 12a)

22. Factor each polynomial. Check your answer.
= 3xy (4x2
– 2x - 1)
= 5r2
s2 (2r+ 5 – 3s)
= 8p2 (p4
- 5p2
+3p - 2)