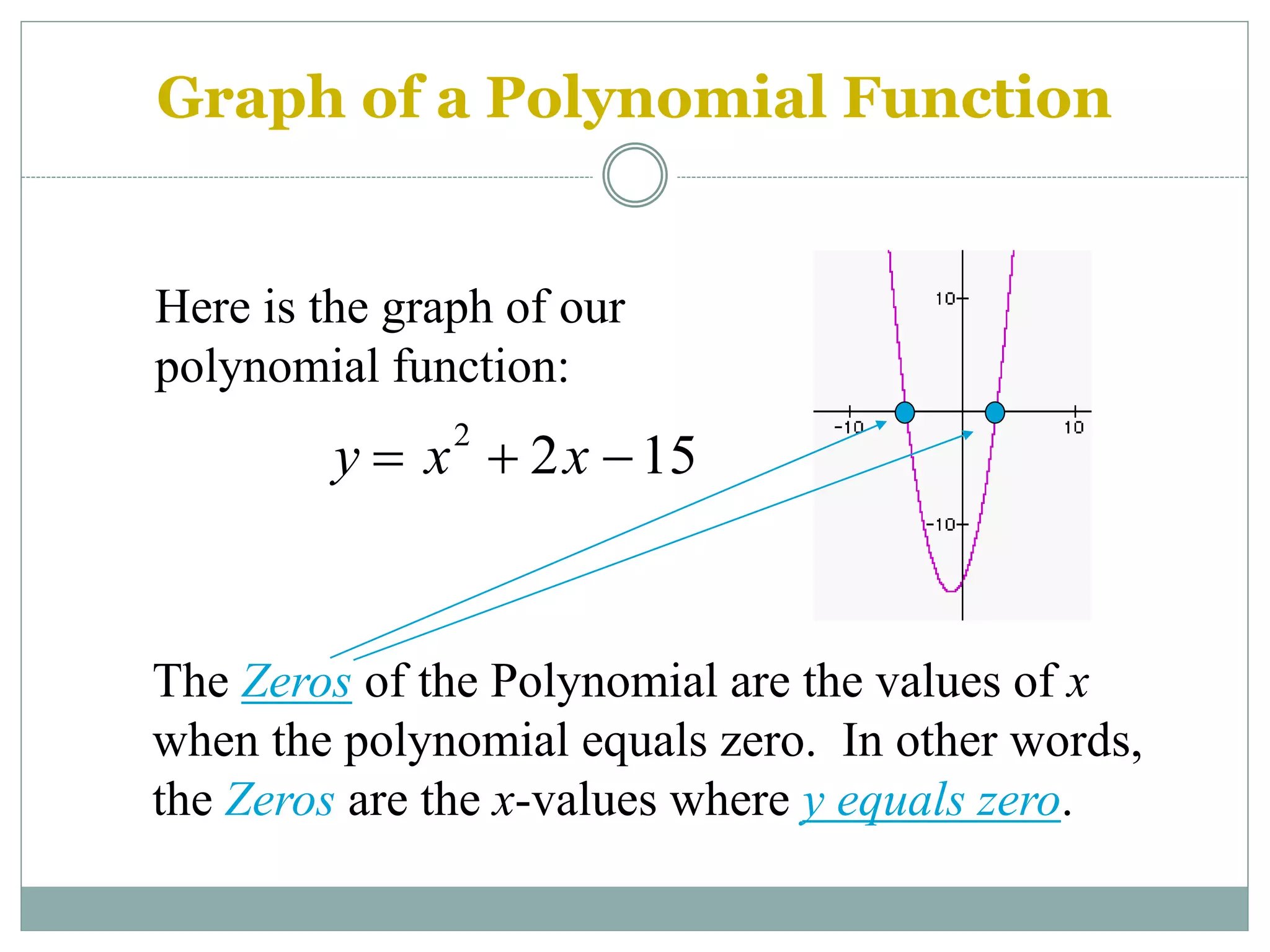
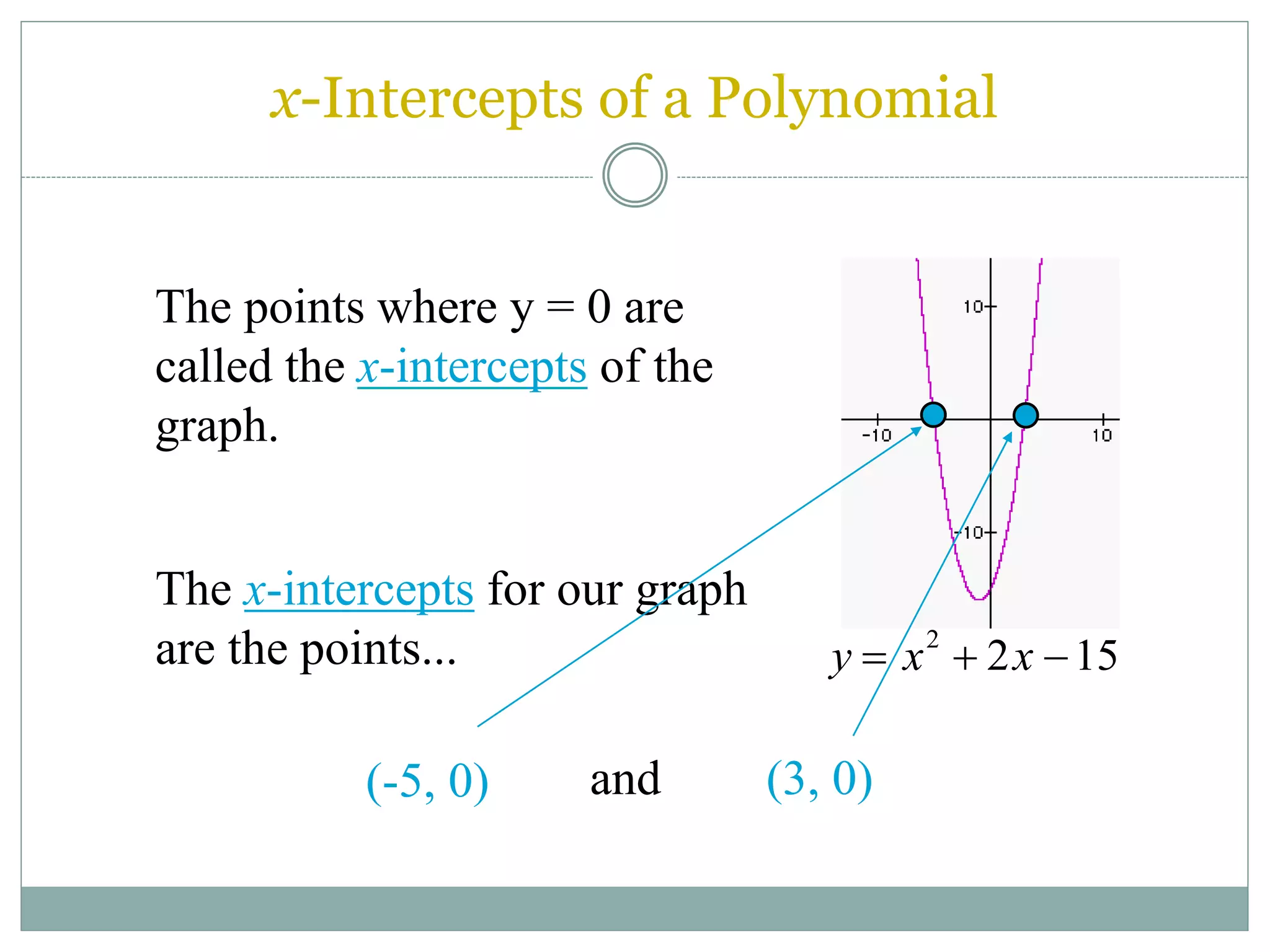
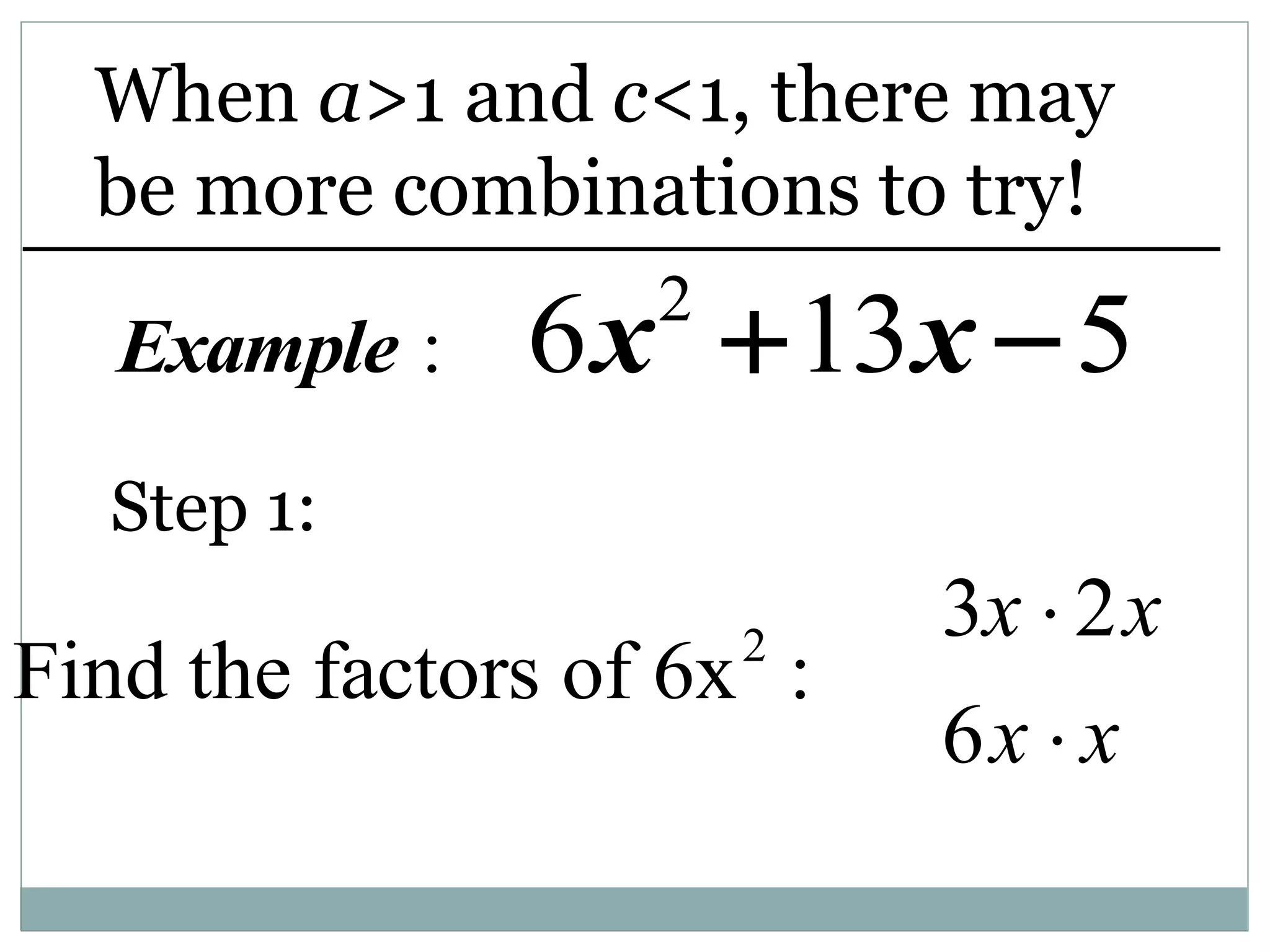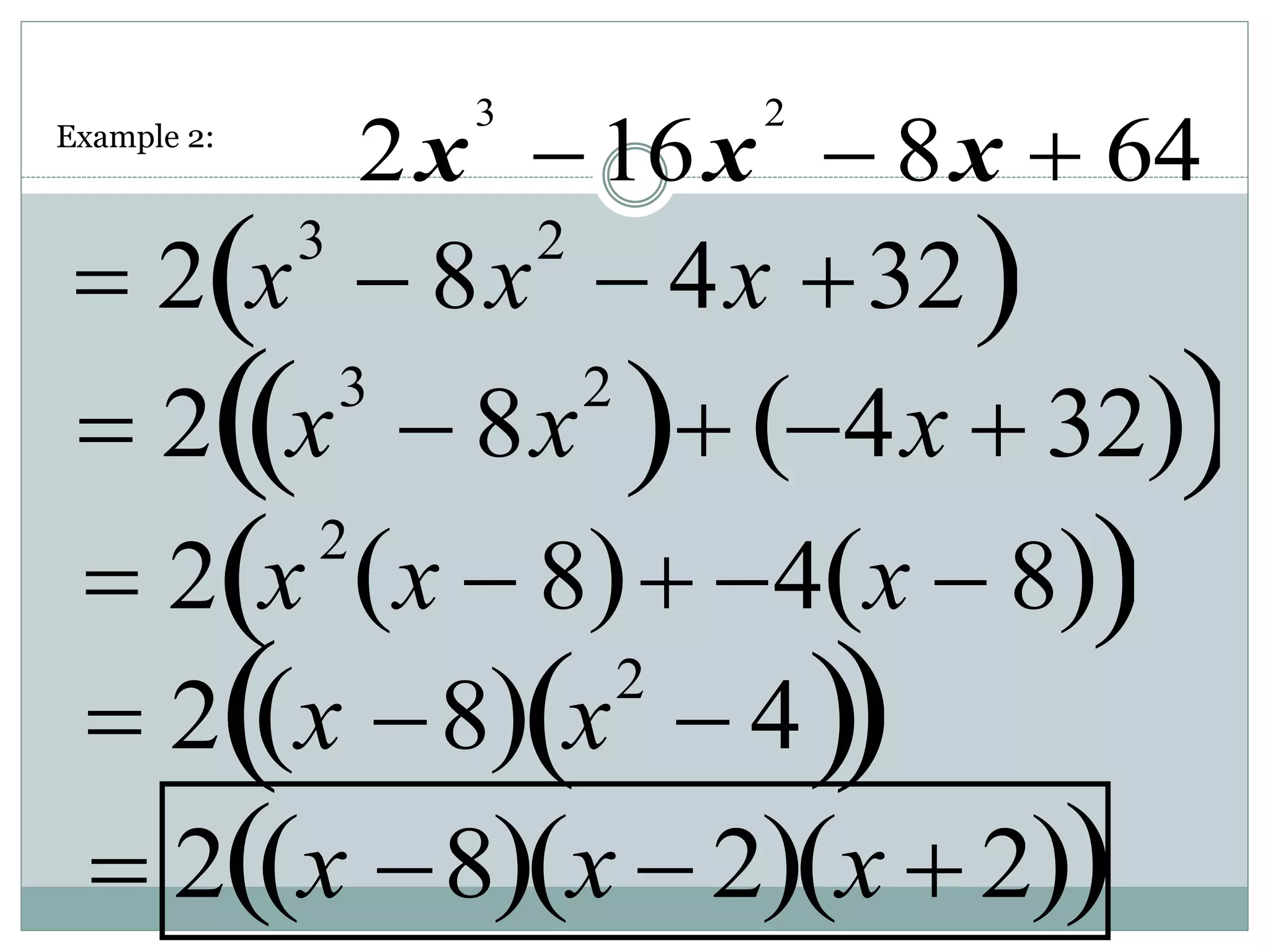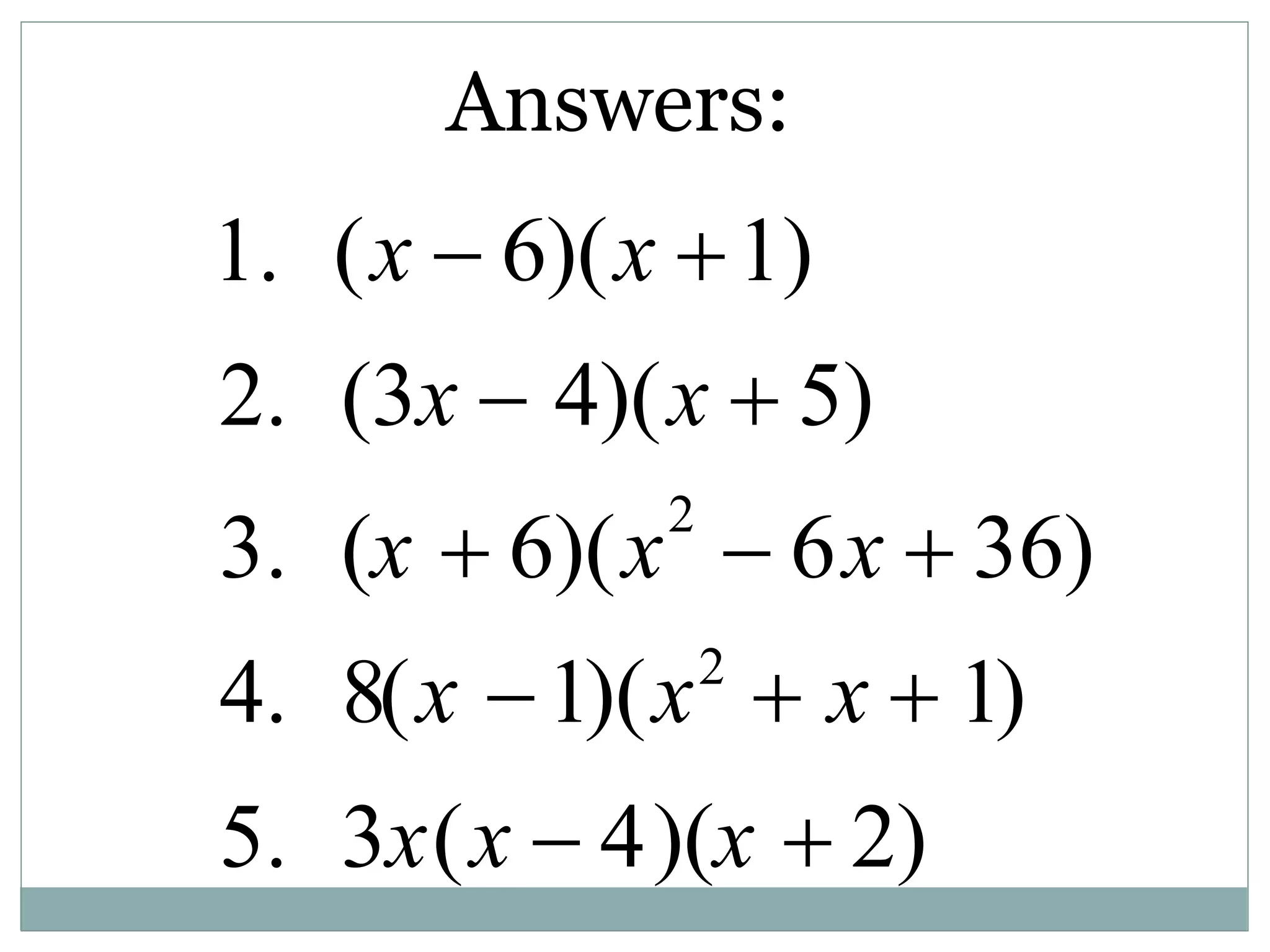The document discusses factoring polynomials and finding the roots of polynomial equations. It defines polynomials and polynomial equations. It then covers several methods for factoring polynomials, including factoring polynomials with a common monomial factor, factoring polynomials that are a difference of squares, factoring trinomials, and factoring polynomials by grouping. It also discusses using the factors to find the solutions or roots of a polynomial equation, which are also known as the zeros of a polynomial function.

1. Factoring and Finding Roots of
Polynomials

2. Polynomials
A Polynomial Expression can be a monomial or a
sum of monomials. The Polynomial Expressions
that we are discussing today are in terms of one
variable.
In a Polynomial Equation, two
polynomials are set equal to each other.

3. Factoring Polynomials
Terms are Factors of a Polynomial if, when they
are multiplied, they equal that polynomial:
2
2 15 ( 3)( 5)
x x x x
    
 (x - 3) and (x + 5) are Factors
of the polynomial
2
2 15
x x
 

4. Since Factors are a Product...
…and the only way a product can equal zero
is if one or more of the factors are zero…
…then the only way the polynomial can
equal zero is if one or more of the factors are
zero.

5. Solving a Polynomial Equation
The only way that x2 +2x - 15 can = 0 is if x = -5 or x = 3
Rearrange the terms to have zero on one side:
2 2
2 15 2 15 0
x x x x
     
Factor:
( 5)( 3) 0
x x
  
Set each factor equal to zero and solve:
( 5) 0 and ( 3) 0
5 3
x x
x x
   
  

6. Solutions/Roots a Polynomial
Setting the Factors of a Polynomial
Expression equal to zero gives the
Solutions to the Equation when the
polynomial expression equals zero.
Another name for the Solutions of a
Polynomial is the Roots of a
Polynomial !

7. Zeros of a Polynomial Function
A Polynomial Function is usually written in
function notation or in terms of x and y.
f (x)  x2
 2x 15 or y  x2
 2x 15
The Zeros of a Polynomial Function are the
solutions to the equation you get when you
set the polynomial equal to zero.

8. Zeros of a Polynomial Function
The Zeros of a Polynomial
Function ARE the Solutions to
the Polynomial Equation
when the polynomial equals
zero.

9. Graph of a Polynomial Function
Here is the graph of our
polynomial function:
The Zeros of the Polynomial are the values of x
when the polynomial equals zero. In other words,
the Zeros are the x-values where y equals zero.
y  x2
 2x 15

10. y  x2
 2x 15
x-Intercepts of a Polynomial
The points where y = 0 are
called the x-intercepts of the
graph.
The x-intercepts for our graph
are the points...
and
(-5, 0) (3, 0)

11. x-Intercepts of a Polynomial
When the Factors of a Polynomial
Expression are set equal to zero, we get
the Solutions or Roots of the Polynomial
Equation.
The Solutions/Roots of the Polynomial
Equation are the x-coordinates for the
x-Intercepts of the Polynomial Graph!

12. Factors, Roots, Zeros
y  x2
 2x 15
For our Polynomial Function:
The Factors are: (x + 5) & (x - 3)
The Roots/Solutions are: x = -5 and 3
The Zeros are at: (-5, 0) and (3, 0)

13. Factoring a polynomial
means expressing it as
a product of other
polynomials.

14. Factoring polynomials with a
common monomial factor
(using GCF).
**Always look for a GCF before
using any other factoring
method.
Factoring Method #1

15. Steps
1. Find the greatest common factor
(GCF).
2. Divide the polynomial by the GCF.
The quotient is the other factor.
3. Express the polynomial as the
product of the quotient and the GCF.

16. 3 2 2
: 6 12 3
Example c d c d cd
 
3
GCF cd

Step 1:
Step 2: Divide by GCF
(6c3
d 12c2
d2
 3cd)  3cd 
2c2
 4cd  1

17.  3cd(2c2
 4cd  1)
The answer should look like this:
Ex: 6c3
d 12c2
d2
 3cd

18. Factor these on your
own looking for a GCF.
1. 6x
3
 3x
2
 12x
2. 5x2
10x  35
3. 16x3
y4
z 8x2
y2
z3
12xy3
z2
 
2
3 2 4
x x x
  
 
2
5 2 7
x x
  
 
2 2 2 2
4 4 2 3
xy z x y xz yz
  

19. Factoring polynomials that are a
difference of squares.
Factoring Method #2

20. A “Difference of Squares” is a
binomial (*2 terms only*) and
it factors like this:
a2
 b2
 (a  b)(a  b)

21. To factor, express each term as a
square of a monomial then apply
the rule...a2
 b2
 (a  b)(a  b)
Ex: x2
16 
x2
 42

(x  4)(x  4)

22. Here is another
example:
1
49
x2
81 
1
7
x




2
 9
2

1
7
x  9




1
7
x  9





23. Try these on your own:
1. x2
121
2. 9y2
169x2
3. x4
16
Be careful!
  
11 11
x x
  
  
3 13 3 13
y x y x
  
   
2
2 2 4
x x x
   

24. Factoring Method #3
Factoring a trinomial in the
form:
ax2
 bx  c

25. Factoring a
trinomial:
ax2
 bx  c
2. Product of first terms of both binomials
must equal first term of the trinomial.
1. Write two sets of parenthesis, ( )( ).
These will be the factors of the
trinomial.
2
( )
ax

26. 3. The product of last terms of both
binomials must equal last term of the
trinomial (c).
4. Think of the FOIL method of
multiplying binomials, the sum of the
outer and the inner products must
equal the middle term (bx).
Factoring a
trinomial:
ax2
 bx  c

27. x
x
2
: 6 8
Example x x
 
   x x  x2
x
  x
 
Factors of +8: 1 & 8
2 & 4
-1 & -8
-2 & -4
2x + 4x = 6x
1x + 8x = 9x
O + I = bx ?
-2x - 4x = -6x
-1x - 8x = -9x
-2
-4

28. x2
 6x  8
Check your answer by
using FOIL
 (x  2)(x  4)
(x  2)(x  4)  x2
 4x  2x  8
F O I L
 x2
 6x  8

29. Lets do another example:
6x2
12x 18
6(x2
 2x  3) Find a GCF
6(x  3)(x 1) Factor trinomial
Don’t Forget Method #1.
Always check for GCF before you do anything else.

30. When a>1 and c<1, there may
be more combinations to try!
2
: 6 13 5
Example x x
 
2
Find the factors of 6x :
Step 1:
3x  2x
6x  x

31. 2
: 6 13 5
Example x x
 
Find the factors of -5:
Step 2:
5 -1
-5 1
-1 5
1 -5
 
 
 
 
Order can make
a difference!

32. Step 3: Place the factors inside the
parenthesis until O + I = bx.
6x2
 30x  x  5
F O I L
O + I = 30 x - x =
29x
This
doesn’t
work!!
2
: 6 13 5
Example x x
 
6x 1
  x  5
 
Try:

33. 6x2
 6x  5x  5
F O I L
O + I = -6x + 5x = -
x
This
doesn’t
work!!
2
: 6 13 5
Example x x
 
6x  5
  x 1
 
Switch the order of the second terms
and try again.

34. Try another combination:
(3x 1)(2x  5)
6x2
15x 2x 5
F O I L
O+I = 15x - 2x = 13x IT WORKS!!
 (3x 1)(2x  5)
6x2
 13x  5
Switch to 3x and 2x

35. T H E Q U A D R A T I C F O R M U L A
Factoring Technique #4
a
ac
b
b
x
2
4
2





36. Solve using the quadratic formula.
0
2
7
3 2


 x
x
a
ac
b
b
x
2
4
2




2
,
7
,
3 


 c
b
a
)
3
(
2
)
2
)(
3
(
4
)
7
(
)
7
( 2






x
6
24
49
7 


x
6
5
7 

x
6
12

x
6
2

x
3
1
,
2

x
6
25
7 

x

37. Factoring Technique #5
Factoring By Grouping
for polynomials
with 4 or more terms

38. Factoring By Grouping
1. Group the first set of terms and
last set of terms with parentheses.
2. Factor out the GCF from each group
so that both sets of parentheses
contain the same factors.
3. Factor out the GCF again (the GCF
is the factor from step 2).

39. Step 1: Group
3 2
3 4 12
b b b
  
Example 1:
 b3
 3b2
  4b 12
 
Step 2: Factor out GCF from each group
 b2
b  3
  4 b  3
 
Step 3: Factor out GCF
again  b  3
  b2
 4
 

40. 3 2
2 16 8 64
x x x
  
 2 x3
 8x2
 4x 32
 
 2 x3
 8x2
  4x  32
 
 
 2 x2
x  8
  4 x  8
 
 
 2 x 8
  x2
 4
 
 
 2 x 8
  x  2
  x  2
 
 
Example 2:

41. Try these on your own:
1. x
2
 5x  6
2. 3x2
11x  20
3. x3
 216
4. 8x3
 8
5. 3x3
 6x2
 24x

42. Answers:
1. (x  6)(x 1)
2. (3x  4)(x  5)
3. (x  6)(x2
 6x  36)
4. 8(x 1)(x2
 x  1)
5. 3x(x  4)(x  2)