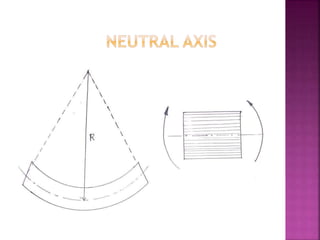
The document discusses the principles of bending stress in beams, focusing on the properties of homogeneous and isotropic materials. It outlines the linear and elastic stress-strain relationship and defines key terms like bending moment, moment of inertia, and section modulus. The relationship between bending stress, distance from the neutral axis, and radius of curvature is also addressed.

1. Lecture Series on
Strength of Materials-6
“Bending Stress”
www.engineersfirst.in

2.  The material of beam is homogeneous and
isotropic.
 Young’s Modulus is the same in tension as in
compression.
 Each layer is free to expand and contract
having no influence in the neighboring layer
for their expansion and contraction.
 The stress-strain relationship is linear and
elastic.
 Sections which are plane before bending
remain plane after bending.
 Beams are initially straight

3.  (M/I= σb /Y=E/R)
 Where σb= Bending Stress
 M = Bending Moment
 I = Moment of Inertia
 E = Modulus of elasticity
 R = Radius of curvature
 y = Distance of the fiber from NA (Neutral
axis)

5.  Section Modulus-It is defined as the ratio of
MI to the distance from the neutral axis.
 It is denoted by “Z”.
 Z=(I/Y)
 Zxx=(Ixx/Y)
 ZYY=(IYY/Y)
 Unit-(mm4/mm)=(mm3)

9. Thank You