Dokumen ini membahas interpolasi spline kubik, yaitu fungsi polinomial berderajat tiga yang menghubungkan titik-titik bersebelahan untuk menghasilkan kurva yang kontinu dan dapat didiferensiasi. Penjelasan meliputi persamaan yang diperlukan dan prosedur untuk menentukan koefisien dalam algoritma interpolasi tersebut. Contoh diberikan untuk menunjukkan penerapan konsep ini dengan titik-titik observasi yang spesifik.

1. Interpolasi Spline
Kubik
Syafrin Muhammad
(03082111005)
Ternate, Kamis 30 November 2023
Disusun Oleh:

2. Pengertian interpolasi spline kubik
Interpolasi spline kubik adalah suatu potongan fungsi polinomial berderajat tiga (kubik)
yang menghubungkan dua titik yang bersebelahan, untuk i = 0, 1, 2, 3, ..., n-1.
Perhatikan gambar berikut:

3. Karena kita ingin spline membentuk garis kontinu dan dapat didiferensiasi, ada satu
set persamaan yang menentukan spline kubik:
Bentuk umum seri polinomial dituliskan pada Persamaan (8.9).
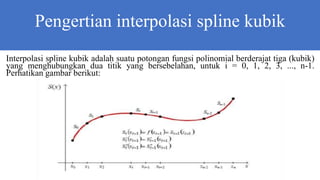
Interpolasi spline
kubik
kita akan mendefinisikan Si sebagai fungsi polinomial kubik
yang mewakili kurva pada domain [xi; xi+1]. Kemudian untuk n
titik observasi, ada n − 1 interpolasi polinomial kubik.
Persamaan (8.10) dan (8.11) sudah cukup jelas. Persamaan (8.12) memastikan bahwa
kita memiliki turunan pertama yang berkelanjutan di setiap simpul internal. Ini
mencegah terbentuknya sudut tajam pada tiap node. Persamaan (8.13) memastikan
turunan kedua juga kontinu, dimana kondisi ini menguntungkan karena itu berarti
turunan pertama itu sendiri dapat didiferensiasi juga. Kondisi ini menyebabkan ada
4n6 kondisi yang harus kita penuhi. Jika 4n4 kita yang tidak diketahui dipecahkan
sebagai sebuah matriks, dan akhirnya matriks tersebut akan terpecahkan, matriks akan
menjadi kurang ditentukan. Kita dapat menyelesaikan kondisi tersebut dengan
memasukkan dua ketentuan tambahan. Dengan splines kubik, secara normal adalah
menentukan akhir di kedua ujung untuk mencapai dua kondisi tambahan. Untuk
contoh ini, dua kondisi yang akan kita tambahkan adalah S′′i (xi) = 0 dan S′′i (xn) = 0.
Kedua kondisi ini memastikan bahwa pada titik akhir, turunan pertamanya linier dan
oleh karena itu fungsi spline berlanjut ke arah yang sudah berjalan. Interpolasi spline
kubik ini disebut juga sebagai “natural spline”.

4. Interpolasi spline kubik
Persamaan (8.12) kita mendapatkan S’i (xi+1) = S′i+1, kemudian S′i+1 −S′i (x) = 0, dan kita dapat mensubstitusi Persamaan
(8.9) ke dalam kedua komponen, pemecahan untuk di dalam hal ini xi, yi, dan ci. Proses yang sama dapat direplikasi dengan
Persamaan (8.13) dan bi. Hasilnya adalah matriks tridiagonal, seperti yang ada pada Chapter 6.3.3, yang dapat dipecahkan
untuk menemukan koefisien. Terdapat sebuah matriks, A, sedemikian rupa sehingga:
Matriks ini sedemikian rupa sehingga:
Kecuali pada u0 = ln. Lebih jauh, diagonal utama D ditentukan menggunakan Persamaan (8.16).
Kecuali pada d0 = dn = 1. Akhirnya vektor V ditentukan dengan Persamaan (8.17).

5. Interpolasi spline kubik
Kecuali pada v0 = vn = 0. Sehingga:
Penyelesaian Persamaan (8.18) akan menghasilkan vektor koefisien c, sehingga koefisien b dapat dihitung menggunakan
Persamaan (8.19).
Dengan menggunakan vektor C yang sudah diketahui, koefisien d dapat dihitung menggunakan Persamaan (8.20).

6. Algoritma
Interpolasi
Spline Kubik
1. Tentukan set titik berpasangan (x, y).
2. Tentukan koefisien ai menggunakan Persamaan (8.10), dimana ai = yi.
3. Hitung elemen diagonal bawah (li) dan elemen diagonal atas (ui) matriks
tridiagonal menggunakan Persamaan (8.15), dimana u0 = ln = 0.
4. Hitung elemen diagonal utama (mi) menggunakan Persamaan (8.16),
dimana d0 = dn = 1.
5. Hitung elemen vektor V menggunakan Persamaan (8.17), dimana v0 = vn
= 0.
6. Susunlah elemen li, ui, dan mi menjadi matriks tridiagonal A.
7. Definisikan persamaan linier seperti pada Persamaan (8.14)
8. Selesaikan sistem persamaan linier pada Persamaan (8.14) sehingga
diperoleh vektor C yang merupakan kumpulan koefisien c.
9. Hitung koefisien bi menggunakan Persamaan (8.19)
10. Hitung koefisien di menggunakan Persamaan (8.20).
11. Bentuk seri persamaan polinomial menggunakan elemen koefisien a, b, c,
dan d yang telah dihitung.
12. Untuk melakukan ekstrapolasi dengan titik observasi diluar rentang titik
diketahui, gunakan persamaan polinomial yang berada pada bagian ujung
terdekat dengan nilai x yang hendak dicari nilai y-nya.

7. Berdasarkan algoritma tersebut, kita dapat menyusun suatu fungsi pada R untuk mencari seri persamaan
polinomial derajat tiga. Fungsi tersebut adalah sebagai berikut:

8. Contoh 8.8
Diketahui koordinat 3 buah titik yaitu (-1,-2), (1,2) dan
(0,1). Jika diketahui titik keempat memiliki koordinat
sumbu x sebesar -2. Tentukan persamaan-persamaan
spline kubik yang dihasilkan dari titik observasi.
Jawaban:
Untuk menentukan persamaan-persamaan linier yang
menghubungkan setiap titik, kita akan menggunakan
fungsi cubic_spline() yang telah kita buat. Berikut adalah
sintaks yang digunakan:
Setelah melakukan pengujian pada Rstudio dengan
mengikuti petunjuk yang tersedia maka cubic spline yang
didapat adalah sebagai berikut:
Jika nilai x dan y diubah dengan sembarang nilai maka
hasil yang di dapat juga berubah dan perubahan nilai
tidak akan berpengaruh terhadap coding yang telah
dimasukan maka cubic spline yang didapat adalah
sebagai berikut:

9. c Thank
You