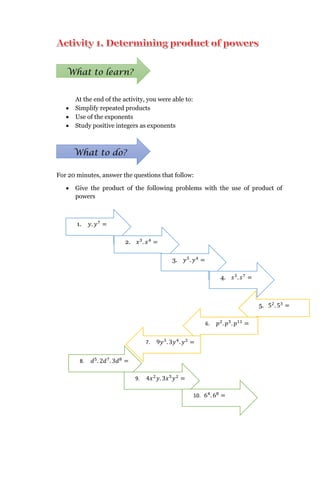
This document provides worksheets and activities to help students learn about integral exponents based on the K to 12 Mathematics curriculum guide. It includes questions and problems for students to practice skills like simplifying expressions with exponents, using properties of exponents, working with zero and negative exponents, and performing operations like multiplication, division, addition and subtraction on terms with exponents. The goal is for students to understand and be able to apply the key concepts of working with integral exponents.

1. INTEGRAL EXPONENT
K to 12 Mathematics Curriculum

2. This module is intended for Grade 8 learners with competency-based
worksheets. Each worksheet has desired outcomes that are based on the learning
competencies in k to 12 curriculum guide in Mathematics specifically on Integral
Exponents. Thus, the following activities in this module will help to fully
understand the procedures in the Integral Exponents.
The learner demonstrates understanding of key concepts of Integral
Exponents, solving power of a product, power of a power and quotient of a
power of integral exponents.
The learner is able to investigate thoroughly mathematical
relationships in various situations, using the integral exponents and
understand the properties of fundamental operation use in Integral
expponents.
The learner …
Solve an integral exponents….
By product of a power
By power of a power
By power of a product
By quotient of a power
Module 2
Content Standard
Performance Standard
Learning competencies

3. At the end of the activity, you were able to:
 Simplify repeated products
 Use of the exponents
 Study positive integers as exponents
For 20 minutes, answer the questions that follow:
 Give the product of the following problems with the use of product of
powers
What to do?
What to learn?
1. 𝑦. 𝑦7
=
2. 𝑥3
. 𝑥4
=
3. 𝑦5
. 𝑦4
=
5. 52
. 53
=
6. 𝑝2
. 𝑝5
. 𝑝11
=
7. 9𝑦3
. 3𝑦4
. 𝑦2
=
8. 𝑑5
. 2𝑑7
. 3𝑑8
=
9. 4𝑥2
𝑦. 3𝑥5
𝑦2
=
10. 64
. 68
=
4. 𝑠3
. 𝑠7
=

4. At the end of the activity, you will be able to:
 Solve the equation by multiplying exponents
 Discuss the process of multiplication in solving exponents
For 10 minutes, discuss and simplify the following. Answer the questions that
follow.
What to learn?
What to do?
1. (𝑥2)3
=
3. (𝑟4)5
=
2. (𝑦6)8
=
4. (𝑘4)10
=
5. (𝑏3)7
=
7. (𝑗6)1
=
6. (𝑧7)3
=
9. (𝑦6)8
=
8. (𝑚6)5
=
10. (𝑚6)5
=

5. At the end of the activity, you will be able to:
 Learn how commutative and associative property of multiplication
 Learn what is power or a monomial
For 15 minutes, simplify the following problems:
 Using power of products to solve integers
 Solve the problems using power of monomials
At the end of the activity, you will be able to:
 Determine what the quotient of the power is and what are the properties
used.
 Learn how and when to use the quotient of powers.
What to learn?
What to do?
1. (34
𝑦2)52
2. (2𝑤2)2
3. (𝑧3
𝑤2)4
4. (𝑚3
𝑛2)5
5. (5𝑎2)3
6. (4𝑝2
𝑞2)5
7. (𝑥3
𝑦2)25
8. (6𝑥3
𝑦4)4
What to learn?

6. For 20 minutes, simplify the following problems:
 Find the difference of the exponents using quotients of the powers
 Assume all denominators are not equal to zero.
At the end of this activity, you will be able to:
 Solve fraction with positive integer exponents
 Learn how to use power of fraction in solving problems
For 10 minutes, answer the following question using power of fraction.
What to do?
1. 75
÷ 73
= 2. 106
÷ 103
= 3. 𝑎10
÷ 𝑎4
=
8.
45𝑎6 𝑏4
𝑎3 𝑏
=
5. 𝑥6
÷ 𝑥23
=
7.
𝑚6 𝑚4
𝑚𝑛
=
75
÷ 73
=
6. 𝑚3
÷ 𝑚2
=4. 𝑏3
÷ 𝑏43
=
9.
15𝑥3 𝑦3
3𝑥2 𝑦
=
What to learn?
What to do?
1. (
𝑥
𝑦
)
3
= 5. (
2
𝑐2)
2
= 7. (
𝑟𝑔
𝑠
)
8
=

7. At the end of this activity, you will be able to:
 Determine the exact value of a number when the exponent is zero.
 Learn how to use zero and negative exponents in solving problems
For 15 minutes, answers the following questions given below.
 Simplify the following equations.
What to learn?
What to do?
2. (
2
3
)
2
=
.
3. (
3𝑥2
4𝑦3
)
3
=
.
4. (
𝑏
ℎ
)
3
=
6. (
𝑟𝑞
𝑑𝑠
)
5
=
8. (
𝑎𝑠2
𝑓𝑑3
)
5
=
9. (
𝑙
𝑑
)
6
=
1. (𝑎2
𝑏3)0
=
2. (𝑥2
𝑦𝑧3)0
=
3. (2𝑝2
𝑞3)0
=
4. (3𝑠2
𝑠4)0
=
5. (6𝑚2
𝑛3)0
=
6. (4𝑥2
𝑦3
𝑧4)−1
=
7. (6𝑚3
𝑛2
𝑞4)−3
1.
8. (15𝑎6
𝑏3
𝑐8)−2
9. (10𝑑3
𝑒3
𝑓3)−2
10. (𝑎7
𝑏0
𝑐3)−5

8. At the end of this activity, you will be able to:
 Solve problems using rewriting algebraic expressions with zero and
negative exponents
For 20 minutes, answer the following problems using rewriting algebraic
expressions with zero and negative exponents.
At the end of this activity, you will be able to:
 Learn the deferent expressions that said to be in simplest form, and;
 Learn how to use it in solving problems.
What to learn?
What to do?
What to learn?
1. 𝑎−3
=
2. 3𝑥0
=
3. 𝑚5
𝑛0
=
4. (4𝑎2)0
=
5. 2𝑚−1
=
6. (𝑥𝑦)−3
=
7. (2𝑎)−3
=
8. −5𝑦−2
=
9.
𝑎−3
𝑏
=
10.
𝑥−5
𝑦−3
=

9. For 20 minutes, answer the following equation using simplifying exponential
expressions.
 Simplify each expression. Assume all denominators are not equal to
zero.
At the end of the activity, you will be able to:
 Divide integer exponents
 Apply concepts and laws of exponents
For 15 minutes, solve and answer the following problems.
 Perform and simplify the indicated operation.
What to do?
1. 30
. 33
2. (2𝑎2
− 𝑏−2)−3
3. 24
. 2−1
4. (18𝑎2
𝑏−2
− 7𝑎3
𝑏−5)0
5. 3𝑐−1
𝑑−1
(2𝑐𝑑 − 7𝑐2
𝑑2
)
What to learn?
What to do?
2. (2−1
+ 1)2
=
1.
3𝑠2 𝑡2 −2
𝑠2
=
4.
6𝑠5 𝑦−2 4
𝑠2 =
3.
6𝑑𝑓𝑔5 𝑦𝑠𝑔ℎ−8 0
𝑠2
=
6. ( 𝑑0
𝑟1)9
5. ( 𝑔−3
𝑎−5
−2𝑘2)3
=